EXPERIMENTAL STUDY AND DESIGN METHOD ON MECHANICAL BEHAVIOR OF PARTIALLY PRECAST PRESTRESSED STEEL REINFORCED CONCRETE BEAMS
-
摘要:
为简化现场施工工序,创新将预应力技术与装配式技术集成应用于型钢混凝土结构中,提出部分预制预应力型钢混凝土(PPPSRC)梁。通过5个梁试件的受弯性能试验及5个梁试件的受剪性能试验,研究了预应力施加顺序、预应力度、预应力筋高度及预制混凝土种类对PPPSRC梁的破坏形态和截面应力发展的影响,并结合试验结果对各试件的裂缝发展规律、承载及变形能力进行了分析研究。研究结果表明:预应力施加于梁预制部分或施加于整个梁对PPPSRC梁受力性能影响较小,不同预应力施加顺序的试件开裂荷载与峰值荷载差值均在5%以内;预应力度和预制部分混凝土种类对PPPSRC梁的抗裂性能影响显著,其中PPPSRC梁的开裂荷载相较于普通型钢混凝土梁最高可提高166%,而预制部分采用超高性能混凝土相比预制部分采用普通混凝土的试件开裂荷载可提高33%。基于试验结果建立了适用于PPPSRC梁的受弯、受剪承载力以及开裂荷载的计算公式,计算结果与试验结果吻合较好。
Abstract:To simplify the on-site construction procedure of steel reinforced concrete (SRC) beams, this paper combined the advantages of pre-stressing technique and prefabricated structures, and then presented a novel partially precast prestressed steel reinforced concrete beams. Based on the test results of 5 flexure-dominant beams and 5 shear-dominant beams, the effects of pre-stressing timing, pre-stress ratio, pre-stress location, and the type of precast concrete on failure pattern and strain distribution were investigated. Meanwhile, the crack propagation, load-carrying capacity and deformation development of PPPSRC beams were thoroughly explored. The test results indicate that the pre-stressing timing has a limited effect on the mechanical behavior of PPPSRC beams because the cracking load difference and the peak load difference of different pre-stressing timings were both within 5%. The pre-stress ratio and location strongly affect the anti-cracking capacity of PPPSRC beams. The cracking load can be increased by 166% and 33% when higher pre-stress ratio and UHPC are applied, respectively. Equations for predicting the flexural strengths, shear strengths and cracking loads of PPPSRC beams were put forward, and the calculated values are in good agreement with the test results.
-
型钢混凝土结构(steel reinforced concrete structure,简称 SRC 结构)作为钢-混组合结构的一种重要形式,具有承载力高、延性好等特点,被广泛应用于各项大跨、重载结构的建设中[1] 。然而随着跨度的增加,正常使用极限状态下的挠度及裂缝计算往往起控制作用,内置型钢虽然能够限制裂缝间距,但无法有效地控制裂缝宽度。
为此,国内外学者对预应力型钢混凝土结构(prestressed steel reinforced concrete structure,简称PSRC结构)进行了大量的试验研究。其中,傅传国等[2]、李峰等[3]以及王钧等[4]进行了预应力型钢混凝土梁和普通型钢混凝土梁的受弯性能试验研究,分析了其受力过程、破坏形态、裂缝开展与分布规律、刚度变化规律等,结果表明:预应力型钢混凝土梁比普通型钢混凝土梁具有更好的刚度和抗裂性能。贾金青、孟刚等[5-7]对预应力型钢超高强混凝土梁的受弯、受剪性能以及延性进行了研究,结果表明:① 超高强混凝土脆性破坏显著,导致预应力型钢超高强混凝土梁极限状态后承载力骤降,但内置型钢有效提高了极限荷载后的持荷能力,试验梁仍具有较好的延性;② 预应力型钢超高强混凝土梁和预应力型钢普通强度混凝土梁的裂缝形态和荷载-挠度曲线特征基本相同。但预应力型钢超高强混凝土梁具有更好的受剪承载力、剪切延性以及更大的刚度。熊学玉、高峰等[8-9]进行了单调及反复竖向荷载作用下无黏结预应力型钢混凝土框架的试验研究,结果表明:预应力型钢混凝土框架的滞回曲线呈“梭形”,且较丰满,刚度退化低于预应力混凝土框架结构,试件表现出良好的抗震性能和变形能力。目前,PSRC结构主要应用在一些大型超高层建筑和大跨结构中,如我国山东省世贸中心底部转换梁、南京金山大厦转换层、山东体育学院综合训练馆以及钱塘江四桥等。然而由于预应力现场施工过程复杂,且常常存在质量缺陷(张拉时间、张拉控制、管道堵塞),施工质量往往无法满足设计要求。因此本文参考相关文献[10-18],将预制装配技术与PSRC结构相结合,同时考虑到运输吊装的轻便性,提出部分预制预应力型钢混凝土梁(partially precast prestressed steel reinforced concrete beam,简称PPPSRC梁)。其制作过程可分为2部分完成,首先在工厂预制内含型钢及钢筋骨架的U形外壳,然后在施工现场对U形外壳进行安装并浇筑U形槽及楼板混凝土。为保证预制部分和现浇部分组合良好,在预制部分的U形槽内间隔设置一定数量的混凝土横隔板,以此来抵抗新、旧混凝土之间的界面剪力。
PPPSRC梁相比全预制型钢混凝土梁运输吊装更加方便,相比现浇型钢混凝土梁更容易保证施工质量,且能通过差异化使用材料来进行截面优化以获得不同的受力性能。但对于预应力型钢混凝土梁而言,部分预制构件的受力性能是否可以等同现浇,目前尚无学者研究。
1 试验概况
1.1 试验设计
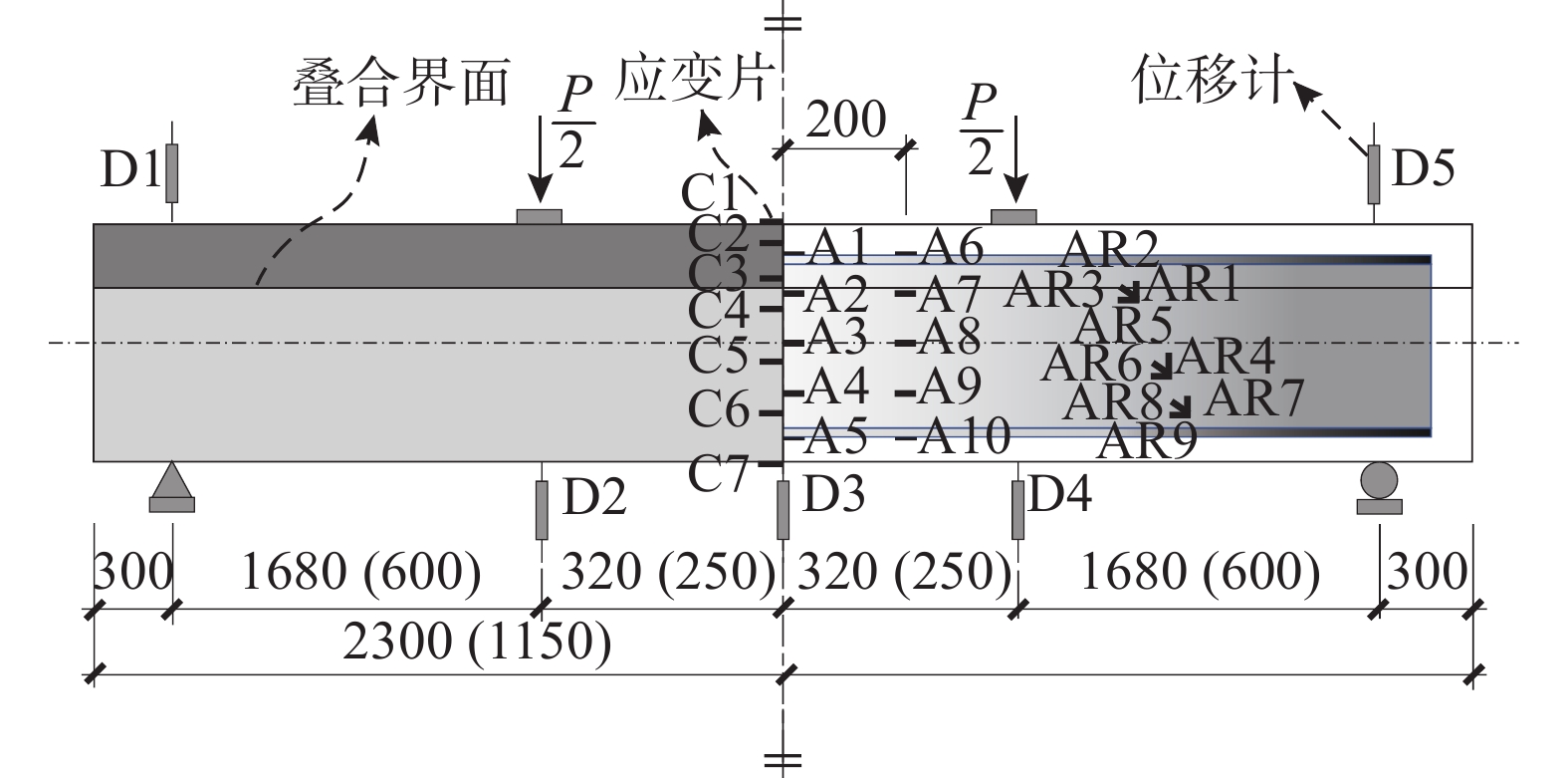
如表1所示,试验共设计10个试件,包括8个PPPSRC试件和2个PPSRC试件。其中5个受弯试件的长度为4600 mm,用于研究不同预应力度、预应力施加顺序以及预制混凝土类型下梁的受弯性能;5个受剪试件的长度为2300 mm,用于研究不同预应力度、预应力施加顺序以及预应力筋高度下梁的受剪性能。如图1所示,所有试件均为叠合梁,截面尺寸为300 mm×650 mm,其中预制部分采用高强混凝土以提升施工期强度与刚度,现浇部分采用普通强度混凝土以降低结构造价。试验采用直径15.2 mm的1860级高效低松弛钢绞线,通过后张法无粘结工艺施工。受弯试验中,纵筋采用4根直径20 mm的HRB335级钢筋,箍筋采用直径8 mm 的HPB300级钢筋,间距80 mm,型钢采用Q235B级热轧H型钢,型号为HN496 mm×199 mm×9 mm×14 mm。受剪试验中,上部纵筋为2根直径25 mm的HRB400级钢筋,下部纵筋为4根直径32 mm的PSB1080精轧螺纹钢,箍筋采用直径6 mm 的HPB300级钢筋,间距150 mm,型钢亦采用Q235B级热轧H型钢,型号为HN500 mm×200 mm×10 mm×16 mm。
表 1 试件设计主要参数及结果Table 1. Main parameters and results of specimen design研究内容 试件编号 预制/现浇混
凝土强度等级张拉控
制应力预应力度 预应力
布筋形式预应力
施加顺序预应力筋 预应力
施加高度预制/现浇混
凝土强度fcu/MPa开裂荷载
Pcr/kN极限荷载
Pu/kN受弯性能 PPSRC-1-1 C60/C50 − 0.00 − − − − 77.1/50.8 109 1182 PPPSRC-1-2 C60/C50 0.15fptk 0.06 直线型 A 2× 
− 61.5/52.9 140 1366 PPPSRC-1-3 C60/C50 0.40fptk 0.29 直线型 A 4× 
− 69.4/54.3 290 1397 PPPSRC-1-4 C60/C50 0.40fptk 0.29 直线型 B 4× 
− 66.7/60.4 276 1463 PPPSRC-1-5 C110/C50 0.40fptk 0.15 直线型 A 2× 
− 116.3/60.0 385 1486 受剪性能 PPSRC-2-1 C70/C40 − 0.00 − − − − 72.8/46.0 440 4017 PPPSRC-2-2 C70/C40 0.30fptk 0.06 直线型 A 4× 
C 72.8/46.0 620 4010 PPPSRC-2-3 C70/C40 0.60fptk 0.12 直线型 A 4× 
C 72.8/46.0 1220 4210 PPPSRC-2-4 C70/C40 0.30fptk 0.06 直线型 B 4× 
C 72.8/46.0 805 4352 PPPSRC-2-5 C70/C40 0.30fptk 0.06 直线型 B 4× 
D 72.8/46.0 795 3911 注:试件预应力施加顺序分为A、B两类,其中A类试件为预应力施加在预制梁上,B类试件为预应力施加在整梁上;试件的预应力施加高度分为C、D两类,其中C类试件预应力合力作用点距梁底104 mm,D类试件预应力合力作用点距梁底230 mm;fptk为预应力筋的极限强度标准值;fcu为立方体抗压强度平均值。 1.2 材料性能
本试验中计算所用材料参数均采用试验值,其中混凝土力学性能见表1,钢材力学性能见表2。表3为本试验所用C110级超高性能混凝土配合比。
表 2 钢材力学性能Table 2. Mechanical properties of steel种类 直径或
厚度/mm屈服强度
fy/MPa极限强度
fu/ MPa弹性模量
Es/ MPa钢筋及预应力筋 6 432 624 2.10×105 8 354 537 2.10×105 20 427 612 2.00×105 25 430 625 2.10×105 32(精轧螺纹钢) 1103 1211 2.07×105 15.2(钢绞线) 1659 1952 1.95×105 型钢(Q235) 9 353 480 2.05×105 10 353 480 2.05×105 14 304 465 2.05×105 16 304 465 2.05×105 表 3 C110混凝土配合比设计Table 3. Mix design of C110-grade concrete质量比 钢纤维
体积掺量/(%)水泥 粉煤灰 矿粉 硅灰 砂 水 减水剂 1.00 0.25 0.08 0.08 1.34 0.28 0.03 2.5 1.3 施工流程
本试验提出的PPPSRC梁施工流程如图2所示,步骤共分为预制和现浇两部分完成,其中预制过程包括钢筋绑扎、模板安装、预制混凝土浇筑以及预应力筋张拉,现浇过程包括预制梁的安装及现浇混凝土浇筑。在钢筋绑扎的过程中,型钢腹板两侧粘贴泡沫板作为内模可用于混凝土横隔板的预制,当预制混凝土浇筑完成并达到一定强度后张拉预应力筋,最后用松香水对泡沫板进行溶解以形成U形槽。
1.4 加载装置及加载方案
试验采用200 00 kN四立柱式电液伺服压力试验机进行加载,位移计及应变片的布置如图3所示,跨中位移计分别位于加载点及对称轴正下方,支座位移计位于支座正上方。试验过程中试件荷载由电液伺服压力试验机测控系统自动实时采集,主要监测试件的竖向荷载、挠度以及混凝土和型钢的应变。
2 受弯试验结果及分析
2.1 破坏形态
如图4所示,从试验梁破坏时的裂缝形态可以看出,所有试件均呈现典型的弯曲破坏模式。试件加载过程中,预制与现浇部分混凝土之间未出现粘结裂缝,型钢翼缘与混凝土界面亦无水平裂缝出现,说明各部分共同工作性能良好。试验中所有试件均表现出相似的裂缝发展过程,主要差别在于:试件 PPSRC-1-1由于未施加预应力,开裂荷载仅为极限荷载的9.2%;试件PPPSRC-1-3施加预应力,开裂荷载为极限荷载的19.5%;试件PPPSRC-1-5预制部分采用超高性能混凝土,开裂荷载为极限荷载的25.9%。加载过程中,PPPSRC梁的裂缝宽度及开展高度要小于部分预制型钢混凝土梁(PPSRC-1-1),当荷载达到60%极限荷载时,试件PPSRC-1-1与PPPSRC-1-3裂缝宽度分别为0.273 mm与0.170 mm。由此可见,预应力不仅可以大幅提高开裂荷载,而且可以有效抑制裂缝宽度。
2.2 荷载-挠度曲线
受弯试件的荷载-挠度曲线如图5所示,加载初期曲线斜率并无明显差别,初始刚度基本相同;加载中期,曲线逐渐分离;当试件达到峰值荷载后,曲线未出现明显下降,承载能力仍然保持在较高水平。这是由于,受压区混凝土压碎后,型钢和箍筋与约束的核心区混凝土形成“芯”梁,当受压区混凝土压碎后,伴随着型钢翼缘的强化,截面发生了内力重分布,因此承载力在峰值荷载后仍保持在较高水平。
2.3 混凝土、型钢沿截面高度的应变分布情况
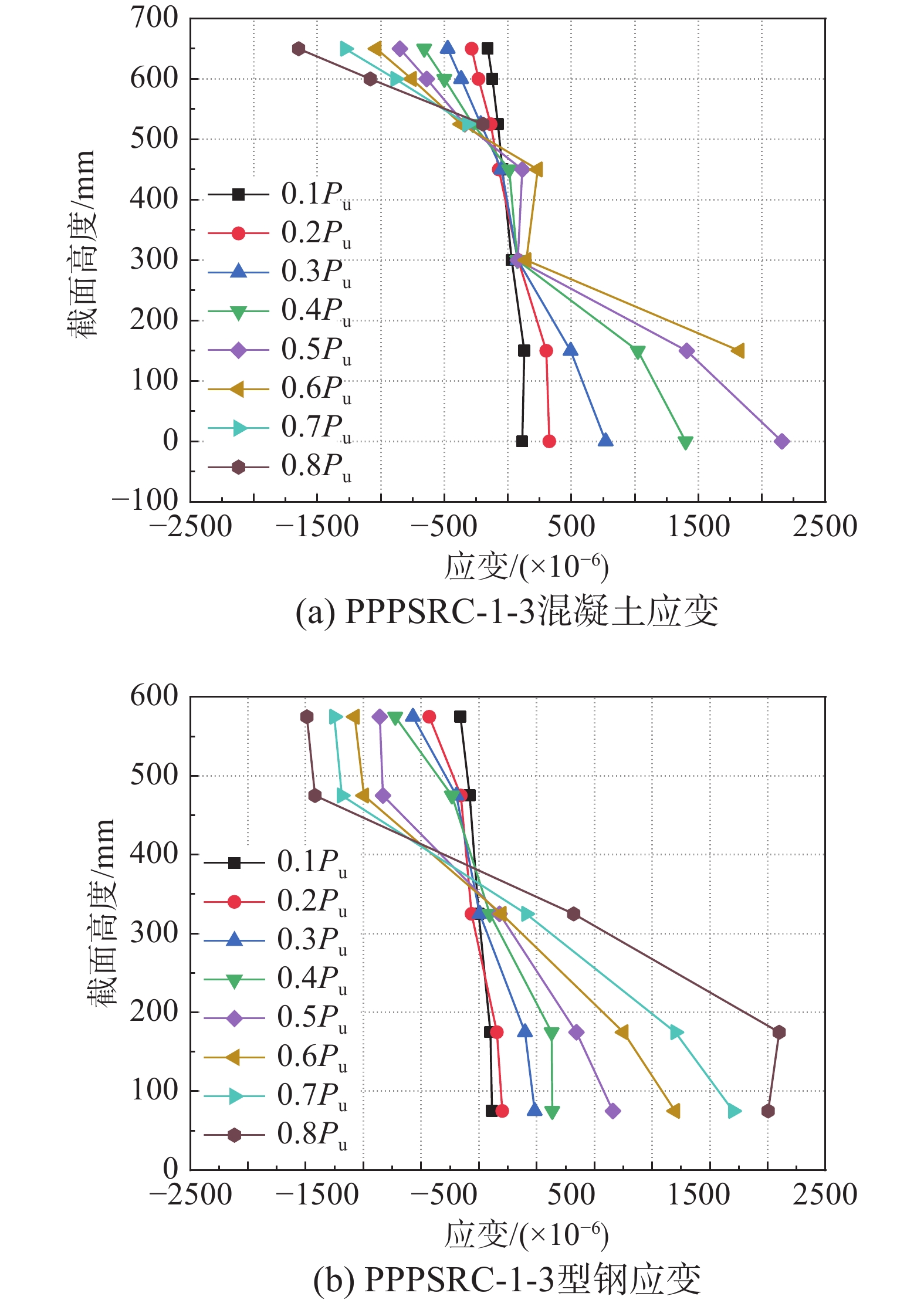
图6分别给出了部分试件跨中处混凝土和型钢在不同受力阶段沿截面高度的应变分布情况。可以看出:试验梁开裂前,同一截面应变具有较好的线性关系;开裂后,由于型钢和混凝土之间的粘结滑移产生了应力重分布,同一截面应变不再满足线性关系。型钢由于其匀质性,在弯曲应力作用下其应变分布沿截面高度应呈直线,但由于试件制作及应变测点布置时存在一定施工误差,在大应力作用下型钢应变出现个别跳点。
2.4 受弯性能的影响因素分析
2.4.1 预应力施加顺序
除预应力施加顺序外,试件PPPSRC-1-3和试件PPPSRC-1-4的设计参数基本相同。其中试件PPPSRC-1-3预应力施加在预制部分,试件PPPSRC-1-4预应力施加在整个梁上。从试验结果可以看出,试件PPPSRC-1-3与试件PPPSRC-1-4的开裂荷载与峰值荷载差值均在5%以内。相比PPSRC-1-1,预应力对开裂荷载及峰值荷载的提升作用显著,其中开裂荷载分别提高了约166%和153%,峰值荷载分别提高了约18%和24%。由此可以得出,在预制部分施加预应力能够达到与全截面施加预应力相同的效果,预应力对型钢混凝土梁的受力性能提升作用显著。
2.4.2 预应力度
试件PPSRC-1-1、PPPSRC-1-2、PPPSRC-1-3的预应力度分别为0.00、0.08、0.29,开裂荷载分别为109 kN、140 kN、290 kN,极限荷载分别为1182 kN、1366 kN、1397 kN。当预应力度从0.00增加到0.08,开裂荷载提高28.4%,峰值荷载提高15.6%;当预应力度从0.08提升至0.29,开裂荷载提高107.1%,峰值荷载提高2.3%。这是由于峰值荷载主要受配筋率影响,预应力度从0.00到0.08,截面中增加了预应力筋,因此峰值荷载明显提高,而预应力度从0.08到0.29,截面配筋并无变化,峰值荷载无明显提升。由此可以得出,预应力对开裂荷载提升作用显著,但较低的预应力度对开裂荷载的提升幅度不如高预应力度明显。
2.4.3 混凝土类型
试件PPPSRC-1-5的预制部分采用C110超高性能混凝土,实测混凝土强度为116.3 MPa,试件PPPSRC-1-3的预制部分采用C60高强混凝土,实测混凝土强度为69.4 MPa。尽管试件PPPSRC-1-5的预应力度小于试件PPPSRC-1-3,分别为0.15和0.29,但相比试件PPPSRC-1-3,试件PPPSRC-1-5的开裂荷载提高了32.8%,极限荷载提高了6.4%。由此可以看出,预制部分采用超高性能混凝土对PPPSRC梁的抗裂性能具有明显的提升作用,且能够达到优化截面、提升承载力的作用。
3 受剪试验结果及分析
3.1 破坏形态
如图7所示,所有试件均呈现剪压破坏模式。试验过程中,预制和现浇混凝土之间未发现粘结裂缝,二者协同工作性能良好。以试件PPPSRC-2-3为例,加载初期,试件处于弹性工作状态;当荷载达到29%Pu时,首先在跨中纯弯段出现细微的竖向裂缝;随着荷载的不断增加,剪跨段出现一系列弯剪斜裂缝并指向加载点;加载至95%Pu时,加载点下混凝土轻微起皮剥落,剪跨段斜裂缝向跨中斜向延伸,并在跨中位置相交形成拱形;临近极限荷载时,剪跨段斜裂缝宽度不断增大,加载点下方混凝土压碎,构件破坏。
3.2 荷载-挠度曲线
由图8可知,所有试件的初始刚度无明显区别,承载力水平相差较小;由于型钢的存在,达到峰值荷载后,荷载-挠度曲线未出现明显的下降。其破坏形态明显区别于钢筋混凝土梁的脆性破坏,表现出良好的延性。
3.3 受剪性能的影响因素分析
3.3.1 预应力施加顺序
由表1可知,试件PPPSRC-2-2的预应力施加在预制部分,而试件PPPSRC-2-4的预应力施加在整个梁上。从试验结果可以看出,试件PPPSRC-2-4的跨中开裂荷载比试件PPPSRC-2-2提高了29.8%,峰值荷载提高了8.5%。虽然试件PPPSRC-2-4的跨中开裂荷载较高,但两个试件的峰值荷载基本相同。考虑到剪切承载力是衡量剪切性能的最主要因素,因此可以认为预应力施加顺序对PPPSRC梁的受剪性能影响较小。
3.3.2 预应力度
试件PPSRC-2-1、PPPSRC-2-2、PPPSRC-2-3的预应力度分别为0.00、0.06、0.12,跨中开裂荷载分别为440 kN、620 kN、1220 kN,极限荷载分别为4017 kN、4010 kN、4210 kN。从试验结果可以看出,预应力对跨中开裂荷载的提高效果显著,而对承载力的影响较小。此外,当试件达到正常使用极限状态(60%极限荷载)时,试件PPSRC-2-1、PPPSRC-2-2、PPPSRC-2-3的跨中裂缝宽度分别为0.67 mm、0.56 mm、0.30 mm。由此可见,预应力不仅可以大幅提高跨中开裂荷载,而且可以有效抑制跨中裂缝宽度。
3.3.3 预应力筋高度
试件PPPSRC-2-4和试件PPPSRC-2-5的预应力筋分别布置在距梁底104 mm和230 mm高度处,开裂荷载分别为805 kN和795 kN,峰值荷载分别为4352 kN和3911 kN。从试验结果可以看出,预应力筋高度对开裂荷载影响较小,但对峰值荷载的影响较为明显。相比预应力筋高度为230 mm的试件,预应力筋高度104 mm的试件峰值荷载提高了11.3%。
4 承载力计算方法
4.1 受弯承载力计算方法
试验过程中未发现型钢与混凝土间出现粘结滑移裂缝,因此可认为型钢与混凝土组合良好。参考现行组合结构设计规范[19],本文提出PPPSRC梁受弯承载力计算公式。
基本假定如下:① 截面应变发展符合平截面假定;② 受压区混凝土极限压应变取0.003;③ 不考虑普通混凝土的抗拉强度,考虑UHPC受拉强度并予以25%的折减[20],有效受拉区混凝土面积取为矩形;④ 型钢全截面与纵向受拉钢筋在承载力极限状态时均已达到屈服强度。
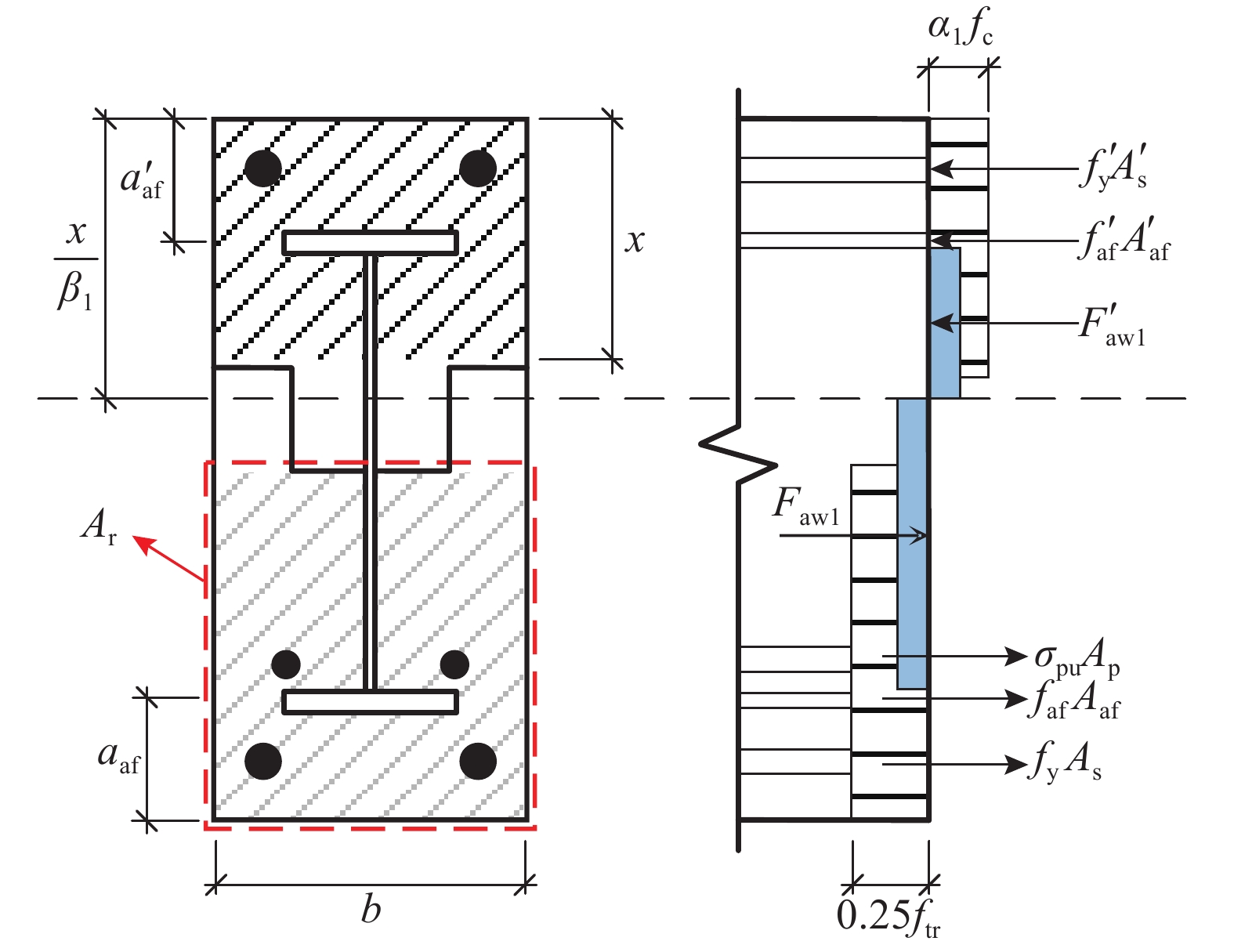
由截面分析可知,截面中和轴处于不同位置时应采用不同的设计公式计算PPPSRC梁的受弯承载力。本文中所有试件达到承载力极限状态时中和轴均位于型钢腹板,因此以中和轴通过型钢腹板为例说明计算流程,计算简图见图9。图中:
F′w1=f′awtw(xβ1−a′af−tf2), Fw1=fawtw(h−aaf−tf2−xβ1)。 受弯承载力可由式(1)、式(2)进行计算:
α1fcbx+f′yA′s+f′afA′af=fyAs+σpuAp+fafAaf+fawtw(h−2xβ1)+0.25ftrAr (1) Mu=α1fcbx(xβ1−x2)+f′sA′s(xβ1−a′s)+f′afA′af(xβ1−a′af)+12f′awtw(xβ1−a′af−tf2)2+12fawtw(h−aaf−tf2−xβ1)2+σpuAp(hp−xβ1)+0.25ftrAr(hr−xβ1) (2) 式中:α1和β1根据混凝土结构设计规范[21]进行计算;x为矩形应力图的受压区高度;a′s为受压钢筋中心到混凝土受压区边缘的距离;a′af为型钢受压翼缘中心到混凝土受压区边缘的距离;aaf为型钢受拉翼缘中心到混凝土受压区边缘的距离;tf为型钢翼缘厚度;tw为型钢腹板厚度;h′a为型钢腹板正好受压屈服高度处至混凝土受压区上边缘的距离;ha为型钢腹板正好受拉屈服处至混凝土受压区上边缘的距离;h0f为型钢下翼缘截面重心至混凝土受压区上边缘的距离;h0s为非预应力受拉钢筋的合力点到受压区混凝土上边缘的距离; hp为无粘结预应力受拉钢筋的合力点到受压区混凝土上边缘的距离;hr为考虑UHPC受拉区中心到受压区混凝土边缘的距离;Ar为UHPC受拉区面积; Ap为无粘结预应力筋总截面面积;Aaf为型钢下翼缘截面面积;Aaw为型钢腹板截面面积;A′af为型钢上翼缘截面面积;fc为换算混凝土抗压强度,按照式(10)进行计算;f′af为型钢受压翼缘屈服强度; faf为型钢受拉翼缘屈服强度;faw为型钢腹板受拉屈服强度;σaf为型钢上翼缘中心处拉应力;σ′af为型钢上翼缘中心处压应力;σpu为预应力筋的极限应力;ftr为UHPC受拉强度。
上述计算方法计算出的试验梁正截面受弯承载力及试验实测的受弯承载力结果如表4所示。通过比较分析可以发现,本文所提出的受弯承载力计算方法的计算值与试验值吻合较好且偏于安全,可用于PPPSRC梁受弯承载力的设计计算。
表 4 受弯承载力试验值与计算值对比Table 4. Comparison between tested and calculated values of flexural capacity试件编号 试验
峰值
荷载
Ptu/kN受弯
承载力
试验值
Mtu/(kN·m)受弯
承载力
计算值
Mcu/(kN·m)Mcu/Mtu 平均值 变异
系数PPSRC-1-1 1182.2 993.05 945.75 0.95 0.94 0.04 PPPSRC-1-2 1366.0 1147.44 1029.19 0.90 PPPSRC-1-3 1397.4 1173.82 1171.25 1.00 PPPSRC-1-4 1463.0 1228.92 1184.28 0.96 PPPSRC-1-7 1486.6 1248.74 1134.45 0.91 4.2 受剪承载力计算方法
基于试件破坏形态与试验结果,本文将PPPSRC梁的受剪承载力分为三部分考虑,即:混凝土、型钢以及预应力筋对受剪承载力的贡献。PPPSRC梁的受剪承载力计算公式如式(3)所示:
V⩽ (3) 式中,Vc、Va、Vp分别为混凝土、型钢及预应力筋提供的受剪承载力。
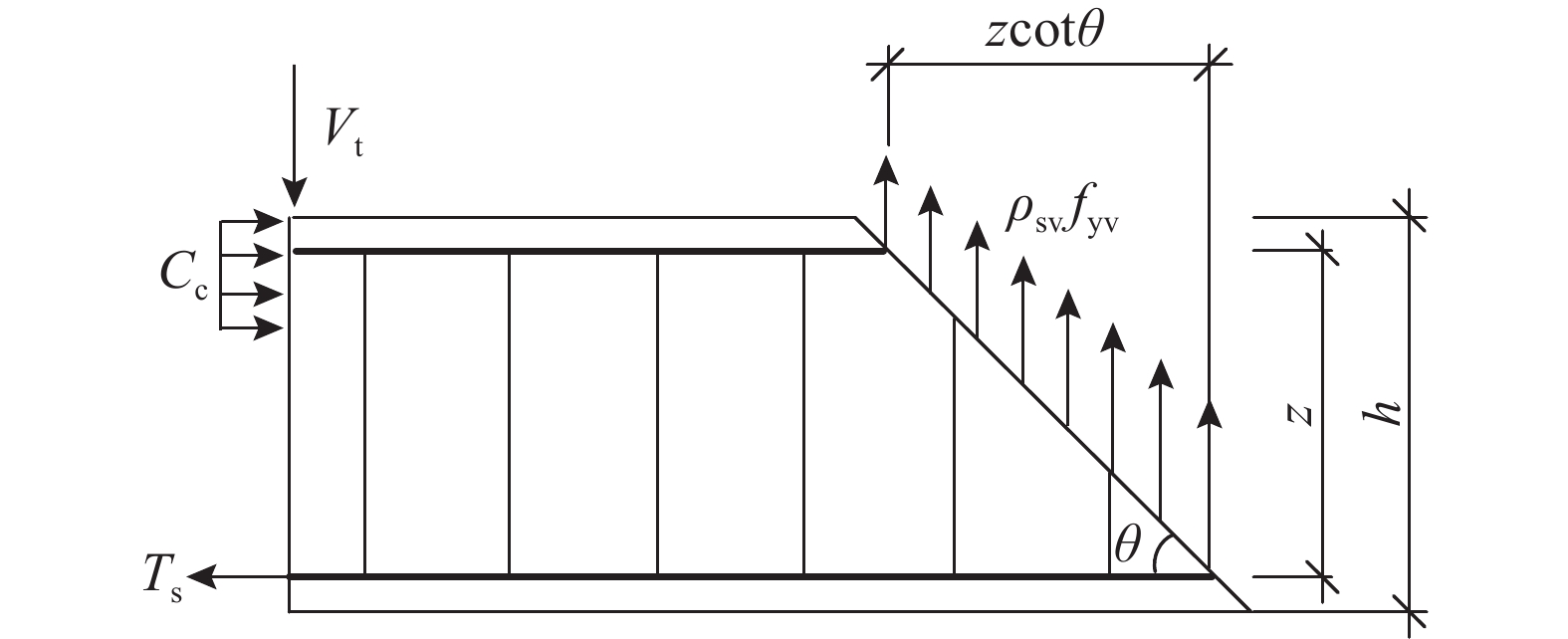
混凝土的受剪承载力使用传统模型计算。“桁架-拱”模型是在桁架模型的基础上,考虑混凝土拱体效应发展而来的模型,其计算简图如图10、图11所示[22]。
{V_{\text{c}}}={V_{\text{t}}} + {V_{\rm a}} (4) {V_{\text{t}}} = {f_{{\text{yv}}}}{\rho _{{\text{sv}}}}b{\textit{z}}\cot \theta (5) {V_{\text{a}}} = b{c_{\text{a}}}\left( {0.85v{f_{\text{c}}}-\frac{{{\rho _{{\text{sv}}}}{f_{{\text{yv}}}}}}{{{{\sin }^2}\theta }}} \right)\tan \alpha (6) 式中:Vt为桁架模型提供的受剪承载力;Va为拱模型提供的受剪承载力;fyv为箍筋的屈服强度;ρsv为箍筋配箍率;z为纵筋间距;v为混凝土的软化系数,本文中取v = 0.7−fc / 200 [23];ca为剪压区混凝土截面高度,采用式(7)进行计算。
{c_{\text{a}}} = {\left[ \sqrt{{{(n{\rho _{{\text{se}}}})}^2} + 2n{\rho _{{\text{se}}}}} - n{\rho _{{\text{se}}}}\right]} \cdot h (7) 式中:ρse为受拉纵筋配筋率;n为型钢刚度与混凝土刚度的比值;h为梁截面高度。
依据《钢骨混凝土结构设计规程》(YB 9082−2006)[24],型钢的受剪承载力采用简化的畸变能强度理论确定,如式(8)所示:
{V_{\text{a}}} = 0.6{f_{{\text{aw}}}}{t_{\text{w}}}{h_{\text{w}}} (8) 预应力筋对PPPSRC梁受剪承载力贡献的机理与预应力混凝土构件类似,因此参照现行《预应力混凝土结构设计规范》(JGJ 369−2016)[25]加以考虑:
{V_{\text{p}}} = 0.05{N_{\text{p}}} (9) 考虑到PPPSRC梁截面中存在两种不同强度的混凝土,本文采用面积加权得到换算混凝土的强度:
{f_{\rm c}} = \frac{{{A_1}}}{{{A_1} + {A_2}} }{f_{{\text{c1}}}} + \frac{{{A_2}}}{{ {{A_1} + {A_2}} }}{f_{{\text{c2}}}} (10) 式中:A1为预制部分截面面积;A2为现浇部分截面面积;fc1为预制部分混凝土抗压强度;fc2为现浇部分混凝土抗压强度。
按照上述方法计算出的受剪承载力见表5。从计算结果可以看出,计算值与试验值吻合较好且偏于安全,可用于PPPSRC梁受剪承载力的设计计算。
表 5 受剪承载试验值与计算值Table 5. Comparison between tested and calculated values of shear strength试件编号 Vb/kN Vt/kN Vb/Vt 平均值 变异系数 PPSRC-2-1 1814.17 2008 0.90 0.89 0.04 PPPSRC-2-2 1829.79 2005 0.92 PPPSRC-2-3 1845.42 2105 0.87 PPPSRC-2-4 1829.79 2176 0.84 PPPSRC-2-5 1829.79 1956 0.94 注:Vb为受弯承载力计算值;Vt为受弯承载力试验值。 本文尚对各国规范计算方法进行了对比分析,如表6所示。
表 6 基于现行规范的受剪承载力计算方法Table 6. The calculation method of shear capacity based on current standard规范 混凝土受剪
承载力Vc箍筋受剪
承载力Vsv型钢受剪
承载力Va预应力
筋受剪
承载力VpJGJ 138 \dfrac{ {1.75} }{ {\lambda + 1} }{f_{\text{t} } }b{h_0} {f_{ {\text{yv} } } }\dfrac{ { {A_{ {\text{sv} } } } } }{s}{h_0} \dfrac{ {0.58} }{\lambda }{A_{ {\text{sw} } } }{f_{\text{a} } } 0.05{N_{\text{p}}} JGJ 369 AISC 360 0.17{f_{\text{c}}}b{h_0} {f_{ {\text{yv} } } }\dfrac{ { {A_{ {\text{sv} } } } } }{s}{h_0} 0.6{A_{{\text{sw}}}}{f_{\text{a}}} 0.15{N_{\text{p}}} ACI 318 EC 4 0.18k{(100{\rho _s}{f_{\text{c} } })^{\tfrac{1}{3} } }b{h_0} 0.9{f_{ {\text{yv} } } }\dfrac{ { {A_{ {\text{sv} } } } } }{s}{h_0}\cot \theta \dfrac{ { {A_{ {\text{sw} } } }{f_{\text{a} } } }}{ {\sqrt 3 } } 0.15{N_{\text{p}}} EC 2 表7计算结果表明,由于规范公式基于半经验方法确定,其计算结果过于保守,计算精度明显劣于本文提出的计算方法。
表 7 各国规范受剪承载力计算结果Table 7. Calculation results of shear capacity in national norms试件编号 Vt/kN 中国规范 美国规范 欧洲规范 Vb/kN Vb/Vt Vb/kN Vb/Vt Vb/kN Vb/Vt PPSRC-2-1 2008 1449.59 0.72 1180.06 0.59 1164.69 0.58 PPPSRC-2-2 2005 1465.21 0.73 1226.93 0.61 1211.56 0.60 PPPSRC-2-3 2105 1480.84 0.70 1273.93 0.61 1258.43 0.60 PPPSRC-2-4 2176 1465.21 0.67 1226.93 0.56 1211.56 0.56 PPPSRC-2-5 1956 1465.21 0.75 1226.93 0.63 1211.56 0.62 注:Vb为受弯承载力计算值;Vt为受弯承载力试验值。 4.3 开裂荷载计算方法
对于本文提出的PPPSRC梁,由于预应力筋和超高性能混凝土的使用,其抗裂性能明显提升,其开裂荷载的计算方法如式(11)所示:
{M_{{\text{cr}}}} = \left( {{\sigma _{{\text{pc}}}} + \gamma {f_{{\text{tk}}}}} \right){W_0} (11) 式中:σpc为扣除全部预应力损失后,由预加力在抗裂验算边缘产生的混凝土预加应力,参考JGJ 369−2016[25];γ 为混凝土构件的截面抵抗矩塑性影响系数,γ = (0.7 +120/h)γm,对于矩形截面γm取1.55; ftk为与同龄期的混凝土立方体抗压强度相应的实际的混凝土轴心抗拉强度;W0为整梁换算截面下边缘的弹性抵抗矩。
按照上述计算方法计算的开裂荷载值见表8,其中Pcr,c=2Mcr/a,a为弯剪段长度。由表中数据可看出,部分预制预应力型钢混凝土梁的开裂荷载计算值与试验值符合较好。
表 8 开裂荷载试验值与计算值Table 8. Comparison between tested and calculated values of cracking load试件编号 Pcr,t/kN Pcr,c/kN Pcr,c / Pcr,t 平均值 变异系数 PPSRC-2-1 109 139.09 1.28 1.08 0.11 PPPSRC-2-2 140 161.29 1.15 PPPSRC-2-3 290 301.53 1.04 PPPSRC-2-4 276 275.87 1.00 PPPSRC-2-5 385 365.26 0.95 注:Pcr,t为开裂荷载试验值;Pcr,c为开裂荷载计算值。 5 结论
通过对8根PPPSRC梁及2根PPSRC梁的受弯和受剪性能试验研究,可以得出以下结论:
(1) PPPSRC梁破坏时,型钢、预制混凝土、现浇混凝土三者之间未发现粘结滑移裂缝,预制部分混凝土隔板可以较好地传递预制与现浇混凝土之间的纵向剪力,各部分共同工作性能良好。
(2) 在PPPSRC梁中,仅在预制部分施加预应力与全截面施加预应力开裂荷载和峰值荷载相差均在5%以内,说明通过部分预制能够达到等同现浇的受力性能。
(3) 预应力度和预制部分混凝土种类对PPPSRC梁的抗裂性能影响显著,其中PPPSRC梁的开裂荷载相较于普通型钢混凝土梁最高可提高166%,而预制部分采用超高性能混凝土,相比预制部分采用普通混凝土的试件开裂荷载可提高33%。
(4) 基于试验结果建立了适用于PPPSRC梁的受弯、受剪承载力以及开裂荷载的计算公式,计算结果与试验结果吻合较好。
-
表 1 试件设计主要参数及结果
Table 1 Main parameters and results of specimen design
研究内容 试件编号 预制/现浇混
凝土强度等级张拉控
制应力预应力度 预应力
布筋形式预应力
施加顺序预应力筋 预应力
施加高度预制/现浇混
凝土强度fcu/MPa开裂荷载
Pcr/kN极限荷载
Pu/kN受弯性能 PPSRC-1-1 C60/C50 − 0.00 − − − − 77.1/50.8 109 1182 PPPSRC-1-2 C60/C50 0.15fptk 0.06 直线型 A 2× 
− 61.5/52.9 140 1366 PPPSRC-1-3 C60/C50 0.40fptk 0.29 直线型 A 4× 
− 69.4/54.3 290 1397 PPPSRC-1-4 C60/C50 0.40fptk 0.29 直线型 B 4× 
− 66.7/60.4 276 1463 PPPSRC-1-5 C110/C50 0.40fptk 0.15 直线型 A 2× 
− 116.3/60.0 385 1486 受剪性能 PPSRC-2-1 C70/C40 − 0.00 − − − − 72.8/46.0 440 4017 PPPSRC-2-2 C70/C40 0.30fptk 0.06 直线型 A 4× 
C 72.8/46.0 620 4010 PPPSRC-2-3 C70/C40 0.60fptk 0.12 直线型 A 4× 
C 72.8/46.0 1220 4210 PPPSRC-2-4 C70/C40 0.30fptk 0.06 直线型 B 4× 
C 72.8/46.0 805 4352 PPPSRC-2-5 C70/C40 0.30fptk 0.06 直线型 B 4× 
D 72.8/46.0 795 3911 注:试件预应力施加顺序分为A、B两类,其中A类试件为预应力施加在预制梁上,B类试件为预应力施加在整梁上;试件的预应力施加高度分为C、D两类,其中C类试件预应力合力作用点距梁底104 mm,D类试件预应力合力作用点距梁底230 mm;fptk为预应力筋的极限强度标准值;fcu为立方体抗压强度平均值。 表 2 钢材力学性能
Table 2 Mechanical properties of steel
种类 直径或
厚度/mm屈服强度
fy/MPa极限强度
fu/ MPa弹性模量
Es/ MPa钢筋及预应力筋 6 432 624 2.10×105 8 354 537 2.10×105 20 427 612 2.00×105 25 430 625 2.10×105 32(精轧螺纹钢) 1103 1211 2.07×105 15.2(钢绞线) 1659 1952 1.95×105 型钢(Q235) 9 353 480 2.05×105 10 353 480 2.05×105 14 304 465 2.05×105 16 304 465 2.05×105 表 3 C110混凝土配合比设计
Table 3 Mix design of C110-grade concrete
质量比 钢纤维
体积掺量/(%)水泥 粉煤灰 矿粉 硅灰 砂 水 减水剂 1.00 0.25 0.08 0.08 1.34 0.28 0.03 2.5 表 4 受弯承载力试验值与计算值对比
Table 4 Comparison between tested and calculated values of flexural capacity
试件编号 试验
峰值
荷载
P^{\rm{t} }_{\rm{u} } /kN受弯
承载力
试验值
M^{\rm{t} }_{\rm{u} } /(kN·m)受弯
承载力
计算值
M^{\rm{c} }_{\rm{u} } /(kN·m)M^{\rm{c}}_{\rm{u}}/M^{\rm{t}}_{\rm{u}} 平均值 变异
系数PPSRC-1-1 1182.2 993.05 945.75 0.95 0.94 0.04 PPPSRC-1-2 1366.0 1147.44 1029.19 0.90 PPPSRC-1-3 1397.4 1173.82 1171.25 1.00 PPPSRC-1-4 1463.0 1228.92 1184.28 0.96 PPPSRC-1-7 1486.6 1248.74 1134.45 0.91 表 5 受剪承载试验值与计算值
Table 5 Comparison between tested and calculated values of shear strength
试件编号 Vb/kN Vt/kN Vb/Vt 平均值 变异系数 PPSRC-2-1 1814.17 2008 0.90 0.89 0.04 PPPSRC-2-2 1829.79 2005 0.92 PPPSRC-2-3 1845.42 2105 0.87 PPPSRC-2-4 1829.79 2176 0.84 PPPSRC-2-5 1829.79 1956 0.94 注:Vb为受弯承载力计算值;Vt为受弯承载力试验值。 表 6 基于现行规范的受剪承载力计算方法
Table 6 The calculation method of shear capacity based on current standard
规范 混凝土受剪
承载力Vc箍筋受剪
承载力Vsv型钢受剪
承载力Va预应力
筋受剪
承载力VpJGJ 138 \dfrac{ {1.75} }{ {\lambda + 1} }{f_{\text{t} } }b{h_0} {f_{ {\text{yv} } } }\dfrac{ { {A_{ {\text{sv} } } } } }{s}{h_0} \dfrac{ {0.58} }{\lambda }{A_{ {\text{sw} } } }{f_{\text{a} } } 0.05{N_{\text{p}}} JGJ 369 AISC 360 0.17{f_{\text{c}}}b{h_0} {f_{ {\text{yv} } } }\dfrac{ { {A_{ {\text{sv} } } } } }{s}{h_0} 0.6{A_{{\text{sw}}}}{f_{\text{a}}} 0.15{N_{\text{p}}} ACI 318 EC 4 0.18k{(100{\rho _s}{f_{\text{c} } })^{\tfrac{1}{3} } }b{h_0} 0.9{f_{ {\text{yv} } } }\dfrac{ { {A_{ {\text{sv} } } } } }{s}{h_0}\cot \theta \dfrac{ { {A_{ {\text{sw} } } }{f_{\text{a} } } }}{ {\sqrt 3 } } 0.15{N_{\text{p}}} EC 2 表 7 各国规范受剪承载力计算结果
Table 7 Calculation results of shear capacity in national norms
试件编号 Vt/kN 中国规范 美国规范 欧洲规范 Vb/kN Vb/Vt Vb/kN Vb/Vt Vb/kN Vb/Vt PPSRC-2-1 2008 1449.59 0.72 1180.06 0.59 1164.69 0.58 PPPSRC-2-2 2005 1465.21 0.73 1226.93 0.61 1211.56 0.60 PPPSRC-2-3 2105 1480.84 0.70 1273.93 0.61 1258.43 0.60 PPPSRC-2-4 2176 1465.21 0.67 1226.93 0.56 1211.56 0.56 PPPSRC-2-5 1956 1465.21 0.75 1226.93 0.63 1211.56 0.62 注:Vb为受弯承载力计算值;Vt为受弯承载力试验值。 表 8 开裂荷载试验值与计算值
Table 8 Comparison between tested and calculated values of cracking load
试件编号 Pcr,t/kN Pcr,c/kN Pcr,c / Pcr,t 平均值 变异系数 PPSRC-2-1 109 139.09 1.28 1.08 0.11 PPPSRC-2-2 140 161.29 1.15 PPPSRC-2-3 290 301.53 1.04 PPPSRC-2-4 276 275.87 1.00 PPPSRC-2-5 385 365.26 0.95 注:Pcr,t为开裂荷载试验值;Pcr,c为开裂荷载计算值。 -
[1] 薛建阳. 组合结构设计原理 [M]. 北京: 中国建筑工业出版社, 2010: 99 − 101. XUE Jianyang. Principle of composite structure design [M]. Beijing: China Architecture & Building Press, 2010: 99 − 101. (in Chinese)
[2] 傅传国, 李玉莹, 梁书亭. 预应力型钢混凝土简支梁受弯性能试验研究[J]. 建筑结构学报, 2007, 28(3): 62 − 73. doi: 10.3321/j.issn:1000-6869.2007.03.009 FU Chuanguo, LI Yuying, LIANG Shuting. Experimental study on simply supported prestressed steel reinforced concrete beams [J]. Journal of Building Structures, 2007, 28(3): 62 − 73. (in Chinese) doi: 10.3321/j.issn:1000-6869.2007.03.009
[3] 李峰. 预应力钢骨混凝土梁承载能力试验研究 [D]. 重庆: 重庆大学, 2007. LI Feng. Experimental research on the carrying capacity of the prestressed steel reinforced concrete beam [D]. Chongqing: Chongqing University, 2007. (in Chinese)
[4] 王钧, 邬丹, 郑文忠. 预应力H型钢混凝土简支梁正截面受力性能试验[J]. 哈尔滨工业大学学报, 2009, 41(6): 22 − 27. doi: 10.3321/j.issn:0367-6234.2009.06.005 WANG Jun, WU Dan, ZHENG Wenzhong. Experimental research on flexural mechanical behavior of simple prestressed H-steel reinforced concrete beam [J]. Journal of Harbin Institute of Technology, 2009, 41(6): 22 − 27. (in Chinese) doi: 10.3321/j.issn:0367-6234.2009.06.005
[5] 孟刚, 贾金青, 朱伟庆. 预应力型钢超高强混凝土梁抗弯性能试验研究[J]. 工程力学, 2014, 31(5): 203 − 210, 217. doi: 10.6052/j.issn.1000-4750.2012.11.0913 MENG Gang, JIA Jinqing, ZHU Weiqing. Experimental study on flexural behavior of prestressed steel reinforced ultra-high strength concrete beams [J]. Engineering Mechanics, 2014, 31(5): 203 − 210, 217. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.11.0913
[6] 贾金青, 姚大立, 余芳. 预应力型钢超高强混凝土梁受剪承载力试验研究[J]. 工程力学, 2014, 31(8): 126 − 133. doi: 10.6052/j.issn.1000-4750.2013.03.0155 JIA Jinqing, YAO Dali, YU Fang. Experimental study on shear capacity of prestressed I-steel ultrahigh reinforced concrete beams [J]. Engineering Mechanics, 2014, 31(8): 126 − 133. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.03.0155
[7] 贾金青, 孟刚, 封硕, 等. 预应力型钢超高强混凝土梁抗弯延性试验[J]. 哈尔滨工业大学学报, 2015, 47(4): 64 − 70. doi: 10.11918/j.issn.0367-6234.2015.04.011 JA Jinqing, MENG Gang, FENG Shuo, et al. Flexural ductility of prestressed steel reinforced ultra-high strength concrete beams [J]. Journal of Harbin Institute of Technology, 2015, 47(4): 64 − 70. (in Chinese) doi: 10.11918/j.issn.0367-6234.2015.04.011
[8] 熊学玉, 姚刚峰. 单调与反复竖向荷载作用下无黏结预应力型钢混凝土框架受力性能试验研究[J]. 建筑结构学报, 2017, 38(12): 1 − 11. doi: 10.14006/j.jzjgxb.2017.12.001 XIONG Xueyu, YAO Gangfeng. Experimental study on behavior of unbounded prestressed steel-reinforced concrete frame under vertical monotonic and cyclic loading [J]. Journal of Building Structures, 2017, 38(12): 1 − 11. (in Chinese) doi: 10.14006/j.jzjgxb.2017.12.001
[9] 高峰, 熊学玉. 预应力型钢混凝土框架结构竖向反复荷载作用下抗震性能试验研究[J]. 建筑结构学报, 2013, 34(7): 62 − 71. GAO Feng, XIONG Xueyu. Experimental study on seismic performance of prestressed steel reinforced concrete frame structure under vertical reversed loading [J]. Journal of Building Structures, 2013, 34(7): 62 − 71. (in Chinese)
[10] 杨勇, 薛亦聪, 于云龙, 等. 部分预制装配型钢混凝土梁受力性能试验研究[J]. 土木工程学报, 2018, 51(4): 1 − 9, 19. doi: 10.15951/j.tmgcxb.2018.04.001 YANG Yong, XUE Yicong, YU Yunlong, et al. Experimental research on mechanical performance of partially precast steel reinforced concrete beams [J]. China Civil Engineering Journal, 2018, 51(4): 1 − 9, 19. (in Chinese) doi: 10.15951/j.tmgcxb.2018.04.001
[11] 杨勇, 薛亦聪, 于云龙, 等. 部分预制装配型钢混凝土梁受弯性能试验研究[J]. 建筑结构学报, 2017, 38(9): 46 − 53. doi: 10.14006/j.jzjgxb.2017.09.006 YANG Yong, XUE Yicong, YU Yunlong, et al. Experimental study of partially precast steel reinforced concrete beams under positive bending [J]. Journal of Building Structures, 2017, 38(9): 46 − 53. (in Chinese) doi: 10.14006/j.jzjgxb.2017.09.006
[12] 杨勇, 陈阳, 张锦涛, 等. 部分预制装配型钢混凝土构件斜截面抗剪承载能力试验研究[J]. 工程力学, 2019, 36(4): 109 − 116. doi: 10.6052/j.issn.1000-4750.2018.01.0071 YANG Yong, CHEN Yang, ZHANG Jintao, et al. Experimental study on the oblique section shear capacity of partially prefabricated steel reinforced concrete (PPSRC) members [J]. Engineering Mechanics, 2019, 36(4): 109 − 116. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.01.0071
[13] 杨勇, 薛亦聪, 于云龙. 预制装配型钢混凝土梁受剪承载力试验与计算方法研究[J]. 工程力学, 2019, 36(6): 92 − 100. doi: 10.6052/j.issn.1000-4750.2018.04.0217 YANG Yong, XUE Yicong, YU Yunlong. Research on the shear strength of precast steel reinforced concrete beams [J]. Engineering Mechanics, 2019, 36(6): 92 − 100. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.04.0217
[14] NZABONIMPA J D, HONG W K, KIM J. Strength and post-yield behavior of T-section steel encased by structural concrete [J]. The Structural Design of Tall and Special Buildings, 2018, 27(5): e1447. doi: 10.1002/tal.1447
[15] HONG W K, PARK S C, KIM J M, et al. Composite beam composed of steel and precast concrete (Modularized Hybrid System, MHS). Part I: Experimental investigation [J]. The Structural Design of Tall and Special Buildings, 2010, 19(3): 275 − 289.
[16] HONG W K, KIM J M, PARK S C, et al. Composite beam composed of steel and pre-cast concrete (Modularized Hybrid System, MHS). Part II: Analytical investigation [J]. The Structural Design of Tall and Special Buildings, 2009, 18(8): 891 − 905. doi: 10.1002/tal.484
[17] HONG W K, PARK S C, LEE H C, et al. Composite beam composed of steel and precast concrete (Modularized Hybrid System, MHS). Part III: Application for a 19-storey building [J]. The Structural Design of Tall and Special Buildings, 2010, 19(6): 679 − 706. doi: 10.1002/tal.507
[18] HONG W K, KIM S I, PARK S C, et al. Composite beam composed of steel and precast concrete (Modularized Hybrid System, MHS). Part IV: Application for multi-residential housing [J]. The Structural Design of Tall and Special Buildings, 2010, 19(7): 707 − 727.
[19] DBJ 43/T 325−2017, 活性粉末混凝土结构技术规程 [S]. 北京: 中国建筑工业出版社, 2017. DBJ 43/T 325−2017, Technical specification for reactive powder concrete structures [S]. Beijing: China Architec-ture & Building Press, 2017. (in Chinese)
[20] JGJ 138−2016, 组合结构设计规范 [S]. 北京: 中国建筑工业出版社, 2016. JGJ 138−2016, Code for design of composite structures [S]. Beijing: China Architecture & Building Press, 2016. (in Chinese)
[21] GB 50010−2010, 混凝土结构设计规范 [S]. 北京: 中国建筑工业出版社, 2011. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[22] 邓明科, 宋诗飞, 张敏, 等. 高延性混凝土加固钢筋混凝土梁受剪性能试验研究及承载力计算[J]. 工程力学, 2021, 38(9): 36 − 44, 63. doi: 10.6052/j.issn.1000-4750.2020.06.0381 DENG Mingke, SONG Shifei, ZHANG Min, et al. Experimental study on shear behavior and capacity prediction of RC beams strengthened with high ductile concrete [J]. Engineering Mechanics, 2021, 38(9): 36 − 44, 63. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0381
[23] 贡金鑫, 魏巍巍, 赵尚传. 现代混凝土结构基本理论及应用 [M]. 北京: 中国建筑工业出版社, 2009: 229 − 231. GONG Jinxin, WEI Weiwei, ZHAO Shangchuan. Basic theory and application of modern concrete structures [M]. Beijing: China Architecture & Building Press, 2009: 229 − 231. (in Chinese)
[24] YB 9082−2006, 钢骨混凝土结构技术规程 [S]. 北京: 冶金工业出版社, 1998. YB 9082−2006, Technical specification of steel-reinforced concrete structures [S]. Beijing: Metallurgical Industry Press, 1998. (in Chinese)
[25] JGJ 369−2016, 预应力混凝土结构设计规范 [S]. 北京: 中国建筑工业出版社, 2016. JGJ 369−2016, Code for design of prestressed concrete structures [S]. Beijing: China Architecture & Building Press, 2016. (in Chinese)
-
期刊类型引用(9)
1. 刘旭宏,祁皑,罗才松,黄凯. 基于双重壳模型的钢筋黏结滑移有限元模拟. 工程抗震与加固改造. 2022(03): 23-29 .  百度学术
百度学术
2. 赵发军,李建. 基于ABAQUS的复合箍筋约束轻骨料混凝土柱偏压力学性能研究. 中国测试. 2022(09): 171-176+184 .  百度学术
百度学术
3. 陈宇良,朱玲,吉云鹏,吴辉琴,叶培欢. 三轴受压粉煤灰陶粒轻骨料混凝土力学性能试验. 复合材料学报. 2022(10): 4801-4812 .  百度学术
百度学术
4. 万宇通,郑文忠,王英. 网格箍筋约束混凝土柱轴压受力性能试验研究. 工程力学. 2022(11): 166-176 .  本站查看
本站查看
5. 牛建刚,许文明,梁剑. 受压区局部约束塑钢纤维轻骨料混凝土梁的抗弯性能. 材料导报. 2021(08): 8056-8063 .  百度学术
百度学术
6. 李磊,王卓涵,张艺欣,郑山锁. 混凝土结构中考虑滑移效应的钢筋本构模型研究. 工程力学. 2020(03): 88-97 .  本站查看
本站查看
7. 邓宗才,姚军锁. 高强钢筋约束超高性能混凝土柱轴心受压本构模型研究. 工程力学. 2020(05): 120-128 .  本站查看
本站查看
8. 赵恩亮. 不同侧向应力作用下轻骨料混凝土力学性能研究. 新型建筑材料. 2020(05): 17-21 .  百度学术
百度学术
9. 周天华,余吉鹏,李亚鹏,张钰. 单轴对称十字型钢混凝土短柱轴压性能试验研究. 工程力学. 2020(12): 157-170 .  本站查看
本站查看
其他类型引用(14)



 下载:
下载: