STUDY ON ANALYTICAL MODEL OF TUNNEL MECHANICAL RESPONSE CONSIDERING CONSTRUCTION INTERRUPTION
-
摘要:
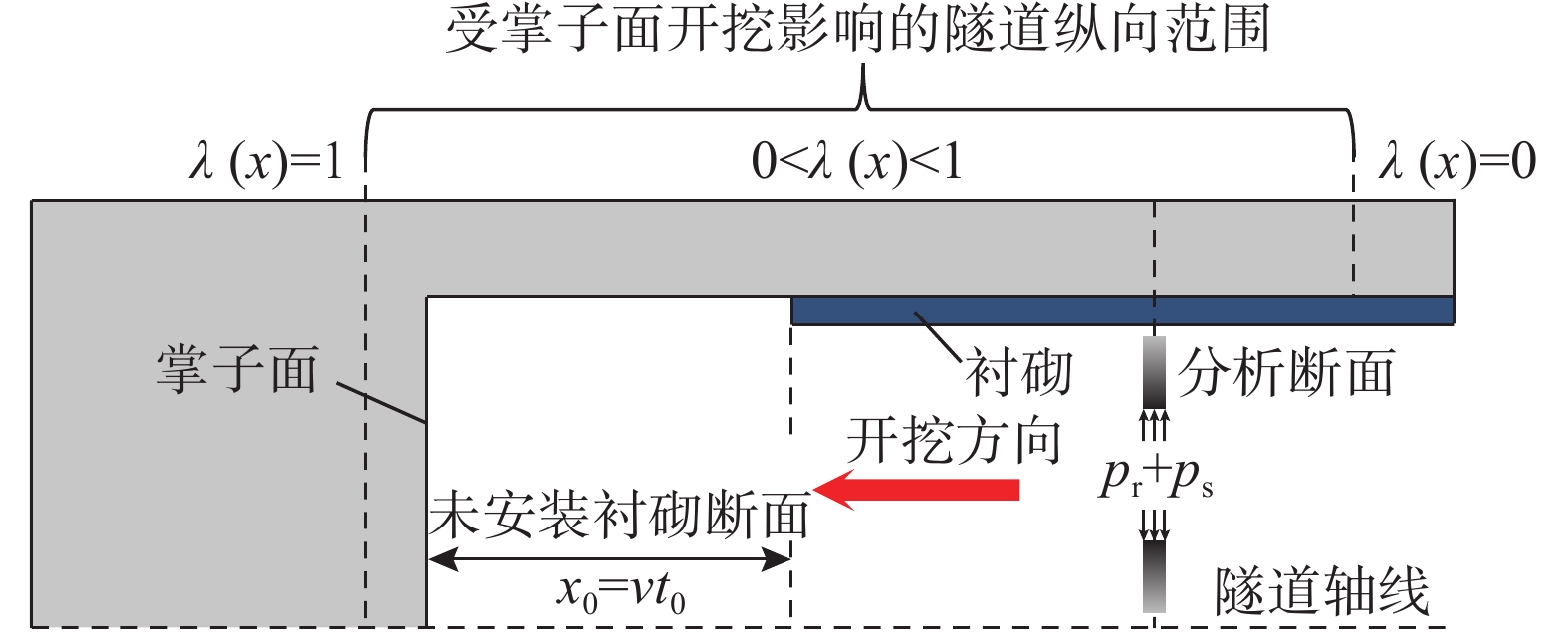
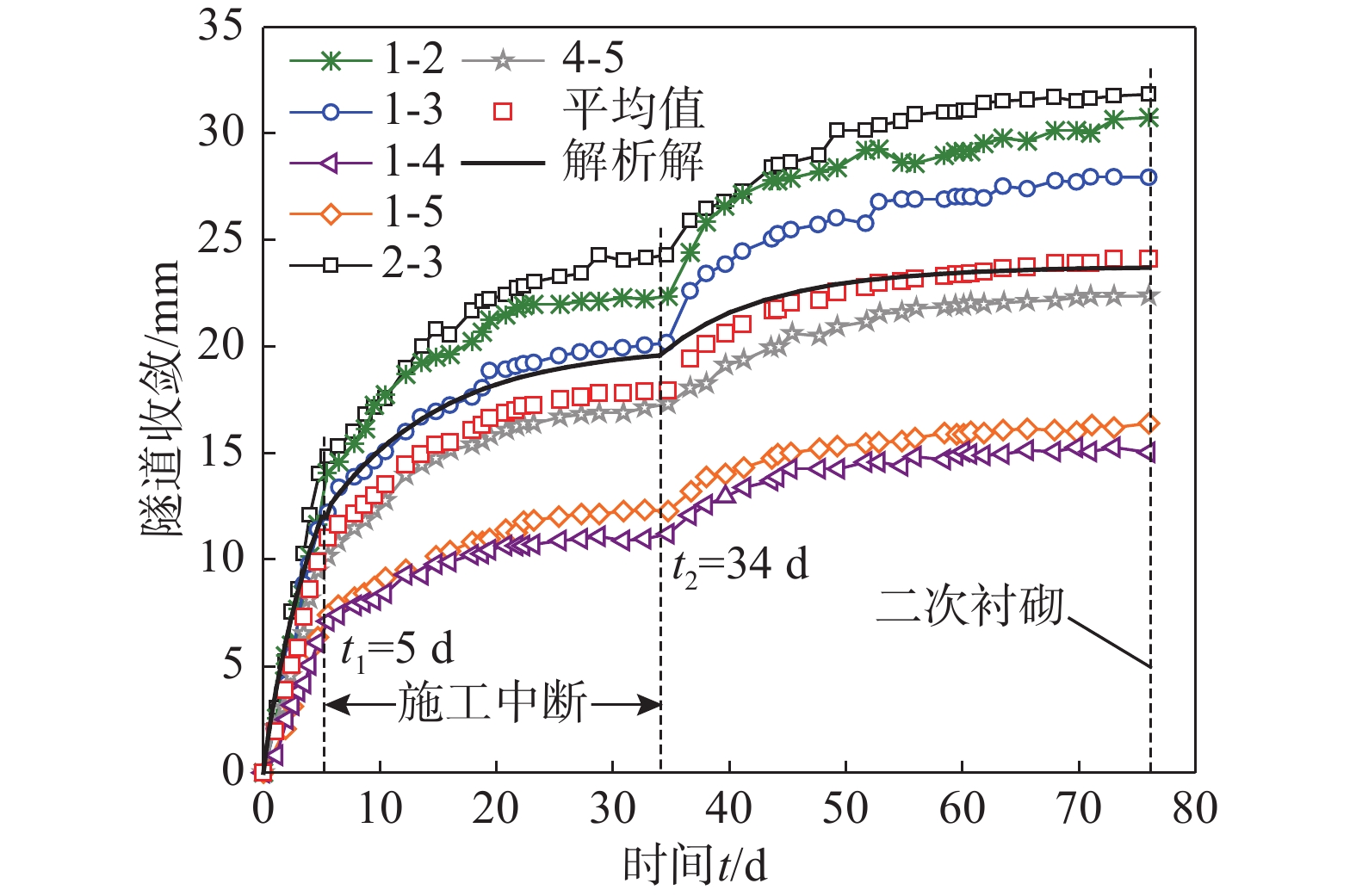
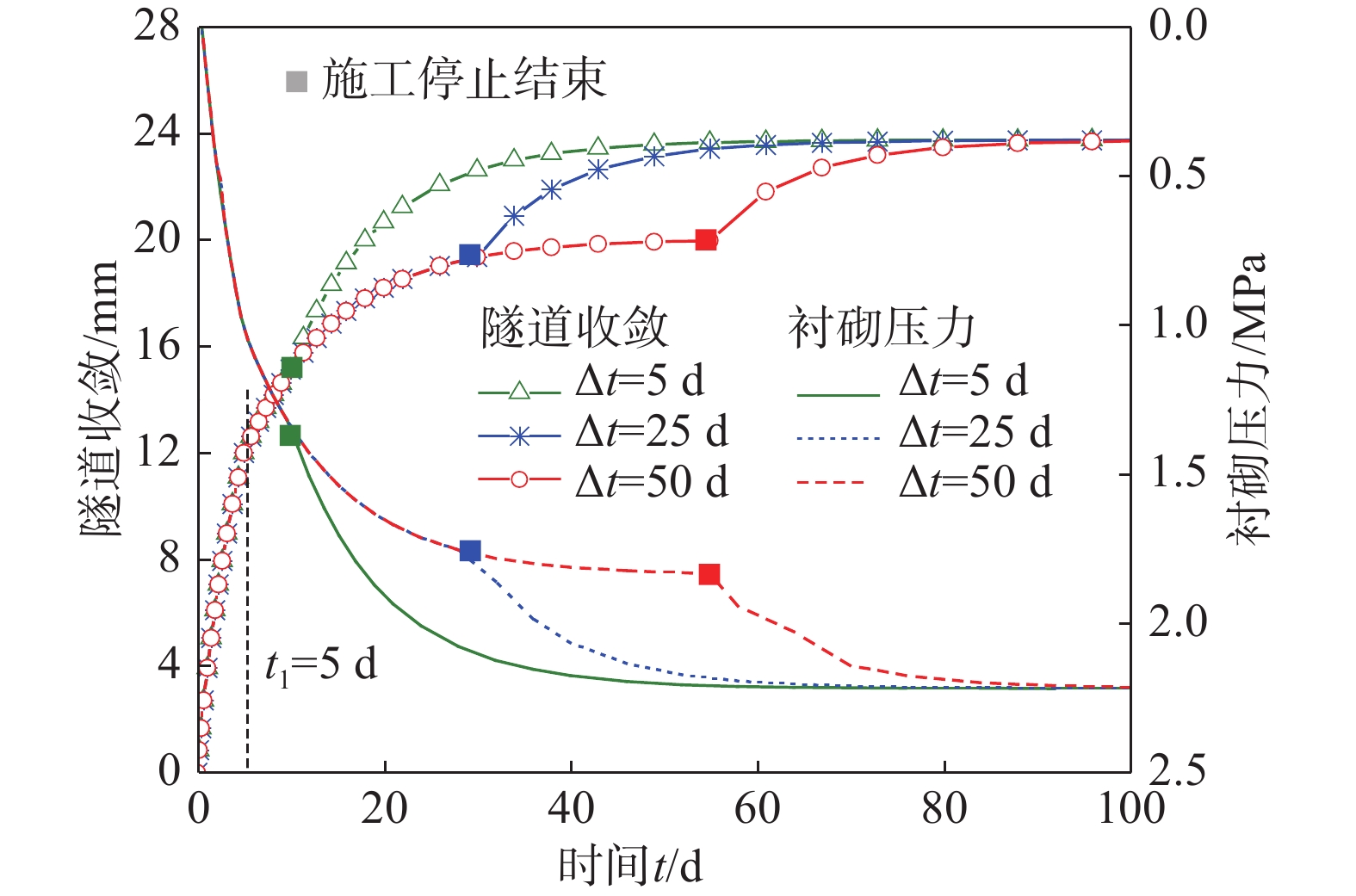
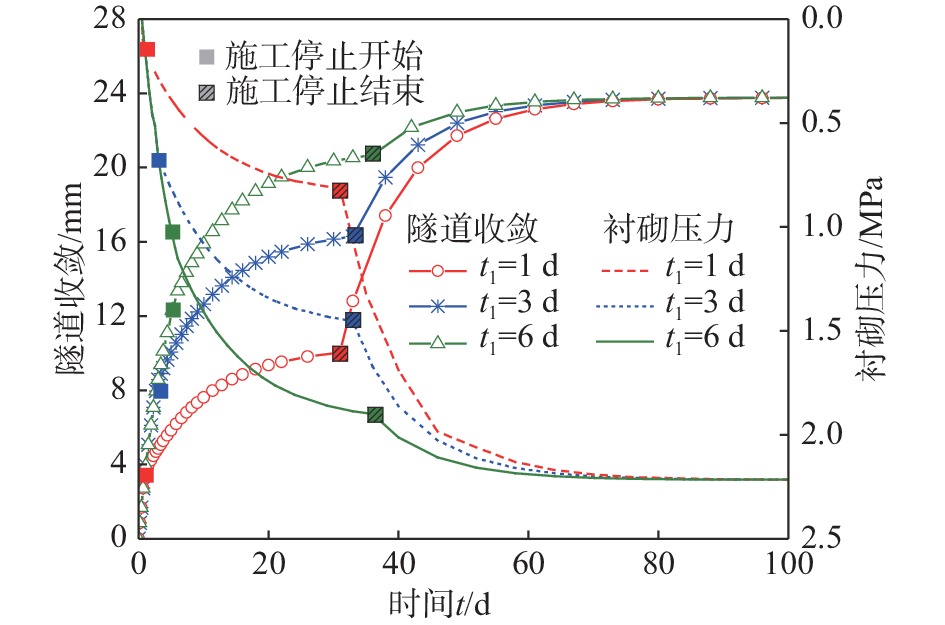
在具有显著时效变形特征的软岩地层中进行隧道挖掘时，因不可抗力因素导致的施工中断可能会对隧道后方衬砌产生不利影响，从而增加了隧道施工的风险。因此，准确评估隧道纵向施工中断，对硐室围岩和衬砌长期稳定性的影响具有重要意义。为揭示隧道施工中断条件下围岩与衬砌相互作用的力学机制，采用应力释放系数将三维隧道开挖问题等效为二维平面应变问题，并基于经典的负指数型应力释放系数表达式，建立了考虑施工中断工况时改进的表达式。进一步，利用广义Kelvin流变模型表征围岩的时效变形行为，推导了隧道施工过程中考虑施工中断和支护结构滞后安装的时空变形解析解。通过在郑万高铁荣家湾隧道中的应用，上述理论解答的正确性得到了很好的验证。基于理论解答，探讨了施工中断持续时间、中断开始时间以及开挖速度等因素对隧道位移和衬砌压力的影响。参数分析结果表明，由掌子面推进引起的衬砌压力可占总压力的17.3%。施工中断持续时间和开始时间对隧道位移和衬砌压力的演化规律具有重要影响，但对最终的位移和压力的影响可忽略不计。施工中断前的开挖速度越大，最终由掌子面承担的围岩压力减小。当应力释放系数达到0.8时，再次重新挖掘的速度对隧道稳定性几乎没有影响。
Abstract:When tunneling in soft rock stratum with significant time-dependent deformation characteristics, the construction interruption caused by force majeure may generate adverse effects on tunnel linings, resulting in the increase of tunnel construction risk. Therefore, it is a very important task to accurately evaluate the influence of construction interruption on the long-term stability of surrounding rocks and linings. In order to investigate the interaction mechanism between surrounding rocks and linings, the three-dimensional tunnel excavation problem is equivalent to a two-dimensional plane strain one by using the stress release coefficient. The improved expression is established, which is based on the classical stress release coefficient expression in the negative exponential form and takes the construction interruption into account. Furthermore, by using the generalized Kelvin model describing the time-dependent behaviour of surrounding rocks, the analytical solution for temporal and spatial tunnel deformation is derived, where the construction interruption and delay installation of lining structures are considered. Through its application in Rongjiawan tunnel of Zhengwan high speed railway, the theoretical derivation provided is well verified. A parametric investigation is carried out based on the previous analytical solution, including duration and start time of construction interruption and excavation rate. It can be found that the lining pressure caused by the tunnel face advancement contributes about 17.3% of the total lining pressure. The duration and start time of construction interruption exhibit a significant influence on the developments of tunnel displacement and lining pressure, but do not show obvious influence on the final tunnel displacement and lining pressure. A greater excavation rate before the construction interruption leads to a decreasing rock pressure born by the tunnel face. When the stress release coefficient value reaches 0.8, the influence of the excavation rate after the excavation rate can be basically ignored.
-
Keywords:
- tunnel /
- rheology /
- construction interruption /
- interaction /
- analytical solution
-
-
![]()
图 1 考虑施工停止的应力释放系数曲线
Figure 1. Curves for the stress release coefficient considering the excavation stoppage
![]()
图 2 掌子面开挖空间效应示意图
Figure 2. Illustration for spatial effect triggered by tunnel face excavation
![]()
图 5 荣家湾隧道掌子面和监控量测布置图
Figure 5. Tunnel face of Rongjia wan tunnel and layout of monitoring points
![]()
图 6 荣家湾隧道监测收敛与理论结果对比
Figure 6. Comparison of tunnel convergence between monitoring and theoretical results
![]()
图 7 荣家湾隧道监测衬砌压力与理论结果对比
Figure 7. Comparison of lining pressure between monitoring and theoretical results
![]()
图 8 不同施工中断持续时间下隧道收敛与衬砌压力曲线
Figure 8. Curves of tunnel convergence and lining pressure under different durations of interruption
![]()
图 9 不同施工中断开始时间下隧道收敛与衬砌压力曲线
Figure 9. Curves of tunnel convergence and lining pressure under different starting times of interruption
![]()
图 10 不同开挖速度下隧道收敛与衬砌压力曲线
Figure 10. Curves of tunnel convergence and lining pressure under different excavation rates
表 1 荣家湾隧道参数
Table 1 Parameters of Rongjia wan tunnel
参数名称 数值 隧道半径r0/m 5.7 初始地应力p0/MPa 9.5 剪切模量G1/GPa 3.1 剪切模量G2/GPa 2.6 黏滞系数η/(GPa·d) 31.2 衬砌厚度ts/m 0.25 衬砌弹性模量Es/GPa 24 泊松比νs 0.25 初始释放系数α 0.68 影响半径RL/m 6.875 开挖速率v1/(m·d−1) 2.2 开挖速率v2/(m·d−1) 1.6 衬砌安装时间t0/d 0.5 施工停止起始时t1/d 5 施工停止结束时t2/d 34 
下载: 导出CSV
-
[1] FAHIMIFAR A, TEHRANI F M, HEDAYAT A, et al. Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field [J]. Tunnelling and Underground Space Technology, 2010, 25(4): 297 − 304. doi: 10.1016/j.tust.2010.01.002
[2] YAO Y M, LU N, YANG Y M, et al. Study of long-termed displacements of a tunnel boring machine during its stoppage [J]. Tunnelling and Underground Space Technology, 2019, 84: 432 − 439. doi: 10.1016/j.tust.2018.11.041
[3] TRAN-MANH H, SULEM J, SUBRIN D. Progressive degradation of rock properties and time-dependent behavior of deep tunnels [J]. Acta Geotechnica, 2016, 11(3): 693 − 711. doi: 10.1007/s11440-016-0444-x
[4] 吴奎, 邵珠山, 秦溯. 流变岩体中让压支护作用下隧道力学行为研究[J]. 力学学报, 2020, 52(3): 890 − 900. WU Kui, SHAO Zhushan, QIN Su. Investigation on the mechanical behavior of tunnel supported by yielding supports in rheological rocks [J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(3): 890 − 900. (in Chinese)
[5] 孙振宇, 张顶立, 刘道平, 等. 锚固体系作用下隧道围岩力学响应的全过程解析[J]. 工程力学, 2022, 39(7): 170 − 182. doi: 10.6052/j.issn.1000-4750.2021.04.0274 SUN Zhenyu, ZHANG Dingli, LIU Daoping, et al. Analysis of the whole-process mechanical response of tunnel surrounding rock under the effect of anchorage system [J]. Engineering Mechanics, 2022, 39(7): 170 − 182. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.04.0274
[6] 储昭飞, 刘保国, 刘开云, 等. 非静水应力场中圆形隧道衬砌与围岩间两种接触的黏弹性解析[J]. 岩土力学, 2017, 38(11): 3215 − 3224. doi: 10.16285/j.rsm.2017.11.017 CHU Zhaofei, LIU Baoguo, LIU Kaiyun, et al. Analytical viscoelastic solutions for lined circular tunnels under two contact conditions in a non-hydrostatic stress field [J]. Rock and Soil Mechanics, 2017, 38(11): 3215 − 3224. (in Chinese) doi: 10.16285/j.rsm.2017.11.017
[7] 郑颖人, 朱合华, 方正昌, 等. 地下工程围岩稳定分析与设计理论 [M]. 北京: 人民交通出版社, 2012: 26 − 94. ZHENG Yingren, ZHU Hehua, FANG Zhengchang, et al. Stability analysis and design theory of surrounding rock of underground engineering [M]. Beijing: China Communications Press, 2012: 26 − 94. (in Chinese)
[8] EINSTEIN H H, SCHWARTZ C W. Simplified analysis for tunnel supports [J]. Journal of the Geotechnical Engineering Division, 1979, 105(4): 499 − 518. doi: 10.1061/AJGEB6.0000786
[9] VERRUIJT A. A complex variable solution for a deforming circular tunnel in an elastic half-plane [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(2): 77 − 89. doi: 10.1002/(SICI)1096-9853(199702)21:2<77::AID-NAG857>3.0.CO;2-M
[10] EXADAKTYLOS G E, STAVROPOULOU M C. A closed-form elastic solution for stresses and displacements around tunnels [J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(7): 905 − 916. doi: 10.1016/S1365-1609(02)00079-5
[11] CARRANZA-TORRES C, RYSDAHL B, KASIM M. On the elastic analysis of a circular lined tunnel considering the delayed installation of the support [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 57 − 85. doi: 10.1016/j.ijrmms.2013.01.010
[12] 李岩松, 陈寿根. 基于复变函数理论的非圆形隧道解析解[J]. 西南交通大学学报, 2020, 55(2): 265 − 272. doi: 10.3969/j.issn.0258-2724.20180243 LI Yansong, CHEN Shougen. Lining and surrounding rock in non-circular tunnel based on complex variable method [J]. Journal of Southwest Jiaotong University, 2020, 55(2): 265 − 272. (in Chinese) doi: 10.3969/j.issn.0258-2724.20180243
[13] MALAN D F. Manuel Rocha medal recipient simulating the time-dependent behaviour of excavations in hard rock [J]. Rock Mechanics and Rock Engineering, 2002, 35(4): 225 − 254. doi: 10.1007/s00603-002-0026-0
[14] FRITZ P. An analytical solution for axisymmetric tunnel problems in elasto-viscoplastic media [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1984, 8(4): 325 − 342. doi: 10.1002/nag.1610080403
[15] CRISTESCU N, FOTǍ D, MEDVEŞ E. Tunnel support analysis incorporating rock creep [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1987, 24(6): 321 − 330.
[16] NOMIKOS P, RAHMANNEJAD R, SOFIANOS A. Supported axisymmetric tunnels within linear viscoelastic Burgers rocks [J]. Rock Mechanics and Rock Engineering, 2011, 44(5): 553 − 564. doi: 10.1007/s00603-011-0159-0
[17] BIRCHALL T J, OSMAN A S. Response of a tunnel deeply embedded in a viscoelastic medium [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(15): 1717 − 1740. doi: 10.1002/nag.1069
[18] WANG H N, LI Y, NI Q, et al. Analytical solutions for the construction of deeply buried circular tunnels with two liners in rheological rock [J]. Rock Mechanics and Rock Engineering, 2013, 46(6): 1481 − 1498. doi: 10.1007/s00603-012-0362-7
[19] 王华宁, 宋飞, 蒋明镜. 流变岩体中支护圆形隧道施工过程的时效理论解[J]. 同济大学学报(自然科学版), 2016, 44(12): 1835 − 1844. doi: 10.11908/j.issn.0253-374x.2016.12.005 WANG Huaning, SONG Fei, JIANG Mingjing. Analytical solutions for the construction of circular tunnel accounting for time-dependent characteristic of the rheological rock [J]. Journal of Tongji University (Natural Science), 2016, 44(12): 1835 − 1844. (in Chinese) doi: 10.11908/j.issn.0253-374x.2016.12.005
[20] 王华宁, 曾广尚, 蒋明镜. 流变岩体中既有隧道与新建平行隧道相互影响的理论解[J]. 岩土工程学报, 2015, 37(8): 1365 − 1374. doi: 10.11779/CJGE201508002 WANG Huaning, ZENG Guangshang, JIANG Mingjing. Analytical solutions for interaction between existing and new tunnels parallel excavated in rheological rock mass [J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1365 − 1374. (in Chinese) doi: 10.11779/CJGE201508002
[21] LUKIC D C, ZLATANOVIC E M, JOKANOVIC I M. Tunnel lining load with consideration of the rheological properties of rock mass and concrete [J]. Geomechanics and Engineering, 2020, 21(1): 53 − 62.
[22] 张常光, 曾开华. 收敛约束法中隧道开挖面空间效应方法比较[J]. 岩土力学, 2016, 37(5): 1417 − 1424. doi: 10.16285/j.rsm.2016.05.025 ZHANG Changguang, ZENG Kaihua. Comparisons of spatial-effect approaches for tunnel excavation using convergence-confinement method [J]. Rock and Soil Mechanics, 2016, 37(5): 1417 − 1424. (in Chinese) doi: 10.16285/j.rsm.2016.05.025
[23] 崔岚, 郑俊杰, 苗晨曦, 等. 隧道纵向变形曲线与围岩特征曲线耦合分析[J]. 岩土工程学报, 2014, 36(4): 707 − 715. doi: 10.11779/CJGE201404015 CUI Lan, ZHENG Junjie, MIAO Chenxi, et al. Coupling analysis of longitudinal deformation profile and ground reaction curve [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 707 − 715. (in Chinese) doi: 10.11779/CJGE201404015
[24] KONTOGIANNI V, PSIMOULIS P, STIROS S. What is the contribution of time-dependent deformation in tunnel convergence? [J]. Engineering Geology, 2006, 82(4): 264 − 267. doi: 10.1016/j.enggeo.2005.11.001
[25] WU K, SHAO Z S, QIN S. An analytical design method for ductile support structures in squeezing tunnels [J]. Archives of Civil and Mechanical Engineering, 2020, 20(3): 91. doi: 10.1007/s43452-020-00096-0
[26] PANET M, GUENOT A. Analysis of convergence behind the face of a tunnel [C]// Proceedings of the 3rd International Symposium. London: IMM, 1982: 197 − 204.
[27] PANET M. Calcul des tunnels par la me’thode de convergence-confinement [M]. Paris: Presses de l’Ecole Nationale des Ponts et Chausse’es, 1995: 98 − 120.
[28] UNLU T, GERCEK H. Effect of Poisson’s ratio on the normalized radial displacements occurring around the face of a circular tunnel [J]. Tunnelling and Underground Space Technology, 2003, 18(5): 547 − 553. doi: 10.1016/S0886-7798(03)00086-5
[29] VLACHOPOULOS N, DIEDERICHS M S. Improved longitudinal displacement profiles for convergence confinement analysis of deep tunnels [J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 131 − 146. doi: 10.1007/s00603-009-0176-4
[30] SULEM J, PANET M, GUENOT A. An analytical solution for time-dependent displacements in a circular tunnel [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1987, 24(3): 155 − 164.
[31] 张建智, 俞缙, 张小燕, 等. 岩质隧道施工过程变形时空问题的位移释放系数法[J]. 工程科学与技术, 2019, 51(2): 98 − 107. ZHANG Jianzhi, YU Jin, ZHANG Xiaoyan, et al. Displacement release coefficient method for spatiotemporal deformations of rocky tunnels during construction [J]. Advanced Engineering Sciences, 2019, 51(2): 98 − 107. (in Chinese)
[32] 吴奎, 邵珠山, 秦溯. 挤压隧道中围岩与内置高压缩性元件衬砌相互作用机制研究[J]. 工程力学, 2020, 37(11): 185 − 194. doi: 10.6052/j.issn.1000-4750.2020.01.0013 WU Kui, SHAO Zhushan, QIN Su. Study on the interaction mechanism between surrounding rock and liner with highly deformable elements in squeezing tunnels [J]. Engineering Mechanics, 2020, 37(11): 185 − 194. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.01.0013
[33] 卞跃威, 夏才初, 肖维民, 等. 考虑围岩软化特性和应力释放的圆形隧道黏弹塑性解[J]. 岩土力学, 2013, 34(1): 211 − 220. doi: 10.16285/j.rsm.2013.01.017 BIAN Yuewei, XIA Caichu, XIAO Weimin, et al. Visco-elastoplastic solutions for circular tunnel considering stress release and softening behaviour of rocks [J]. Rock and Soil Mechanics, 2013, 34(1): 211 − 220. (in Chinese) doi: 10.16285/j.rsm.2013.01.017
[34] 刘昌, 张顶立, 孙振宇, 等. 初支混凝土硬化特性与围岩流变耦合作用机制[J]. 工程力学, 2023, 40(1): 63 − 75, 86. doi: 10.6052/j.issn.1000-4750.2021.08.0619 LIU Chang, ZHANG Dingli, SUN Zhenyu, et al. Interaction mechanism between primary support and rheological surrounding rock considering hardening performance of shotcrete [J]. Engineering Mechanics, 2023, 40(1): 63 − 75, 86. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.08.0619
[35] ZHAO D P, JIA L L, WANG M N, et al. Displacement prediction of tunnels based on a generalised Kelvin constitutive model and its application in a subsea tunnel [J]. Tunnelling and Underground Space Technology, 2016, 54: 29 − 36. doi: 10.1016/j.tust.2016.01.030
[36] KARGAR A R, RAHMANNEJAD R, HAJABASI M A. A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method [J]. International Journal of Solids and structures, 2014, 51(6): 1475 − 1482. doi: 10.1016/j.ijsolstr.2013.12.038
-
期刊类型引用(13)
1. 王俊超，李成钰，李馨馨. 基于MC-DFN模拟的EGS采热影响研究. 太阳能学报. 2025(03): 91-99 . 
百度学术
2. 梁万，李硕，田霄. 裂隙网络参数对渗流传热特性的影响研究. 现代矿业. 2025(04): 118-124 . 百度学术
3. 周家兴，王金安，李飞. 深部工程岩体温度与渗流耦合作用下复杂应力场反演方法. 工程力学. 2024(06): 188-201 . 本站查看
4. 左玉妹，成建梅，赵锐锐，刘浩田，吴凡，谢先军，梁腾飞. 英山地热田区深大断裂的控水控热作用及地热系统成因研究. 水文地质工程地质. 2024(04): 220-232 . 百度学术
5. 高俊义. 地热井倾斜度对热采效率影响的三维数值分析. 地球物理学进展. 2024(05): 1763-1770 . 百度学术
6. 孟川杰. 基于虚拟影像探查的深部裂隙岩体储水分布探测研究. 中国测试. 2022(03): 53-58 . 百度学术
7. 张进平，王煜曦，刘桂宏，何铁柱，袁利娟，徐浩然，孔祥军. 通州区地热资源优化开采模式动态研究. 工程力学. 2022(06): 247-256 . 本站查看
8. 王奕雅，于海龙，黄刘洋，刘丽，吴曙程，朱宝忠，孙运兰，刘恩海. 干热岩增强型地热系统平行三裂隙传热影响因素分析. 可再生能源. 2022(09): 1181-1188 . 百度学术
9. 符韵梅，董艳辉，谢月清，周志超，王礼恒，张明. 基于分布式光纤温度示踪探测裂隙岩体地下水渗流特征. 工程地质学报. 2022(04): 1257-1265 . 百度学术
10. 陈金龙，罗文行，窦斌，周洋，宁文涛. 涿鹿盆地三维多裂隙地质模型地温场数值模拟. 地质科技通报. 2021(03): 22-33 . 百度学术
11. 韩智铭，刘庆宽，王雪，谭超，高一帆. 岩体多裂纹扩展演化过程数值流形方法研究. 工程力学. 2021(S1): 7-13 . 本站查看
12. 高俊义. 地热温度和生产井深度对岩体水流-传热温度影响机理研究. 地球物理学进展. 2020(05): 1659-1664 . 百度学术
13. 高俊义. 裂隙参数对岩体水流-传热温度影响的数值模拟分析. 水资源与水工程学报. 2019(06): 206-211 . 百度学术
其他类型引用(15)
计量
- 文章访问数: 162
- HTML全文浏览量: 41
- PDF下载量: 36
- 被引次数: 28
