福建省紧邻地震最为活跃的中国台湾地震带，近年来中国台湾海峡地震频发，对该地区造成了不同程度的破坏，地震形势十分严峻。同时，福建沿海地区广泛分布着众多的石结构建筑，这些建筑主要由石柱、石墙、石梁和石楼板构成(如图1)，其中石楼板是石结构建筑中特有的一种楼板形式^[1]，由于石材本身含有自然裂缝且属于脆性材料，在地震作用的影响下，一旦石楼板发生开裂，其承载能力会迅速丧失，容易发生脆性破坏^[2-3]，从而造成严重的人员伤亡与财产损失。为了提升石材受弯构件在日常情况下的承载能力以及在突发情况下的变形能力，众多学者相继提出了各种加固技术，并进行了相应的试验与理论研究。

图  1  石结构建筑及其构件示意图

Figure  1.  Schematic diagram of stone structure building and its components

下载: 全尺寸图片 幻灯片

张兴虎等^[4]、谢剑等^[5]深入探讨了预应力技术在加固石梁中的应用，并发现通过预应力加固技术的运用，石梁的弯曲承载能力得到了显著增强。此外，这种技术的应用也极大地扩展了石材构件的使用领域。张丰宇等^[6]、XIE等^[7]、李梁峰^[8]和MIAO等^[9]提出利用粘钢加固技术和预应力钢丝绳加固石梁、石板能有效提高构件的变形能力与抗弯承载力。GUO等^[10-11]对应用钢筋网改性砂浆加固石板的抗弯性能进行了深入研究。研究结果表明：加固后石板破坏模式呈现出明显的延性破坏特点。同时，随着配筋率的提高以及钢筋强度等级的增加，加固石板的抗弯性能得到了显著改善。

近年来纤维增强复合材料(FRP)因其高强、耐久性好、自重轻^[12-13]等优点广泛应用于石结构加固。SHRIVE等^[14]指出FRP能够有效提升石材的抗拉强度和抗压强度，通过增强材料韧性来延缓裂纹的扩展，显著提高了石结构的抗震性能。武晓敏等^[15-16]对采用体外预应力技术和CFRP加固技术加固后石梁的抗弯性能进行了比较研究。分析结果表明：石梁的极限承载力主要受石材本身的材质特性及其初始缺陷的影响。WEI等^[17]通过试验研究得到CFRP加固石材受弯构件的承载力与CFRP用量的关联性。FAYALA等^[18]通过试验和数值模拟分析了GFRP加固石梁的破坏模式。刘阳等^[19-20]、GAO等^[21]提出嵌埋CFRP筋加固技术能显著提高石梁板的抗弯性能，同时着重提出在采用预应力CFRP加固技术对石材受弯构件进行加固时，CFRP筋两端的锚固效果决定了加固后石梁的受弯性能。在此基础上YE等^[22-23]进一步探讨了预应力表层嵌贴CFRP对石材受弯构件的加固效果，特别分析了有无预应力加持以及不同预应力水平下CFRP对石材受弯构件抗弯性能的影响。为避免在对石梁和石楼板加固的过程中对石材本身造成损伤，张世江等^[24]开展CFRP筋增强板加固石梁的受弯性能试验研究，对比了不同配筋率以及石梁与CFRP筋增强板之间的界面粗糙程度对加固石梁承载能力的提升效果。叶勇等^[25]研究了预制CFRP筋增强板加固石板的抗弯承载能力，将其与表层嵌埋CFRP筋加固技术进行对比，结果表明：前者的抗弯性能更强且加固过程更为简单。

综合上述研究，目前针对石材受弯构件所提出的加固技术均能优化其抗弯能力。然而，面对既有石结构民房加固时仍存在加固流程复杂、操作不便、破坏石材本身等问题。本文提出采用CFRP板对既有石楼板进行抗弯加固，通过在石楼板底部受拉区粘贴CFRP板与石板协同受力，从而实现其抗弯性能的提升。该技术减少了对石板开槽、打孔以及对CFRP板的预应力张拉和锚固等操作流程，避免了对石板造成损伤同时也保证了施工便捷与造价可控，利于针对大量既有石结构民宅加固。为此，本文开展CFRP板加固既有石楼板的抗弯性能试验，对比采用不同厚度和宽度的CFRP板加固对既有石楼板抗弯性能的影响，旨在为石材结构加固的工程实践和技术创新提供科学的理论支持。

1   试验概况

1.1   试验设计及制作

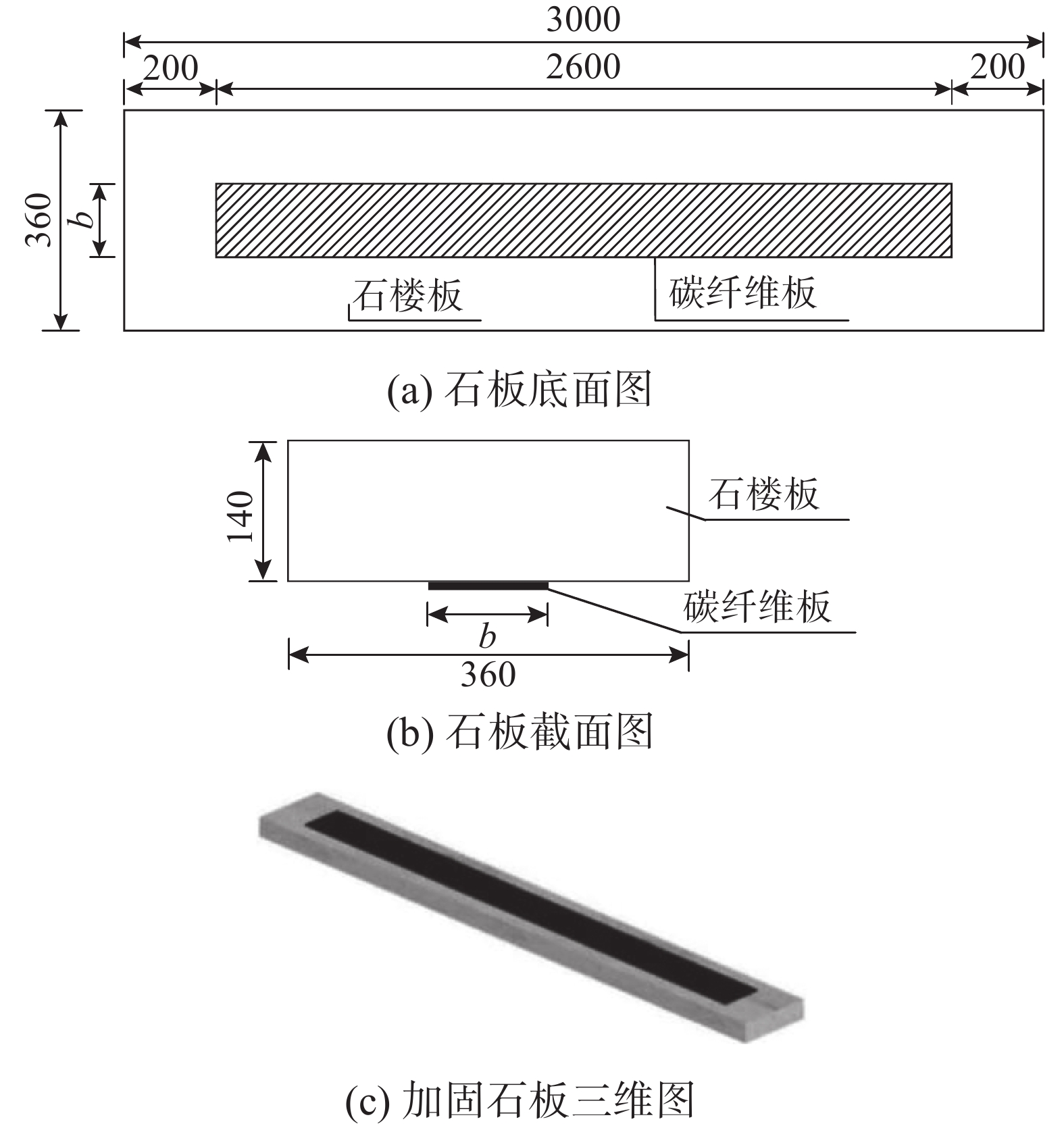
为验证CFRP板加固技术的可行性，本次试验共设计制作5个CFRP板加固石板和1个未加固石板。试件编号及参数见表1，试件构造及石板尺寸如图2所示。考虑到试验研究内容是对既有石结构石楼板进行加固，为了确保试验研究的准确性，并尽可能地模拟目标加固环境，本次试验所使用的石楼板均从已建成的石结构建筑中拆除而得。根据《纤维增强复合材料建设工程应用技术规范》(GB 50608−2010)^[26]CFRP板粘贴长度宜延伸至支座边缘，加固时采用CFRP板粘贴长度均为2600 mm。试验以CFRP板厚度和宽度作为参数变量，研究CFRP板厚度和宽度对石板承载能力、破坏形态、变形性能等的影响。

表  1  石楼板加固参数

Table  1.  Reinforcement parameters of stone floor slab

试件编号	试件尺寸 长×宽×高/mm	CFRP板
		数量/片	宽度/mm	厚度/mm
S-W1	3000×360×140	−	−	−
S-C-W2	3000×360×140	1	100	1.2
S-C-W3	3000×360×140	1	100	2.0
S-C-W4	3000×360×140	1	100	3.0
S-C-W5	3000×360×140	1	80	2.0
S-C-W6	3000×360×140	1	60	2.0

下载: 导出CSV 

| 显示表格

图  2  CFRP板加固石楼板构造及几何尺寸 /mm

Figure  2.  Structure and geometric dimensions of carbon fiber reinforced concrete slabs

下载: 全尺寸图片 幻灯片

石楼板试件均产于福建省泉州市惠安县，为获得试验石板的材料基本性能，根据ASTM D3967-16^[27]和ASTM C170/C170M-17^[28]的规范，分别对石材的抗拉强度和抗压强度进行了测定，所有试件均处于自然干燥状态，因此未考虑石材含水量对其抗拉和抗压性能的影响。在劈裂抗拉试验中，选用了两组各6个直径分别为50 mm和60 mm、高径比为1的试样。对于轴向压缩试验，则制备了两组各6个圆柱形试样，直径同样为50 mm和60 mm，高径比为1，以评估石材的抗压强度和弹性模量；结果表明：该批石材的抗劈裂强度平均值为8.71 MPa，轴向抗压强度平均值为108.42 MPa，弹性模量为45 GPa，CFRP板及碳板胶力学实测性能见表2。

表  2  CFRP板及碳板胶力学性能

Table  2.  Mechanical properties of carbon fiber board and carbon board adhesive

材料	抗拉强度/ MPa	受拉弹性 模量/MPa	伸长率/(%)	抗压强度/ MPa
CFRP板	2422.71	1.7×105	1.63	−
CFRP-A/B胶	49.21	4543.89	1.64	121.27

下载: 导出CSV 

| 显示表格

本次试验粘贴CFRP板加固石楼板的加固过程为：① 用角磨机对石板粘贴位置打磨平滑(图3(a))，针对局部缺陷采用找平胶厚涂对石板进行修补；② 将A、B两组碳板胶按2∶1倒入容器内，按同一方向将其完全调匀，翻看容器底部的颜色，确保配好的胶体色泽一致；③ 对石板粘贴区域厚涂一层底胶，用刮刀用力反复涂刷，使胶能均匀地粘附在石板表面；④ 将碳板胶以中间厚边缘薄形式涂在CFRP板粘贴面上(图3(b))，然后将CFRP板贴合于石板底部。利用刮刀将边缘溢出胶粘剂由外向内刮抹、挤压(图3(c))，除去板缝之间的孔隙和气泡，确保石板加固面与CFRP板紧密接触，最后在CFRP板表面施加重物对其进行加压，保证CFRP板的粘接效果(图3(d))。

图  3  CFRP加固石板制作过程

Figure  3.  Manufacturing process of CFRP reinforced stone slab

下载: 全尺寸图片 幻灯片

1.2   加载装置及加载制度

试验加载装置如图4所示，试验采用四点弯曲加载法，利用千斤顶通过分配梁来施加荷载，荷载作用点位于净跨(${l_0} = 2700 \;{\rm{mm}}$)的三等分位置。通过分配梁，荷载均匀地传递至加载点。为了实现简支梁的边界条件，石楼板的两端分别采用固定和滑动的铰接支座。为避免应力集中效应，在加载点和支座处安置钢板。并在试件下方设置垫梁保护加载场地。

在正式加载之前，试验需进行多次预加载，确保正式试验的正顺利进行。本次试验采用力-位移混合控制方式进行加载。试件发生开裂之前，试验采用荷载控制方式，每级荷载增加2 kN，以收集石楼板开裂前的性能数据；当石楼板开裂以后，转换为位移控制方式，每级位移增加1 mm，继续加载直至试件破坏。每一级加载后保持2 min，以便记录和观察裂缝的情况。

图  4  试验加载装置

Figure  4.  Test loading device

下载: 全尺寸图片 幻灯片

1.3   测点布置

试验的测量内容包括石板跨中应变、CFRP板应变、试件的挠度变化以及裂缝的发展规律。为监测加载过程中的挠曲变形，在石楼板的跨中、加载点和支座位置安装了共计5个电子位移计。此外，为测量石板跨中截面不同位置的石材应变，在跨中石板板侧沿石楼板厚度粘贴了9个应变片；为测量石板顶面和底面的应变，在石楼板跨中的板顶与板底位置，各粘贴了2个应变片。同时，沿CFRP板的长度方向，均匀粘贴了10个应变片，专门用于监测CFRP板应变的变化趋势。具体测点布置如图5所示。

图  5  试件测点布置 /mm

Figure  5.  Arrangement of measuring points of test piece

下载: 全尺寸图片 幻灯片

2   试验现象及其结果分析

2.1   试验现象及破坏形态

未加固石板S-W1的破坏形式表现为典型的脆性破坏。在石板开裂之前，荷载与挠度呈现出近似线性的关系增长。当石楼板出现裂缝后，裂缝迅速扩展发生脆性断裂。最终的断裂截面总体垂直于石楼板的底面(图6)。

图  6  未加固石楼板破坏形态

Figure  6.  Final failure mode of unreinforced slab

下载: 全尺寸图片 幻灯片

CFRP板加固厚度及宽度较小试件S-C-W2、S-C-W5和S-C-W6的破坏过程和最终破坏形态类似。加载初期，荷载与跨中挠度大致呈现直线上升的趋势。然而，当石楼板板底发生开裂(图7(a))时，荷载会迅速下降，下降幅度约为开裂荷载的30%。裂缝出现在石板跨中附近板侧受拉区边缘，开裂后裂缝沿石板厚度向板顶受压区发展，同时于石板底部由外向内延伸形成横向贯通裂缝(图7(b))，初始裂缝发展高度范围在80 mm~100 mm，宽度约为2 mm~3 mm。此时试件底部石材退出工作，荷载将由CFRP板承担。对比未加固石楼板S-W1，加固试件开裂后仍具有承载能力，随着荷载的增大，试件挠度增长加快，裂缝逐渐扩宽且沿着板厚向板顶受压区延伸。在此过程中，CFRP板开始由开裂处朝两侧支座剥离(图7(c))，剥离过程中CFRP板始终保持紧绷状态，直至碳板完全剥离，构件断裂坍塌(图7(d))，在此过程中未发现其他裂缝。试件破坏模式虽然属于跨中弯曲裂缝引起的CFRP板剥离破坏，但是在剥离破坏发生时，跨中平均挠度已超过了石板净跨${l_0}$的1/88，在破坏前具有一定预兆，为具有一定变形能力的弯曲破坏。

图  7  试件破坏过程及破坏形态

Figure  7.  Failure process and failure form of test pieces

下载: 全尺寸图片 幻灯片

对于CFRP板加固厚度和宽度较大试件S-C-W3和S-C-W4破坏过程和破坏形态类似。加载初期，荷载与跨中挠度呈线性增长，直至石板产生裂缝，荷载下降幅度仅为开裂荷载的10%。初始裂缝发展高度范围在30 mm~50 mm，裂缝宽度约为0.2 mm~0.4 mm。随着荷载的继续增加，荷载随着跨中挠度的增大呈锯齿状波动上升，在此过程中石板纯弯段相继产生开展了Y2、Y3等弯曲裂缝以及少量次生裂缝(图8(a))，裂缝发展方向与板底几乎垂直。初始裂缝Y1沿石楼板高度逐渐向上部受压区延伸，裂缝宽度也随之向两边拓展，CFRP板开始朝两侧支座剥离，整体拉应变也显著上升。当CFRP板完全剥离时，加载点附近裂缝贯通石板，构件断裂倒塌(图8(b))，破坏前跨中平均挠度达到板计算跨度的1/122，具有一定预兆，为变形能力良好的弯曲破坏。

图  8  试件破坏过程与破坏形态

Figure  8.  Failure process and failure morphology of test pieces

下载: 全尺寸图片 幻灯片

相比较素石板S-W1的脆性破坏，CFRP板加固试件破坏前均发生了显著变形，说明CFRP板加固可显著改善石楼板的脆性破坏形态，增强了石楼板的抗弯性能。与试件S-C-W2、S-C-W5、S-C-W6相比，试件S-C-W3、S-C-W4在破坏过程中主裂缝宽度较小，次生裂缝的发展速度相对比较缓慢。相比之下，次生裂缝的数量更为丰富，其分布也更加均匀。这表明：CFRP板阻碍了石楼板板底石材的裂缝发展，使试件整体受力更加均衡，从而推迟裂缝的产生。此外，CFRP板的厚度和宽度的增加，将逐步提高加固效果。

2.2   荷载-跨中挠度关系及受弯承载力

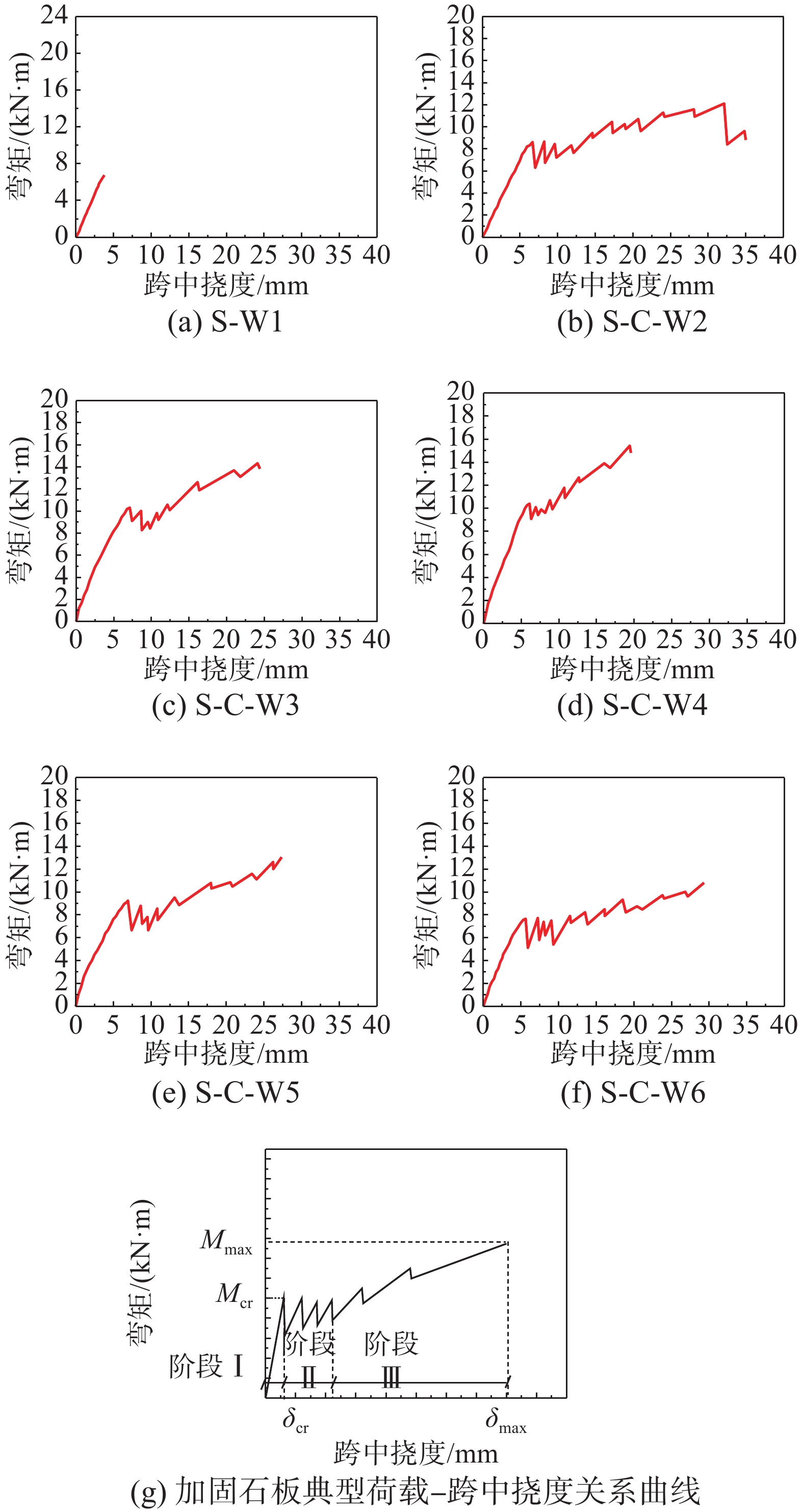
各试件主要试验结果列于表3，荷载-跨中挠度关系如图9所示。由图9中可以观察到，未经过加固的石板S-W1的荷载-挠度曲线大致呈线性关系，在断裂破坏之前，弯曲变形并不显著，仅为3.78 mm，约为净跨${l_0}$的1/714，其破坏形式表现为为典型的脆性破坏。而CFRP板加固试件的荷载-挠度曲线均呈现锯齿波动上升发展趋势，典型CFRP板加固试件荷载-跨中挠度曲线如图9(g)主要呈现三个阶段发展：① 弹性工作阶段，此阶段为试件加载初期到纯弯段出现第一条裂缝，荷载-挠度曲线关系呈近似直线增长，在此期间，CFRP板变形较小且未发生剥离；② 裂缝发展阶段，此阶段为石楼板首次开裂到纯弯段裂缝发展稳定。在此过程中，荷载-挠度曲线呈现锯齿形上下波动，这是由于花岗岩石材的抗拉强度较高，在石板开裂时，原本由受拉区石材承担的荷载将传递至CFRP板。为了抵抗这些荷载，CFRP板需发生一定程度的变形，因此荷载出现上下波动，而荷载的每次骤降对应裂缝的产生及发展；③ 上升阶段，纯弯段裂缝发展稳定后，试件荷载-挠度曲线表现出锯齿形波动上升规律，曲线上升斜率低于弹性工作阶段，整体起伏稳定，基本保持稳定增长。

表  3  各试件主要试验结果

Table  3.  Main experimental results of specimens

试件编号	Mcr/ (kN·m)	δcr/ mm	acr/ (%)	Mmax/ (kN·m)	δmax/ mm	amax/ (%)	δmax/l0	md
S-W1	6.75	3.78	−	6.75	3.78	−	1/714	1.00
S-C-W2	8.62	6.66	27.7	12.11	34.99	79.41	1/77	5.25
S-C-W3	10.30	7.12	52.59	14.33	24.41	112.29	1/110	3.43
S-C-W4	10.40	6.10	54.07	15.43	19.56	128.59	1/139	3.21
S-C-W5	9.23	6.93	36.74	13.05	27.35	93.33	1/99	3.95
S-C-W6	7.65	5.62	13.33	10.81	29.32	60.15	1/92	5.22
注：${M_{\rm cr}}$、${M_{\max }}$为开裂弯矩以及最大弯矩 ；${\delta _{\rm cr}}$、${\delta _{\max }}$为两种状对应于的跨中挠度；${a_{\rm cr} }$、${a_{\max }}$分别为开裂弯矩、极限弯矩相对未加固石板提高的百分比；${m_{\rm d}}$为延性系数，${m_{\rm d}} = {\delta _{\max }}/{\delta _{\rm cr}}$。

下载: 导出CSV 

| 显示表格

对比未加固试件，CFRP板加固试件的破坏形式由不明显变形的脆性破坏转变为具有一定变形能力的弯曲破坏性形态，加固试件的极限变形达到净跨${l_0}$的1/139~1/77。石板试件的延性系数${m_{\rm d}}$定义为极限挠度${\delta _{\max }}$与开裂挠度${\delta _{\rm cr}}$之比，结果如表3所示，可见CFRP板加固试件的变形能力较好。根据图9所示，在同一水平的荷载作用下，各试件之间的跨中挠度表现出一定规律，随着加固时采用CFRP板的厚度和宽度的增大，石楼板跨中的变形逐渐减小。说明试件整体的抗弯刚度与其采用CFRP板的加固参数有关，增加CFRP板的厚度和宽度在一定程度上能够提高加固试件整体的抗弯刚度，这一结果与已有的研究^[29]相符。

此外，CFRP板能够抑制石楼板跨中板底肉眼不可见的微小裂缝，防止其进一步发展，从而提高了石板的开裂荷载和开裂时的跨中挠度。对比图9(b)、图9(d)、图9(f)、图9(c)，试件S-C-W2、S-C-W4、S-C-W6、S-C-W3开裂荷载较未加固石板分别提升了27.7%、54.07%和13.33%、52.59%，表明：随着CFRP板厚度和宽度增大，对裂缝的抑制效果更加显著。同时，随着CFRP板厚度和宽度的增大，开裂时荷载-挠度曲线的波动程度有所降低，相比试件S-C-W2、试件S-C-W6开裂时荷载下降的幅度29.41%和33.19%，试件S-C-W4、试件S-C-W3开裂时荷载降幅仅为10%左右。这是因为，随着CFRP板的厚度和宽度增大，其在承受原本由石材所承受的拉力时产生的变形量会减少，这导致荷载变化的幅度也随之降低。

图  9  试件荷载-跨中挠度关系

Figure  9.  Relationship between load and mid span deflection of test piece

下载: 全尺寸图片 幻灯片

素石板开裂荷载即为极限荷载，而CFRP板加固后的石楼板在石板开裂后仍然能够承担荷载。其中试件S-C-W2、S-C-W6的极限荷载较试件S-W1分别提升了79.41%和60.15%，开裂后荷载-挠度曲线较为平缓；随着CFRP板的厚度和宽度增大，试件S-C-W4、S-C-W3的极限荷载较S-W1分别提升了128.59%和112.26%，开裂后的荷载-挠度曲线呈现出明显上升阶段。这是由于：开裂前，荷载主要由石板自身承担，CFRP板处于低水平应力状态；开裂后，石材退出工作，板底拉力全部由CFRP板承担，因此CFRP板加固厚度和宽度越大的试件可以抵抗更大的极限荷载。由此可见，采用CFRP板加固技术能够有效改善未加固石板的脆断性能，提高石板的抗弯承载力以及变形能力。

2.3   纯弯段石材应变变化规律

通常情况下，位于石楼板跨中部分板顶位置处的石材的压应变最大，而位于石楼板跨中部分板底位置的石材拉应变最大。不同宽度和厚度的CFRP板加固石楼板在开裂前，石板跨中表面测得最大拉、压应变列于表4。与文献[15]所描述的情况相同，CFRP板加固石板在开裂前跨中最大拉、压应变显著增大，采用不同参数CFRP板加固的石楼板(S-C-W2~S-C-W6)在开裂前的最大拉应变较未加固试件S-W1均提高了66.92%以上。此外，随着CFRP板的厚度、宽度的增加，石材极限拉应变也随之提高。这说明采用CFRP板加固石楼板能延缓受拉区石材的裂缝发展，使石板整体受力更加均匀，从而延缓裂缝的形成，提高石板开裂荷载。

表  4  开裂前石楼板最大拉、压应变

Table  4.  Maximum tensile and compressive strain of stone slab before cracking

试件编号	最大压 应变${\varepsilon _{ {\rm c}\max } }/{\text{με} }$	最大拉 应变${\varepsilon _{ {\rm t}\max } }/{\text{με} }$	${\alpha _{{\rm t}\max } }$/(%)
S-W1	219.13	237.32	−
S-C-W2	326.97	396.14	66.92
S-C-W3	364.90	507.06	113.66
S-C-W4	503.40	682.24	187.48
S-C-W5	381.46	477.38	101.15
S-C-W6	331.21	407.95	71.89
注：${\alpha _{{\rm t}\max } }$为加固石楼板的最大拉应变相对未加固石板最大拉应变的提高幅度。

下载: 导出CSV 

| 显示表格

石楼板开裂前，不同厚度和宽度的CFRP板加固石板跨中截面石材应变以及CFRP板应变与荷载关系如图10所示，素石板与CFRP板加固石板在跨中截面上的应变分布以及跨中截面应变的整体发展规律完全一致，均符合平截面假定的要求。从图10(b)~图10(f)可以看出，不同加固厚度和宽度的CFRP板与石楼板之间展现出良好的工作性能。同一位置处的CFRP板与石材应变相近，表明在石楼板开裂之前，石楼板与CFRP板的粘结性能良好，两者变形协调。

特别需要指出的是，在石板的弯曲过程中，中性轴出现了显著的位移。在初始加载阶段，石板跨中的截面中性轴大致与截面的对称轴对齐，中性轴处的应变沿石板的高度呈线性分布。然而，随着荷载的逐步增加，中性轴逐渐向板顶的受压区偏移。临近石楼板开裂时，中性轴大约已经向板顶受压区移动了5 mm~10 mm。这是由于花岗岩石材是一种脆性材料，其抗压强度高于抗拉强度，受拉弹性模量E_t低于受压弹性模量E_c。在对花岗岩石楼板施加荷载产生弯矩时，为了满足截面受力平衡，需要额外的受拉区面积产生的拉力与受压区的压力相互平衡。随着荷载不断增大，石楼板的受拉区会逐渐产生对于人眼不可见的细微裂缝，这些裂缝对石板造成影响使得石材受拉弹性模量E_t进一步降低，最终导跨中石材截面中性轴朝板顶偏移。

图  10  石楼板跨中截面应变分布

Figure  10.  Strain distribution of mid span section of stone slab

下载: 全尺寸图片 幻灯片

2.4   CFRP板应变分布及其发展规律

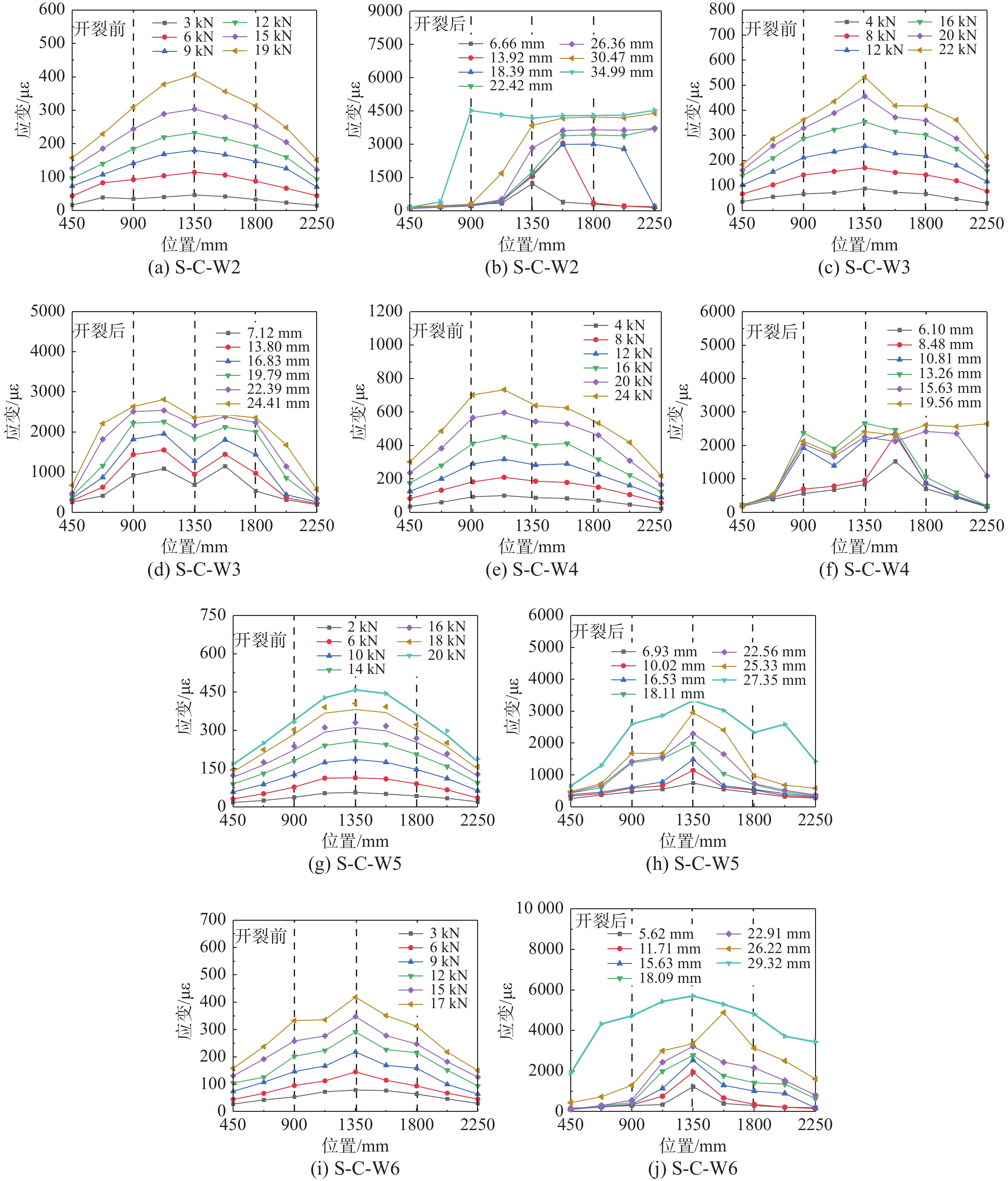
在不同荷载作用下，加固试件CFRP板应变分布及发展如图11所示。图11按照试件的受损情况(石楼板开裂前和石楼板开裂后)将CFRP板的应变分布划分为两个阶段，纵向的三根虚线分别表示CFRP板加固试件的加载点及跨中位置。从图11分析可以得知，在裂缝形成前，CFRP板与石楼板共同承担荷载，试件的应变分布特征表现为中间区域拉应变较高，而两端拉应变较低。拉应变的最大值通常出现在石板的中部，而在支座的两端，应变值几乎为零。此时，CFRP板的整体应变处于较低水平。这是因为在开裂前，石板本身承受荷载，CFRP板的受拉程度相对较低。随着荷载的不断增加，CFRP板的应变与石楼板一起逐渐增大，然而应变的分布依然显示出从中点向两端逐渐降低的模式，这反映了试件在各个位置上荷载分布的特点。说明在石楼板发生开裂之前，CFRP板与石楼板之间实现了协同承担荷载，并没有出现两者之间相对滑动的现象。

图  11  CFRP板应变分布

Figure  11.  Strain distribution of CFRP

下载: 全尺寸图片 幻灯片

裂缝产生以后，石板失去抗拉能力，原本石板承受的拉力将转移至CFRP板，导致CFRP板拉应变迅速增大。结合2.1节试验现象中的裂缝分布可知，对于试件S-C-W2、S-C-W5、S-C-W6，开裂后纯弯段仅产生单一裂缝，开裂处CFRP板承担全部受拉作用，应变增幅剧烈，在图11(b)、图11(h)、图11(k)中有明显凸起。继续加载，CFRP板以开裂处为起点向左、右两侧剥离，相应的剥离位置CFRP板应变也迅速增大，而未开裂截面碳纤板并未发生明显剥离，拉应变保持原有低应变水平。对于试件S-C-W3、S-C-W4，纯弯段裂缝数量多，裂缝发展高度低，CFRP板整体应变发展均匀，未发生应力集中现象。

加载后期，加固试件S-C-W6的CFRP板最大应变达接近6000 με，而试件S-C-W4的CFRP板最大应变约为2500 με，这说明：截面面积较小的CFRP板能够更充分发挥CFRP板的材料性能，提高材料利用率。在图11(f)中出现了CFRP板应变减小的回弹现象，是因为试件S-C-W4出现了较多的裂缝，随着新裂缝的形成，CFRP 板在石楼板新开裂处开始共同承担拉力，从而缓解了原有的应力集中。这使得CFRP板整体应变应力达到了新的平衡状态。这一现象与已有的研究成果^[24]类似。

3   CFRP板加固石楼板承载力计算

3.1   基本假设

试验结果表明：素石板跨中板底一旦产生裂缝，裂缝将迅速贯穿石板跨中截面，发生脆性破坏。因此，素石板的开裂荷载即为其极限承载力。而对于采用CFRP板加固的石楼板，其承载能力的计算将采用另一种方法。在进行计算时，需满足以下基本假定：

1) CFRP板应力-应变关系采用线性模型^[30]，即：

式中，${\sigma _{\rm f}}$、${\varepsilon _{\rm f}}$、${E_{\rm f}}$分别为CFRP板的应力、应变和弹性模量。

2) 花岗岩石材的受压应力-应变关系，参考叶勇博士论文^[31]，石材临近极限压应变前呈线性关系，考虑计算方便，采用以下模型进行分析：

上升段： ${\sigma _{\rm{c}}} = {E_{\rm{s}}}{\varepsilon _{\rm{c}}},\qquad {\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{\rm{cu}}}$

下降段：

式中：${\sigma _{\rm{c}}}$、${\varepsilon _{\rm{c}}}$、${f_{\rm{sc}}}$分别为石材压应力、压应变和抗压强度；${E_{\rm{s}}}$为石材弹性模量，由于石材受拉和受压弹性模量较为接近，为方便计算则取统一值45 GPa；$\xi = {\varepsilon _{\rm{c}}}/{\varepsilon _{\rm{cu}}}$，${\varepsilon _{\rm{cu}}}$为石材极限应变，基于石材受压应力-应变曲线取为3000 με。

石材的受拉应力-应变关系采用线性模型，即：

破坏前：${\sigma _{\rm{t}}} = {E_{\rm{s}}}{\varepsilon _{\rm{t}}}, \qquad {\varepsilon _{\rm{t}}} \leqslant {f_{\rm{st}}}/{E_{\rm{s}}}$

破坏后：

式中，${\sigma _{\rm{t}}}$、${\varepsilon _{\rm{t}}}$、${f_{\rm{st}}}$分别为石材的受拉应力、应变和抗拉强度。不考虑石材的受拉塑性行为。

3) CFRP板和石楼板之间的粘结良好，两者之间的胶层厚度分布均匀，石材和CFRP板之间变形同步，未发现相对滑移现象^[32]。

4) CFRP板加固石板在加载的过程中，截面持续保持与轴线垂直状态。

5) CFRP板和石材的应变符合平截面假定。

3.2   开裂荷载和极限荷载计算

1) 未加固石楼板开裂弯矩计算

素石板在开裂前处于弹性工作阶段，荷载-位移曲线近似直线。当素石板接近开裂荷载时，截面中性轴向板顶发生了位移，但整体偏移量不大。为了简化计算，可以假设未加固石板破坏前，石板的中性轴仍位于截面对称轴上。基于这一假设，可以计算出未加固石板的开裂弯矩为：

式中：${f_{\rm st}}$为石材抗拉强度，由材性试验得${f_{\rm st}}$为8.71 MPa；$W$为抗弯截面系数，对于矩形截面$W = b{h^2}/6$，其中 $b$ 为截面宽度，$h$为截面高度。由于石板表面凹凸不平，计算时可偏安全地取$b = 340 \;{\rm{mm}}$、$h = 120 \;{\rm{mm}}$。

2) CFRP板加固石楼板开裂荷载计算

CFRP板加固石板开裂弯矩为石板所承受的弯矩加上CFRP板承受弯矩，计算简图如图12所示。

图  12  板底开裂时截面受力和变形情况

Figure  12.  Stress and deformation of the section when the plate bottom cracks

下载: 全尺寸图片 幻灯片

为简化计算过程，假定在裂缝形成时中性轴仍然位于截面对称轴上。根据试验结果分析，CFRP板能显著提升石楼板临近开裂时的最大拉应变，其最大应变提升幅度为66.92%~187.48%。这说明CFRP板不仅提高了石材利用效率，也增大了石楼板在开裂前的承载能力，即开裂荷载。因此，CFRP板加固石楼板开裂荷载公式为：

式中：${\beta _{\rm{C}}}$为基于CFRP板有效抑制受拉区石材裂缝发展而提高石材本身的材料发挥系数，与试验结果进行对比选取，保守取普通粘贴CFRP板的${\beta _{\rm{C}}} = 1.1$；$\varepsilon {}_{\rm{f}}$为CFRP板拉应变，根据试验取为石材开裂前平均最大拉应变$\varepsilon {}_{\rm{f}}$=500 με；${A_{\rm{f}}}$为CFRP板的截面面积；$h{}_{\rm{f}}$为CFRP板到截面受压区合力点距离，$h{}_{\rm{f}}$=105 mm。

采用式(5)进行计算得到未加固石板和CFRP板加固石板开裂荷载设计值与试验值对比如表5所示。

表  5  试件承载力计算值与试验值对比

Table  5.  Comparison between calculated value and test value of specimen bearing capacity

试件 编号	${\varepsilon _{\rm{f}}}{E_{\rm{f}}}{A_{\rm{f}}}{h_{\rm{f}}}$/ (kN·m)	${M_{\rm{cr,j}} }$/ (kN·m)	${M_{{\rm{cr,s}}} }$/ (kN·m)	${M_{\max,{\rm{j}}} }$/ (kN·m)	${M_{\max,{\rm{s}}} }$/ (kN·m)	${M_{\rm{cr,j}} }$/ ${M_{{\rm{cr,s}}} }$	${M_{\max,{\rm{j}}} }$/ ${M_{\max,{\rm{s}}} }$
S-W1	−	6.53	6.75	6.53	6.75	0.97	0.97
S-C-W2	1.76	8.29	8.62	10.97	12.11	0.96	0.91
S-C-W3	2.62	9.15	10.30	14.03	14.33	0.89	0.98
S-C-W4	3.43	9.96	10.40	16.95	15.43	0.96	1.09
S-C-W5	2.13	8.66	9.23	12.61	13.05	0.94	0.97
S-C-W6	1.76	8.29	7.65	10.97	10.81	1.08	1.01
注：${M_{\rm{cr,j}}}$、${M_{{\rm{cr,s}}}}$为开裂弯矩计算值与试验值 ；${M_{\max,{\rm{j}}}}$、${M_{\max,{\rm{s}}} }$为极限弯矩计算值和试验值。

下载: 导出CSV 

| 显示表格

3) CFRP板加固石楼板极限承载力计算

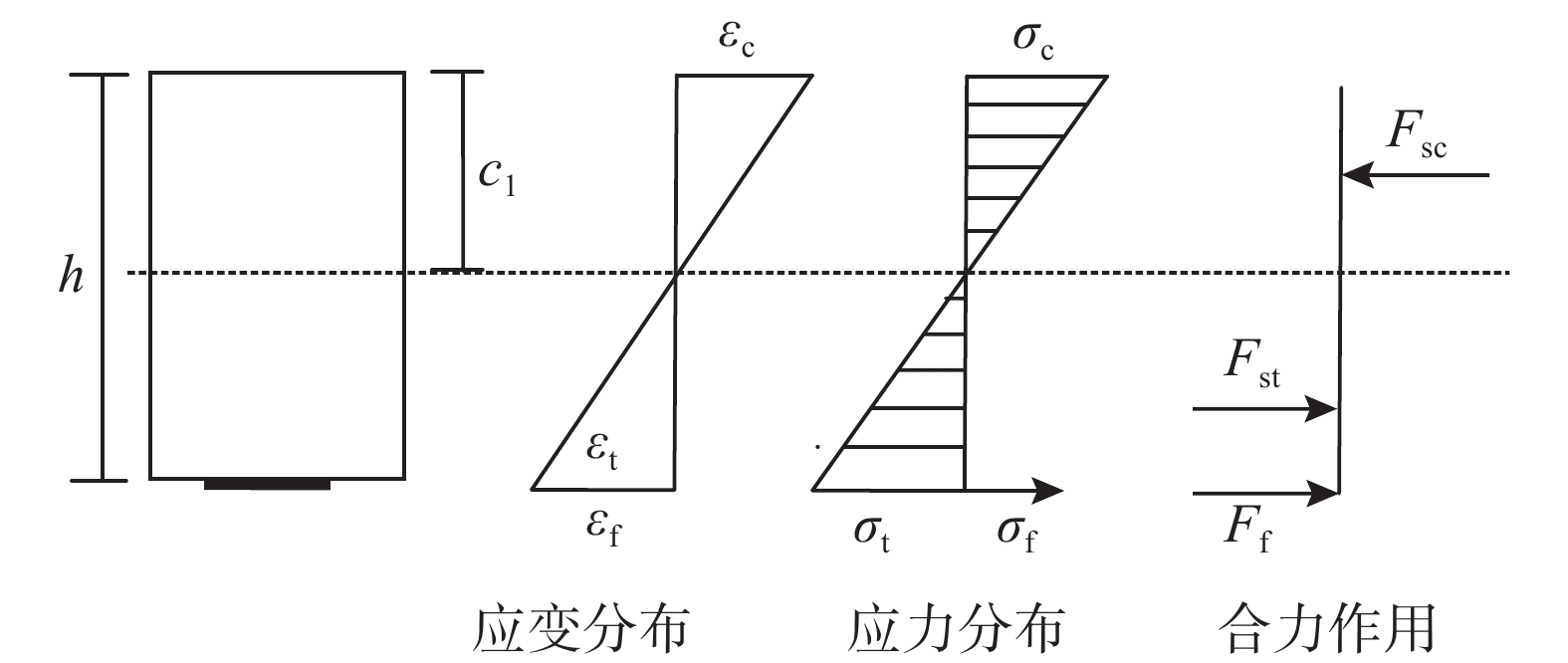
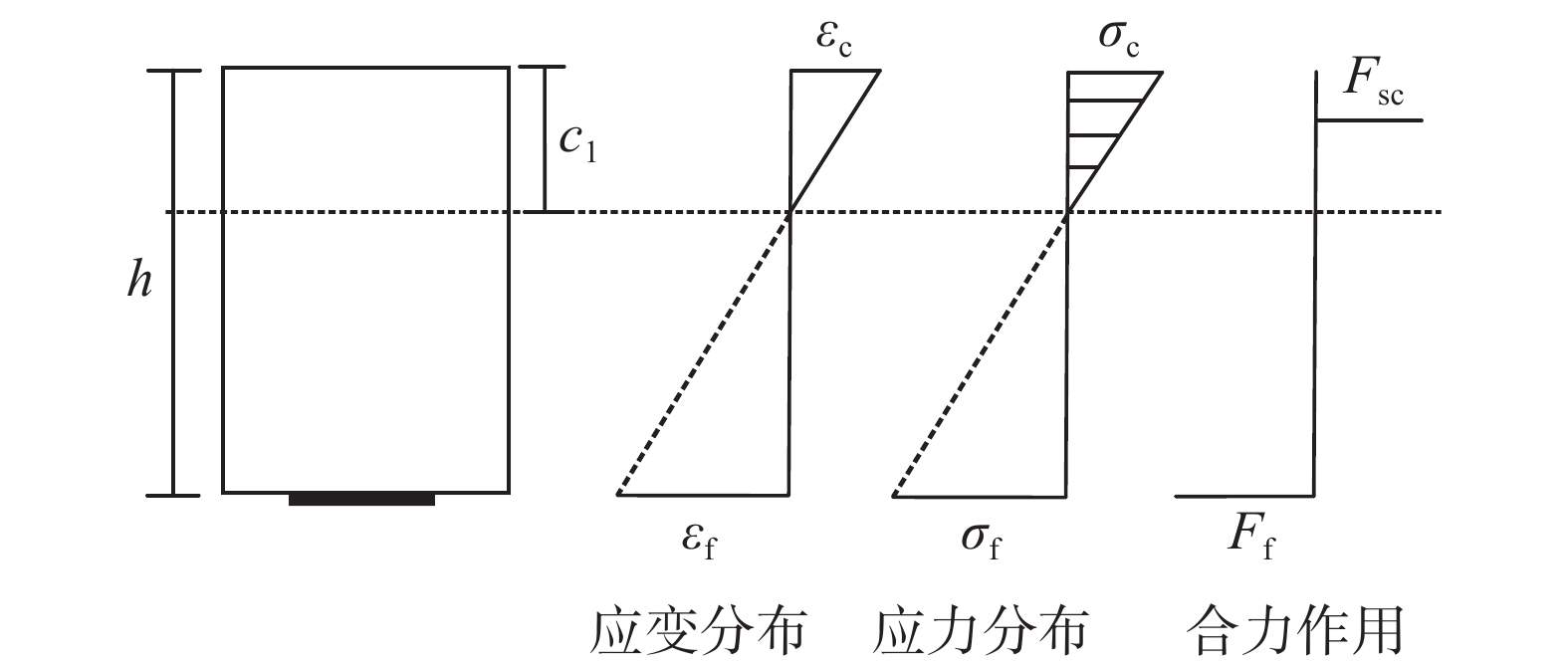
对于CFRP板加固石板，板底开裂后底部受拉区石材退出工作，计算截面简图如图13所示。

图  13  破坏时截面受力和变形情况

Figure  13.  Stress and deformation of section during failure

下载: 全尺寸图片 幻灯片

CFRP板加固石板达到极限荷载时，合力作用下的静力平衡条件为：

式中：${F_{\rm{sc}}}$为截面受压区石材合力；${F_{\rm{f}}}$为CFRP板拉力。${F_{\rm{sc}}}$和${F_{\rm{f}}}$可以按式(7)~式(8)计算：

式中：${\alpha _1}$和${\beta _1}$为石材等效矩形应力图系数，根据文献[31]分别取${\alpha _1}$=0.836，${\beta _1}$=0.694；$c_1$为石板受压区高度；${\varepsilon _{\rm{f}}}$为此时CFRP板的应变。截面的变形协调关系为：

将式(7)~式(9)代入式(6)，可得：

可以解得：

外部荷载作用下产生的弯矩${M_1}$为石板受压区和受拉区合力产生的弯矩，即：

由试验结果可得，CFRP板加固石板破坏时板顶石材平均应变为900 με左右。因此，实际加固设计时，可将${\varepsilon _{\rm{c}}}$=900 με代入式(12)进行极限受弯承载力计算。由于石板均为既有石结构房屋拆卸下来的既有石楼板，为考虑石楼板已有的损伤以及石材本身薄弱截面对承载力的影响，本文在计算的过程中引入承载力折减系数$\phi$^[33]，根据试验结果保守取$\phi$=0.455。素石板和不同宽度和厚度的CFRP板加固石板其承载能力计算值与试验值对比如表5所示。

由表5中的数据可以看出，理论计算值与试验所得开裂弯矩和极限弯矩的误差均不超过10%。两者匹配程度良好。CFRP板加固石板在石板跨中板底开裂之前，CFRP板承担的荷载较小，因此在计算开裂弯矩时，应主要考虑CFRP板对石材本身开裂时最大拉应变的提高效果。

4   结论

本文开展了CFRP板加固既有石楼板抗弯性能试验研究，根据试验和试验结果，得到以下结论：

(1) 采用粘贴CFRP板的方法对石楼板进行加固，可以显著改善其脆性破坏特征。加固后的石板在破坏前展现出一定的变形能力，表现为弯曲破坏。与未加固的石板相比，加固石板在破坏时的跨中挠度提高了358.2%以上。

(2) 粘贴CFRP板的加固方式能有效增强石楼板的抗弯承载能力。对于试件S-C-W2、S-C-W6、S-C-W3和S-C-W4，其极限荷载相较于未加固的石板S-W1分别提高了80%、60%、113.33%和126.67%，随着加固时采用CFRP板的厚度及宽度增大，加固效果更加显著。

(3) CFRP板通过阻碍跨中板底受拉区微裂缝的发展，从而提高石材的极限拉应变，进而提高石楼板的开裂弯矩。随着CFRP板的厚度和宽度增大，石材极限拉应变提升了66.92%~187.48%，开裂弯矩较素石板提升了13.33%~53.34%。

(4) 提出了CFRP板加固石楼板开裂弯矩和极限弯矩的计算公式，对实际石楼板加固具有一定的理论指导意义。