波浪往复流作用下沙纹床面的旋涡结构和悬沙运动数值研究

侯新妤; 陈鑫

doi:10.6052/j.issn.1000-4750.2022.08.0735

波浪往复流作用下沙纹床面的旋涡结构和悬沙运动数值研究

侯新妤^1,,
陈鑫^{1, 2, ,}

1.
中国农业大学水利与土木工程学院，北京 100083
2.
中国农业大学北京市供水管网系统安全与节能工程技术研究中心，北京 100083

基金项目: 国家自然科学基金项目(41961144014)

详细信息

作者简介:
侯新妤(1999−)，女，陕西人，硕士生，主要从事海岸泥沙研究(E-mail: houxinyu@cau.edu.cn)

通讯作者:
陈　鑫(1983−)，男，福建人，研究员，博士，博导，主要从事海岸泥沙研究(E-mail: chenx@cau.edu.cn)

中图分类号: TV142
计量
- 文章访问数: 146
- HTML全文浏览量: 20
- PDF下载量: 32
出版历程
- 收稿日期: 2022-08-23
- 修回日期: 2023-01-08
- 网络出版日期: 2023-02-20
- 刊出日期: 2024-10-24

A NUMERICAL STUDY ON VORTEX STRUCTURE AND SUSPENDED SEDIMENT MOVEMENT OVER RIPPLED BED IN WAVE-INDUCED OSCILLATORY FLOW

HOU Xin-yu^1,,
CHEN Xin^{1, 2, ,}

1.
College of Water Resources and Civil Engineering, China Agricultural University, Beijing 100083, China
2.
Beijing Engineering Research Center of Safety and Energy Saving Technology for Water Supply Network System, China Agricultural University, Beijing 100083, China

摘要

摘要:
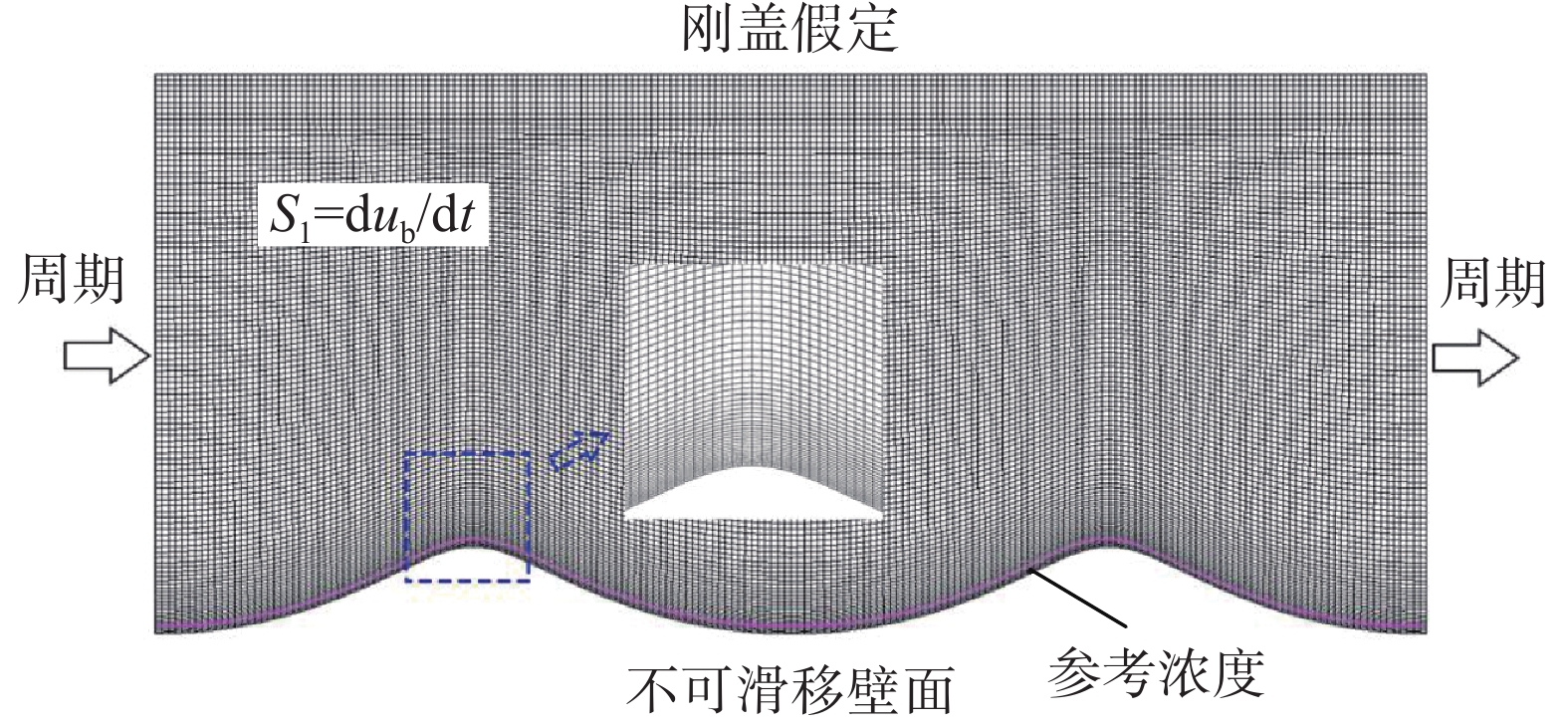
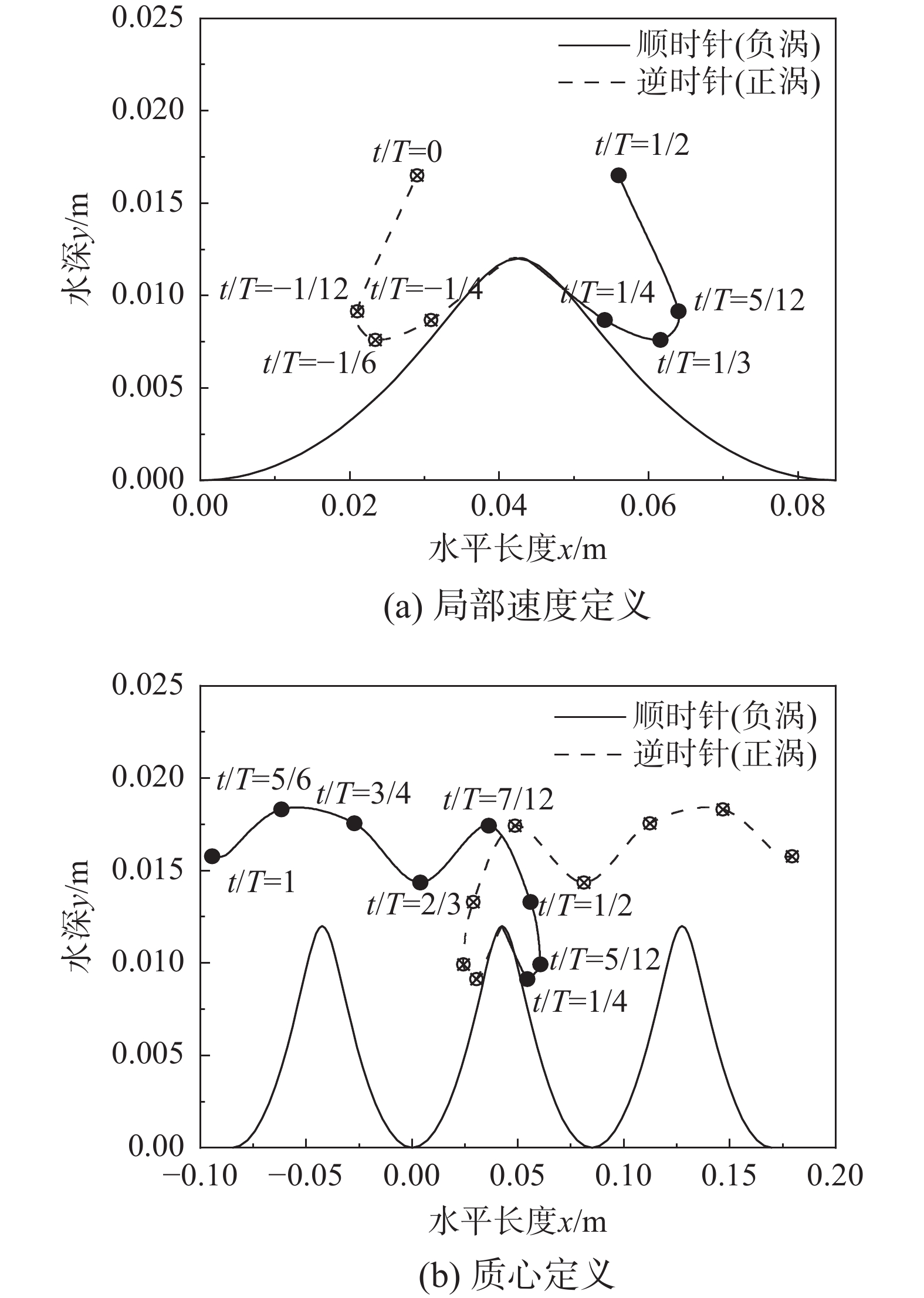
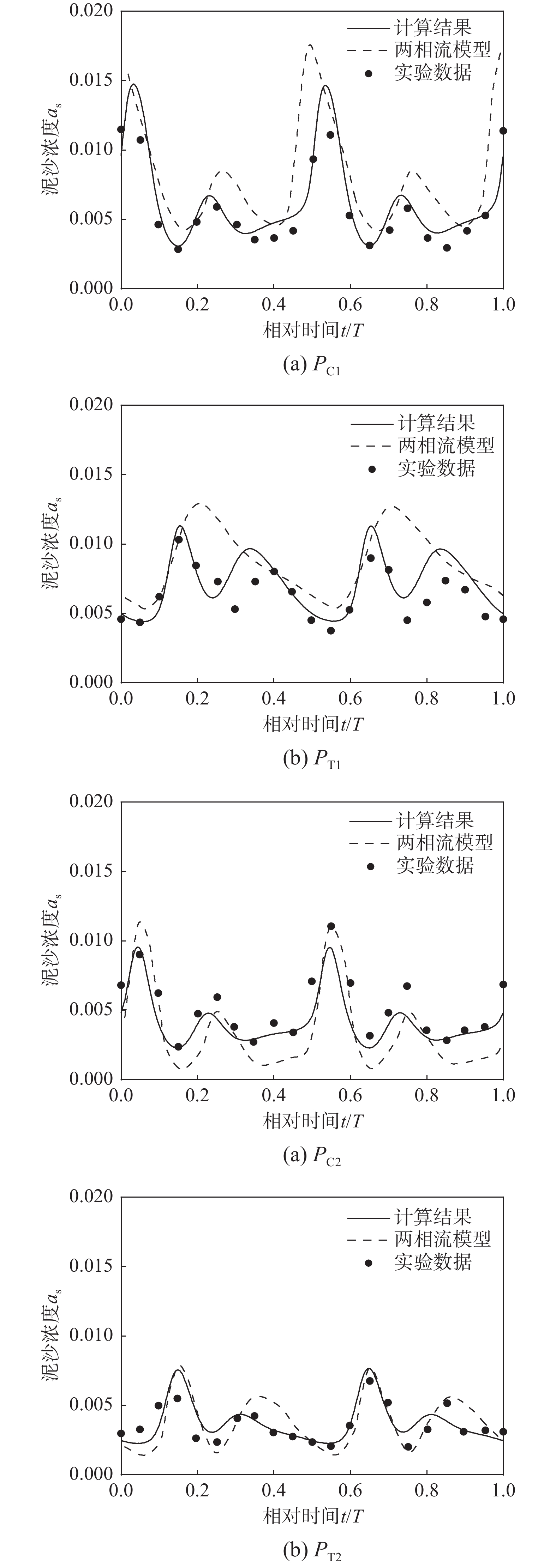
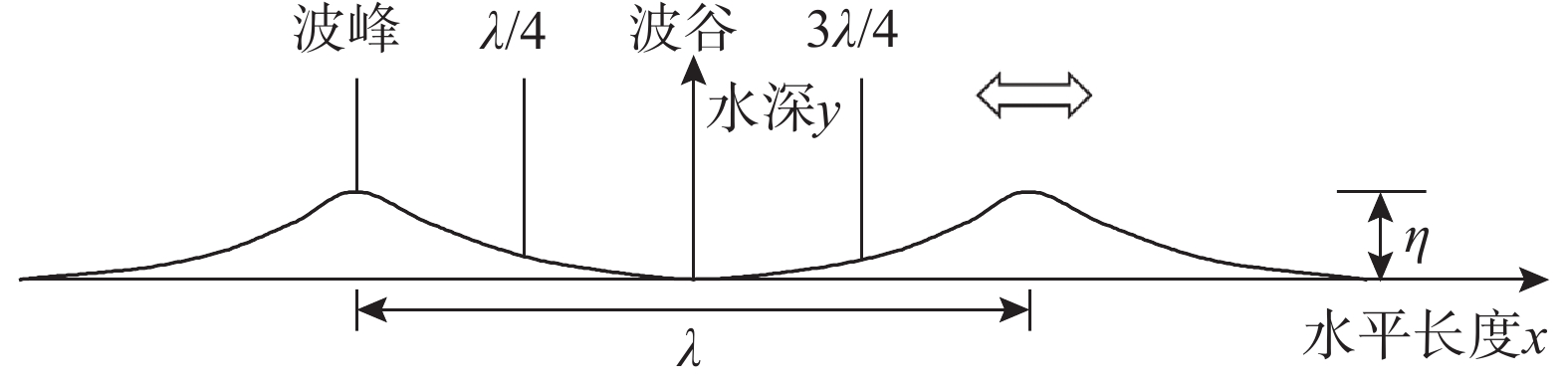
波浪作用下沙纹上的泥沙输运在海岸地貌的塑造中具有重要的地位，但相关的传统数值模型的精度受制于泥沙近底边界条件等因素。从最大程度节省计算成本且保证精度的角度考虑，该文发展了单相流的泥沙输移扩散数值模型以研究波浪往复流作用下沙纹床面的旋涡结构和悬沙运动。泥沙近底边界条件考虑了非线性波作用下的加速度效应和非对称边界层发展，以及泥沙的质量守恒和相位差效应。模型考虑了颗粒惯性及尾涡对泥沙运动的影响，同时以更适合沙纹上逆压梯度流的SST k-ω紊流模型闭合时均雷诺应力。数值结果与实验数据符合良好，可以准确预测沙纹固定点的周期浓度变化以及平均悬沙浓度在垂向上的分布。该文进一步选用边界截止涡量进行了涡中心、涡大小和涡强度的定量分析，用数值结果描述了旋涡的形成、发展和喷射过程以及对应的沙云团发展。
- 往复流 /
- 涡动沙纹 /
- 涡识别 /
- 颗粒尾涡 /
- 近底边界条件
Abstract:
Sediment transport above the rippled bed under wave motion plays an important role in coastal landforms, but the accuracy of traditional numerical models is limited by the bottom boundary condition for sediment behavior and oscillatory factors. In order to significantly save calculation cost and maintain accuracy, an advection-diffusion sediment numerical model of single-phase flow is developed to study the vortex structure and suspended sediment movement over rippled bed under wave-induced oscillatory flow. The bottom boundary condition for sediment takes into account the acceleration effect and asymmetric boundary layer development under nonlinear waves as well as the mass conservation and phase-lag of sediment. The effects of particle inertia and wake flow around sediment particle are considered, and the SST k-ω turbulence model which is more suitable for inverse pressure gradient flow over rippled bed is selected to close the time averaged Reynolds stress. The results of numerical model agree well with the experimental data and accurately predict the periodic concentration at fixed points and the vertical distribution of average suspended sediment concentration. The results define the cut-off vorticity level and quantitatively show the periodic development of vortex center, vortex size and vortex strength. Further results reproduce the formation, development and projection of the vortex and show the development of sediment cloud.
- oscillatory flow /
- vortex ripples /
- vortex identification /
- wake flow /
- bottom boundary condition

HTML全文

图 1 物理模型示意图

Figure 1. Schematic diagram of physical model

下载: 全尺寸图片幻灯片

图 2 参考浓度公式对比

Figure 2. Comparison of reference concentration formulae

下载: 全尺寸图片幻灯片

图 3 计算网格示意图

Figure 3. The mesh for simulation

下载: 全尺寸图片幻灯片

图 4 FREDSØE等^[3]实验不同位置水平流速模拟结果与实验数据对比图

Figure 4. Comparison of simulation results and experimental measurements of horizontal velocity at different locations in FREDSØE et al^[3] experiment

下载: 全尺寸图片幻灯片

图 5 NAKATO等^[38]实验周期流场模拟结果

Figure 5. Computed velocity in simulation of NAKATO et al^[38] experiment

下载: 全尺寸图片幻灯片

图 6 NAKATO等^[38]实验Q分布的模拟结果

Figure 6. Computed Q in simulation of NAKATO et al^[38] experiment

下载: 全尺寸图片幻灯片

图 7 模拟NAKATO等^[38]实验涡中心轨迹

Figure 7. Computed vortex center in simulation of NAKATO et al^[38] experiment

下载: 全尺寸图片幻灯片

图 8 模拟NAKATO等^[38]实验涡大小和涡强度周期变化

Figure 8. Computed vortex size and strength in simulation of NAKATO et al^[38] experiment

下载: 全尺寸图片幻灯片

图 9 不同边界截止涡量的结果对比

Figure 9. Comparison of different cut-off vorticity level

下载: 全尺寸图片幻灯片

图 10 NAKATO等^[38]实验不同相位悬沙浓度分布的模拟结果

Figure 10. Computed sediment volumetric concentration in simulation of NAKATO et al^[38] experiment

下载: 全尺寸图片幻灯片

图 11 NAKATO等^[38]实验波峰波谷上不同位置周期浓度的模拟结果与实验数据对比图

Figure 11. Comparison of simulation results and experimental measurements of volumetric sediment concentration at different locations above ripple crest and trough in NAKATO et al^[38] experiment

下载: 全尺寸图片幻灯片

图 12 平均悬沙浓度计算结果

Figure 12. Averaged sediment concentration

下载: 全尺寸图片幻灯片

表 1 沙纹实验的代表性参数

Table 1 Representative parameters of ripple experiment

工况作者	T/s	U_m/(m/s)	s_d	d_s/mm	λ/m	η/m	实验条件
NAKATO等^[38]	1.8	0.266	2.65	0.14	0.085	0.012	往复流水槽
RAMADAN^[39]	6.5	0.518	2.65	0.21	0.116	0.024	往复流水槽
FREDSØE等^[3]	2.5	0.255	−	−	0.220	0.035	波浪水槽
MAGAR等^[40]	7.5	0.689	2.65	0.35	0.567	0.078	往复流水槽
VAN DER WERF等^[41]	5.0	0.630	2.65	0.44	0.410	0.078	往复流水槽
注： T为周期；U_m为水质点速度极值；s_d为泥沙比重；d_s为泥沙粒径；λ为沙纹长度；η为沙纹高度。

下载: 导出CSV

参考文献(43)

[1]	BAGNOLD R A. Motion of waves in shallow water. Interaction between waves and sand bottoms [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1946, 187(1008): 1 − 18.
[2]	VAN DER WERF J J, MAGAR V, MALARKEY J, et al. 2DV modelling of sediment transport processes over full-scale ripples in regular asymmetric oscillatory flow [J]. Continental Shelf Research, 2008, 28(8): 1040 − 1056. doi: 10.1016/j.csr.2008.02.007
[3]	FREDSØE J, ANDERSEN K H, SUMER B M. Wave plus current over a ripple-covered bed [J]. Coastal Engineering, 1999, 38(4): 177 − 221. doi: 10.1016/S0378-3839(99)00047-2
[4]	BLONDEAUX P, VITTORI G. Vorticity dynamics in an oscillatory flow over a rippled bed [J]. Journal of Fluid Mechanics, 1991, 226: 257 − 289. doi: 10.1017/S0022112091002380
[5]	YUAN J, WANG D X. An experimental investigation of acceleration-skewed oscillatory flow over vortex ripples [J]. Journal of Geophysical Research: Oceans, 2019, 124(12): 9620 − 9643. doi: 10.1029/2019JC015487
[6]	EARNSHAW H C, GREATED C A. Dynamics of ripple bed vortices [J]. Experiments in Fluids, 1998, 25(3): 265 − 275. doi: 10.1007/s003480050229
[7]	MALARKEY J, DAVIES A G. Discrete vortex modelling of oscillatory flow over ripples [J]. Applied Ocean Research, 2002, 24(3): 127 − 145. doi: 10.1016/S0141-1187(02)00035-4
[8]	JESPERSEN T S, THOMASSEN J Q, ANDERSEN A, et al. Vortex dynamics around a solid ripple in an oscillatory flow [J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2004, 38(1): 127 − 138. doi: 10.1140/epjb/e2004-00108-y
[9]	CHEN X, YU X P. A numerical study on oscillatory flow-induced sediment motion over vortex ripples [J]. Journal of Physical Oceanography, 2015, 45(1): 228 − 246. doi: 10.1175/JPO-D-14-0031.1
[10]	刘传林, 韩新宇, 董胜. 半椭圆型防波堤水动力特性的数值模拟[J]. 工程力学, 2023, 40(10): 247 − 256. doi: 10.6052/j.issn.1000-4750.2022.01.0094 LIU Chuanlin, HAN Xinyu, DONG Sheng. Numerical simulation of hydrodynamic characteristics of semi-elliptic breakwater [J]. Engineering Mechanics, 2023, 40(10): 247 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.01.0094
[11]	张治国, 叶铜, 张成平, 等. 基于Pasternak海床模型的椭圆余弦波浪荷载作用下埋置管线动力响应解析解[J]. 工程力学, 2024, 41(1): 76 − 89. doi: 10.6052/j.issn.1000-4750.2022.02.0190 ZHANG Zhiguo, YE Tong, ZHANG Chengping, et al. Analytical solution for dynamic response of buried pipeline under cnoidal wave load based on Pasternak seabed model [J]. Engineering Mechanics, 2024, 41(1): 76 − 89. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.02.0190
[12]	陈林雅, 郑东生, 王盼娣, 等. 基于波浪-多孔介质海床-结构物耦合模型的单桩基础波浪力分析[J]. 工程力学, 2019, 36(11): 72 − 82. doi: 10.6052/j.issn.1000-4750.2018.08.0455 CHEN Linya, ZHENG Dongsheng, WANG Pandi, et al. Analysis of wave force acting on the monopile based on wave-porous seabed-structure coupled model [J]. Engineering Mechanics, 2019, 36(11): 72 − 82. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.08.0455
[13]	TROUW K, WILLIAMS J J, ROSE C P. Modelling sand resuspension by waves over a rippled bed [J]. Estuarine, Coastal and Shelf Science, 2000, 50(1): 143 − 151. doi: 10.1006/ecss.1999.0542
[14]	LI M, O'CONNOR B A. Numerical study of sediment transport above rippled beds under the action of combined waves and currents [J]. Sedimentology, 2007, 54(6): 1345 − 1363. doi: 10.1111/j.1365-3091.2007.00884.x
[15]	SISHAH B, VITTORI G. RANSE modeling of the oscillatory flow over two-dimensional rigid ripples [J]. Journal of Geophysical Research: Oceans, 2022, 127(1): e2021JC017439.
[16]	MALARKEY J, DAVIES A G. An eddy viscosity formulation for oscillatory flow over vortex ripples [J]. Journal of Geophysical Research: Oceans, 2004, 109(12): C12016. doi: 10.1029/2003JC002086
[17]	CHALMOUKIS I A, DIMAS A A, GRIGORIADIS D G E. Large-eddy simulation of turbulent oscillatory flow over three-dimensional transient vortex ripple geometries in quasi-equilibrium [J]. Journal of Geophysical Research: Earth Surface, 2020, 125(8): e2019JF005451.
[18]	JIN C, COCO G, TINOCO R O, et al. High-resolution large eddy simulations of vortex dynamics over ripple defects under oscillatory flow [J]. Journal of Geophysical Research: Earth Surface, 2022, 127(3): e2021JF006328.
[19]	BHAGANAGAR K, HSU T J. Direct numerical simulations of flow over two-dimensional and three-dimensional ripples and implication to sediment transport: Steady flow [J]. Coastal Engineering, 2009, 56(3): 320 − 331. doi: 10.1016/j.coastaleng.2008.09.010
[20]	MAZZUOLI M, KIDANEMARIAM A G, UHLMANN M. Direct numerical simulations of ripples in an oscillatory flow [J]. Journal of Fluid Mechanics, 2019, 863: 572 − 600. doi: 10.1017/jfm.2018.1005
[21]	CHANG Y S, PARK Y G. Suspension of sediment particles over a ripple due to turbulent convection under unsteady flow conditions [J]. Ocean Science Journal, 2016, 51(1): 127 − 135. doi: 10.1007/s12601-016-0011-2
[22]	FINN J R, LI M, APTE S V. Euler-lagrange simulations of sediment transport in oscillatory boundary layers with bedforms [J]. Coastal Engineering Proceedings, 2014, 1(34): 80 − 90.
[23]	何康, 施华斌, 余锡平. 基于两相流理论的稀疏和致密颗粒流统一模型[J]. 工程力学, 2023, 40(8): 24 − 35, 46. doi: 10.6052/j.issn.1000-4750.2021.12.0978 HE Kang, SHI Huabin, YU Xiping. The unified model for dilute and dense granular flows based on the two-phase flow theory [J]. Engineering Mechanics, 2023, 40(8): 24 − 35, 46. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.12.0978
[24]	ZYSERMAN J A, FREDSØE J. Data analysis of bed concentration of suspended sediment [J]. Journal of Hydraulic Engineering, 1994, 120(9): 1021 − 1042. doi: 10.1061/(ASCE)0733-9429(1994)120:9(1021)
[25]	ENGELUND F, FREDSØE J. A sediment transport model for straight alluvial channels [J]. Hydrology Research, 1976, 7(5): 293 − 306. doi: 10.2166/nh.1976.0019
[26]	CHEN X, NIU X J, YU X P. Near-bed sediment condition in oscillatory sheet flows [J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2013, 139(5): 393 − 403. doi: 10.1061/(ASCE)WW.1943-5460.0000193
[27]	CHEN X, LI Y, WANG F J. Mobile bed thickness in skewed asymmetric oscillatory sheet flows [J]. Acta Mechanica Sinica, 2018, 34(2): 257 − 265. doi: 10.1007/s10409-017-0686-3
[28]	SHI H B, YU X P. An effective Euler-Lagrange model for suspended sediment transport by open channel flows [J]. International Journal of Sediment Research, 2015, 30(4): 361 − 370. doi: 10.1016/j.ijsrc.2015.03.012
[29]	GREIMANN B P, MUSTE M, HOLLY JR F M. Two-phase formulation of suspended sediment transport [J]. Journal of Hydraulic Research, 1999, 37(4): 479 − 500. doi: 10.1080/00221686.1999.9628264
[30]	O'DONOGHUE T, WRIGHT S. Concentrations in oscillatory sheet flow for well sorted and graded sands [J]. Coastal Engineering, 2004, 50(3): 117 − 138. doi: 10.1016/j.coastaleng.2003.09.004
[31]	LI J X, CHEN X. A general two-phase mixture model for sediment-laden flow in open channel [J]. Journal of Hydrodynamics, 2022, 34(2): 286 − 298. doi: 10.1007/s42241-022-0023-6
[32]	LIANG L X, YU X P, BOMBARDELLI F. A general mixture model for sediment laden flows [J]. Advances in Water Resources, 2017, 107: 108 − 125. doi: 10.1016/j.advwatres.2017.06.012
[33]	GARSIDE J, AL-DIBOUNI M R. Velocity-voidage relationships for fluidization and sedimentation in solid-liquid systems [J]. Industrial & Engineering Chemistry Process Design and Development, 1977, 16(2): 206 − 214.
[34]	KHAN A R, RICHARDSON J F. Fluid-particle interactions and flow characteristics of fluidized beds and settling suspensions of spherical particles [J]. Chemical Engineering Communications, 1989, 78(1): 111 − 130. doi: 10.1080/00986448908940189
[35]	ANDERSEN K H, FARACI C. The wave plus current flow over vortex ripples at an arbitrary angle [J]. Coastal Engineering, 2003, 47(4): 431 − 441. doi: 10.1016/S0378-3839(02)00158-8
[36]	SLEATH J F A. Sea bed mechanics [M]. Wiley, United States, New Jersey, 1984: 335.
[37]	LEWIS A W, HITCHING E, PERRIER G, et al. Flow over ripples: Models and experiments [C]// Proceedings of the 2nd International Conference on Coastal Dynamics. Gdynia, Poland: ASCE, 1995: 686 − 697.
[38]	NAKATO T, LOCHER F A, GLOVER J R, et al. Wave entrainment of sediment from rippled beds [J]. Journal of the Waterway, Port, Coastal and Ocean Division, 1977, 103(1): 83 − 99. doi: 10.1061/JWPCDX.0000020
[39]	RAMADAN K A H, RIBBERINK J S. Time-averaged sediment transport phenomena in combined wave-current flows [R]. The Netherlands: Delft Hydraulics, 1994: 21 − 27.
[40]	MAGAR V, VAN DER WERF J J, EIDSVIK K J, et al. Comparison between 2DV sediment transport models and measurements of suspended sediment dynamics over full-scale ripples in oscillatory flows [M]// VAN RIJN L C, SOULSBY R L, HOEKSTRA P, et al. Sand Transport and Morphology of Offshore Sand Mining Pits. Amsterdam, The Netherlands: Aqua Publications, 2005: 1 − 13.
[41]	VAN DER WERF J J, DOUCETTE J S, O'DONOGHUE T, et al. Detailed measurements of velocities and suspended sand concentrations over full-scale ripples in regular oscillatory flow [J]. Journal of Geophysical Research: Earth Surface, 2007, 112(2): F02012.
[42]	HUNT J C R, WRAY A A, MOIN P. Eddies, streams, and convergence zones in turbulent flows [C]// Proceedings of the Summer Program. Stanford: Center for Turbulence Research, 1988: 193 − 208.
[43]	MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications [J]. AIAA Journal, 1994, 32(8): 1598 − 1605. doi: 10.2514/3.12149

施引文献(11)

期刊类型引用(9)

1.	张元海，马云亮，刘泽翔. 偏载作用下薄壁箱梁空间整体效应的综合分析. 土木工程学报. 2024(04): 48-58 . 百度学术
2.	王珊珊，陈浩，程浩，王俊. 轨道交通“双U+箱形”截面桥梁剪力滞效应简化计算方法. 南京工业大学学报(自然科学版). 2023(03): 300-307+322 . 百度学术
3.	雒家琪，董毓利，赵明岩. 集中荷载和均布荷载作用下悬臂箱梁剪力滞效应试验. 华侨大学学报(自然科学版). 2022(01): 44-50 . 百度学术
4.	陈建民，骆维斌，冀伟. 变截面箱梁桥悬臂施工过程剪力滞效应. 科学技术与工程. 2022(31): 13950-13957 . 百度学术
5.	袁晗，王小军，张宏剑，牟宇，王檑，王辰. 重复使用火箭着陆缓冲的机构冲击动力学分析及实验验证. 北京大学学报(自然科学版). 2022(06): 977-988 . 百度学术
6.	刘应龙，蔺鹏臻，何志刚，马俊军，孙理想. 箱梁剪力滞效应分析的梁条方法及模型. 应用基础与工程科学学报. 2021(03): 718-728 . 百度学术
7.	朱绪江，郭健，方明山，谭昱. 斜拉桥变宽度主梁的剪力滞效应分析. 工程力学. 2021(S1): 93-99 . 本站查看
8.	卫星，古兴宇，戴李俊，肖林. 轨道交通W型槽梁在顶推施工中时变剪力滞效应. 中国测试. 2021(06): 91-94 . 百度学术
9.	潘旦光，韦杉杉，LU Pan，鲁文艳. 变高度简支箱梁剪力滞半解析解. 力学季刊. 2019(04): 796-806 . 百度学术