在被保护建筑周围布置波屏障(如空沟、连续墙和排桩等)以阻止弹性波传播是一种有效阻隔地震动或环境振动的方法，具有施工方便、造价低廉和隔震减振效果好等优点，目前已在工程中广泛应用^[1-3]。

近年来，研究者们引入固体物理学中声子晶体型周期性结构的概念进行隔震基础和波屏障设计^[4-9]，利用周期结构的滤波特性来实现振动抑制，即某些频段的弹性波不能透过周期结构继续传播，这一特定频段称为带隙或衰减域^[10]。2013年，HUANG和SHI^[6]率先研究了弹性波在周期性排桩屏障中的传播特点，并用衰减域的形成机理解释了多排桩对弹性波的散射特性。但是基于Bragg散射机理设计的周期波屏障的第一带隙中心频率对应的波长与周期性单元尺寸相当，一般需要较大的单元尺寸才能实现低频振动抑制，目前主要用于缓解地铁运行所致环境振动(主频段为40 Hz~80 Hz)^[11]。而地震Rayleigh波具有频率低(主频段为0.1 Hz~10 Hz)、波长大、携带能量大等特点，是中远场地震波的主要成分。对于大型桥梁、浅埋地下结构和核电屏蔽厂房等抗震设防要求高的结构，地震Rayleigh波的影响不容忽视^[12]。因此，亟需发展一种新型的隔震技术用于低频表面地震动衰减。

2004年，LI和CHAN^[13]通过类比电磁波超材料的“双负”特性，发现了具有负体积模量和负等效质量的声学复合超材料，并首次将这类复合材料命名为声学超材料。与声子晶体带隙形成机理不同，声学超材料是由亚波长尺度的基本单元组成，通过子结构的局域共振与波长较长的弹性行波相互作用，在系统共振频率附近表现出负参数特性。局域共振概念的提出突破了Bragg散射型周期结构在低频应用的困境，实现了结构的小尺寸控制大波长，极大地扩宽了超材料结构在工程领域的可设计性和应用范围^[14-16]。目前，已有研究者将局域共振超材料结构的概念引入土木工程领域，开展超材料基础和波屏障的带隙特性及其隔震性能研究^[17-22]。

2016年，PALERMO等^[18]提出将单质点弹簧振子模型布置在弹性半空间自由表面形成表面超屏障，并基于有效介质方法和弹性波理论推导了Rayleigh波在表面超屏障中传播的频散方程。研究结果表明：米尺寸表面超屏障的竖向共振模态与Rayleigh波竖向位移分量强烈耦合产生表面波带隙，可以有效控制波长在10 m~100 m的地震表面波。随后，ZEIGHAMI等^[19]类比表面超屏障的概念，从弹性波动方程出发，推导了单质量弹簧振子和基质土组成的局域共振超屏障的理论频散方程，并利用有限元方法对超屏障的屏蔽效果进行频域分析。PALERMO等^[18]和ZEIGHAMI等^[19]的研究工作为超材料结构衰减低频地震表面波提供了理论指导，进一步推动了表面超屏障的后续研究，如文献[20]研究了饱和土中垂直极化Rayleigh波与表面超屏障的耦合效果，并指出流固耦合作用导致杂化Rayleigh波以慢压缩波的形式泄漏到基体中，形成更大的衰减域；文献[21]基于成层半空间中Rayleigh波的频散特性，推导了成层半空间中Rayleigh波与表面超屏障耦合的频散关系，并揭示了各阶表面波模态与表面超屏障的耦合规律。综上所述，虽然目前国内外研究者基于局域共振特性开展了大量表面超屏障衰减地震表面波研究，但是仍然存在屏障占地面积较大、与土壤表面的有效接触、衰减效果不佳等尚未解决的问题，在实际工程中较难实现。

针对Rayleigh波沿深度方向上呈指数形式衰减的特点，以及文献[21]指出的土壤分层导致表面超屏障衰减弱化的现象，本文提出沿深度方向周期性布置超材料单元形成埋地超屏障，以期实现更好的衰减效果。首先，基于均匀化近似方法和弹性动力学理论，推导了全共振半空间和有限埋深超屏障的理论频散方程；其次，采用有限元方法验证理论频散关系的准确性，探究不同埋深超屏障表面波带隙的变化规律；最后，通过频域分析和瞬态分析对埋地超屏障和Bragg散射型周期波屏障的衰减性能进行对比研究，凸显了埋地超屏障具有衰减低频地震表面波的优势，有望作为一种新型隔震技术应用于工程实践。

1   埋地超屏障理论模型及频散方程

1.1   问题描述

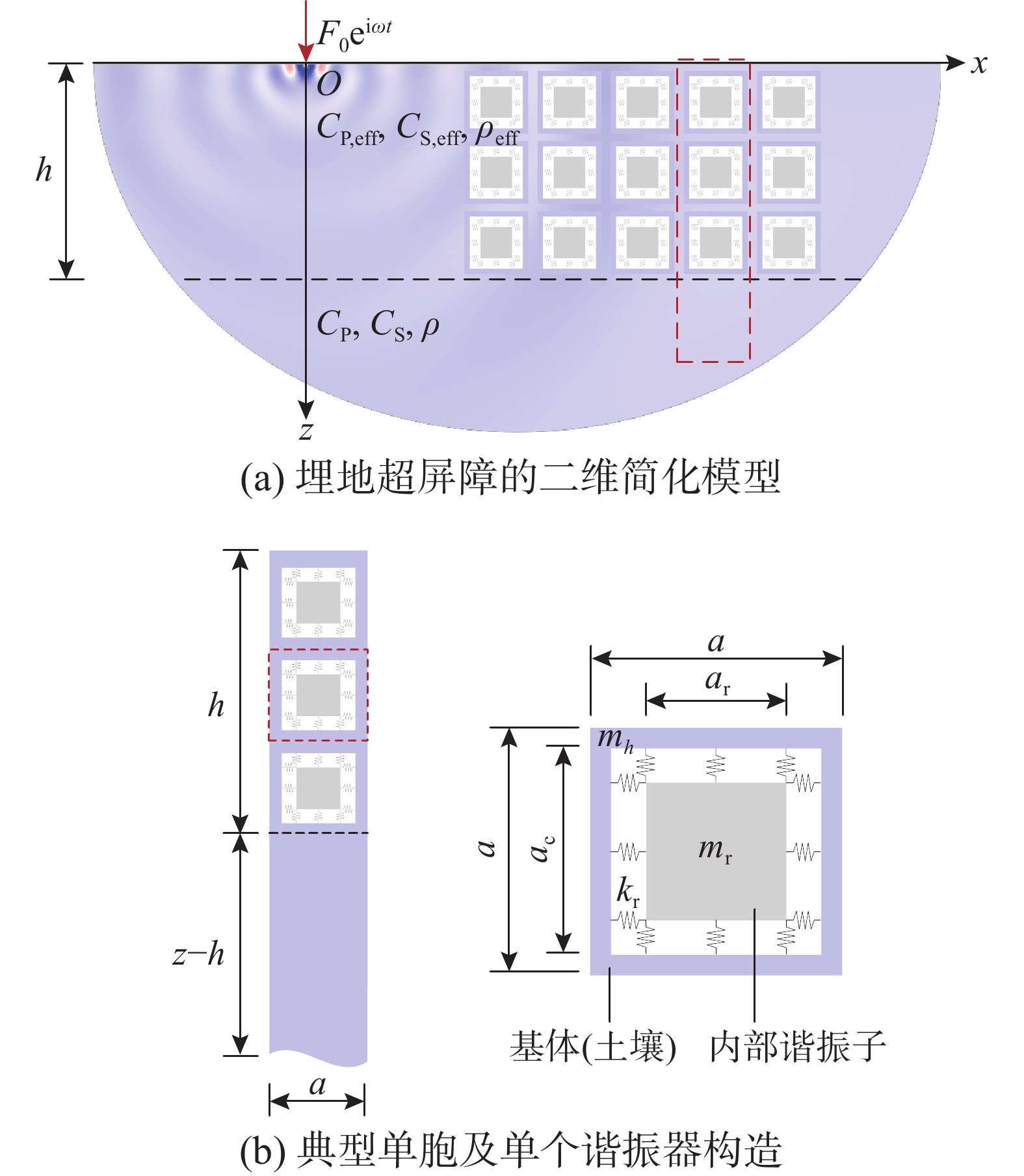
如图1(a)所示，竖向谐波激励在弹性半无限空间近自由表面处产生沿x轴方向传播的表面波，埋地超屏障由谐振器单元(图1(b))沿y轴和z轴按正方排布而成。为简化分析，假定埋地超屏障沿y轴方向无限布置，沿深度方向的布置深度为h，土壤为均匀、各向同性的线弹性材料，且不考虑阻尼耗能。米尺寸的谐振器单元由质量为m_r的内部谐振子和外部土壤通过刚度为k_r水平和竖向弹簧相连，具体的几何尺寸及其内部构造如图1(b)所示。由于谐振器单元尺寸远小于目标频率范围(0.1 Hz~10 Hz)内的表面波波长，根据有效介质方法^[18-21]和局域共振超材料的“有效”属性^[13]，由谐振器单元组成的共振层可以近似为具有频率依赖性的“有效”均质材料，其力学属性可用有效压缩波速C_P,eff、有效剪切波速C_S,eff和有效密度ρ_eff来描述。而深度在z−h范围的土壤参数仍采用压缩波速C_P、剪切波速C_S和密度ρ来描述。

图  1  埋地超屏障的二维简化模型及其典型单胞

Figure  1.  2D simplified model of buried metabarrier and its typical unit cell

下载: 全尺寸图片 幻灯片

1.2   共振层的有效属性计算

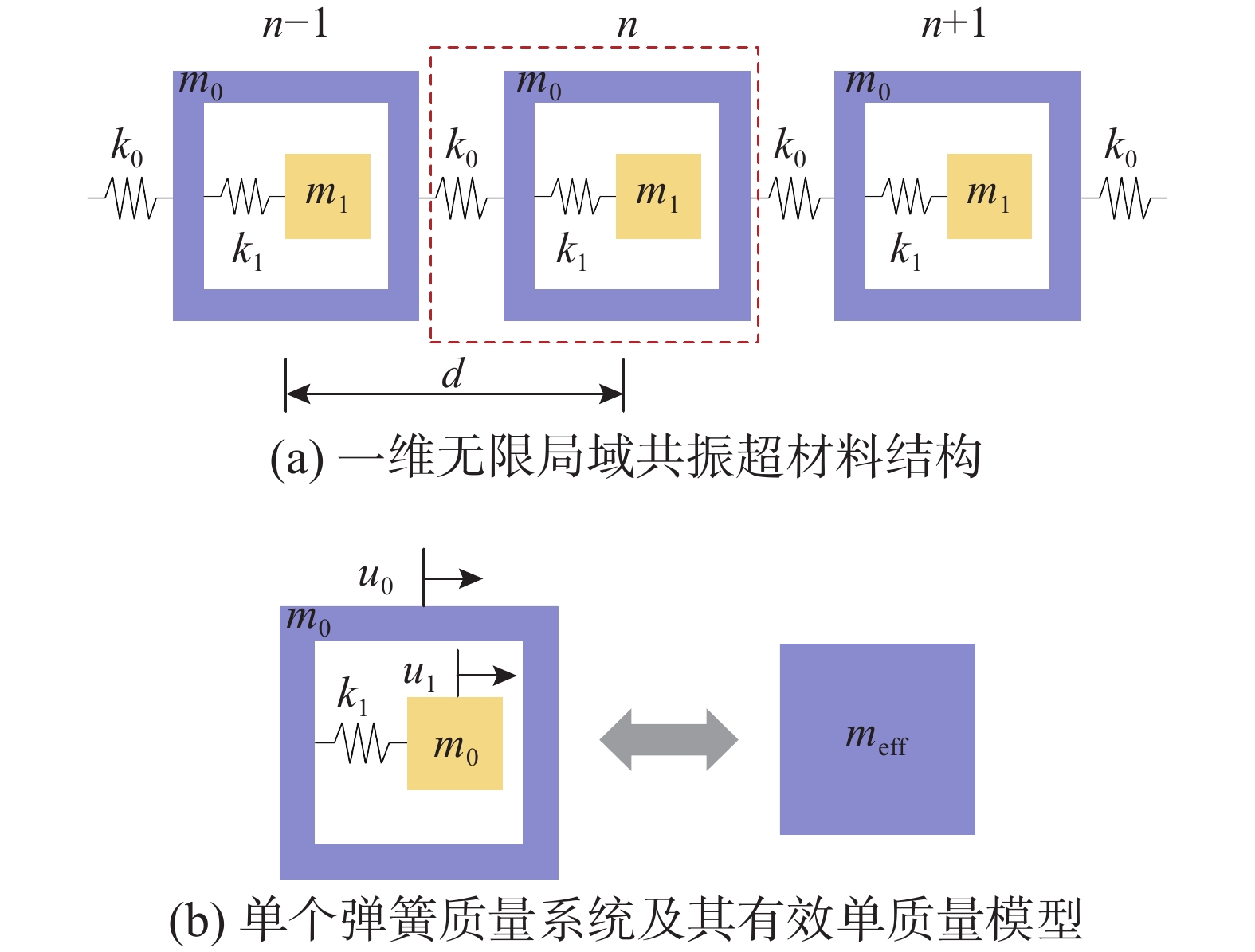
为了建立埋地超屏障的频散方程，本节首先基于局域共振超材料的“有效”属性，近似计算共振层的有效力学参数。图2(a)表示一维无限局域共振超材料结构模型，由外部腔体${m_0}$和内部弹簧振子k₁-m₁组成的超材料单元由弹簧${k_0}$相连，并以周期常数d沿水平方向无限排布而成。

取第n个超材料结构单元如图2(b)所示，典型单元的运动微分方程为：

式中：${u_0}$为外部腔体的位移；${u_1}$为内部振子的位移。

假定运动方程的谐波解形式为：

式中，${\overline u_1}$和${\overline u_0}$分别为内部谐振子和外部腔体的位移幅值。由式(2)可知，内部谐振子和外部腔体位移幅值的关系可表示为：

有效质量m_eff可定义为与单个弹簧质量系统具有相同动量的单质量模型，即：

将式(3)代入式(4)可以得到：

式中：${\omega _1} = \sqrt {{k_1}/{m_1}}$为内部谐振子的共振频率；ω为圆频率。

因此，图1(b)中单个谐振器的有效质量密度可表示为：

式中：V为单个谐振器的体积，对于二维平面应变模型，假定平面外厚度t=1 m，则V=a²；ρ₀=(m_h+m_r)/V为静态密度；η=m_r/(Vρ₀)为单位体积内部谐振子质量与静态密度ρ₀的比值。

图  2  含单个谐振器的局域共振超材料集总参数模型

Figure  2.  Lumped parameter model of locally resonant metamaterials with a single resonator

下载: 全尺寸图片 幻灯片

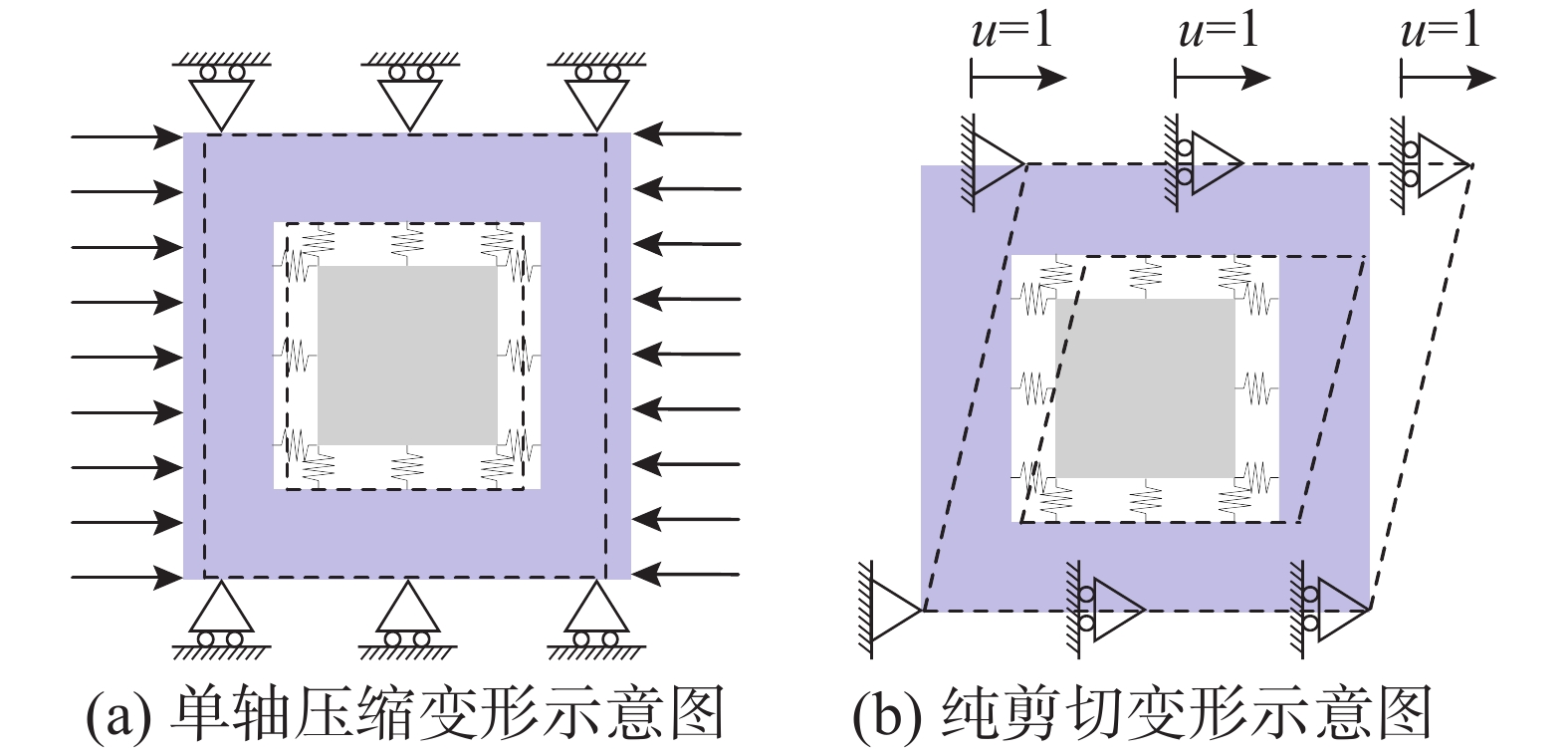
基于有效介质方法^[18-21]，假定在低频范围内谐振器单元是各向同性的，共振层可以近似为具有频率依赖性的“有效”均质材料，其有效弹性参数(有效压缩模量M_eff和有效剪切模量μ_eff)通过谐振器单元在静力下的压缩模量和剪切模量近似估计。因此，在单轴压缩和纯剪切变形状态下，谐振器单元的两个弹性参数可表示为^[19]：

其中：

式中：${\overline \sigma _{xx}}$和${\overline \varepsilon _{xx}}$分别为单轴压缩状态下谐振器单元基体材料的平均压应力和压应变分量；${\overline \tau _{x{\textit{z}}}}$和${\overline \gamma _{x{\textit{z}}}}$分别为纯剪切变形状态下外部基体顶部的平均剪应力和剪应变分量。

共振层的有效压缩波速C_P,eff和有效剪切波速C_S,eff可由具有频率依赖性的有效密度ρ_eff(ω)表示为：

1.3   全共振半空间中的Rayleigh波方程

首先考虑一种极限情况，当超屏障埋深$h \to \infty$时，半空间完全由谐振器单元组成，简称全共振半空间。由1.2节可知，全共振半空间的力学参数可用有效压缩波速、有效剪切波速和有效密度来表示。全共振半空间中Rayleigh波的波函数可由标量势$\phi$和矢量势${{\boldsymbol{\psi}} _{\rm{y}}}$表示为：

式中：A₁和B₁分别为振幅；i为虚数单位；k为波数；c为波速；a和b可表示为：

弹性波场的位移和应力分量为：

将自由表面边界条件：

和Rayleigh波函数代入式(15)~式(17)可得：

要使式(19)有非奇异解，其系数行列式应为0，即：

将式(14)代入式(20)并化简得：

式(21)即为全共振半空间中Rayleigh波的频散方程。可以看出，全共振半空间的Rayleigh波方程与均质半空间的Rayleigh方程形式相同，只是其力学参数用超材料单元的“有效”参数代替。

1.4   有限埋深超屏障中Rayleigh波的频散方程

其次考虑一种更为实际的情况，即超屏障的埋置深度h是有限的。由1.1节和1.2节分析可知，有限深度共振层和无限深度土体组成的半空间可视为一种特殊的成层半空间。因此，半空间有限埋深超屏障中Rayleigh波的频散方程可参考成层半空间中Rayleigh波特征方程的推导过程^[23]，即：

受篇幅所限，式(22)的求解过程详见文献[23]的式(23)~式(27)。重新组织特征方程可得：

式中，T_i为相邻介质状态量的传递函数。

式(23)用递推形式表达为：

式中，Y₁(1, 2)为矩阵Y₁的第一行第二列元素。

注意到矩阵Y_n+1为反对称矩阵，根据反对称矩阵的性质，将式(24)用矩阵元素的运算表示为：

式中：W_m和W_m+1分别为由矩阵Y_m和Y_m+1中的六个非零元素组成的行向量；${\boldsymbol{T}}_m^*$为T_m的δ矩阵。

根据δ矩阵的性质及${{\boldsymbol{T}}_m} = {{\boldsymbol{H}}_m}{{\boldsymbol{E}}_m}{\boldsymbol{H}}_m^{ - 1}$，式(26)可进一步化简为：

式中：${\boldsymbol{H}}_m^*$、${\boldsymbol{E}}_m^*$和${\left( {{\boldsymbol{H}}_m^{ - 1}} \right)^*}$分别为${{\boldsymbol{H}}_m}$、${{\boldsymbol{E}}_m}$和${\boldsymbol{H}}_m^{ - 1}$的δ矩阵，各矩阵的元素详见文献[23]附录；${{\boldsymbol{W}}_m}$的起始向量为：

式中，γ = 2(C_S/c)²。相应的频散方程(式(25))可进一步表示为：

式中，W₁(1, 1)为矩阵W₁的第一行第一列元素。此外，需要指出的是，虽然本节讨论的是均一土体中有限埋深超屏障的频散特性，但是利用传递矩阵方法^[23]，均质半空间有限埋深超屏障中Rayleigh的频散关系可以推广到成层半空间中。特别地，当式(28)中n=0时，式(29)即为有限埋深超屏障中Rayleigh波的频散方程。

2   埋地超屏障频散特性分析

采用土壤和钢材组构造超材料单元，其中土壤的弹性模量、密度和泊松比分别为46 MPa、1800 kg/m³、0.25，钢材的力学参数相应为209 GPa、7890 kg/m³、0.275。根据给定的土壤参数，可求得在1 Hz~10 Hz内，Rayleigh波的波长λ_R范围为9 m~93 m。根据有效介质方法的适用条件(${\lambda _{\rm{R}}} \gg a$)，超屏障的单元常数取a=1 m，内部谐振子的边长a_r=0.4 m，内部谐振子与基体土通过刚度为k_r的12根弹簧相连。假设内部谐振子的自振频率f_r=4 Hz，求得谐振器的基本力学参数如表1所示。

表  1  谐振器力学参数

Table  1.  Mechanical parameters of a resonator

设计参数	取值
外部基体质量mh/kg	1152
内部谐振子质量mr/kg	1262.4
弹簧刚度kr/(N·m)	1.329×105
谐振器共振频率fr/Hz	4

下载: 导出CSV 

| 显示表格

2.1   局域共振单元的有效属性计算

根据1.2节分析可知，为了得到共振层的有效波速，应首先通过静力方法求得谐振器单元的压缩模量和剪切模量。本文采用有限元软件COMSOL建立单个谐振器的二维平面应变模型，如图3所示。基体土和内部谐振子采用二次拉格朗日实体单元模拟，水平和竖向弹簧采用桁架单元模拟。由于实体单元和桁架单元的节点自由度不一致，因此需要统一共节点处的位移来实现基体土与谐振子的弹性连接。

图  3  单个谐振器的弹性参数计算模型示意图

Figure  3.  Schematic of elastic parameter calculation model of a single resonator

下载: 全尺寸图片 幻灯片

通过在谐振器单元的侧向施加单位压力荷载，并约束其上下边界的竖向位移，来模拟谐振器单元的单轴压缩状态；通过在谐振器单元的上边界施加单位位移，并约束其下边界的水平位移，来模拟谐振器单元的水平纯剪切状态。图4给出了单轴压缩和纯剪切变形时谐振器单元的应力和应变分量云图。根据式(7)求得谐振器单元的压缩模量为M_eff=53.64 MPa，剪切模量为μ_eff=2.43 MPa。

图  4  单轴应力状态下谐振器单元的应力和应变分量

Figure  4.  Stress and strain components of a single resonator under uniaxial stress state

下载: 全尺寸图片 幻灯片

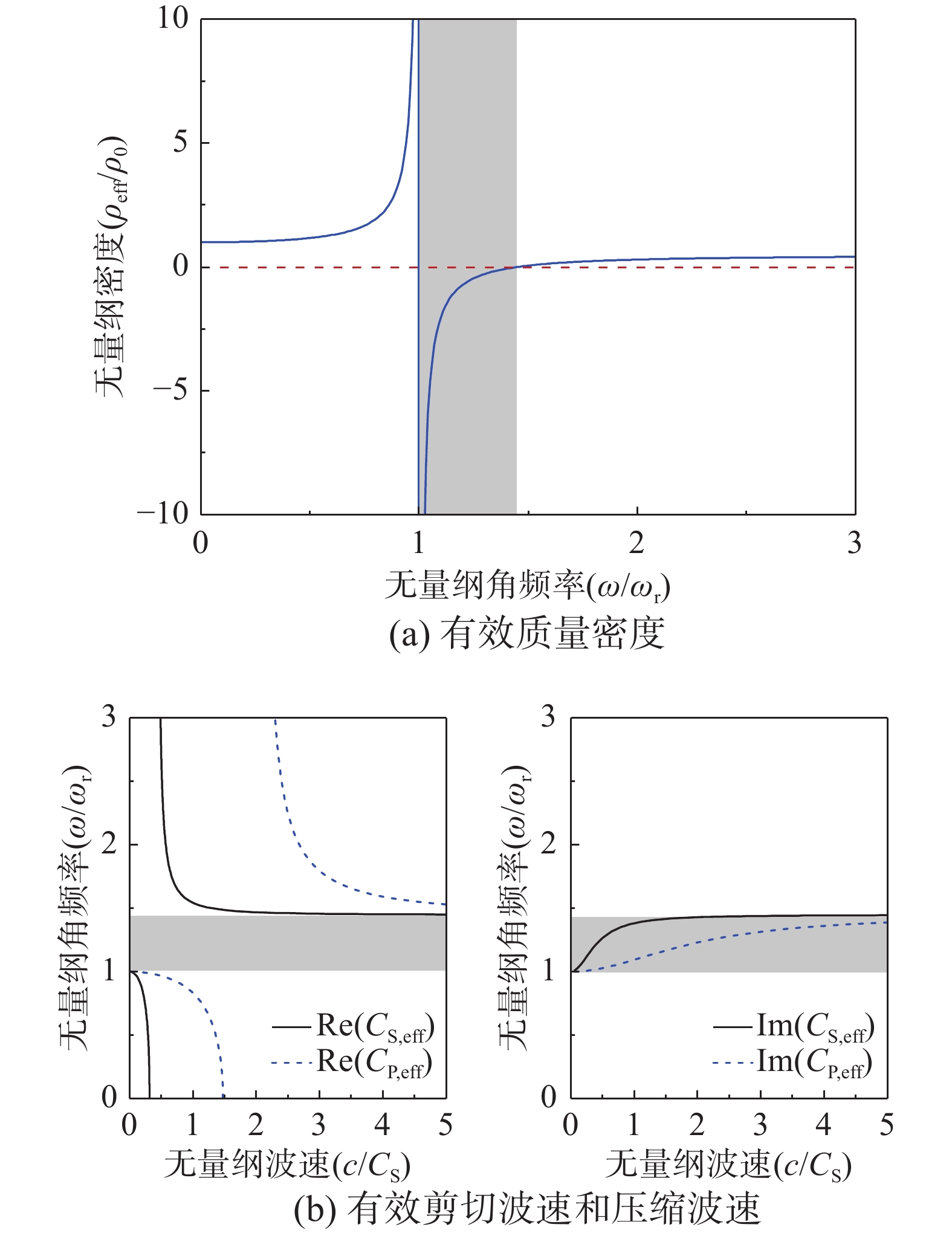
针对本文设计的谐振器单元，当单元常数a=1 m，谐振器的体积V=1 m³。由式(6)可得其静态质量密度ρ₀=2414.4 kg/m³，外部基体的质量m_h=1152 kg，单位体积内部谐振子质量与静态质量的比值η= m_r/(Vρ₀)=0.523。图5(a)给出了谐振器单元与频率相关的有效密度曲线，其中纵轴表示无量纲密度(ρ_eff/ρ₀)，横轴表示无量纲角频率(ω/ω_r)。由图5(a)可知，有效密度曲线可根据无量纲角频率的取值范围划分为三段：当$\omega /{\omega _{\rm{r}}} \in (0,1)$时，有效密度值均大于零，且随着频率的增加逐渐变大；当$\omega /{\omega _{\rm{r}}} \in (1,1/\sqrt {1 - \eta } )$时，由于内部谐振子与基体的反向运动，有效密度曲线变为负值(图5(a)中阴影区域)，且随着频率的增加逐渐变大；当$\omega /{\omega _{\rm{r}}} \in (1/\sqrt {1 - \eta } ,\infty )$时，有效密度值从负值变为正值，并随着频率的增加缓慢增大。值得注意的是：当$\omega \to 0$时，${\rho _{{\rm{eff}}}} \to {\rho _0}$，即在极低频段内，有效密度趋向于静态密度；当$\omega \to \infty$时，${\rho _{{\rm{eff}}}} \to \left( {1 - \eta } \right){\rho _0}$，即在高频段内部谐振子对谐振器单元的有效质量几乎没有贡献。此外，负密度区间的长度取决于η的大小，单位体积内部谐振子质量与静态质量的比值越大，负密度区间越长。

图5(b)表示共振层有效压缩波速和剪切波速与角频率的关系曲线，其中纵轴表示无量纲角频率，横轴表示无量纲波速(c/C_S)。可以发现，在有效密度为负值的区域，有效体波波速的实部为零，仅有呈指数衰减的波的虚部，且有效波速虚部表现出典型局域共振周期结构衰减因子的非对称特性。

图  5  谐振器单元的有效属性

Figure  5.  Effective properties of the resonator

下载: 全尺寸图片 幻灯片

2.2   全共振半空间中Rayleigh波的频散特性及有限元验证

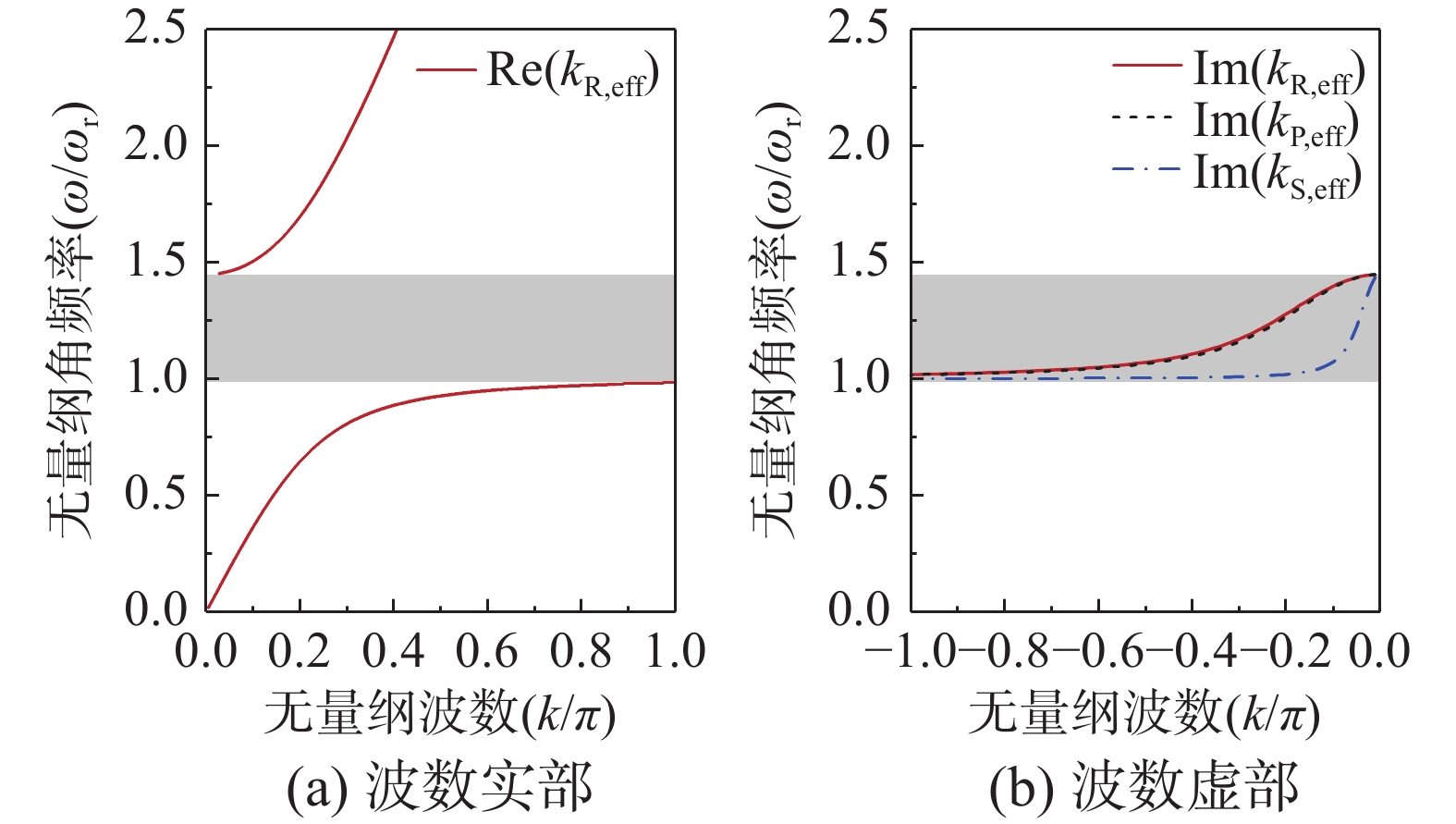
求解隐函数方程式(21)可得全共振半空间表面波关于波数和角频率的关系，如图6所示。可以看出，在阴影区域不存在实波数与角频率的对应关系，即全共振半空间表面波带隙宽度为谐振器单元的负密度区域。根据弹性半空间自由表面附近Rayleigh波的形成原因，可对全共振半空间表面波带隙形成机理进行解释：Rayleigh波是由具有相同传播速度的平面压缩波和平面剪切波叠加形成的，由图5(b)可知，有效压缩波和剪切波在谐振器单元的负密度区间被阻隔，因此有效Rayleigh波在全共振半空间的负密度区间也无法传播。

另外，图6给出了全共振半空间中Rayleigh波和体波关于虚波数Im(k)和无量纲角频率的对应关系。不难发现，全共振半空间中有效Rayleigh波的衰减因子Im(k_R,eff)与有效剪切波的衰减因子Im(k_S,eff)相近，且大于有效压缩波的衰减因子Im(k_P,eff)，这是由于波数的虚部与波速的虚部成反比，即Im(k)=ω/Im(c)；有效Rayleigh波衰减因子与有效压缩波衰减因子的比值Im(k_R,eff)/Im(k_P,eff)可等效为有效压缩波波速虚部与有效Rayleigh波波速虚部的比值Im(C_P,eff)/Im(C_R,eff)。对比有效剪切波和Rayleigh波的相应参数也可以得出相似结论。

图  6  全共振半空间中Rayleigh波的频散关系曲线

Figure  6.  Dispersion curves of Rayleigh waves propagating through fully resonant half space

下载: 全尺寸图片 幻灯片

为了验证全共振半空间Rayleigh波理论波频散关系的准确性，采用COMSOL建立全共振半空间单胞的二维平面应变有限元模型。如图7(a)所示，单胞的宽度为a，高度为3λ_r，其中λ_r=C_R/f_r=23 m表示内部谐振子共振频率处的Rayleigh波长。因此，该单胞模型的高度足以模拟共振频率附近的半空间域。在单胞底部施加固定边界，避免发生刚体位移，同时沿周期方向施加Bloch边界条件。为了保证数值计算结果满足收敛性要求，采用二次拉格朗日单元对实体域进行离散，网格的最大和最小尺寸分别为d_max=a/5和d_min=a/10。通过在不可约布里渊区边界扫描波数k，即可求得全共振半空间的数值频散关系。

需要指出的是，采用有限元方法得到的数值频散关系包含体波和面波模态，为了从所有解中筛选出面波模态对应的解，本文参考PU等^[24]提出的表面波模态识别方法。图7(a)给出了第一不可约布里渊区内实波数对应的所有特征频率，其中数值表面模态用红色圆点表示，其余数值解用原点表示，实线表示全共振半空间中Rayleigh波的理论频散关系曲线。可以看出，数值解与解析解吻合良好，说明在低频范围内有效介质方法能准确描述埋地超屏障的动力特性。

图7(b)给出了数值频散关系中某些特征点处的竖向位移场分布，这些特征点在图7(a)中用星号标出，其中A点、B点、C点的无量纲波数均为0.35，无量纲角频率分别为0.86、2.2和1.41。为了方便观察特征点处基体和内部谐振子的运动情况，沿波传播方向按相位e^ikx变化来复制单胞的特征模态，水平传播长度为15a。图7(b)中特征点A对应表面波频散曲线的下分支，可以看出外部基体与内部谐振子保持同相运动，而在特征点B处，外部基体与内部谐振子运动方向相反(相位差为π)，这也进一步说明了表面波带隙的形成源于内部谐振子的反相运动。当无量纲频率为1.41时，频散关系数值解中出现一条水平分支，如图7(b)中水平点所示。根据特征点C处位移场分布可知，水平分支处的特征模态对应于内部谐振子的扭转运动。

图  7  全共振半空间频散关系的数值解及其特征模态

Figure  7.  Numerical solutions and characteristic modes of dispersion relation in fully resonant half space

下载: 全尺寸图片 幻灯片

2.3   有限埋深超屏障中Rayleigh波的频散特性及有限元验证

根据1.4节有限埋深超屏障中频散方程的推导过程，编制相应的计算程序，求得共振层厚度h分别为0.05λ_r、0.2λ_r和0.5λ_r的理论频散关系曲线，并引入声锥判别法来分析有限埋深超屏障的表面波带隙。根据声锥判别法可知，声锥的声线对应于该传播方向基体中的最小相速度，因此纯表面波模态仅存在声线以下。从图8(a)~图8(c)可以看出，随着埋深增加，超屏障中出现多种杂化表面波模态，如图8(a)~图8(c)中实线表示。表面波频散曲线可分为上下两部分，为方便描述，两部分频散曲线的第一杂化表面波模态称为基本模态。杂化表面波与谐振子的耦合导致在共振频率附近出现表面波带隙，带隙的起始频率为谐振子的共振频率，截止频率为声线与表面波频散曲线基本模态的交点。

图  8  不同埋深超屏障的理论频散关系曲线

Figure  8.  Theoretical dispersion curves of metabarriers with different buried depths

下载: 全尺寸图片 幻灯片

图8(b)和图8(c)中虚线表示全共振半空间表面波带隙的截止频率，可以发现，随着共振层厚度的增加，表面波带隙的宽度逐渐增大，当超屏障埋置深度增加至0.5λ_r时，有限埋深超屏障的表面波带隙宽度大于全共振半空间的表面波带隙。进一步地，图8(d)给出了超屏障埋深从0.05λ_r增加到λ_r时表面波带隙宽度的变化情况。不难看出，超屏障埋置深度达到0.5λ_r时，继续增加埋置深度，带隙宽度保持不变。这一现象可以根据有限埋深超屏障表面波带隙形成机理来解释：首先，随着超屏障埋深增加，在谐振器的负密度区间，共振层内的体波模态被显著抑制，由体波模态叠加而产生的表面波模态也被抑制；其次，在全共振半空间表面波带隙之上的频率范围(虚线到表面波带隙的截止频率范围)内，表面波模态的表观相速度值大于基体剪切波速，因此，该频段内表面波以漏波模态的形式存在，从而导致表面波带隙扩宽。

另外，当超屏障埋深h=0.05λ_r≈1 m时，相当于仅在半空间近地表埋置了一层谐振器单元。图8(a)给出了分别按照均质半空间表面超屏障(文献[18])和埋地超屏障(式(27))计算的频散关系对比。可以看出，埋深较浅的埋地超屏障与表面超屏障的频散关系基本相同，因此薄共振层可近似等效为半空间自由表面的应力边界条件。

为验证有限埋深超屏障理论频散关系的有效性，以埋深h=λ_r的超屏障为例，建立有限埋深超屏障的单胞有限元模型，如图9(a)所示。采用与全共振半空间数值频散分析相同的边界条件、离散方法和网格尺寸，求得埋深为λ_r的超屏障数值频散关系。其中圆点表示采用能量分布参数法筛选出来的表面波模态，实线表示按照式(27)求得的基本表面波模态的频散关系。可以看出，数值解与解析解吻合良好，进一步说明了本文理论分析的可靠性。

图9(b)给出了数值频散关系中特征点对应的竖向位移场分布，其中A、B、C点的无量纲波数均为0.35，无量纲角频率分别为0.86、2.2和1.41，D点位于声锥内部，其无量纲波数为0.1，无量纲角频率为1.52。与全共振半空间频散曲线中特征点处的位移场分布类似，模态A、模态B和模态C分别表示外部基体和内部谐振子的同相、反相运动以及谐振子的扭转模态。特别地，从D点的位移场分布可以看出，在超屏障范围内基体与内部谐振子发生反相运动，此外一部分表面波能量泄漏至弹性半空间域，导致表面波带隙拓宽。

图  9  有限埋深超屏障频散关系的数值解及其特征模态

Figure  9.  Numerical solutions and characteristic modes of dispersion relation of finite buried metabarrier

下载: 全尺寸图片 幻灯片

3   有限埋地超屏障衰减性能研究

3.1   传输分析模型

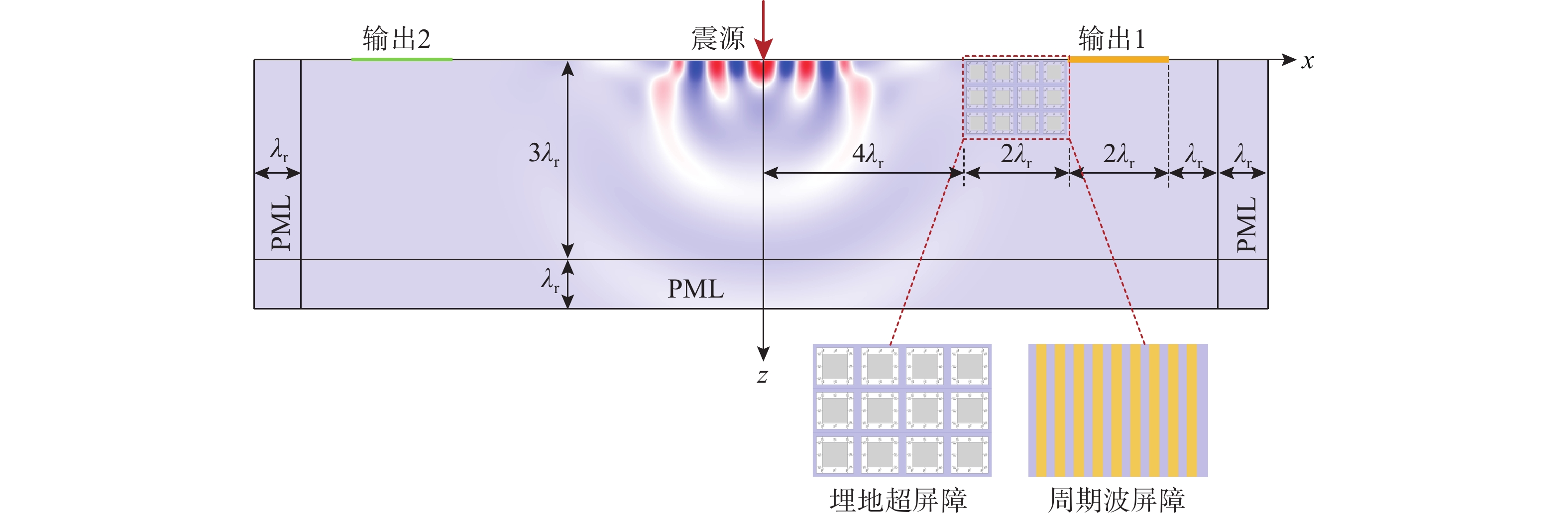
为说明埋地超屏障的低频衰减源于内部谐振子在共振频率附近的反相运动，本节首先将谐振子单独作为散射体形成周期波屏障，散射体的宽度为a_r，埋深为0.5λ_r，并通过特征值分析和频域分析研究周期波屏障的频散特性和衰减特性。图10给出有限波屏障和参考自由场的传输谱分析模型，超屏障的几何尺寸、震源距和输出端位置等信息等均示于图中。数值模拟时，实体域的离散方法和网格尺寸均与2.2节和2.3节中单胞的特征频率分析保持一致，通过在震源位置施加单位谐波激励，对两种波屏障进行频域分析，并利用加速度衰减谱衡量其隔震效果^[21]；通过施加地震波荷载，对有无超屏障的传输模型的表面地震动响应进行瞬态分析。同时，为了避免弹性波在边界处发生反射，在频域分析时在计算域外侧施加完美匹配层，而在瞬态分析时采用COMSOL中内置的低反射边界条件来模拟弹性波在边界处的传播行为。

图  10  传输谱计算的几何模型示意图

Figure  10.  Schematic of geometrical model used for transmission spectrum calculation

下载: 全尺寸图片 幻灯片

3.2   频域分析

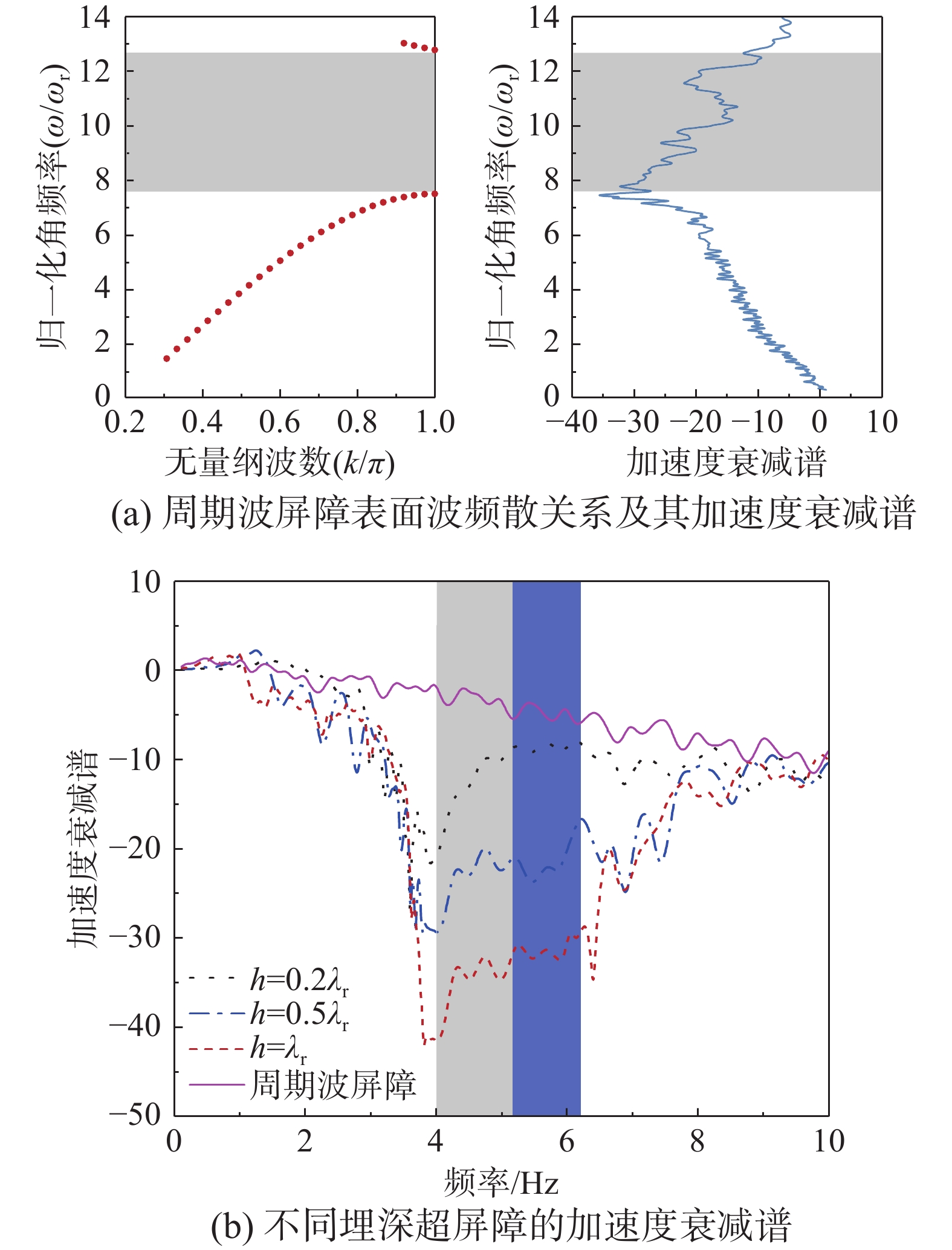
图11(a)给出了周期波屏障表面波频散关系曲线及其加速度衰减谱。可以看出，周期波屏障的无量纲表面波带隙范围(7.46~12.25)较宽，但起始频率远高于埋地超屏障，而且周期波屏障在低频段的加速度衰减并不明显。图11(b)对比了周期波屏障及埋置深度分别为0.2λ_r、0.5λ_r和λ_r的超屏障在0 Hz~10 Hz内的加速度衰减谱。从图11(b)中可以看出，不同埋深有限超屏障的加速度衰减谱在相应的表面波带隙范围内(图11(b)中阴影区域)出现明显衰减，并且衰减效果随着超屏障埋深的增加而增大。在频率带隙外部，不同埋深的超屏障和周期波屏障对表面波的阻隔效果大致相同。

图  11  埋地超屏障和周期波屏障的加速度衰减谱对比

Figure  11.  Comparison of ARSs between buried mrtabarrier and periodic wave barrier

下载: 全尺寸图片 幻灯片

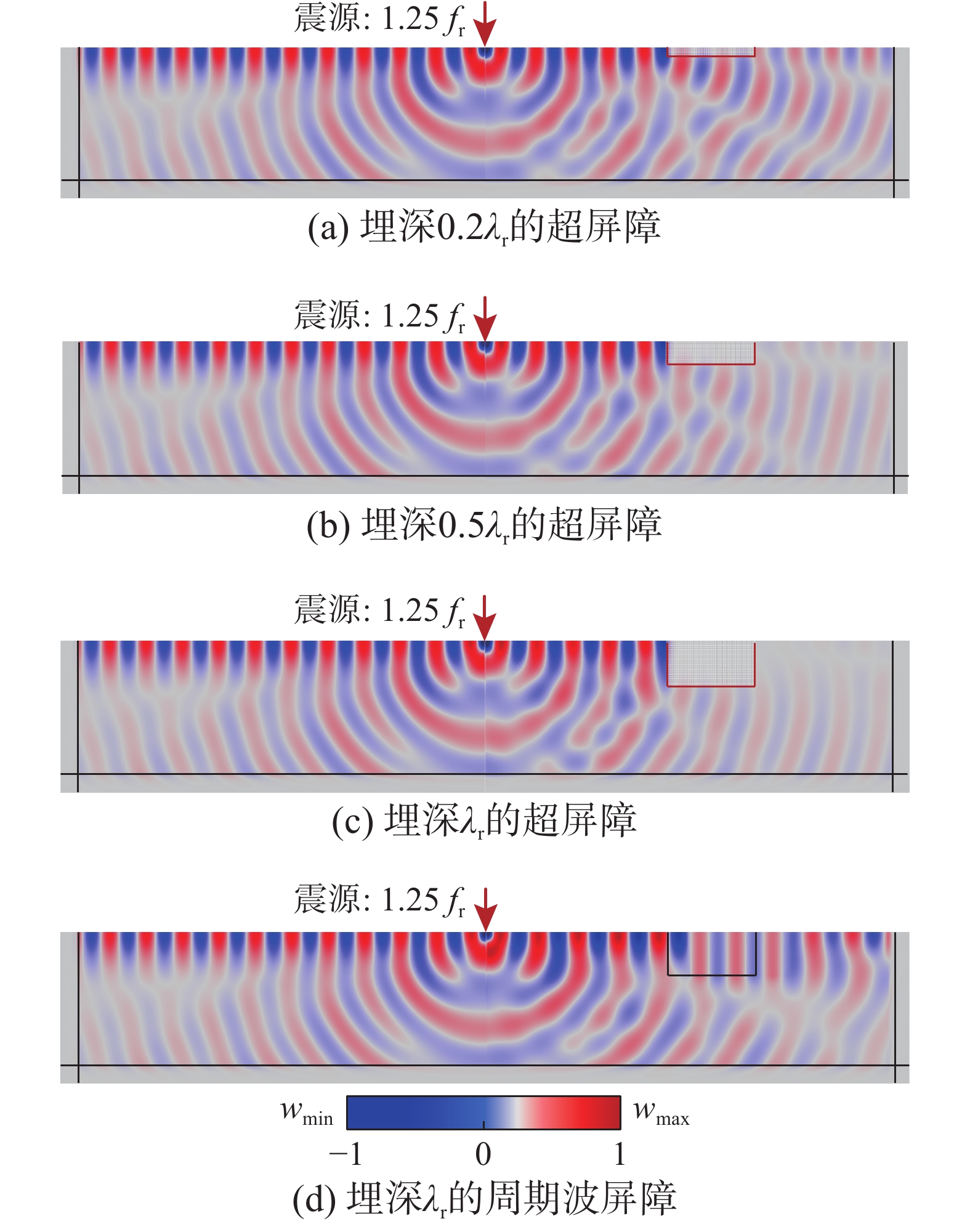
为了直观反映埋地超屏障的滤波特性，图12给出了无量纲频率为1.25f_r=5 Hz的谐波激励下，不同埋深超屏障和周期波屏障的竖向位移场分布云图。可以看出，埋地超屏障对带隙内部的谐波激励具有明显的衰减效果，并且输出端的竖向位移响应随着埋深的增加而逐渐减小，而周期波屏障输出端的位移响应与均质土输出端的位移响应相差不大，进一步说明了埋地超屏障衰减低频地震表面波的巨大潜力。

图  12  谐波激励下超屏障和周期波屏障的竖向位移响应

Figure  12.  The vertical displacement responses of metabarrier and periodic wave barrier under harmonic excitation

下载: 全尺寸图片 幻灯片

3.3   瞬态分析

对有无埋地超屏障的传输模型(图10)在真实地震动下的地表加速度响应进行瞬态分析。为了减少计算量，超屏障的埋深取0.5λ_r，即12个谐振器单元厚度。从PEER数据库选取Imperial Valley地震记录作为输入激励，峰值加速度为0.28 g，地震续时为53 s。

图13给出了Imperial Valley地震动作用下输出端1和输出端2的归一化加速度时程响应及其傅里叶谱。从图13中可以看出，在有埋地超屏障的情况下，输出端2的峰值加速度响应比自由表面(输出端1)加速度响应降低62%。同时，从加速度响应的傅里叶谱不难看出，在埋地超屏障的表面波带隙内(图13(b)中阴影部分)，动力响应幅值明显降低，这也进一步验证了埋地超屏障的低频衰减性能源于内部共振子的局域共振，而表面波带隙外高频段的幅值衰减可能是由于周期排布的内部共振子对表面波的散射作用。

图  13  输出端的归一化加速度响应及其傅里叶谱

Figure  13.  The normalized acceleration response of the output area and its Fourier spectrum

下载: 全尺寸图片 幻灯片

4   结论

针对Bragg散射型周期波屏障和表面超屏障带隙频段高、占地面积大、衰减效果不佳等不足，本文提出将局域共振超材料单元沿深度方向周期性布置形成埋地超屏障。基于有效介质方法，理论分析了全共振半空间和有限埋深超屏障中表面波带隙的形成机理，并利用有限元方法对理论结果进行验证；进一步通过频域和瞬态分析，研究了有限埋地超屏障和周期波屏障在谐波激励和地震动下的动力响应。得到主要结论如下：

(1)在低频范围内，当表面波长远大于超材料单元尺寸时，由复合材料组成的谐振器单元可近似为一种具有频率依赖性的各向同性的弹性均匀介质，其动力特性可由谐振器单元的有效密度和有效波速来表征。

(2)全共振半空间表面波的频率带隙范围与谐振器单元的负密度区间一致，即表面波带隙的形成源于内部谐振子与基体的反相运动。有限埋深超屏障表面波带隙宽度随埋深增加而增大，当超屏障埋深超过0.5λ_r时，在全共振半空间表面波带隙之上的声锥范围内，由于漏波模态的存在，表面波带隙拓宽。

(3)有限埋深超屏障既避免了Bragg散射机制中周期性单元尺寸过大的问题，又解决了表面超屏障占地面积大、与土壤表面接触不良的不足。且本文通过频域分析表明：有限埋地超屏障能有效抑制低频表面地震动；瞬态分析结果表明：在有埋地超屏障的情况下，输出端的峰值加速度响应降低了至少60%，凸显了埋地超屏障在衰减低频地震表面波方面的优异性能。