ANALYSIS AND OPTIMIZATION OF POST-EARTHQUAKE RESTORATION PRIORITY OF BRIDGE NETWORK UPON FRAGMENTATION
-
摘要:
为了研究区域性桥梁的抗震优化问题,针对城市桥梁网络的震后修复优先级,引入基于交通密度的网络碎片化分区方法(FaDPa),提出了考虑恢复性和经济性的双重韧性指标,并针对震后短时抢救以及长时修复的时段特征引入了分阶段优化方法,尤其在长时修复阶段基于不同的修复需求对其进行了分时期处理;在抢险救灾阶段和长时修复阶段分别融入碎片化理论,前者以恢复韧性、时间为目标对抢救顺序进行优化,后者以综合韧性、碎片恢复性、时间对修复顺序进行优化。研究结果表明:基于密度的碎片化理论对桥梁网络不同修复阶段的地震损伤程度做出了不同的划分,此基础上展开的分阶段修复工作在抢险救灾过程中对其综合韧性提升程度达到52.3%,在长期修复过程中不影响韧性优化的前提下增加了碎片恢复性,其功能水平提升可达20.3%;修复优化阶段,经过考虑不同修复方向的双重韧性指标以及分时期处理的优化理论可以根据决策者的需求进行灵活调整,且面临不同修复环境时都具有一定的适应性。
Abstract:In order to study the seismic restoration of regional bridges, aiming at the post-earthquake repair priority of urban bridge networks, a network fragmentation partitioning method (FaDPa) based on traffic density was introduced, and a dual toughness index considering recovery and economy was proposed, and a phased optimization method was introduced according to the time period characteristics of short-term rescue and long-term restoration after earthquake, especially in the long-term restoration stage based on different restoration needs. The fragmentation theory was applied to the rescue and relief stage and the long-term repair stage respectively. The former optimized the rescue order with recovery toughness and time as the target, while the latter optimized the repair order with comprehensive toughness, debris recovery and time. The result shows that the fragmentation theory proposed makes different divisions based on density for the seismic damage degree of different repair stages of the bridge network. The staged repair work on this basis has improved its comprehensive toughness by 52.3% in the process of emergency rescue and disaster relief. Under the premise of not affecting the toughness optimization in the long-term repair process, the fragmentation resilience is increased, and its functional level is increased by 20.3%. In the repair optimization stage, the dual toughness index considering different repair directions and the optimization theory of time-phase processing can be flexibly adjusted according to the needs of decision makers, so that it can adapt to different repair environments, and the repair results considering fragmentation theory supplement the reliability of repair from different dimensions.
-
桥梁作为路网中枢发挥着举足轻重的作用。桥梁为主的城市交通抗震韧性[1-4],国内外学者主要在预防性(为应对地震到来预先对桥梁进行加固改造)、应对性(针对震时交通网络功能可靠性的应急方案)、可恢复性(使震后受损的桥梁网络恢复其原有状态的能力)、经济性(应对交通网络抗震的成本消耗与可持续发展)等方面展开研究。
分析国内外研究可知,BOCCHINI等[5]基于韧性最大化和成本最优提出了极端事件下桥梁修复策略优化框架;KARAMLOU等[6]利用遗传算法建立了桥梁网络关键位置修复时间以及韧性最大化的修复计划方法,提高了求解质量和效率;EDRISSI等[7]提出了一种基于救援行动效率的可靠性度量方法,证明了改进的网络可以有效减少灾害死亡人数;刘振亮[8]在分析了路段重要性以及功能损失的基础上,应用地震前后交通功能变化分析桥梁路网韧性;ZHANG等[9]综合考虑网络拓扑、冗余、流量、损坏程度和可用资源,提出了基于总恢复时间(TRT)和恢复轨迹偏差(SRT)的韧性修复框架;ANWAR等[10]提出了一种基于密度的道路网络快速分区方法,不仅考虑到了路网本身的结构特征,而且融入了交通密度的概念;侯本伟等[11]考虑介数、连通概率、灵敏度以及路网通行时间,利用逼近理想排序法(TOPSIS)确定路网单元重要度;ZOU等[12]基于粒子群优化算法分别实现了上层的最优资源分配和下层的动态交通分配模拟的双层决策框架,得到了成本效益有效提升的修复策略;KAVIANI等[13]针对区域路网的长期恢复规划问题提出了一种调度模型,采用分枝定界算法评估OD对之间的需求中断,实现了社会以及经济的韧性提升;吕彪等[14]提出以日变交通配流(DTA)为基础的城市道路网络韧性评估模型,通过对比用户均衡(SUE)模型,发现准确的韧性指标源自更准确的出行者行为决策和配流模型;LIU等[15]基于启发式算法建立了网络韧性评价方法,得到的优化修复顺序可以显著提高网络恢复的速度和效率;寇峥等[16]基于受损桥梁网络不同恢复过程的剩余功能、修复时间、可恢复性和震后经济损失进行优化,得到了基于多目标优化的修复优先级模型;宗成才等[17]通过随机模拟修复资源分配求得燃气管网在每次模拟破坏工况下的实时修复进程,用以求解震后性能、修复速率和恢复力等指标;张望欣等[18]提出了基于地震灾害管理的桥梁网络韧性决策框架,将地震周期划分为预防养护、应急救援与恢复使用三个阶段,结合遗传算法对桥梁网络的震后修复顺序进行优化;ZHANG等[19]提出了总恢复时间和累积收益率来衡量恢复过程中网络的系统恢复性,应用遗传算法进行决策分配;LIU等[20]开发了一种基于人工神经网络的方案,探索了多维功能恢复向量,以量化桥梁网络维护整体系统功能;SHARMA等[21]基于多目标优化问题提出了一种恢复过程的多尺度模型,旨在根据所提出的指标提高区域韧性,同时最小化恢复成本;缪惠全等[22]基于供水管网震后恢复的典型过程,提出了供水管网地震灾后恢复的阶段特征,并建立了供水管网动态抗震韧性评估方法。随着城市交通网络的规模不断增大,其复杂性也随之增加。众多学者基于此提出了交通网络的简化分析,即分区域处理,而因地震引起的桥梁功能损失将使网络区域化特征更加明显。在WANG等[23]的文章中,网络被定义为受建筑物倒塌或道路构件受损导致的路段堵塞,节点彻底断开链接而形成的碎片化交通网络。
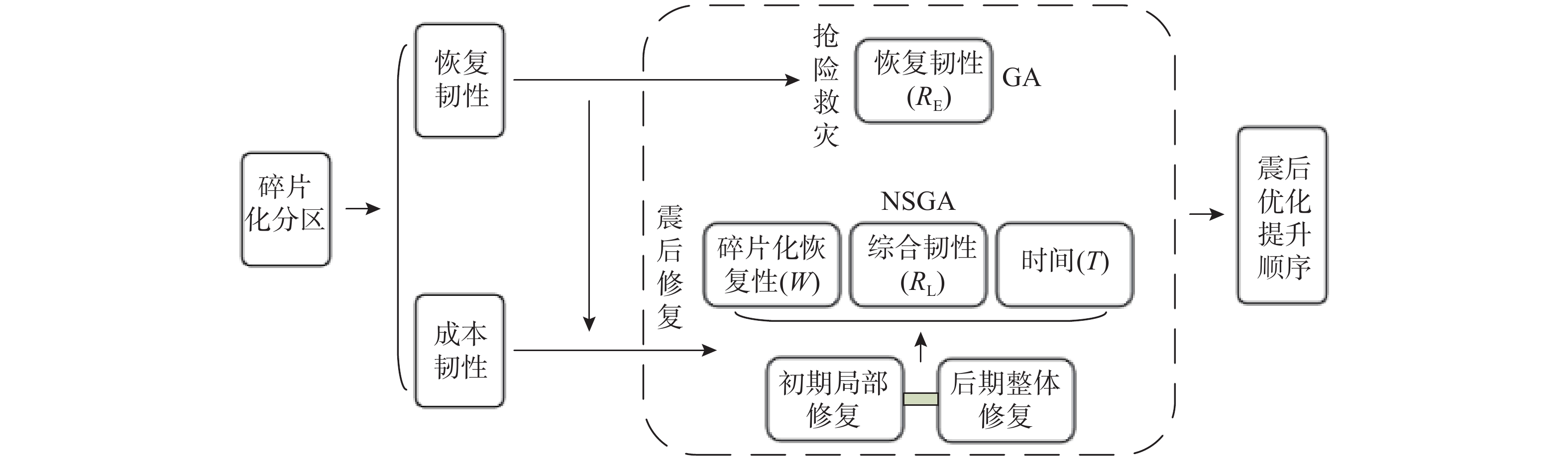
综上,国内外学者对于城市交通系统中桥梁网络的抗震性能研究已经取得了较为丰富的成果。然而,已有的研究仍然存在以下问题:1)现有的震后修复策略及框架聚焦于地震影响下桥梁路网的功能提升水平,对于地震造成的桥梁网络破坏形式的定义大多集中在其网络结构特性;2)现有韧性指标已然考虑了包括网络功能以及结构特性在内的多种影响因素,但对于修复过程中的韧性利用还有待提升。虽然当前对桥梁网络、交通网络地震破坏状态的研究相对较多,但是本文从网络动态特性入手,提出了基于交通密度的网络受震评价方法;本文在以复杂网络分析桥梁路网交通的基础上,引入基于密度的网络碎片化分区理论并对震后桥梁修复框架做出新的定义,基于震后修复过程的恢复性能以及修复过程中的成本利用状况,提出了综合考虑可恢复性以及经济性的双重韧性指标,最终建立了基于碎片化分区的桥梁网络震后修复优先级分析与优化方法,如图1所示。
1 城市桥梁网络
1.1 建立拓扑结构
采用主方法建立桥梁网络拓扑结构,然后对一次拓扑图进行对偶转化,构成以路段为节点,交叉口等其它交通汇集处为路段间链接的二次网络拓扑结构图。
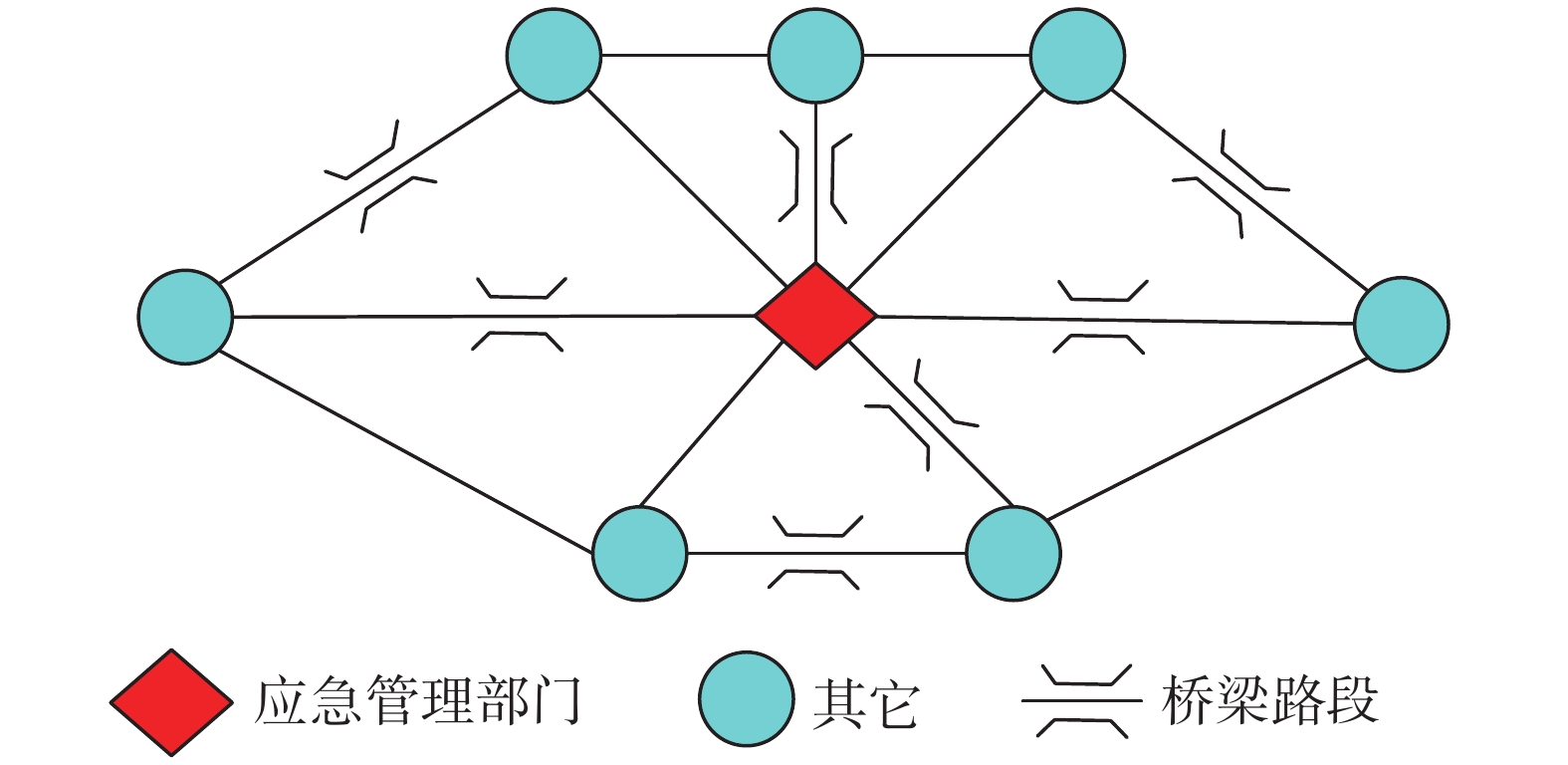
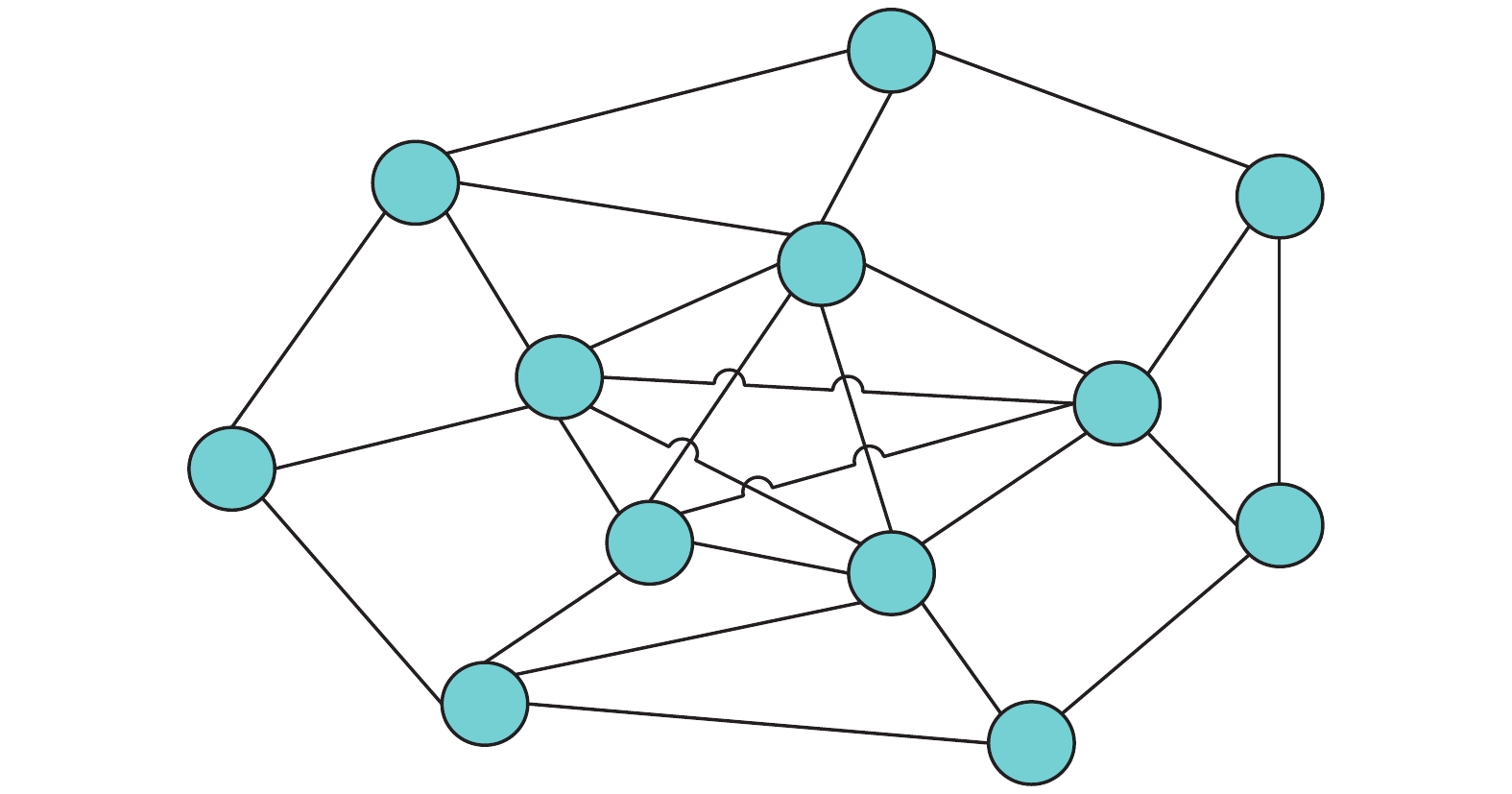
基于主方法建立的网络中,将交通汇聚处(紧急疏散区、应急救援区、居民生活区、道路交叉口)、应急管理部门定义为拓扑网络节点G={Ge,Gn},其中1⩽。将各路段定义为节点连边V = \left\{ {{G^i},{G^j}|{G^i},{G^j} \in G} \right\}。在二次拓扑中,节点与连边的定义发生转换,即节点G' = \left\{ {v({g_i},{g_j})|v \in V} \right\},当某条路段包含桥梁时,连边V' = \left\{ {g({v_i},{v_j})|g \in G} \right\}。以上因素共同构成了桥梁网络的拓扑结构,如图2和图3所示。
1.2 震后网络碎片化分区
不同地震烈度对桥梁的破坏作用并非绝对断路,而是伴随桥梁功能损伤基础上的路段通行能力不同程度下降。因此,本文采用FaDPa将网络拓扑特性、路网交通密度以及通行能力损失结合对桥梁网络地震前后区域化做出了新的定义。
1.2.1 碎片指标
当对桥梁网络进行碎片化处理时,由于分析对象为各路段,故采用二次拓扑网络进行分析。首先基于道路密度定义以下指标:
1)节点交通密度( {G'_i}.f ):在二次拓扑结构图中,将节点所表示的路段赋予交通密度,即:
{G'_i}.f = \frac{{{N_i}}}{{{W_{{G_i'}}}}} (1) 式中:{N_i}为某时刻路段{G'_i}上所有车辆数目;需要注意的是,在有关密度的分区中,因为融入了桥梁的有关能力,故{W_{{G'_i}}}为该路段的有效长度,在该路段无桥梁结构时为其物理长度,有桥梁结构时为受桥梁损伤引起的道路有效长度。
2)节点间距离({\rm{dist}}( {{G'_i},{G'_j}} )):假设其各节点的密度基于高斯分布且由高斯相似度来表示,其表达式为:
{\rm{dist}}({G'_i}^{},{G'_j}) = 1 - {\rm{sim}}({G'_i},{G'_j}) (2) 式中,{\rm{sim}}( {{G'_i}.{G'_j}} )为节点( {{G'_i}.{G'_j}} )之间所有可能连接关系的高斯相似度,经由路径的长短调和计算,得表达式为:
{\rm{sim}}({G'_i},{G'_j}) = \frac{{\displaystyle\sum\limits_{m = 1}^n {\dfrac{{{{g{\rm{si}}}}{{{{\rm{m}}}}^m}({G'_i},{G'_j})}}{n}} }}{{\displaystyle\sum\limits_{m = 1}^n {\dfrac{1}{m}} }} (3) 式中:m为节点({G'_i},{G'_j})之间可能存在的路径长度,即从 {G'_i} ~{G'_j}需要经过的路段数;{{g{\rm{si}}}}{\rm{m}}({G'_i},{G'_j})可由式(4)~式(6)得到。
{{g{\rm{si}}{{\rm{m}}}}^1}({G'_i},{G'_j}) = \exp \left( {\frac{{ - {{({G'_i}.f - {G'_j}.f)}^2}}}{{2 \times {\sigma ^2}(i,j)}}} \right) (4) \begin{split} & {{g{\rm{si}}{{\rm{m}}}}^2}({G'_i},{G'_j}) = \frac{1}{{{g^2}({G'_i},{G'_j})}} \times \\&\qquad \left( {\sum\limits_{{G'_k} \in ({G'_i},{G'_j})}^{} {( {{{g{\rm{s}}{\rm{i}}{{\rm{m}}}}^1}({G'_i},{G'_k}) \times {{g{\rm{si}}{{\rm{m}}}}^1}({G'_k},{G'_j})} )} } \right) \end{split} (5) \begin{split} & {{g{\rm{si}}{{\rm{m}}}}^n}({G'_i},{G'_j}) = \frac{1}{{{g^n}({G'_i},{G'_j})}} \times \\&\qquad \Bigg( \sum\limits_{( {{G'_{k1}},{G'_{k2}}, \cdots ,{G'_{k(n - 1)}}} ) \subset ({G'_i},{G'_j})} ( {{g{\rm{si}}{{\rm{m}}}}^1}({G'_i},{G'_{k1}}) \times\\&\qquad {{g{\rm{si}}{{\rm{m}}}}^1}({G'_{k1}},{G'_{k2}}) \times \cdots \times {{g{\rm{si}}{{\rm{m}}}}^1}({G'_{k(n - 1)}},{G'_j}) ) \Bigg) \end{split} (6) 式中:{{ g{\rm{si}}{{\rm{m}}}}^n}( {{G'_i}.{G'_j}} )为节点间路径长度为n时的高斯相似度;{g^n}( {{G'_i}.{G'_j}} )为节点间路径长度为n时的路线数目;{\sigma ^2}( {i,j} )为节点密度相对于节点密度平均值\mu 的方差,其公式为:
{\sigma ^2}(i,j) = \frac{1}{{{n_{G'}}}} \times \left( {\sum\limits_{i = 1}^{{n_{G'}}} {{{\left( {{G'_i}.f - \mu } \right)}^2}} } \right) (7) 3)节点距离阈值(\kappa ):由每个节点与周围直接连接节点的高斯相似度给出定义:
\kappa = 1 - \frac{1}{{| {{\rm{link}}( {{G'_i}} )} |}} \times \sum\limits_{{G'_i} \in {\rm{link}}( {{G'_j}} )} {{\rm{sim}}( {{G'_i},{G'_j}} )} (8) 式中,|{\rm{link}}\left( {{G'_i}} \right)|表示直接与{G'_i}链接的节点个数。
4)局部密度(\rho \left( {{G'_i}} \right)):比预定义的距离阈值到{G'_i}距离更小的节点数目,其表达式为:
\rho ( {{G'_i}} ) = \sum\limits_j^{} {\Delta ( {{\rm{dist}}( {{G'_i},{G'_j}} ) - \kappa } )} (9) 式中,\Delta \left( x \right) = \left\{ \begin{aligned} &1,\;\;x < 0 \\& 0,\;\;x \geqslant 0 \end{aligned} \right.为分段函数。
5)高密度距离(\delta \left( {{G'_i}} \right)):从节点{G'_i}到局部密度较高的节点{G'_j}最近的距离,其表示为:
\delta ( {{G'_i}} ) = {{\max}_{\forall G':\rho ( {{G'_j}} ) > \rho ( {{G'_n}} )}}{\rm{dist}}( {{G'_i},{G'_j}} ) (10) 若某个节点拥有高密度距离节点,则将其定义为此节点的密度父节点,此节点即为其密度子节点;而当某个节点无密度父节点时即为密度峰值节点(DPN)。
1.2.2 碎片化形成
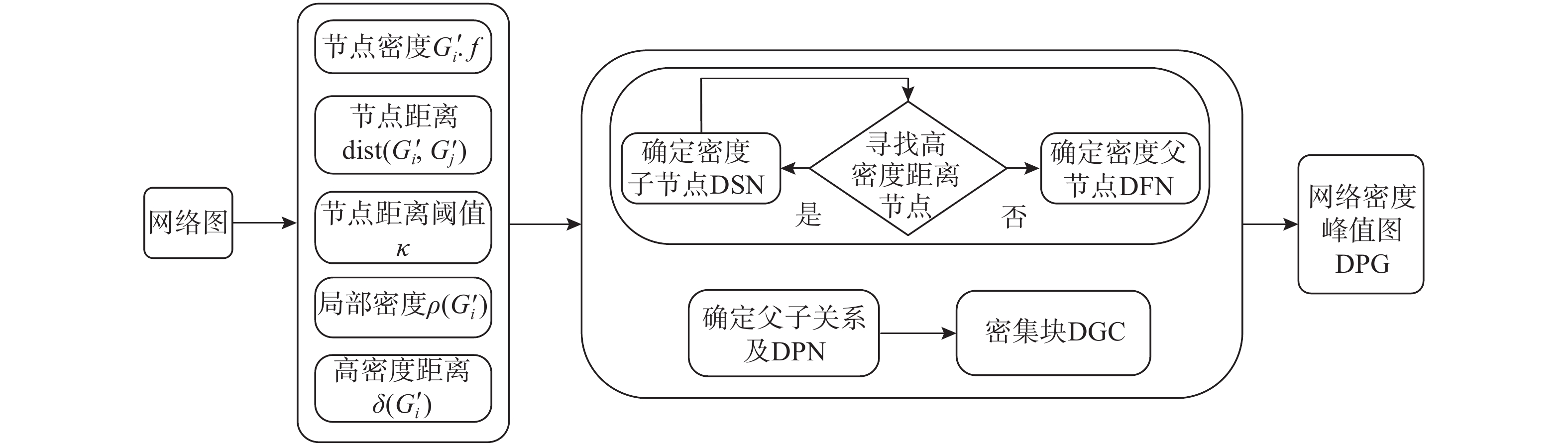
通过1.2.1节对基于交通密度的碎片化基础定义以及文献[10]中对FaDPa方法的说明,以MATLAB软件建立模型,得到如图4所示网络碎片化形成框架图。由图4可知,在该模型中,首先计算网络中各节点有关变量,而核心步骤为寻找节点间的密度父子关系,再确定此类节点间密度峰值节点(DPN),即可在网络上形成各节点的密集块(DGC)聚类,多个密集块共同构成网络密度峰值图(DPG)。
如图5所示为网络碎片形成的过程,其中图5(a)表示一个网络简图,每个节点都有相应的节点密度,表1则描述了各节点间的距离,假设距离阈值\kappa =0.5,加粗部分表示其节点间距离小于\kappa ;图5(b)中的深色节点代表DPN,实线表示两节点具有父子密度关系,虚线表示节点的链接关系;图5(c)中用虚线包围起来的部分各表示一个密集块DGC,实线链接表示各DGC之间的邻域关系;图5(d)即该网络形成的碎片化分区。建立网络碎片化分区模型,对城市桥梁网络图进行处理,即可得到碎片化的网络分区。
表 1 节点间距离Table 1. Distance between node节点 节点 局部密度 A B C D E F G H I J K L A − 0.89 − 0.89 − 0.10 − 0.95 − − − − 1 B 0.89 − 0.30 − 0.64 − 0.10 − − − − − 2 C − − − − − − − − 2 D − − − − − − − − 2 E − − − − 0.81 0.10 − 0.00 − 2 F 0.10 − 0.81 − 0.59 − − − 0.89 − 0.10 2 G − 0.10 − 0.10 − 0.89 − 0.30 − − − − 3 H 0.95 − 0.59 − 0.81 − 0.30 − − − − − 1 I − − − − 0.10 − − − − 0.10 − 0.59 2 J − − − − − 0.89 − − 0.10 − 0.30 − 2 K − − − − 0.00 − − − − 0.30 − 0.30 3 注:加粗部分表示该节点间距离小于其距离阈值。 1.3 考虑可恢复性与经济性的网络综合韧性指标
为了评估优化策略的先进性,同时考虑经济性与可恢复性,定义策略综合韧性指标为修复时间内修复成本与网络性能的综合水平。采用文献[1]提出的韧性三角型框架得到两者计算公式分别为:
{R^{\rm{Q}}} = \int_0^T {\frac{{Q(t)}}{T}} {\rm{d}}(t) (11) R^{\psi} = \int_0^T {\frac{{\psi (t)}}{T}} {\rm{d}}(t) (12) 式中,Q\left( t \right)为桥梁网络系统功能函数,计算公式为:
Q(t) = \frac{{\omega (t) - {\omega ^{\rm{e}}}}}{{{\omega ^{\rm{p}}} - {\omega ^{\rm{e}}}}} (13) 式中,\psi \left( t \right)为成本利用情况,计算公式为:
\psi (t) = \frac{{(\omega (t) - {\omega ^{\rm{e}}}){M^{\omega (t)}}}}{{({\omega ^{\rm{p}}} - {\omega ^{\rm{e}}}){M^{\rm{p}}}}} (14) 两者均作为衡量韧性的指标,其中\omega \left( t \right)为修复活动达到t时刻的网络性能;{\omega ^{\rm{e}}}为网络性能最低时刻(震后未经修复时);{\omega ^{\rm{p}}}为震前网络的完整性能;{M^{\omega \left( t \right)}}为网络经修复性能达到\omega \left( t \right)时消耗的成本;{M^{\rm{p}}}为从修复开始到结束所消耗的成本。需要注意的是,桥梁的修复成本由桥梁受损状况以及新建费用确定。
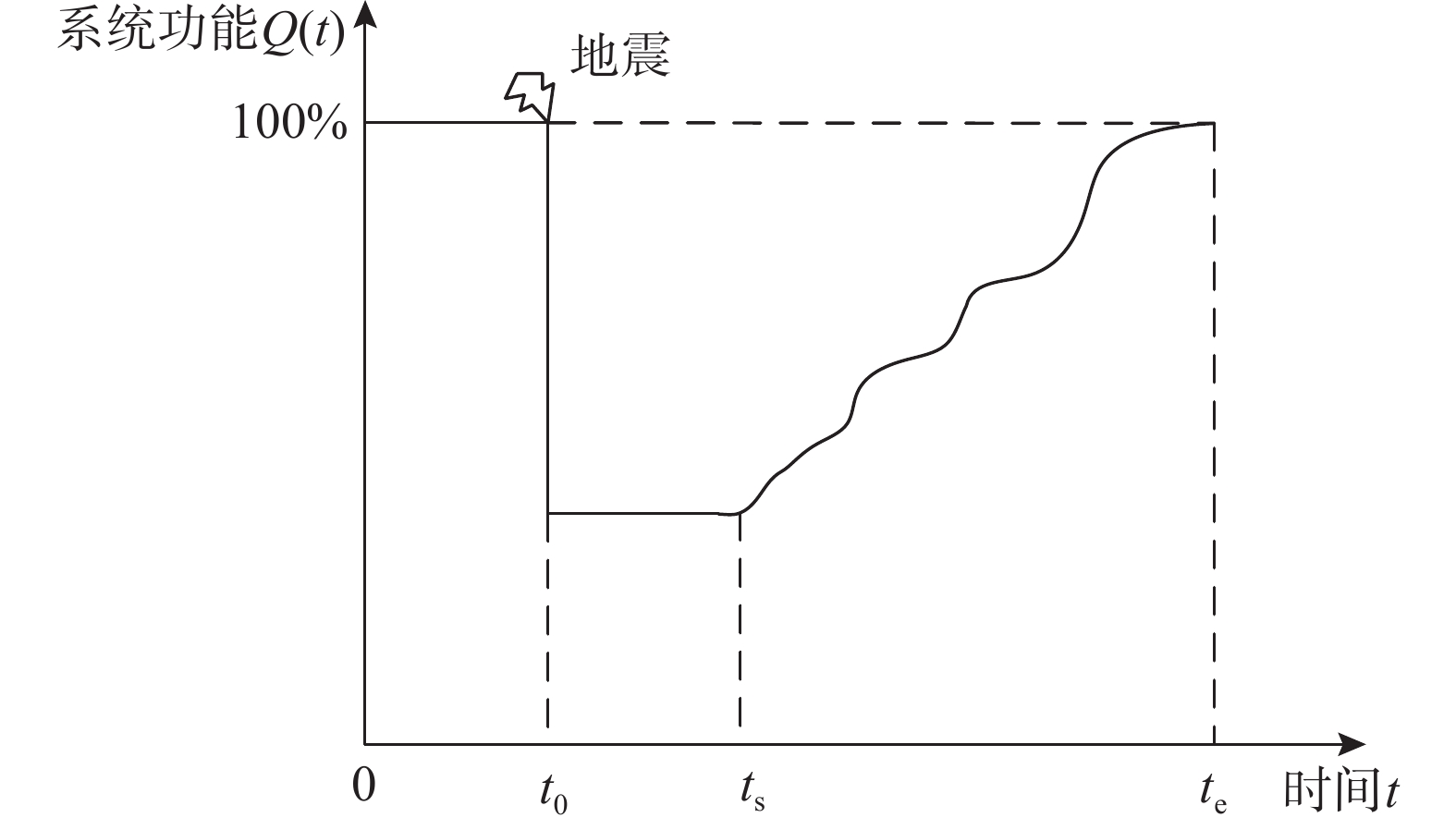
如图6所示为网络系统功能变化状况,图6中: {t_0} 时刻发生地震;{t_{\rm{s}}}时刻开始修复工作;{t_{\rm{e}}}时刻修复结束。因此桥梁网络修复活动的综合韧性为:
R = {\delta _{\rm{Q}}} \times {R^{\rm{Q}}} + {\delta _{\psi} } \times {R^{\psi} } (15) 式中, {\delta _\rm{Q}} 与 {\delta _\rm{\psi} } 分别为成本韧性与性能韧性的权重调整系数,且 {\delta _\rm{Q}} + {\delta _\rm{\psi} } = 1 。
2 震后修复策略
在震后桥梁网络的整个修复时期,整体网络的通行需求以及网络功能是随着桥梁的修复工作持续改变的,因此沿用文献[18]提出的决策框架以应对震后不同时期的修复工作对优化策略进行分阶段处理。
2.1 抢险救灾阶段
在地震发生后的初始期,由政府下达的应急救援命令将被立即执行。而由于桥梁功能受损,整体网络的连通性将发生改变,桥梁修复工作的目标是恢复网络部分通行能力并降低网络碎片化程度,同时恢复应急管理节点的交通功能,提升救援效率。此阶段的修复方法为架设应急通行设施或开辟应急通行道路,修复策略优化方向应当为:
1)减少修复时间,提升救援效率;
2)降低碎片化,减少整体网络碎片化数量,提升整体连通性,便于开展救援管理工作;
3)提升韧性。
在降低网络碎片程度的基础上,定义网络的功能指标为所有应急管理节点的救援能力之和与碎片化分区地震前后相似性之积,其表达式为:
{\omega _{\rm{E}}}(t) = DS(t) \times \sum\limits_{m = 1}^e {{\eta _m} \times C{O_m}(t)} (16) 式中:DS\left( t \right)为修复进行到t时刻桥梁网络碎片化分区相对于震前的相似性;{\omega _{\rm{E}}}\left( t \right)为网络t时刻的救援能力;{D^0}、{D^1}分别为地震前后桥梁网络的碎片化数量;{\eta _m}为应急节点m失效时的网络效率损失量占所有应急节点的归一化权重;C{O_m}\left( t \right)为t时刻应急节点m与所有非应急节点的连通度均值。其计算式如下:
C{O_m}(t) = \frac{1}{{n - e}}\sum\limits_{i = 1}^{n - e} {{k_{mi}}} (17) 式中:{d_{ij}}为节点之间最短路径;{k_{mi}}为应急节点m与普通节点i之间的连通度,其数值为使两者不连通所需要移除的最小边数目。
碎片化分区相似性由密度峰值节点决定,计算公式为:
DS(t) = \left\{ \begin{aligned} & \frac{{{C_{\rm{D}}}(t)}}{{C_{\rm{D}}^0}},\qquad\qquad\;\;{C_{\rm{D}}}(t) < C_{\rm{D}}^0 \\ & 1 - \frac{{{C_{\rm{D}}}(t) - C_{\rm{D}}^0}}{{C_{\rm{D}}^0}},\;\;\;\;C_{\rm{D}}^0 \in {C_{\rm{D}}}(t) \end{aligned} \right. (18) 式中:C_{\rm{D}}^0为震前碎片分区中DPN的数目;{C_{\rm{D}}}\left( t \right)为t时刻碎片分区中含有与震前相同DPN的数目。需要注意的是,由于本阶段仅针对部分桥梁修复,故碎片化分区过程不考虑桥梁损失引起道路有效长度变化。
联立式(16)~式(18)得到功能指标为:
{\omega _{\rm{E}}}(t) = DS(t) \times \sum\limits_{m = 1}^e {\left( {\frac{{{\eta _m}}}{{n - e}} \times \sum\limits_{i = 1}^{n - e} {{k_{mi}}} } \right)} (19) 由于此时的修复工作为应急救援状态,因此不考虑成本消耗,联立式(13)、式(15)和式(21)即得到本阶段的韧性指标{R_{\rm{E}}}。本阶段实际上为车间调度(GA)问题[24],其优化目标为:
\max \left( {{R_{\rm{E}}}} \right) (20) 约束条件为:
\left\{ \begin{gathered} E{R_{\rm{b}}}\overrightarrow {{C_{\rm{b}}} {\geqslant} 75\text{%} } E{R_{{\rm{b}} + 1}} \\ {B_{\rm{t}}} \leqslant {W_{\rm{t}}} \\ \end{gathered} \right. (21) 其中,通行能力受损大于25%桥梁必须采取应急措施,当某座桥梁的通行能力保持在75%以上时,仍然具备良好通达性,不对其做应急处理;某一时刻同时修复的桥梁数{B_{\rm{t}}}不应大于修复队伍{W_{\rm{t}}}。
2.2 震后修复阶段
在桥梁修复阶段,桥梁网络的通行需求不断发生变化,且由于修复时间较长,需要考虑的因素增多。在保证震后修复资源最大化利用的前提下,此时的桥梁网络修复特征如下:
1)桥梁修复困难,持续时间较长;
2)桥梁材料昂贵,修复所需资金庞大;
3)网络碎片化分区变异明显,且由于修复周期较长,需单独考虑;
4)综合考虑1)~3),经济重心所在区域的桥梁应处于优先级修复次序;
5)在保证网络结构特性的同时,应当考虑整体网络的通行能力。
综合考虑以上修复特征,将本阶段的修复优化进行分时期处理,初期针对网络重点区域进行修复,后期则考虑网络整体性能进行修复;利用NSGA-Ⅱ算法,优化指标定义为综合韧性({R_{\rm{L}}})、碎片化分区恢复性(W)以及修复时间(T)。
修复初期,优先对城市桥梁网络中的重点区域桥梁展开修复工作;使用层次分析法[25],基于震前网络碎片分区的交通密度、修建费用以及边介数对其重要性进行划分;定义修复时的功能指标为网络效率,采用一次拓扑网络进行分析。由于桥梁损伤不一定造成道路直接丧失连通性,而是不同程度的通行能力损失;因此,基于文献[26-27]桥梁通行能力损伤折减,定义新的网络效率。其表达式为:
\begin{split} \omega _{\rm{L}}^{\rm{s}}\left( t \right) = & \frac{1}{{N\left( {N - 1} \right)}} \times \\ & \sum\limits_{i,j \in N \cap i \ne j} {\left( {\frac{1}{{{d_{ij}}\left( t \right)}} \times \left( {1 - \mathop {\max } \left( {{\xi _{ij}}} \right)} \right)} \right)} \end{split} (22) 式中:N为网络中所有节点数目;{d_{ij}}为节点i、j之间最短距离;{\xi _{ij}}为i、j间最短路径上某一路段的通行能力损失率,见表2。
表 2 桥梁震后能力损伤Table 2. Capacity damage of bridge after earthquake损伤等级 通行能力损失率\xi 未破坏(N) 0.00 轻微破坏(L) 0.00 中度破坏(M) 0.25 严重破坏(E) 0.50 基本倒塌(C) 1.00 修复后期,重在解决城市桥梁网络出行问题,提升道路网络整体功能水平。定义其功能指标为桥梁网络通行总里程;表达式为所有路段的有效通行长度与交通流乘积的累计,即:
{\omega _{\rm{L}}} = \sum\limits_{l \in G} {a\left( l \right) \times \lambda \left( l \right)} (23) 式中,路段上的交通流量\lambda \left( l \right)由容量限制-增量交通配流模型[8]进行动态配流得到。道路有效长度a\left( l \right)的值被定义为受路段上桥梁的损伤状态影响的道路有效通行距离,表达式为:
a\left( l \right) = a_l^0 \times \left[ {1 + \alpha {{\left( {\frac{{{q_l}}}{{{C_l}}}} \right)}^\beta }} \right] (24) 式中:a_l^0为路段l本身物理长度;{q_l}为路段l上的实际交通流;{C_l}为桥梁的实际通行能力;\alpha 、\beta 为模型参数,取\alpha = 0.15,\beta = 4。将式(24)代入式(23)可得到桥梁网络通行总里程的最终表达式为:
{\omega _{\rm{L}}} = \sum\limits_{l \in G} {\lambda \left( l \right) \times a_l^0 \times \left[ {1 + \alpha {{\left( {\frac{{{q_l}}}{{{C_l}}}} \right)}^\beta }} \right]} (25) 综合考虑本阶段修复状况,将式(25)分别代入式(13)、式(14)即得到本阶段性能函数及成本利用情况为:
Q\left( t \right) = \left\{ \begin{aligned} & {Q^{\rm{s}}}\left( t \right) \\& {Q^{\rm{f}}}\left( t \right) \end{aligned} \right. = \left\{ \begin{aligned} & \frac{{\omega _{\rm{L}}^{\rm{s}}\left( t \right) - \omega _{\rm{L}}^{\rm{e}}}}{{\omega _{\rm{L}}^{{\rm{ps}}} - \omega _{\rm{L}}^{\rm{e}}}} \times {\sigma _{\rm{s}}},&& t \in [0,{T_{\rm{s}}}] \\ & {Q^{\rm{s}}}\left( t \right) + \frac{{\omega _{\rm{L}}^{\rm{f}}\left( t \right) - \omega _{\rm{L}}^{\rm{e}}}}{{\omega _{\rm{L}}^{{\rm{pf}}} - \omega _{\rm{L}}^{\rm{e}}}} \times {\sigma _{\rm{f}}},&& t \in [{T_{\rm{s}}},{T_{\rm{f}}}] \end{aligned} \right. (26) \begin{split} & \psi ( t ) = \left\{ \begin{aligned} & {\psi ^{\rm{s}}}( t ) \\& {\psi ^{\rm{f}}}( t ) \end{aligned} \right. = \\&\qquad \left\{ \begin{aligned} & \frac{{( {\omega _{\rm{L}}^{\rm{s}}( t ) - \omega _{\rm{L}}^{\rm{e}}} ){M^{\omega _{\rm{L}}^{\rm{s}}( t )}}}}{{( {\omega _{\rm{L}}^{{\rm{ps}}} - \omega _{\rm{L}}^{\rm{e}}} ){M_{{{{T}}_{\rm{s}}^{\rm{p}}}}}}} \times {\sigma _{\rm{s}}},\qquad\;\;\;\; t \in [ {0,{T_{\rm{s}}}} ] \\ & {\psi ^{\rm{s}}}( t ) + \frac{{( {\omega _{\rm{L}}^{\rm{f}}( t ) - \omega _{\rm{L}}^{\rm{e}}} ){M^{\omega _{\rm{L}}^{\rm{f}}( t )}}}}{{( {\omega _{\rm{L}}^{{\rm{pf}}} - \omega _{\rm{L}}^{\rm{e}}} ){M_{{{{T}}_{\rm{f}}}}}^{\rm{p}}}} \times {\sigma _{\rm{f}}},\;t \in [ {{T_{\rm{s}}},{T_{\rm{f}}}} ] \end{aligned} \right. \end{split} (27) 式中:{T_{{\rm{s}}}} 、 {T_{{\rm{f}}}}分别为初、后期修复完成时刻; {\sigma _{{\rm{s}}}} 、{\sigma _{{\rm{f}}}} 分别为初、后期修复的权重调整系数。
联立式(11)、式(12)、式(15)、式(26)和式(27)即可得到本阶段综合韧性指标{R_{\rm{L}}}。
在此阶段内,网络的修复工作覆盖全部受损桥梁,故利用受桥梁损伤影响的道路有效长度(见式(24))重新处理网络碎片化分区;假设在桥梁修复过程中,其通行能力损伤率呈线性下降;利用修复全过程的碎片化相似性(见式(18))结合韧性三角形框架来刻画碎片化分区恢复性,其表达式为:
W = \int_0^{{T_{\rm{f}}}} {\frac{{DS\left( t \right)}}{{{T_{\rm{f}}}}}} {\rm{d}}t (28) 综上所述,本阶段的优化目标为:
\left\{ \begin{aligned} & \max \left( {{R_{\rm{L}}}} \right) \\& \max \left( W \right) \\& \min \left( T \right) \end{aligned} \right. (29) 3 算例分析
3.1 桥梁网络参数
本文选取某地桥梁网络为研究对象,由12个节点与17条道路构成,每条道路上均设有桥梁,其中5、9为应急救援节点。建立桥梁网络一次拓扑结构如图7所示,表3则为网络基本信息。桥梁损伤程度由地震易损性决定,参考文献[28]。
表 3 桥梁网络基本参数Table 3. Basic parameters of bridge network路段 节点 道路参数 地震参数 桥梁 桥梁参数 路长/km 均交通量(pcu/h) 基本通行能力(pcu/h) 类型 新建费用(百万元) 损伤程度 抢险时间/h 修复
时间/月通行能力损失率ξ 1 (1,2) 0.60 1226 1550 地震断裂带震中位置距路网较近,地震动为浅源地震,震源深度10 km 1 MSSS steel 20.38 E 10 4 0.50 2 (2,3) 0.60 1344 2340 2 MSSS steel 22.75 L − 1 0.00 3 (1,8) 0.60 857 1000 3 MSSS steel 23.45 E 10 3 0.50 4 (1,5) 0.70 984 490 4 MSSS steel 18.50 M − 2 0.25 5 (2,4) 1.00 1923 2340 5 MSSS steel 19.42 C 10 5 1.00 6 (3,4) 0.85 1264 1700 6 MSSS con 25.34 M − 2 0.25 7 (7,8) 0.85 1123 300 7 MSC steel 15.22 N − − 0.00 8 (6,7) 0.80 610 830 8 MSC steel 15.39 E 10 1 0.50 9 (4,5) 0.85 418 470 9 MSC steel 20.54 E 10 4 0.50 10 (8,9) 0.85 556 780 10 MSC steel 21.47 M − 2 0.25 11 (7,10) 0.80 398 500 11 MSC steel 30.05 C 10 5 1.00 12 (6,10) 0.60 536 350 12 MSC con 41.66 E 10 3 0.50 13 (6,11) 0.60 941 1100 13 MSC con 22.56 M − 2 0.25 14 (5,11) 0.60 1231 2340 14 MSC con 30.40 E 10 4 0.50 15 (5,12) 0.70 547 400 15 MSSS con 35.79 E 20 3 0.50 16 (9,10) 0.80 1238 2590 16 MSSS con 20.58 E 10 3 0.50 17 (11,12) 0.85 1024 1550 17 MSSS con 34.22 L − 1 0.00 注:MSSS steel为多跨简支钢梁桥;MSC steel为多跨连续钢梁桥;MSSS con为多跨简支混凝土梁桥;MSC con为多跨连续混凝土梁桥。 3.2 分析结果
3.2.1 碎片化
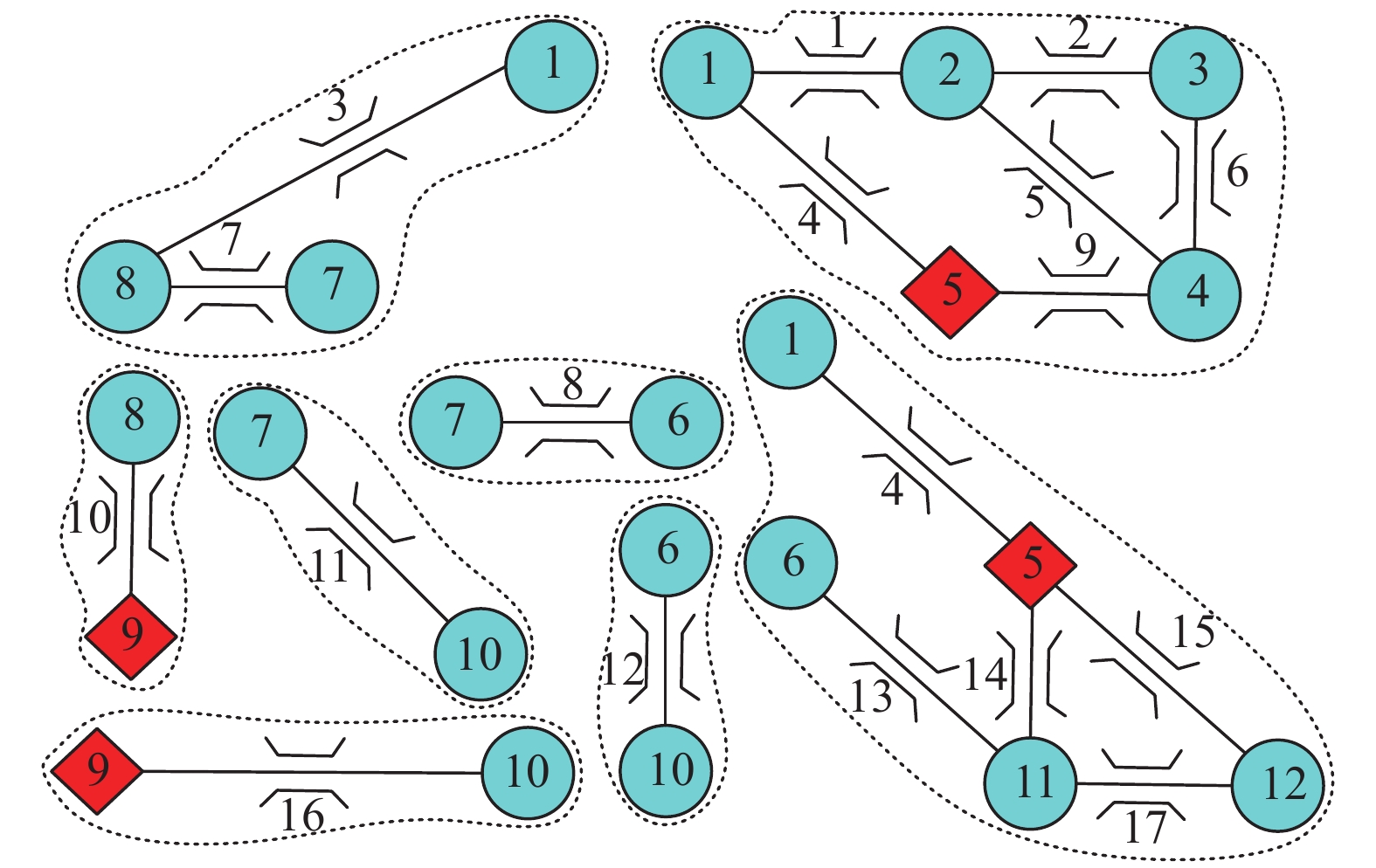
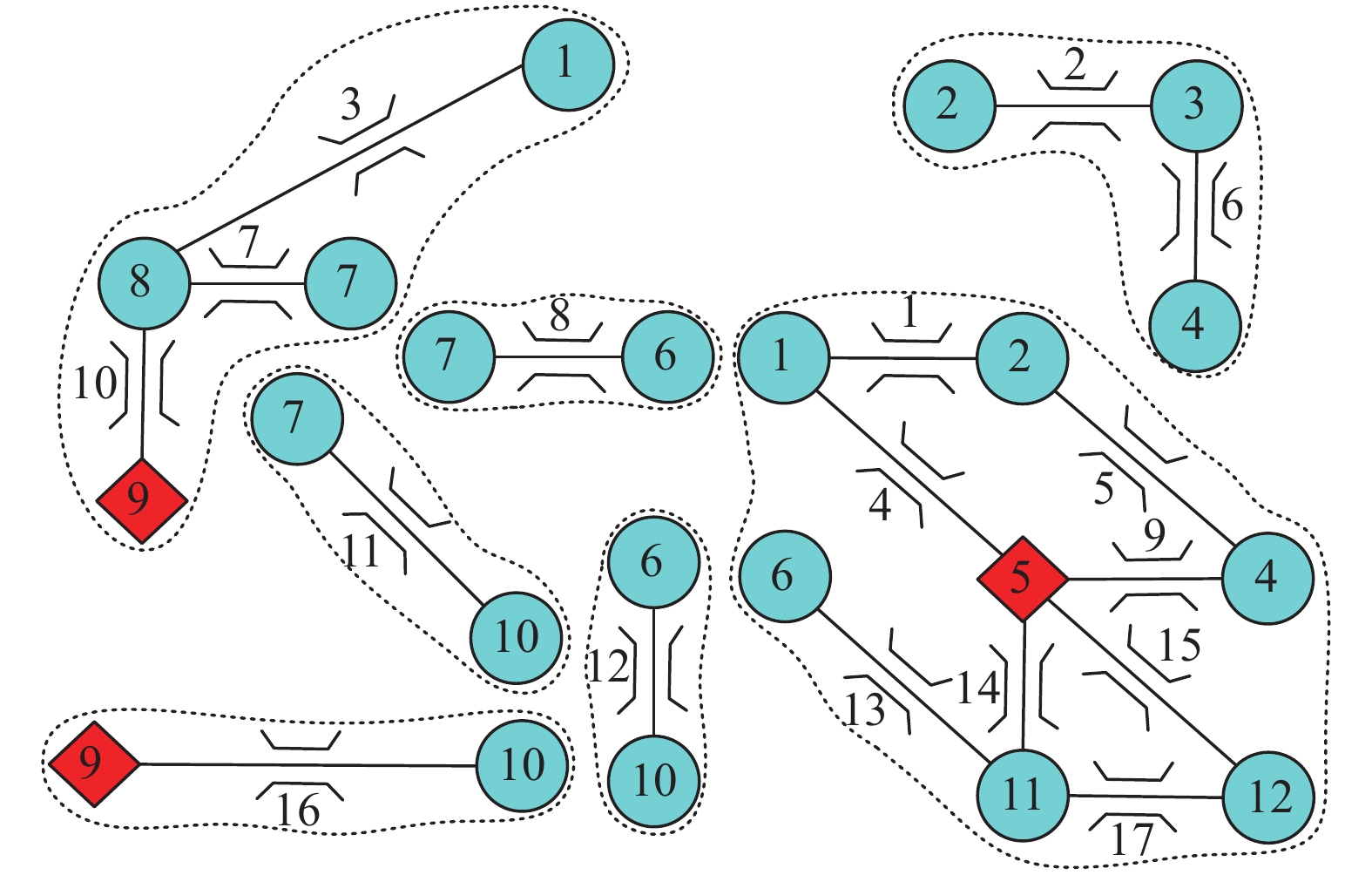
对桥梁网络进行碎片化处理,受限于网络大小,仅对其进行一级碎片化处理,图8、图9、图10分别给出了桥梁网络震前与震后两阶段的碎片化处理结果。
分析经历地震前后的碎片化分区结果可以发现,桥梁网络的道路聚类变化极大,网络碎片化分区明显减少;而如图9所示,经历抢险救灾阶段后的碎片分区又经历了较为明显的分区变化。这表明基于密度分析的碎片化分区方法对桥梁道路通行能力的改变比较敏感。
如表4所示为桥梁网络各时期碎片化分区状态,加粗部分表示各碎片的DPN。其中,震前网络由7个DGC组成,每个DGC中的DPN分别为道路3、5、8、10、11、12、14、16;震后抢险救灾前网络受桥梁损伤影响划分为5个分区,DPN分别为道路1、3、9、11,网络分区数量明显减少,这是由于震后大量路段通行状态为不连通,即道路有效长度无限大,道路交通密度无限小,从而引起的道路密度聚类;抢险救灾前的网络仅针对通行能力损失超过75%的桥梁,而在彻底修复之前,由于考虑到所有桥梁的损伤状况,故道路聚类发生改变,其DPN分别为3、6、8、11、12、14、16。
表 4 碎片化分区对比Table 4. Comparison of fragmented partitions震前 抢险救灾前 震后修复前 [3, 7] [1] [3, 7, 10] [1, 2, 5, 6, 9] [3, 7] [2, 6] [8] [2, 4, 5, 6, 9, 13, 14, 15, 17] [8] [10] [8, 10, 11, 12, 16] [11] [11] − [12] [12] − [1, 4, 5, 9, 13, 14, 15, 17] [4, 13, 14, 15] − [16] [16] − − 注:加粗部分为每个碎片的密度峰值节点DPN。 3.2.2 抢险救灾
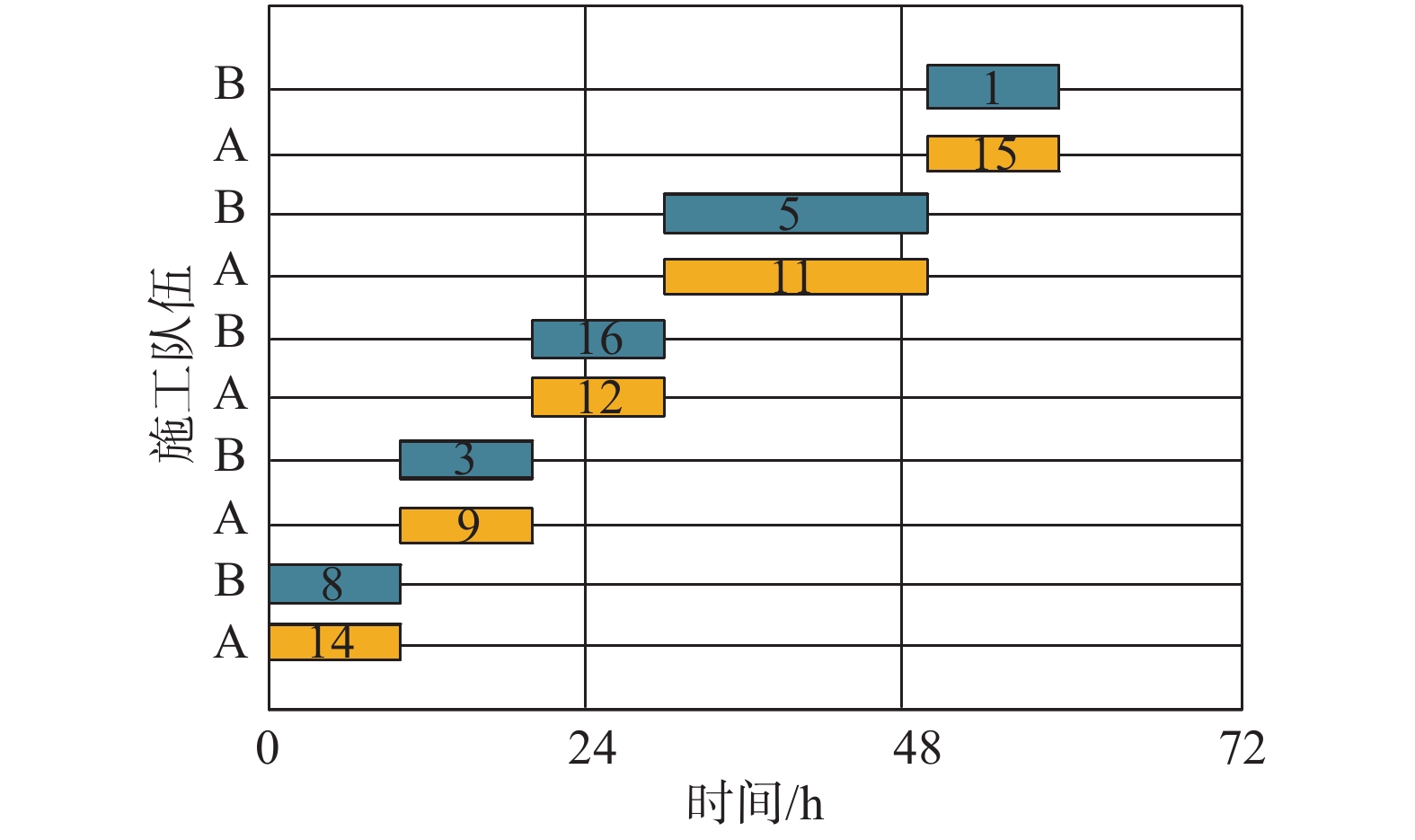
本阶段的应急工作由两个施工队同时进行,控制时间5 d,优化结果如图11、图12。如图11所示为经优化后的桥梁网络应急修复调度计划,由队伍A、队伍B共同进行施工,每个队伍在同一时间段只能救援一座桥梁,图11中框内号码为该时段处于修复状态的桥梁编号,经优化应急阶段修复时长可缩短至60 h。
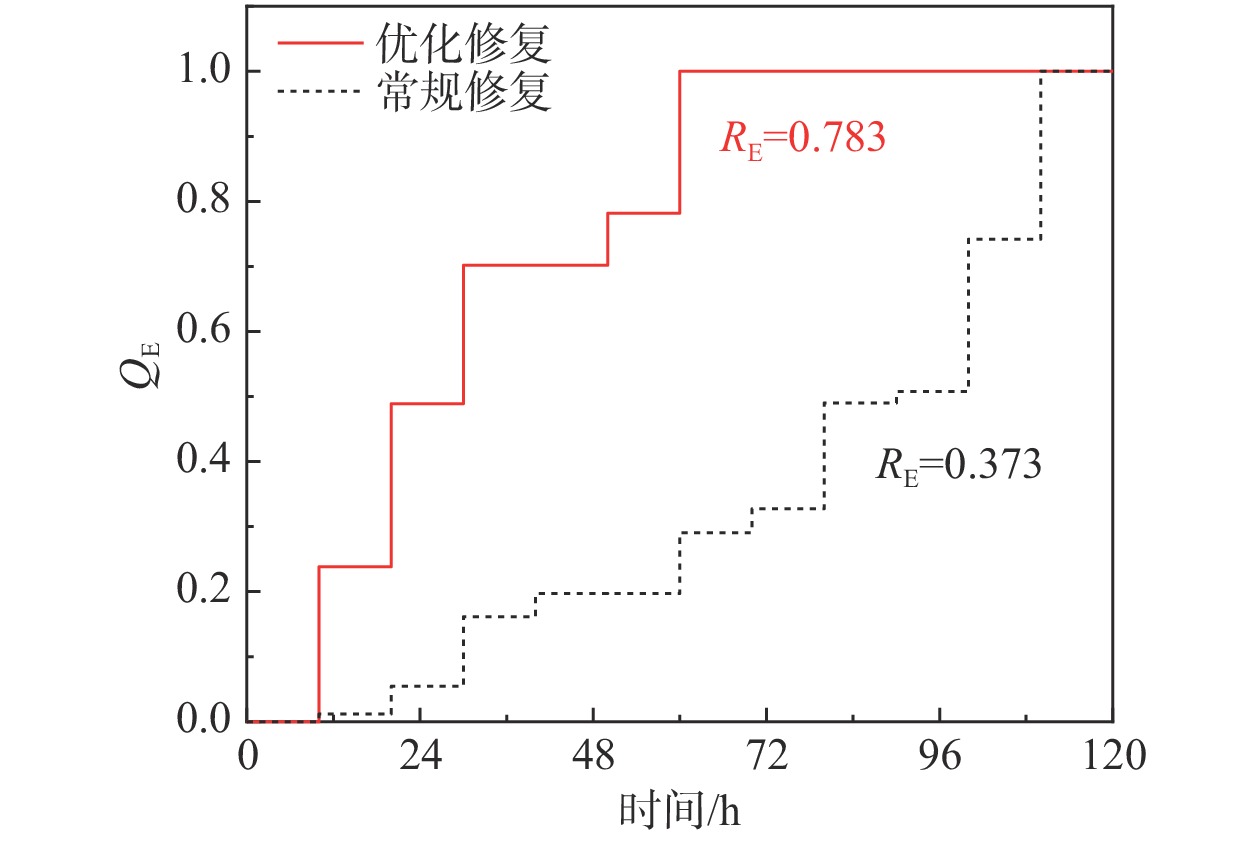
图12所示为经抢险救灾阶段的修复优先级模型优化后的桥梁修复策略与常规修复策略(不经调度优化的修复策略,随机选择桥梁进行修复,韧性低且耗时久)的系统性能对比图;经优化后的修复计划不仅显著提升了修复全过程的韧性,而且缩短了救援时间,提高了救援效率;经优化后的修复计划韧性提升了52.3%,提升效果明显;同样可以看出的是,优化结果整体韧性水平略低,这是未考虑震前的桥梁抗震加固以及碎片化相似性特点的合理水平,不对优化策略的性能造成影响,因此本文提出的应急阶段救援顺序优化方法是有效的。
3.2.3 震后修复
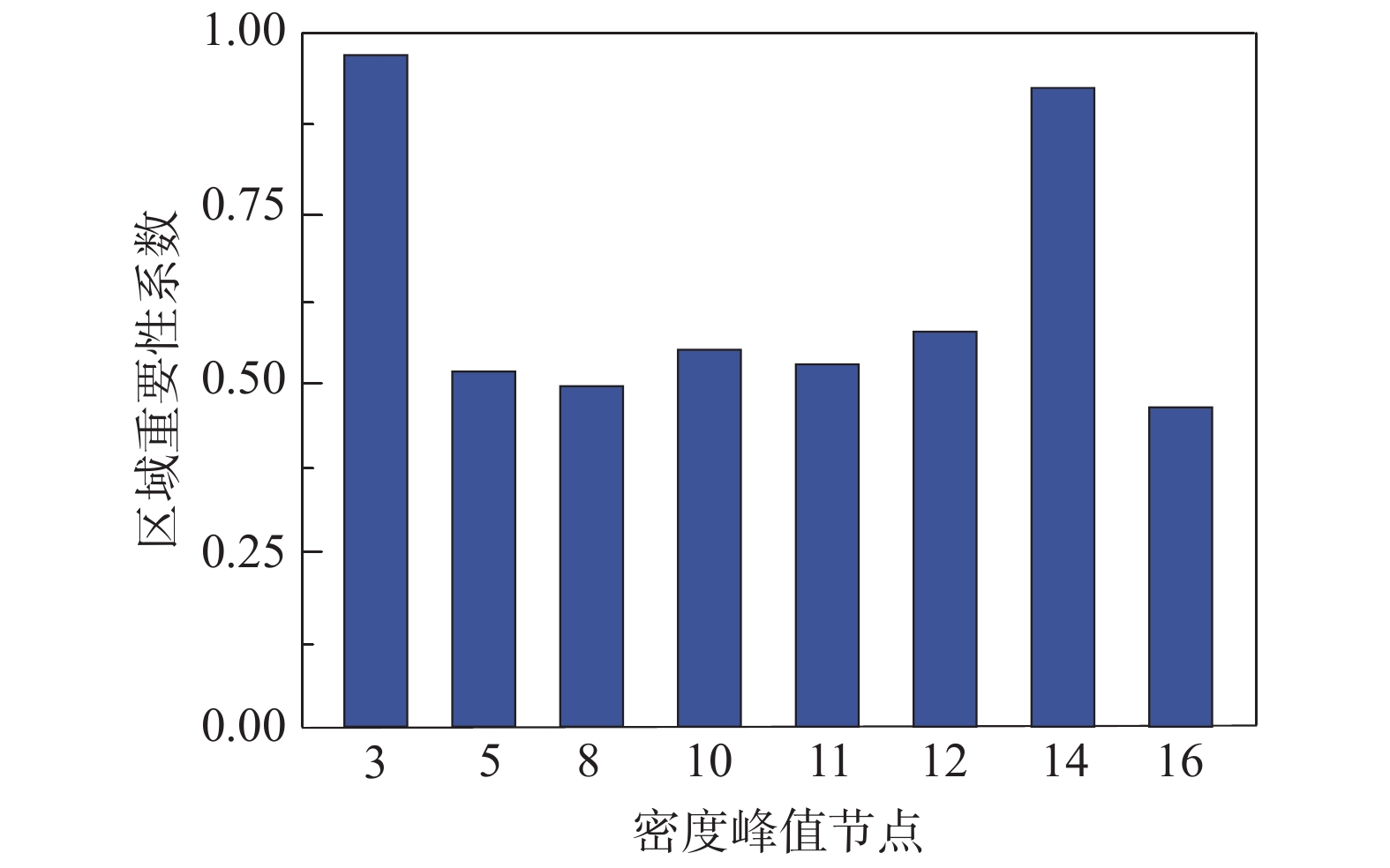
本阶段修复工作同时考虑修复初期与修复后期所占权重对修复计划的综合影响,首先根据层次分析法获得震前网络碎片化分区的重要性如图13所示。
在进行震后修复之前需对震前网络的碎片分区进行评价,为修复阶段的优化提供准备。如图13所示给出了震前桥梁网络各碎片化分区经其相应交通密度、新建费用、边介数结合层次分析法所得到的综合评价,可以看出密度峰值节点3和14的区域重要性系数最大,接近于1,其余的DPN的系数均动态趋近于0.5,所以重点分区是以3、14为DPN的网络碎片。对其修复时期以及综合韧性指标的权重系数分别进行调整可得到不同决策下的近似最优解。
如图14所示,图14(a)、图14(b)、图14(c)三图给出了修复时期调整系数为{{{\sigma _{\rm{s}}}} / {{\sigma _{\rm{f}}}}}=1,综合韧性指标调整系数分别为 {{{\delta _\rm{Q}}}/ {{\delta _\rm{\psi} }}} =1/4、1、4时的优化结果,随着韧性调整系数的增大(强调恢复性能),综合韧性指标的阈值相应变化为0.6、0.65、0.8,其提升程度分别为8.3%、23.1%,即恢复韧性对优化结果的影响明显大于成本韧性,且当恢复韧性占比大于成本韧性时提升程度更加明显,优化结果表现更好;而图14(d)、图14(e)、图14(f)三图则给出了综合韧性指标调整系数为 {{{\delta _\rm{Q}}}/ {{\delta _\rm{\psi} }}} =2/3,修复时期调整系数分别为{{{\sigma _{\rm{s}}}} / {{\sigma _{\rm{f}}}}}=1/4、1、4时的优化结果,随着时期调整系数的增大(强调初期修复),综合韧性指标阈值相应变化为0.45、0.6、0.77,提升程度分别为33.3%、28.3%,于是在强调初期修复时,优化结果表现更好。但碎片化恢复性的阈值并不随修复环境变化而变化。
为了展示震后修复优先级的具体结果,选取修复时期调整系数{{{\sigma _{\rm{s}}}} \mathord{\left/ {\vphantom {{{\sigma _{\rm{s}}}} {{\sigma _{\rm{f}}}}}} \right. } {{\sigma _{\rm{f}}}}}=1、综合韧性指标调整系数 {{{\delta _\rm{Q}}}/ {{\delta _\rm{\psi} }}} =1,而随机选取最终修复时间为17个月的桥梁修复顺序进行分析。如图15展示了修复时间在17个月的最终优化结果:16座受损桥梁在A、B、C三个修复队伍共同进行的修复工作中得到了理论最优的桥梁修复顺序,其碎片恢复性达到0.757,而此修复顺序在震后长时修复的三维优先级分析中仅是众多最佳修复顺序之一,多维的优先级优化中,其面对不同环境条件时的多样性同样突出。
随着修复环境的调整,震后修复框架整体表现出良好的适应性,在灵活修复的同时兼具稳定性。而通过对修复环境的不同模拟可以得到:在提出的方法中,强调初期修复以及恢复韧性而弱化成本韧性与后期修复可以得到更好的结果。同时为了更准确描述各优化指标间的关系,将以上优化结果分别投影到各二维平面如图16所示。
图16展示了不同优化系数下的二维优化结果。对比图16(a)、图16(d)可知,虽然两者面临的修复环境不同,但是整体韧性均随着修复时间的增加相应增加,时间与韧性成指数关系,两者的优化状态不能同时出现,符合Pareto最优解的特性;不同的是,在考虑综合韧性指标系数相同而修复时期系数变化的修复环境下图16(d),韧性指标在修复第18个月以前迅速增加,而在18个月以后缓慢达到峰值状态,表明此种修复环境对时间的反应明显更加敏感。对比图16(b)、图16(e)可知,无论在何种修复环境下碎片恢复性与时间的关系都相对较弱;但既有的结果仍然表明,在修复时期调整系数不变而综合韧性指标调整系数变化的情况下图16(b)得到的优化结果中两者呈正比例关系,当且仅当两者均衡时其性能达到最佳。对比图16(c)、图16(f)可知,无论处于何种修复环境之下,两者的关系总是一方随着另一方的增加而减少的负相关状态,如图16(f)所示,当综合韧性分别处于0.6、0.7、0.85时,其对应的碎片恢复性仅为0.4、0.45、0.46;不同之处在于,在综合韧性指标调整系数不变而修复时期调整系数变化的修复环境下图16(f)碎片化恢复性与韧性对应的修复结果层次更加分明,表明此环境下两者的优化结果提升程度更加明显。
3.2.4 碎片化的影响
在以上两阶段的修复中可以发现碎片化理论在各优化阶段中都具有一定的适应性,但是其对分阶段优化过程的影响不尽相同,通过对各修复阶段动态调整分析碎片化的影响规律。
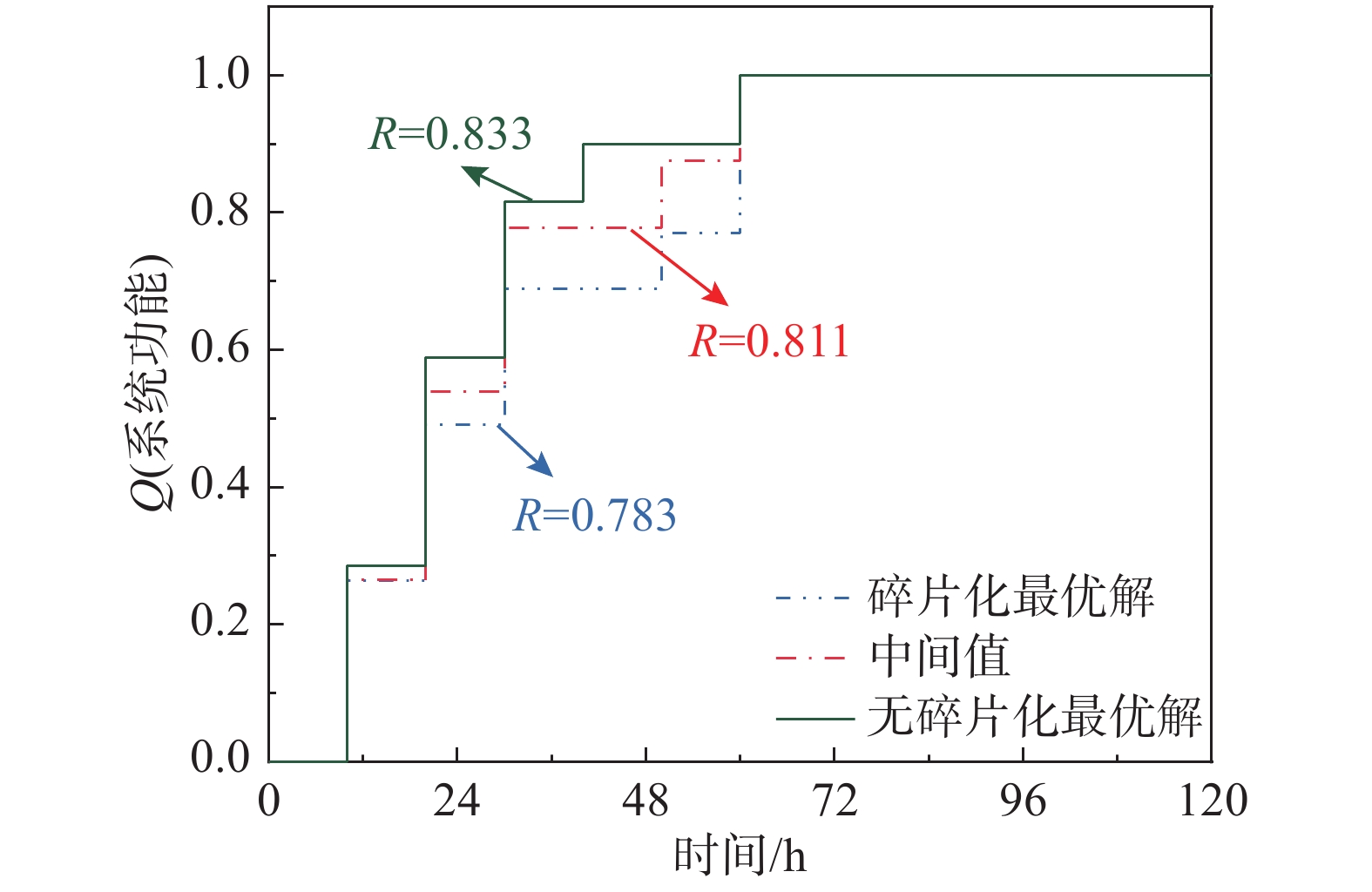
如图17所示为有无碎片化理论参与的最优解系统功能变化,在考虑碎片化的优化结果中系统韧性0.783最小,而采用相应修复次序的不考虑碎片化的结果0.811次之,不经碎片化理论仅考虑连通性的最优结果韧性达到最大0.833,显然碎片化理论在一定程度上降低了优化结果的韧性水平,下降程度约为6%。
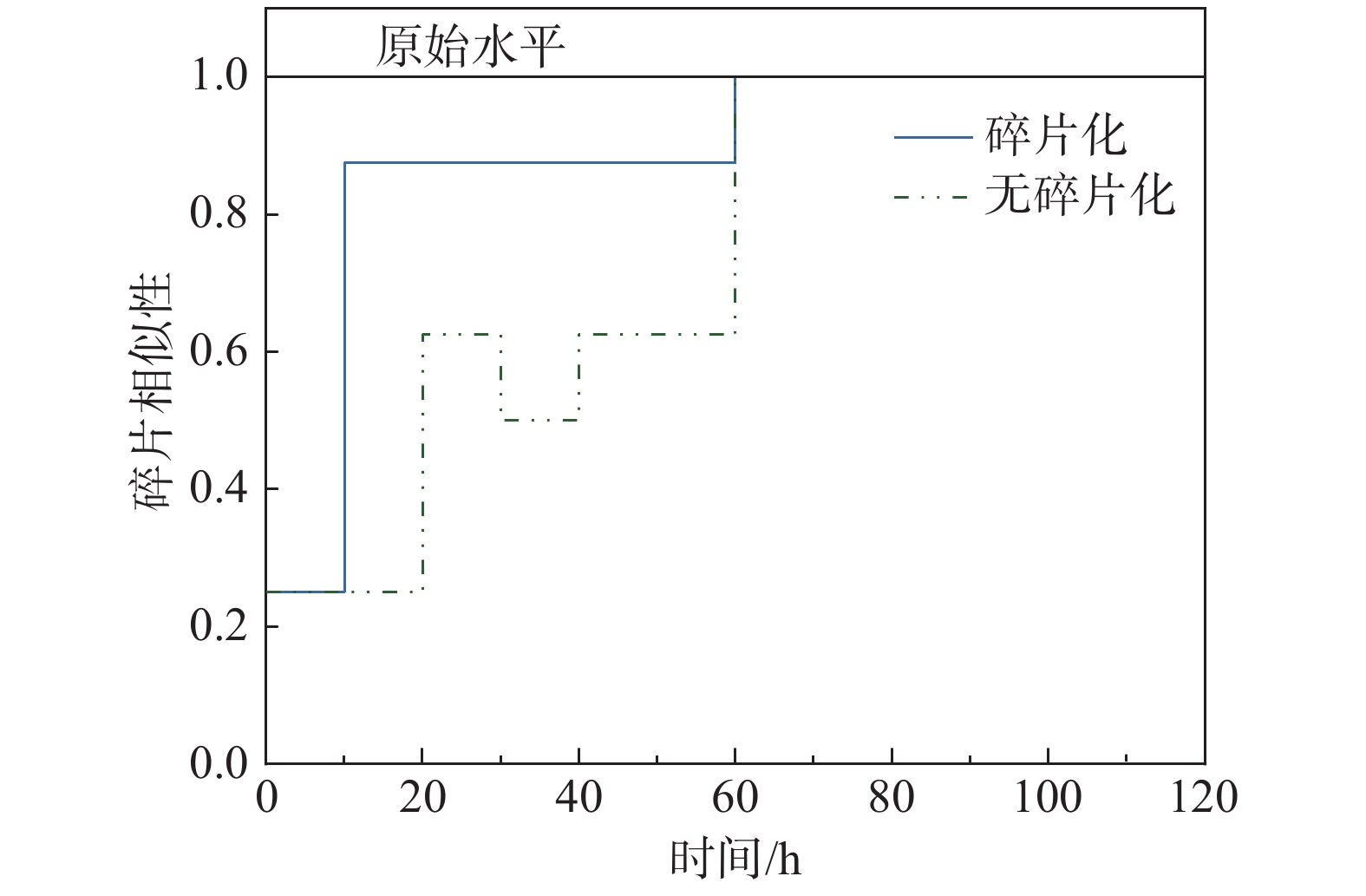
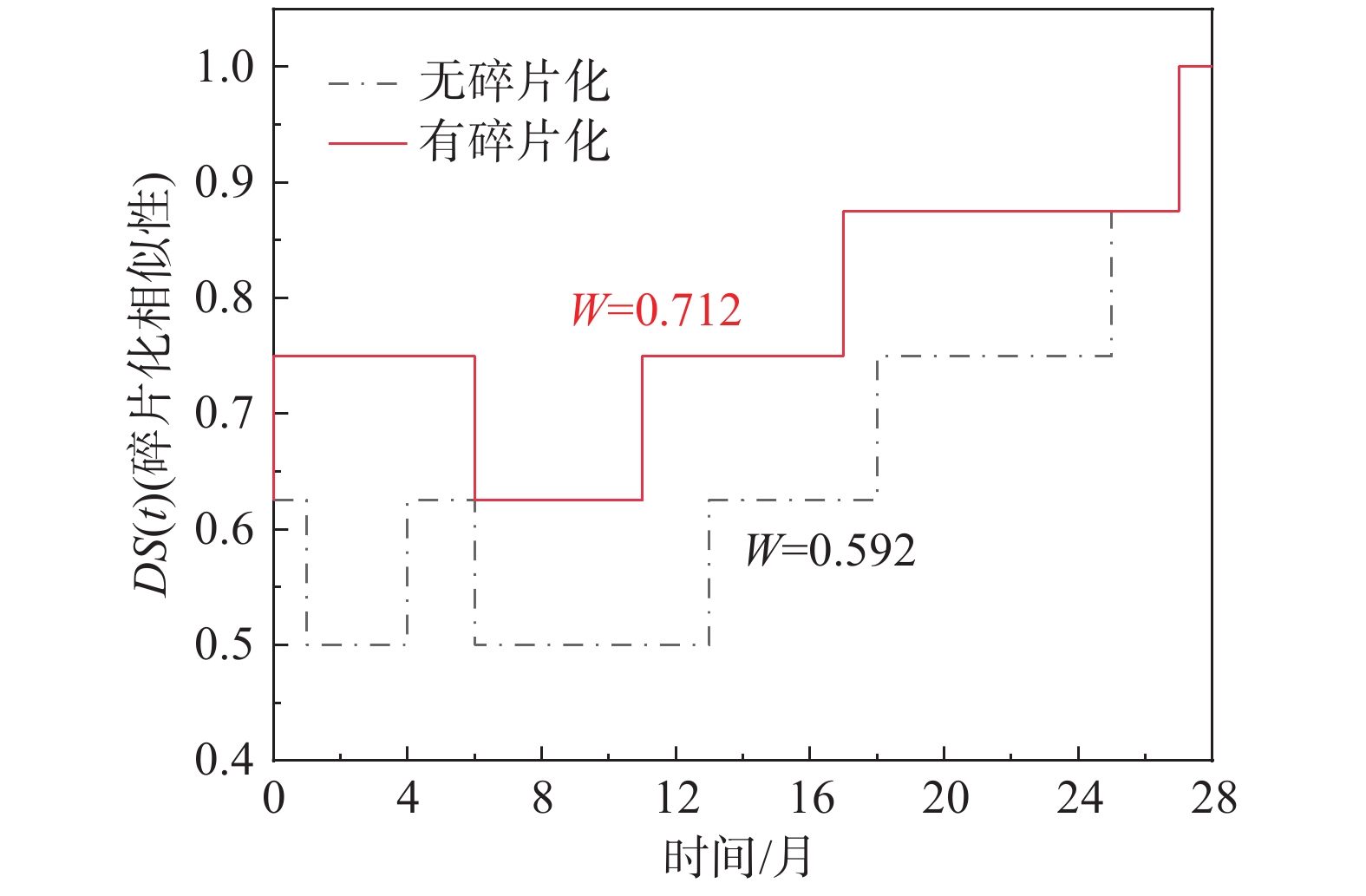
如图18所示,采用了碎片化理论的最优修复结果虽然降低了系统整体功能水平,但是相对于不考虑碎片理论的结果却提升了修复过程中与路网原始通行水平的相似性,从交通密度层面保留了一定的震前通行能力。由于震后修复阶段的碎片化理论作为单独的优化指标存在,故分别针对有无碎片化理论的框架进行优化计算,取两者共有的时间-韧性关系进行对比如图19。
如图19展示了有无碎片化理论参与下韧性与时期调整系数均为1时的优化结果。即使在没有碎片化理论参与的情况下,仅针对韧性及时间的优化依然有效,且与原本的优化结果基本保持一致;但是在碎片化理论的参与的优化中,所得结果充分保留了桥梁网络在修复过程中维持原有通行水平的能力,保证了修复顺序的先进性。
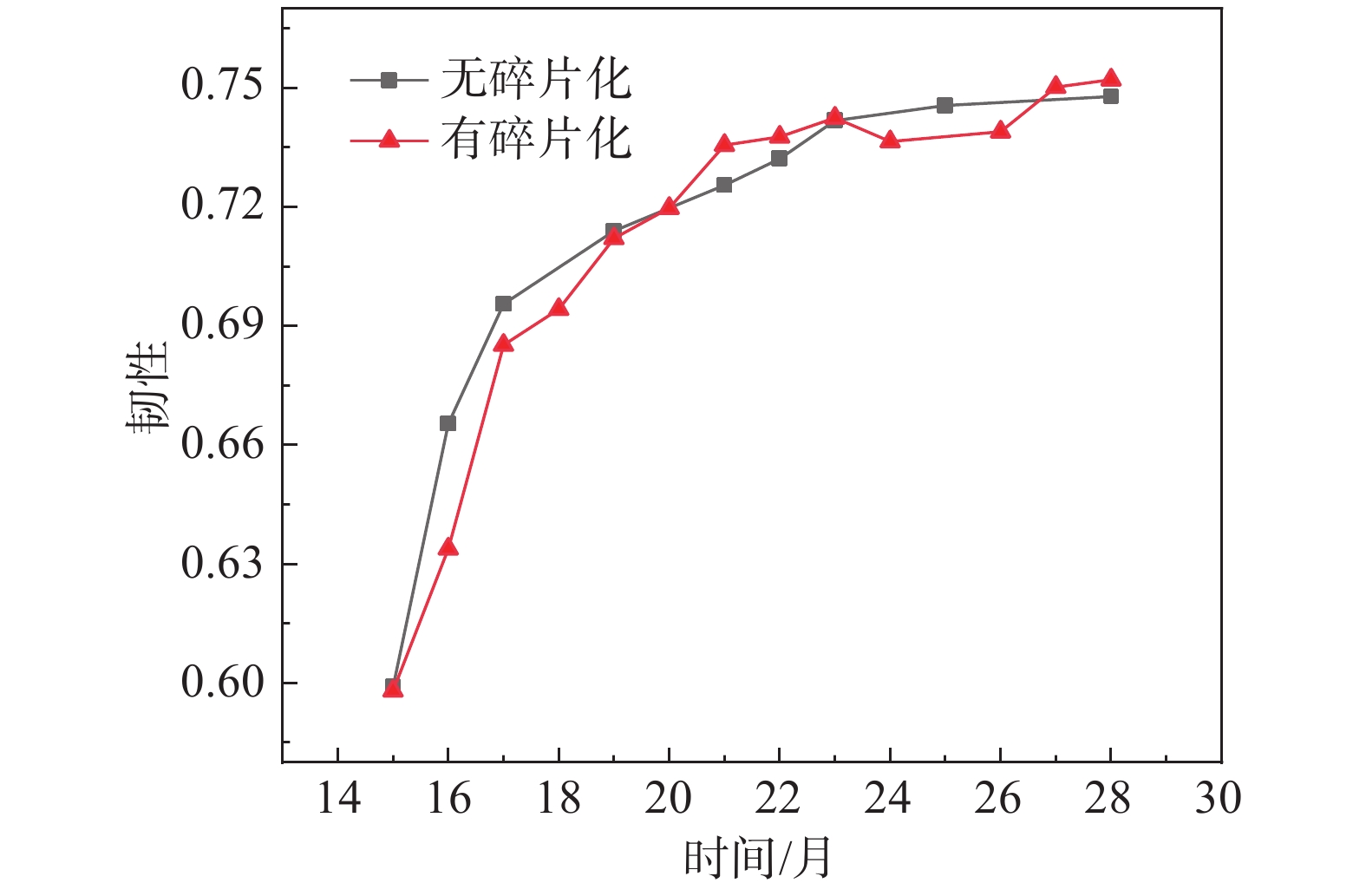
如图20所示,修复时间为28个月时对应的优化结果对比,相比之下碎片化理论得到的结果中碎片化恢复性提升了20.3%,显然在碎片化理论参与的优化中得到的优化结果优势明显。
4 结论
本文针对城市桥梁网络的震后修复需要,在已有决策框架的基础上做出调整,引入基于密度的桥梁网络碎片化分区以表征地震造成的损伤状态,提出了考虑连通性以及碎片化相似性的抢险救灾修复;给出考虑经济性、恢复性的双重韧性指标,对震后长期修复阶段分时期处理,并通过遗传算法进行修复顺序优化。主要结论如下:
(1)给出的桥梁网络碎片化分区理论可以有效刻画整体网络的地震受损状态;为基于此理论的两个修复阶段提供了合理依据,抢险救灾阶段韧性提升程度达到52.3%且震后修复阶段形成了三维优化。
(2)定义的成本韧性指标反映出修复过程中的成本利用状况,恢复韧性指标反映出网络性能状况;区别于传统韧性指标的单一化方向,该指标更具有多样性,且两者相结合的综合韧性指标可以根据决策者的需求自由调整,具备很好的灵活性。
(3)针对震后修复各时期的不同需求,基于已有框架更新的震后两修复阶段同样可以很好地应用于震后桥梁网络修复顺序优化问题,且对于不同修复环境下的修复计划都具有相当的适应性,震后修复时期的阶跃处理也增加了其适用范围,强调初期修复({{{\sigma _{\rm{s}}}} \mathord{\left/ {\vphantom {{{\sigma _{\rm{s}}}} {{\sigma _{\rm{f}}}}}} \right. } {{\sigma _{\rm{f}}}}}=4)的综合韧性阈值达到0.77。
(4)考虑碎片化理论的优化过程所得结果综合考虑到了时间、韧性、碎片化三个方面的近似最优解,且补充了桥梁网络基于通行密度的修复度量以及在不同维度的修复,使桥梁网络碎片化分区在应急阶段提高了其对于原始水平的相似性,在修复阶段使其碎片化恢复性提升20.3%。
(5)在对城市桥梁网络震后两阶段的修复优化级的算例分析中,基于碎片化分区的震后优化方法对震后桥梁修复顺序在应急或是修复阶段都有良好的表现,对桥梁网络震后优先级的分析比较适用。
需要指出的是:对于桥梁网络的碎片化分区仅考虑了其基于密度的划分方式,这弱化了地震对整体网络的影响,实际的震害影响往往更加复杂;今后工作将分别考虑碎片化分区理论的地震影响因素以及其在修复模型中的深层次应用。
-
表 1 节点间距离
Table 1 Distance between node
节点 节点 局部密度 A B C D E F G H I J K L A − 0.89 − 0.89 − 0.10 − 0.95 − − − − 1 B 0.89 − 0.30 − 0.64 − 0.10 − − − − − 2 C − − − − − − − − 2 D − − − − − − − − 2 E − − − − 0.81 0.10 − 0.00 − 2 F 0.10 − 0.81 − 0.59 − − − 0.89 − 0.10 2 G − 0.10 − 0.10 − 0.89 − 0.30 − − − − 3 H 0.95 − 0.59 − 0.81 − 0.30 − − − − − 1 I − − − − 0.10 − − − − 0.10 − 0.59 2 J − − − − − 0.89 − − 0.10 − 0.30 − 2 K − − − − 0.00 − − − − 0.30 − 0.30 3 注:加粗部分表示该节点间距离小于其距离阈值。 表 2 桥梁震后能力损伤
Table 2 Capacity damage of bridge after earthquake
损伤等级 通行能力损失率\xi 未破坏(N) 0.00 轻微破坏(L) 0.00 中度破坏(M) 0.25 严重破坏(E) 0.50 基本倒塌(C) 1.00 表 3 桥梁网络基本参数
Table 3 Basic parameters of bridge network
路段 节点 道路参数 地震参数 桥梁 桥梁参数 路长/km 均交通量(pcu/h) 基本通行能力(pcu/h) 类型 新建费用(百万元) 损伤程度 抢险时间/h 修复
时间/月通行能力损失率ξ 1 (1,2) 0.60 1226 1550 地震断裂带震中位置距路网较近,地震动为浅源地震,震源深度10 km 1 MSSS steel 20.38 E 10 4 0.50 2 (2,3) 0.60 1344 2340 2 MSSS steel 22.75 L − 1 0.00 3 (1,8) 0.60 857 1000 3 MSSS steel 23.45 E 10 3 0.50 4 (1,5) 0.70 984 490 4 MSSS steel 18.50 M − 2 0.25 5 (2,4) 1.00 1923 2340 5 MSSS steel 19.42 C 10 5 1.00 6 (3,4) 0.85 1264 1700 6 MSSS con 25.34 M − 2 0.25 7 (7,8) 0.85 1123 300 7 MSC steel 15.22 N − − 0.00 8 (6,7) 0.80 610 830 8 MSC steel 15.39 E 10 1 0.50 9 (4,5) 0.85 418 470 9 MSC steel 20.54 E 10 4 0.50 10 (8,9) 0.85 556 780 10 MSC steel 21.47 M − 2 0.25 11 (7,10) 0.80 398 500 11 MSC steel 30.05 C 10 5 1.00 12 (6,10) 0.60 536 350 12 MSC con 41.66 E 10 3 0.50 13 (6,11) 0.60 941 1100 13 MSC con 22.56 M − 2 0.25 14 (5,11) 0.60 1231 2340 14 MSC con 30.40 E 10 4 0.50 15 (5,12) 0.70 547 400 15 MSSS con 35.79 E 20 3 0.50 16 (9,10) 0.80 1238 2590 16 MSSS con 20.58 E 10 3 0.50 17 (11,12) 0.85 1024 1550 17 MSSS con 34.22 L − 1 0.00 注:MSSS steel为多跨简支钢梁桥;MSC steel为多跨连续钢梁桥;MSSS con为多跨简支混凝土梁桥;MSC con为多跨连续混凝土梁桥。 表 4 碎片化分区对比
Table 4 Comparison of fragmented partitions
震前 抢险救灾前 震后修复前 [3, 7] [1] [3, 7, 10] [1, 2, 5, 6, 9] [3, 7] [2, 6] [8] [2, 4, 5, 6, 9, 13, 14, 15, 17] [8] [10] [8, 10, 11, 12, 16] [11] [11] − [12] [12] − [1, 4, 5, 9, 13, 14, 15, 17] [4, 13, 14, 15] − [16] [16] − − 注:加粗部分为每个碎片的密度峰值节点DPN。 -
[1] BRUNEAU M, CHANG S E, EGUCHI R T, et al. A Framework to quantitatively assess and enhance the seismic resilience of communities [J]. Earthquake Spectra, 2003, 19(4): 733 − 752. doi: 10.1193/1.1623497
[2] ZOBEL C W, KHANSA L. Characterizing multi-event disaster resilience [J]. Computers & Operations Research, 2014, 42: 83 − 94.
[3] HENRY D, RAMIREZ-MARQUEZ J E. Generic metrics and quantitative approaches for system resilience as a function of time [J]. Reliability Engineering & System Safety, 2012, 99: 114 − 122.
[4] CHEN L C, MILLER-HOOKS E. Resilience: An indicator of recovery capability in intermodal freight transport [J]. Transportation Science, 2012, 46(1): 109 − 123. doi: 10.1287/trsc.1110.0376
[5] BOCCHINI P, FRANGOPOL D M. Optimal resilience- and cost-based postdisaster intervention prioritization for bridges along a highway segment [J]. Journal of Bridge Engineering, 2012, 17(1): 117 − 129. doi: 10.1061/(ASCE)BE.1943-5592.0000201
[6] KARAMLOU A, BOCCHINI P. Sequencing algorithm with multiple-input genetic operators: Application to disaster resilience [J]. Engineering Structures, 2016, 117: 591 − 602. doi: 10.1016/j.engstruct.2016.03.038
[7] EDRISSI A, NOURINEJAD M, ROORDA M J. Transportation network reliability in emergency response [J]. Transportation Research Part E: Logistics and Transportation Review, 2015, 80: 56 − 73. doi: 10.1016/j.tre.2015.05.005
[8] 刘振亮. 考虑震后救援能力的城市桥梁网络抗震性能评估研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. LIU Zhenliang. Seismic performance assessment of Urban bridge network considering the post-disaster evacuation capacity [D]. Harbin: Harbin Institute of Technology, 2015. (in Chinese)
[9] ZHANG W L, WANG N Y, NICHOLSON C. Resilience-based post-disaster recovery strategies for road-bridge networks [J]. Structure and Infrastructure Engineering, 2017, 13(11): 1404 − 1413. doi: 10.1080/15732479.2016.1271813
[10] ANWAR T, LIU C F, VU H L, et al. Partitioning road networks using density peak graphs: Efficiency vs. accuracy [J]. Information Systems, 2017, 64: 22 − 40. doi: 10.1016/j.is.2016.09.006
[11] 侯本伟, 李小军, 韩强, 等. 基于多指标分析的路网单元抗震改造重要度评价[J]. 中国科学: 技术科学, 2018, 48(2): 217 − 228. doi: 10.1360/N092017-00040 HOU Benwei, LI Xiaojun, HAN Qiang, et al. Seismic retrofit priority assessment of highway networks based on multi-indices analysis [J]. Scientia Sinica Technologica, 2018, 48(2): 217 − 228. (in Chinese) doi: 10.1360/N092017-00040
[12] ZOU Q L, CHEN S R. Enhancing resilience of interdependent traffic-electric power system [J]. Reliability Engineering & System Safety, 2019, 191: 106557.
[13] KAVIANI A, THOMPSON R G, RAJABIFARD A, et al. A model for multi-class road network recovery scheduling of regional road networks [J]. Transportation, 2020, 47(1): 109 − 143. doi: 10.1007/s11116-017-9852-5
[14] 吕彪, 高自强, 管心怡, 等. 基于日变交通配流的城市道路网络韧性评估[J]. 西南交通大学学报, 2020, 55(6): 1181 − 1190. doi: 10.3969/j.issn.0258-2724.20191214 LYU Biao, GAO Ziqiang, GUAN Xinyi, et al. Resilience assessment of urban road network based on day-to-day traffic assignment [J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1181 − 1190. (in Chinese) doi: 10.3969/j.issn.0258-2724.20191214
[15] LIU K Z, ZHAI C H, DONG Y. Optimal restoration schedules of transportation network considering resilience [J]. Structure and Infrastructure Engineering, 2021, 17(8): 1141 − 1154. doi: 10.1080/15732479.2020.1801764
[16] 寇峥, 李宁. 基于NSGA-Ⅱ的城市桥梁系统震后可恢复性分析与优化[J]. 工程力学, 2021, 38(3): 148 − 158, 180. doi: 10.6052/j.issn.1000-4750.2020.05.0290 KOU Zheng, LI Ning. Study on earthquake resilience analysis and optimization for urban bridge network system Based on NSGA-II algorithm [J]. Engineering Mechanics, 2021, 38(3): 148 − 158, 180. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.0290
[17] 宗成才, 冀昆, 温瑞智, 等. 城市燃气管网三维度抗震韧性定量评估方法[J]. 工程力学, 2021, 38(2): 146 − 156. doi: 10.6052/j.issn.1000-4750.2020.04.0219 ZONG Chengcai, JI Kun, WEN Ruizhi, et al. Three-dimensional seismic resilience quantification framework for the urban gas network [J]. Engineering Mechanics, 2021, 38(2): 146 − 156. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.04.0219
[18] 张望欣, 韩强, 温佳年, 等. 基于地震灾害管理的桥梁网络韧性决策框架[J]. 土木工程学报, 2023, 56(4): 72 − 82. doi: 10.15951/j.tmgcxb.21121231 ZHANG Wangxin, HAN Qiang, WEN Jianian, et al. A decision framework for bridge networks resilience based on earthquake disaster management [J]. China Civil Engineering Journal, 2023, 56(4): 72 − 82. (in Chinese) doi: 10.15951/j.tmgcxb.21121231
[19] ZHANG M Y, YANG X J, ZHANG J, et al. Post-earthquake resilience optimization of a rural “road-bridge” transportation network system [J]. Reliability Engineering & System Safety, 2022, 225: 108570.
[20] LIU Z L, LI S C, GUO A X, et al. Comprehensive functional resilience assessment methodology for bridge networks using data-driven fragility models [J]. Soil Dynamics and Earthquake Engineering, 2022, 159: 107326. doi: 10.1016/j.soildyn.2022.107326
[21] SHARMA N, TABANDEH A, GARDONI P. Regional resilience analysis: A multiscale approach to optimize the resilience of interdependent infrastructure [J]. Computer-Aided Civil and Infrastructure Engineering, 2020, 35(12): 1315 − 1330. doi: 10.1111/mice.12606
[22] 缪惠全, 钟紫蓝, 侯本伟, 等. 基于系统动力学的城市供水管网动态抗震韧性评估方法[J]. 工程力学, 2023, 40(12): 99 − 112. doi: 10.6052/j.issn.1000-4750.2022.02.0154 MIAO Huiquan, ZHONG Zilan, HOU Benwei, et al. Dynamic seismic resilience assessment method for water distribution networks based on system dynamics [J]. Engineering Mechanics, 2023, 40(12): 99 − 112. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.02.0154
[23] WANG D, ZHAO X Y, LIU Y. Effect of spatial variation of earthquake ground motions on seismic vulnerability of urban road network considering building environment [J]. Buildings, 2022, 12(3): 12030308. doi: 10.3390/buildings12030308
[24] 牟健慧, 段培永, 高亮, 等. 基于混合遗传算法求解分布式流水车间逆调度问题[J]. 机械工程学报, 2022, 58(6): 295 − 308. MU Jianhui, DUAN Peiyong, GAO Liang, et al. Hybrid genetic algorithm for distributed flow shop inverse scheduling problem [J]. Journal of Mechanical Engineering, 2022, 58(6): 295 − 308. (in Chinese)
[25] MYEONG S, JUNG Y, LEE E. A study on determinant factors in smart city development: An analytic hierarchy process analysis [J]. Sustainability, 2018, 10(8): 10082606. doi: 10.3390/su10082606
[26] CHANG S E, SHINOZUKA M, MOORE J E. Probabilistic earthquake scenarios: Extending risk analysis methodologies to spatially distributed systems [J]. Earthquake Spectra, 2000, 16(3): 557 − 572. doi: 10.1193/1.1586127
[27] CHANG S E, NOJIMA N. Measuring post-disaster transportation system performance: The 1995 Kobe earthquake in comparative perspective [J]. Transportation Research Part A:Policy and practice, 2001, 35(6): 475 − 494. doi: 10.1016/S0965-8564(00)00003-3
[28] NIELSON B G, DESROCHES R. Analytical seismic fragility curves for typical bridges in the central and southeastern United States [J]. Earthquake Spectra, 2007, 23(3): 615 − 633. doi: 10.1193/1.2756815
-
期刊类型引用(1)
1. 《中国公路学报》编辑部. 中国桥梁工程学术研究综述·2024. 中国公路学报. 2024(12)  百度学术
百度学术
其他类型引用(0)



 下载:
下载: