圆不锈钢管超高性能混凝土短柱轴压性能研究

唐红元; 曾跃佳; 刘烨

doi:10.6052/j.issn.1000-4750.2022.11.0923

圆不锈钢管超高性能混凝土短柱轴压性能研究

唐红元^1,,
曾跃佳^1,,
刘烨^2, ,

1.
西华大学结构工程研究所，成都 610039
2.
四川大学建筑与环境学院深地科学与工程教育部重点实验室，成都 610065

基金项目: 国家自然科学基金项目(52208496)

详细信息

作者简介:
唐红元(1974−)，男，湖北人，教授，博士，主要从事钢结构及组合结构研究(E-mail: tanghyseu@163.com)

曾跃佳(1997−)，女，四川人，硕士生，主要从事钢结构及组合结构研究(E-mail: 1457959839@qq.com)

通讯作者:
刘　烨(1992−)，男，江苏人，副研究员，博士，主要从事装配式结构抗震和组合结构研究(E-mail: liu.ye@scu.edu.cn)

中图分类号: TU398+.9
计量
- 文章访问数: 187
- HTML全文浏览量: 40
- PDF下载量: 50
出版历程
- 收稿日期: 2022-10-31
- 修回日期: 2023-01-10
- 网络出版日期: 2023-04-19
- 刊出日期: 2025-02-24

STUDY ON AXIAL-COMPRESSION PERFORMANCE OF CIRCULAR ULTRA-HIGH PERFORMANCE CONCRETE -FILLED SATAINLESS STELL TUBE COLUMN

1.
Institute of Structural Engineering, Xihua University, Chengdu 610039, China
2.
Key Laboratory of Deep Underground Science and Engineering (Ministry of Education), College of Architecture and Environment, Sichuan University, Chengdu 610065, China

摘要

摘要:
该文对6根超高性能混凝土填充不锈钢管(UHPC-filled circular stainless steel tubular, UFCSST)短柱、3根普通混凝土填充不锈钢管(Concrete-filled stainless steel tubular columns, CFSST)短柱以及3根不锈钢管进行轴压试验，试件参数包括不锈钢管壁厚和核心混凝土强度等级。观察了试件的受力破坏过程及形态，获取了荷载-位移曲线，通过试件受力过程的破坏形态、荷载-位移曲线、荷载-应变曲线、混凝土贡献率和强度提高系数对UFCSST轴压力学性能进行了分析。结果表明：UFCSST短柱失效模型与套箍系数相关，当套箍系数大于1.03时，核心混凝土由剪切型破坏向横向膨胀转变。荷载-位移曲线在峰值荷载后的变化趋势依据套箍系数大小可分为三类：一是存在下降段，后再缓慢回升至峰值荷载；二是平稳发展；三是缓慢上升。不锈钢管厚度一定时，UHPC等级对承载力影响较小，最大能提升承载力14.8%。由于UHPC强度高且内部含有钢纤维减缓UHPC内部裂缝和变形的发展，导致UHPC的混凝土贡献率比普通混凝土贡献率高81.6%，而由于UHPC自收缩性和混凝土多轴力学特性，UHPC的强度提高系数比普通混凝土低46.4%。国外部分规范计算结果较试验结果偏于保守，最大偏差可达22.4%，而国内CECS 28: 2012的计算结果较试验承载力高出10.4%。基于统一强度理论提出了UFCSST承载力理论计算模型。
- 承载力 /
- 轴压试验 /
- 超高性能混凝土 /
- 不锈钢管 /
- 预测模型
Abstract:
In this paper, 6 short columns of ultra-high performance concrete filled stainless steel tubes (UFCSST), 3 short columns of ordinary concrete filled stainless steel tubes (CFSST), and 3 stainless steel tubes are tested under axial compression. The test parameters were stainless steel tube wall thickness and core concrete strength. The failure process and morphology of the specimen was observed, and the load-displacement curves were obtained. The axial-compressive properties of UFCSST were analyzed through the failure morphology, load-displacement curve, load-strain curve, concrete contribution rate and strength improvement coefficient of the specimen. The results show that the failure model of UFCSST short columns is related to the confinement coefficient. When the confinement coefficient is greater than 1.03, the core concrete changes from shear failure to lateral expansion. The change trend of load-displacement curve after the peak load can be divided into three categories according to the value of confinement coefficient: an initial descending section followed by slow increase to the peak load, stable development, and slow increase. When the thickness of stainless steel tube is fixed, the UHPC grade has little influence on the bearing capacity, and the maximum bearing capacity can be increased by 14.8%. The high strength of UHPC and the inclusion of steel fibers inside would slow down the development of cracks and inside deformation, causing the concrete contribution rate of UHPC 81.6% higher than that of ordinary concrete; however, due to the autogenous shrinkage of UHPC and the multiaxial mechanical properties of concrete, the strength improvement coefficient of UHPC is 46.4% lower than that of ordinary concrete. The calculation results of some foreign codes are more conservative than the test results, with the maximum deviation of 22.4%, while the calculation results of CECS 28: 2012 in China are 10.4% higher than the test bearing capacity. Based on the unified strength theory, a theoretical calculation model of UFCSST bearing capacity is proposed.
- bearing capacity /
- axial compression test /
- ultra-high performance concrete /
- stainless steel /
- prediction model

HTML全文

普通碳钢管混凝土柱(Concrete-filled steel tubular columns, CFST)易腐蚀，特别是在海洋环境中服役时，维护成本较高^[1]。与碳钢相比，不锈钢具有良好的延展性和耐腐蚀性，降低了维护成本，采用不锈钢替代传统碳钢引起广泛关注。目前对普通混凝土填充不锈钢开展的研究较多，已有文献[2-7]表明：现有规范对混凝土填充不锈钢管柱(Concrete-filled stainless steel tubular columns, CFSST)的预测相对保守；不同混凝土等级^[8]与不同径厚比^[9]的不锈钢管对CFSST承载力性能影响不同。

与普通混凝土相比，高强混凝土在峰值后，延性较低，呈陡坡下降^[10]，脆性越来越明显^[11]。通过添加钢纤维可以提高混凝土的韧性与钢管混凝土的耗能能力^[12]。近年来混凝土技术的发展与硅灰、高效减水剂的工程应用，制作抗压强度大于120 MPa的超高性能混凝土(Ultra-high performance concrete, UHPC)逐渐受到关注。UHPC受荷载作用，应力区会出现许多裂缝，但由于钢纤维的“桥接”作用使得构件不会迅速整体断裂，UHPC破坏时内部钢纤维拔出或断裂^[13-14]，产生高能量耗散，导致脆性破坏^[15]。为了充分利用UHPC材料的特性，需要提供更强的侧向约束来改善其延性，防止其提早开裂。不锈钢具有较大屈服强度和屈服应变，二者形成的UFCSST能有效克服UHPC的脆性。而UFCSST具有自重较轻，耐腐蚀的特点，适用于对耐久性和对构件承载力要求较高的高层和沿海建筑^[16]，不仅节省建筑空间，同时还减少建筑材料的使用^[17]，有较好的工程应用前景。钢管混凝土中核心混凝土在承载过程中始终处于较高的围压。WANG等^[18]通过不同围压下UHPC的力学响应，发现围压增大对UHPC柱的承载力和延性均有所提升。

目前，超高性能混凝土填充碳钢管(UHPC-filled steel tubular, UFST)的研究已较为成熟。GULER等^[19]对比了不同壁厚碳钢管对超高性能混凝土的约束作用，结果表明：碳钢管壁厚增加能明显增大钢管混凝土柱的延性，且目前规范对超高性能混凝土填充碳钢管的承载力预测偏差较大；CHEN等^[20]通过参数分析，发现圆钢管能提供UHPC较好的约束，但UHPC组合柱的强度与延性提高程度不如普通混凝土组合柱的显著；XU等^[21]讨论了钢管壁厚和混杂纤维特征参数对UFST试件刚度、极限荷载、破坏模式和峰值后行为的影响。国内外许多学者对UFST的轴压、抗弯等力学性能取得了诸多研究成果，对提升UHPC力学性能特也提出了诸多有效措施，但是对于海洋大气等恶劣环境下服役的试件，碳钢管表面的锈蚀易造成应力集中导致试件承载能力下降^[22-23]。使用抗腐蚀性、耐久性较好的不锈钢代替普通碳钢是解决这一问题的方法之一。并且，碳钢与不锈钢力学性能存在显著差异，普通混凝土与超高性能混凝土基本力学性能也存在明显不同，因此，UHPC填充不锈钢管的基本力学性能还有待进一步研究。

当前对超高性能混凝土填充不锈钢管(UHPC filled stainless steel tubular, UFSST)柱力学性能的研究鲜见，由于试验数据缺少，相关规范对UFSST的适用性尚未明确。为促进UFSST在复杂服役环境如海洋平台、沿海建筑、桥梁以及对耐久性要求较高的重要建筑中的工程应用实践，开展UFSST轴压性能的研究非常必要。根据以往试验结果^{[9, 20, 24]}，圆形钢管对混凝土约束较好。基于此，本文对圆双相不锈钢管超高性能混凝土短柱(UHPC filled circular stainless steel tubular, UFCSST)进行了轴压试验，分析了套箍系数对破坏模式、荷载-位移曲线、混凝土贡献率和强度提高系数的影响，并将试验结果与相关规范进行了比较，提出适用于UFCSST的承载力预测公式。

1 试验方案

1.1 试件设计与制作

试验共设计12根试件，包括6个UFCSST试件、3个CFSST试件、3个圆不锈钢管试件。试样的长径比(L/D)控制在3左右。试件参数如表1所示，其中双相不锈钢管名义外径和长度为114 mm和342 mm，钢管名义壁厚包括4 mm、6 mm和8 mm三种，混凝土等级包括普通C40混凝土、UHPC-120和UHPC-150。试件编号中第一个字母C表示试件为圆截面，第二个数字表示混凝土等级，第三个数字表示不锈钢管名义厚度。

表 1 试件的详细参数

Table 1. Detailed parameters of the specimen

试件编号	D/mm	L/mm	t/mm	f_c/MPa	f_0.2/MPa
C-0-4	114.5	342.1	4.2	−	558.7
C-0-6	112.3	341.5	6.2	−	641.0
C-0-8	114.3	341.9	9.2	−	546.7
C-40-4	114.3	342.5	4.0	36.7	558.7
C-40-6	113.5	342.0	6.3	36.7	641.0
C-40-8	114.2	342.0	9.2	36.7	546.7
C-120-4	114.4	342.5	4.4	119.4	558.7
C-120-6	114.1	342.2	6.5	119.4	641.0
C-120-8	114.4	341.9	9.2	119.4	546.7
C-150-4	114.8	342.5	4.1	144.9	558.7
C-150-6	114.0	341.9	6.5	144.9	641.0
C-150-8	114.3	342.5	9.1	144.9	546.7
注：D为试件的实测外径；L为柱的实测高度；t为不锈钢管实测壁厚；f_c为圆柱体抗压强度；f_0.2为不锈钢名义屈服应力。

下载: 导出CSV

| 显示表格

试件制作过程如下：1)将不锈钢管切割至设计高度，打磨并清洗不锈钢管与塑料模具内污渍；2)分两次均匀浇入核心混凝土，减少空腔出现，同时浇筑立方体试块；3)置于振动台振捣1 min，浇筑完毕后，将试件置于实验室内24 h；4)室温养护28 d，养护结束后，打磨端部多余核心混凝土至与钢管端面平齐，完成试件制备。

1.2 材料性能

UHPC配合比见表2，钢纤维参数见表3。UHPC-120、UHPC-150依据《活性粉末混凝土》(GB/T 31387−2015)^[25]分别制作3个100 mm×100 mm×100 mm立方体试块用于轴心受压试验，3个100 mm×100 mm×300 mm试块用于弹性模量测验。依据《普通混凝土力学性能试验方法标准》(GB/T 50081−2019)^[26]，对C40混凝土制作6个150 mm×150 mm×150 mm立方体混凝土试块，确定立方体抗压强度f_cu，并根据文献[27]转化为圆柱体抗压强度f_c，按《混凝土结构设计规范》(GB 50010−2010)^[28]确定弹性模量E_c。表4为混凝土立方体抗压强度(f_cu)、圆柱体抗压强度(f_c)和弹性模量(E_c)等性能指标的均值。

表 2 UHPC配合比

Table 2. Mix proportions of UHPC /(kg·m⁻³)

成分	胶凝材料	石英砂	水	高性能减水剂	钢纤维
含量	1035.6	1035.6	184.7	13/16	181
注：UHPC-120和UHPC-150采用不同的预混凝料(胶凝材料和石英砂)，配合比中仅高性能减水剂含量不同，分别为13 kg·m⁻³和16 kg·m⁻³。

下载: 导出CSV

| 显示表格

表 3 钢纤维参数表

Table 3. Properties of steel fiber

长度 /mm	直径/mm	长径比	密度/(kg·m⁻³)	极限强度/MPa	弹性模量/GPa
13	0.2	65	7900	2900	200

下载: 导出CSV

| 显示表格

表 4 混凝土材料性能

Table 4. Performance of concrete material

混凝土等级	混凝土立方体抗压强度f_cu/MPa	圆柱体抗压强度f_c/MPa	弹性模量E_c/MPa
C40	44.0	36.7	32 500
UHPC-120	129.2	119.4	44 200
UHPC-150	154.3	144.9	44 800

下载: 导出CSV

| 显示表格

采用2205双相型不锈钢管，根据《金属材料拉伸试验第1部分：室温试验方法》(GB/T 228.1−2010)^[29]对3个标准骨头试样进行钢材单轴拉伸试验。材料性能如图1和表5所示。

图 1 不锈钢拉伸应力-应变试验曲线

Figure 1. Tensile stress-strain experimental curves of steel

下载: 全尺寸图片幻灯片

表 5 钢材力学性能指标

Table 5. Mechanical properties of steel

钢管名义厚度	f_0.2/MPa	f_u/MPa	E₀/GPa
4 mm	558.7	646.0	182.9
6 mm	566.0	728.6	183.6
8 mm	546.7	647.4	183.7
注：E₀为弹性模量；f_0.2为不锈钢名义屈服应力；f_u为极限抗拉强度。表中数值均为平均值。

下载: 导出CSV

| 显示表格

1.3 试验加载方案及测点布置

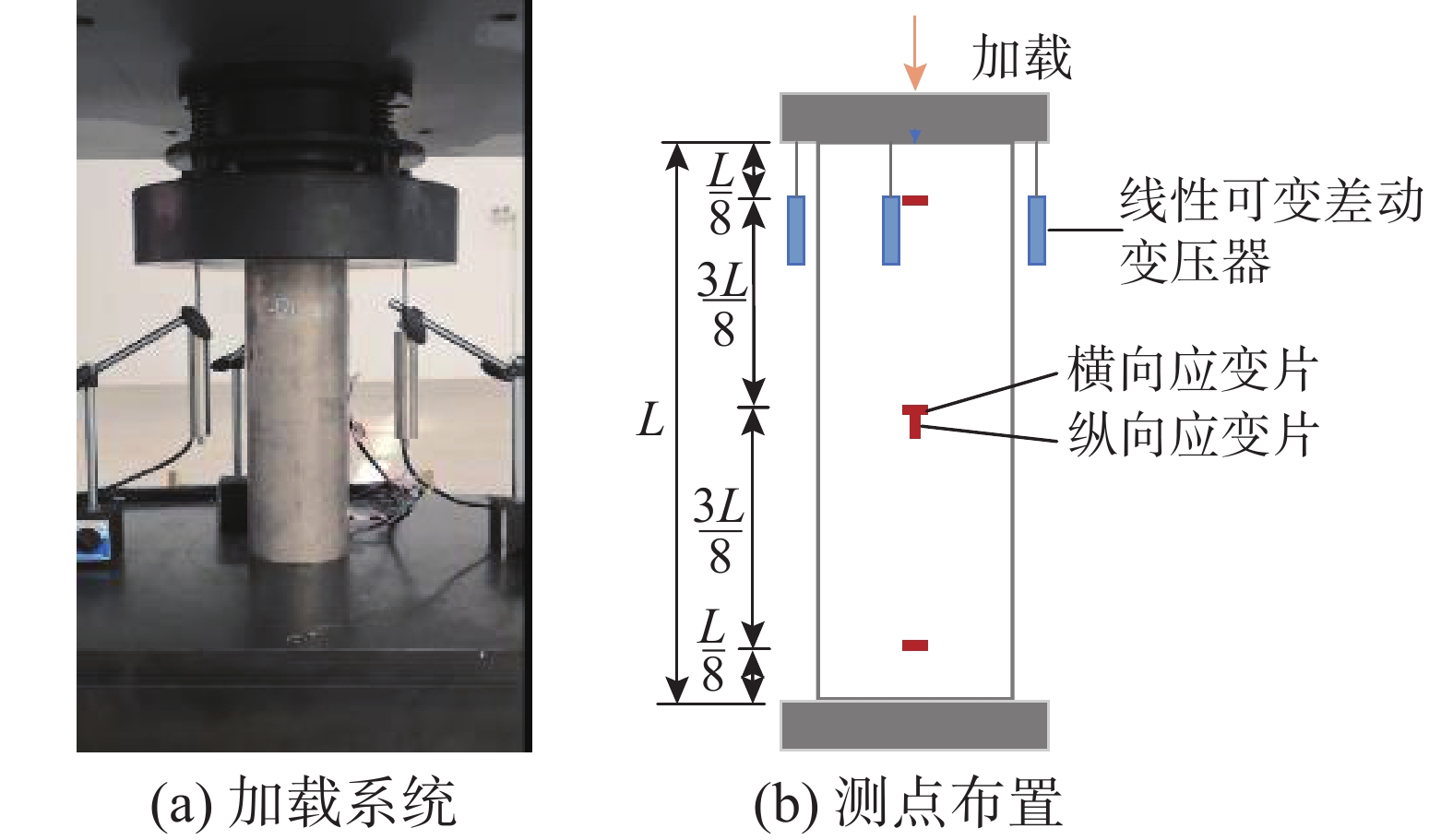
采用5000 kN的液压伺服机进行加载，加载装置如图2所示。在钢管顶部1/8高度、中部1/2高度和底部1/8高度处布置图2(b)所示的应变片，以测量试件横向与轴向应变。柱相邻侧面布置3个线性可变位移传感器(线性可变差动变压器LVDTs)记录试件轴向压缩变形。

图 2 加载系统和测点布置

Figure 2. Loading system and arrangement of measuring points

下载: 全尺寸图片幻灯片

加载前对所有试件进行预加载，以保证试件加载无偏心。预加载时加载速率为0.08 MPa/s，加载至50 kN^[20]。正式加载过程中，采用位移控制加载，加载速率为0.6 mm/min。当试件轴向压缩应变达到0.07^[9]时，试验终止。

2 实验结果与分析

2.1 试验现象与分析

荷载-位移曲线分为四个阶段：I-弹性阶段、II-弹塑性阶段(极限荷载之前)、III-下降段和IV-强化阶段。

试件失效模式如图3，各试件在I、II阶段均无明显变形；临近II阶段末至III阶段末，UFCSST试件持续发出纤维拔出的碎裂声，其外表无明显变形，CFSST试件仍无明显现象；临近IV阶段各试件出现一定程度的变形。同时，试件加载停止时，均在不锈钢管外表面出现环状鼓屈，鼓屈现象随着不锈钢管壁厚的增加愈发不明显。

试件破坏模式总体而言可分为两类：剪切破坏(C-120-4和C-150-4)和横向膨胀(C-150-6和C-120-6)，其余试件无明显破坏现象(C-40-4、C-40-6、C-40-8、C-120-8和C-150-8)。

解剖不锈钢管，如和，发现C-120-4( $\xi$ =0.820)和C-150-4( $\xi$ =0.603)核心混凝土在端部鼓曲部分挤压明显，表面混凝土剥落，混凝土中部出现剪切裂纹，且与端部鼓曲处相连，表现出明显的剪切破坏特征。试件C-120-6( $\xi$ =1.297)和C-150-6( $\xi$ =1.034)中部出现横向膨胀，整体无剪切破坏特征。可以看出，C-40-4( $\xi$ =2.399)端部明显鼓屈，但由于套箍系数较大，不锈钢管提供足够的约束，所以核心混凝土未出现剪切裂纹，中部混凝土表面基本完好。

图 3 试件破坏形态

Figure 3. Specimen failure mode

下载: 全尺寸图片幻灯片

综上可知，不锈钢管受到混凝土轴向压力和径向拉应力产生鼓曲变形，而混凝土状态与套箍系数相关，随着套箍系数增大，混凝土从出现剪切裂纹向横向膨胀转变。

2.2 轴向荷载-位移关系

2.2.1 荷载-位移曲线分类

为试件荷载-位移曲线。根据试验得到的荷载-位移曲线可分为三类，即 $\xi {\leqslant }$ 0.820、1.03 ${\leqslant } \xi {\leqslant }$ 1.30和 $\xi {\geqslant }$ 1.30。

第一类 $\xi {\leqslant }$ 0.820：存在I~IV四个阶段，其中III阶段存在明显下降趋势，IV阶段曲线上升，对应试件C-120-4和C-150-4。从C-120-4和C-150-4荷载-位移曲线在I-弹性阶段，不锈钢管未对混凝土产生约束作用，曲线呈线性增长；随着轴向荷载不断增大，混凝土处于三向受压状态，不锈钢管与混凝土互相变形协调，进入II-弹塑性阶段；曲线斜率逐渐小，达到峰值荷载后进入III-下降段，曲线出现短暂下降，这是由于在C-120-4( $\xi$ =0.820)和C-150-4( $\xi$ =0.603)中，4 mm不锈钢管对UHPC120和UHPC150的约束较弱，达到峰值后UHPC脆性断裂导致承载力下降，过高抗压强度的UHPC与较小壁厚的不锈钢管出现了性能不匹配的情况，不锈钢管提供的侧向约束力不足以使UHPC的性能充分发挥出来，从而出现下降段；随后进入IV-阶段，曲线上升，这是由于不锈钢的应变硬化效应和钢纤维的桥接效应，补偿了UHPC强度退化，以及不锈钢良好的应变硬化效应，荷载下降后又缓慢上升，剩余承载力分别约为峰值荷载的100%与92%。

第二类1.03 ${\leqslant }\xi {\leqslant }$ 1.30：存在I、II和IV阶段，其中III阶段下降不明显或不存在，IV阶段曲线在极限荷载后平稳发展，对应试件C-120-6和C-150-6。如所示，在C-120-6( $\xi$ =1.304)和C-150-6( $\xi$ =1.034)中，不锈钢约束较好，曲线在弹性阶段与弹塑性阶段变化趋势与第一类一致。由于不锈钢管壁厚增大，提供的侧向约束能够有效阻止UHPC脆性断裂，试件发生横向膨胀，达到极限荷载后不存在下降段，强化阶段呈平稳发展状态。

第三类 $\xi {\geqslant }$ 1.30：无III阶段，IV阶段曲线在极限荷载后仍缓慢上升，对应试件C-40-4、C-40-6、C-40-8、C-120-8和C-150-8。此类试件套箍系数较大，减缓不锈钢管的局部变形，不锈钢对UHPC约束较强，因此不存在III阶段；且基于不锈钢较好应变硬化能力，不锈钢管提供的侧向约束力能够使UHPC的性能充分发挥出来，因此IV阶段缓慢上升。曲线在弹性阶段与弹塑性阶段与第一类曲线发展趋势一致，达到峰值荷载后，曲线呈稳定上升状态，套箍系数越大，曲线上升斜率越大。

图 4 UHPCFSST荷载-位移曲线

Figure 4. UHPCFSST load-displacement curve

下载: 全尺寸图片幻灯片

2.2.2 承载力分析

试件极限荷载对比如图5所示。C-40-8比C-40-6和C-40-4承载力提升了93.1%和41.5%；C-120-8比C-120-6和C-120-4承载力分别提升了18.5%和40.7%；C-150-8比C-150-6和C-150-4承载力分别提升了10.8%和49.8%，除C-150-4外(4 mm不锈钢管约束较弱，未能充分发挥UHPC材料特性)，当混凝土等级较高时，不锈钢管厚度对承载力影响较小。

C-150-6比C-120-6承载力提升了14.8%，而C-150-4比C-120-4承载力下降了2.5%，混凝土强度等级提升，承载力反而下降，这是因为混凝土单轴强度越大，4 mm厚的不锈钢管对超高性能混凝土约束相对越弱，剪切破坏发生较早，不锈钢无法阻止剪切裂缝的发生。

图 5 极限荷载对比

Figure 5. Comparison of ultimate load

下载: 全尺寸图片幻灯片

2.3 轴向荷载-应变关系

图6为各试件的荷载N、横向应变ε_t、纵向应变ε_l和不锈钢泊松比ν(ε_t/ε_l)与轴向位移的变化曲线，ε_0.2为不锈钢材屈服应变，空不锈钢管横向应变为ε_t0、纵向应变为ε_l0。试件的轴向应变在极限荷载之前达到屈服应变，环向应变在到达极限荷载附件时达到屈服应变，表明不锈钢已充分发挥。由图6可知，加载初期，试件处于弹性阶段，不锈钢管未对混凝土产生约束作用，荷载-位移曲线线性增长，纵向应变发展速率大于横向应变发展速率；各试件的应变比值与不锈钢泊松比相近，约为钢材单向拉伸时的泊松比。随着轴向荷载不断增加，试件进入弹塑性阶段，此时不锈钢泊松比大于0.3，混凝土处于三向受压状态，受压膨胀，UHPC泊松比逐渐大于不锈钢泊松比，不锈钢管与混凝土相互变形协调，不锈钢管提供侧向约束挤压混凝土，纵向应变首先达到屈服应变，横向应变不断增大，此期间核心混凝土处于弹性状态，导致应力重分布，应变呈非线性增长；应变比值逐渐超过泊松比，不锈钢管的约束作用不断增强。下降段和强化阶段，不锈钢管主要承担横向变形，不锈钢管对混凝土约束越来越强^[30]。

图 6 试件的荷载-应变曲线

Figure 6. Load-strain curves of specimens

下载: 全尺寸图片幻灯片

2.4 试验结果分析

试验结果见。套箍系数 $\xi$ 是影响混凝土与不锈钢管相互作用的主要因素，定义如下^[31]：

$\xi=\frac{f_{0.2} A_{\mathrm{s}}}{f_{\mathrm{c}} A_{\mathrm{c}}}$

(1)

式中：A_s为钢管截面面积；A_c为混凝土截面面积。混凝土贡献率CCR与混凝土强度提高系数CSI定义见2.4.2节。

表 6 试验结果汇总表

Table 6. Test results summary

试样标签	D/t	N_u/kN	$\xi$	CCR	CSI
C-0-4	27.3	942	−	−	−
C-0-6	18.1	1615	−	−	−
C-0-8	12.4	2209	−	−	−
C-40-4	28.6	1212	2.399	1.287	1.095
C-40-6	18.0	1654	4.092	1.024	1.107
C-40-8	12.4	2341	6.272	1.059	1.218
C-120-4	26.0	2201	0.820	2.337	1.157
C-120-6	17.6	2612	1.297	1.542	1.132
C-120-8	12.4	3096	1.923	1.375	1.203
C-150-4	28.0	2146	0.603	2.283	1.038
C-150-6	17.5	2902	1.034	1.796	1.229
C-150-8	12.6	3215	1.564	1.397	1.146
注：N_u为试件实测极限承载力，若荷载-位移曲线无下降段，取纵向应变达到0.01时对应的荷载^[32]；ξ为套箍系数；CCR为混凝土贡献率；CSI为混凝土强度提高系数；D/t为试件的实测外径与不锈钢管实测壁厚之比。

下载: 导出CSV

| 显示表格

2.4.1 混凝土贡献率

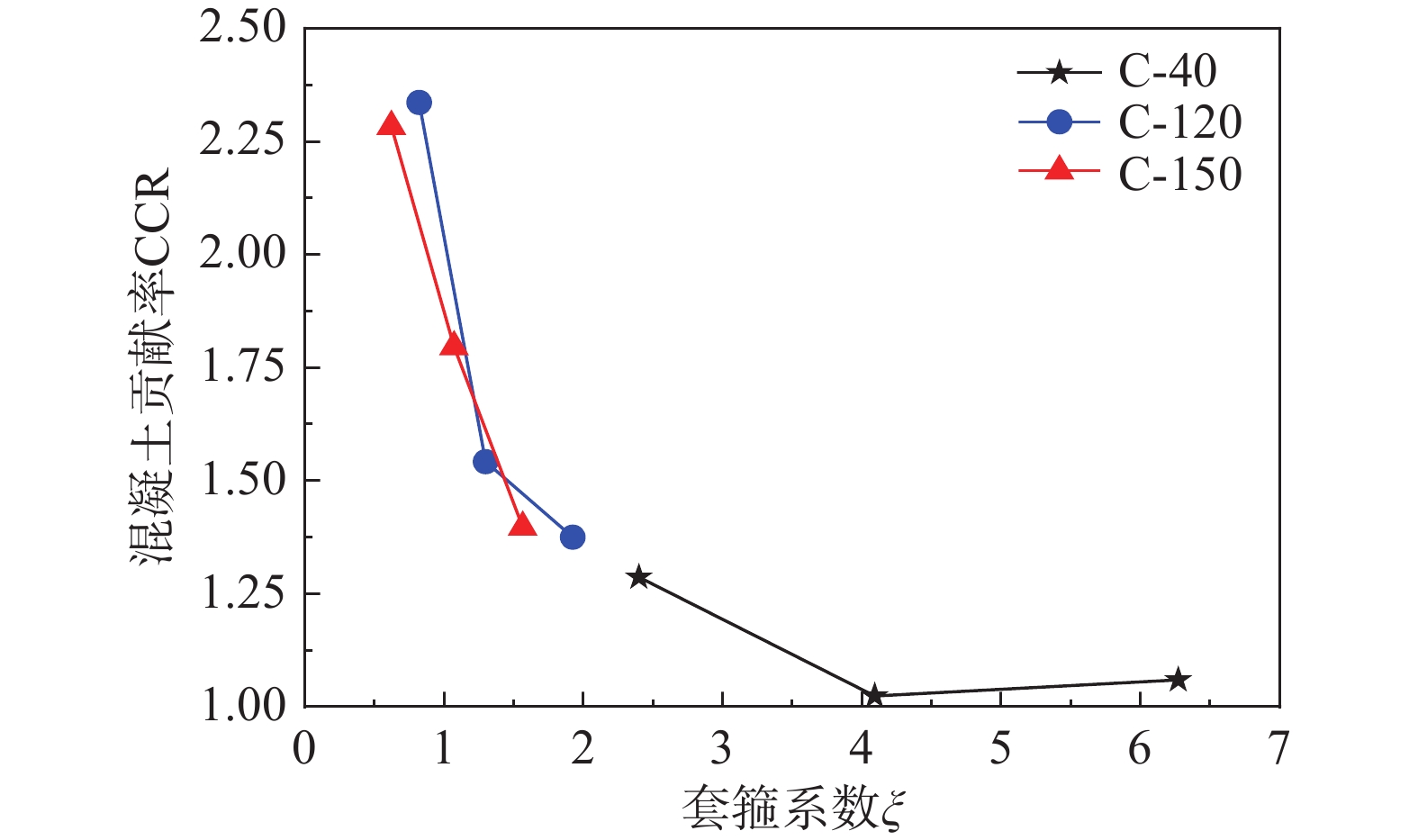
混凝土贡献率(CCR)是评价CFST核心混凝土强度提高指标，定义如下^[20]：

${\rm{CCR}} = \frac{{{N_{{\rm{u}}}}}}{{{N_{\rm{h}}}}}$

(2)

式中，N_h为空钢管的极限抗压强度试验值。CCR与 $\xi$ 的关系如所示，在4 mm系列中，当 $\xi$ 从0.603增大到2.399，CCR减小了43.6%；在6 mm系列中，当 $\xi$ 从1.034增大到4.092，CCR减小了43%；在8 mm系列中，当 $\xi$ 从1.564增大到6.272，CCR减小了24.1%，由此可以发现UHPC贡献率大于C40。相同混凝土等级，随着套箍系数增大混凝土贡献率降低，这是由于较薄不锈钢管较早的发生局部屈曲，限制了不锈钢管对混凝土的约束作用。

图 7 混凝土贡献率(CCR)与约束因子(

$\xi$ )的关系

Figure 7. Concrete contribution ratio (CCR) versus confinement factor (

$\xi$ ) relationship

下载: 全尺寸图片幻灯片

2.4.2 强度提高系数

混凝土强度提高系数CSI可以定量评价钢管与混凝土的复合作用对CFST柱截面抗力的影响，其定义式如下^[17]：

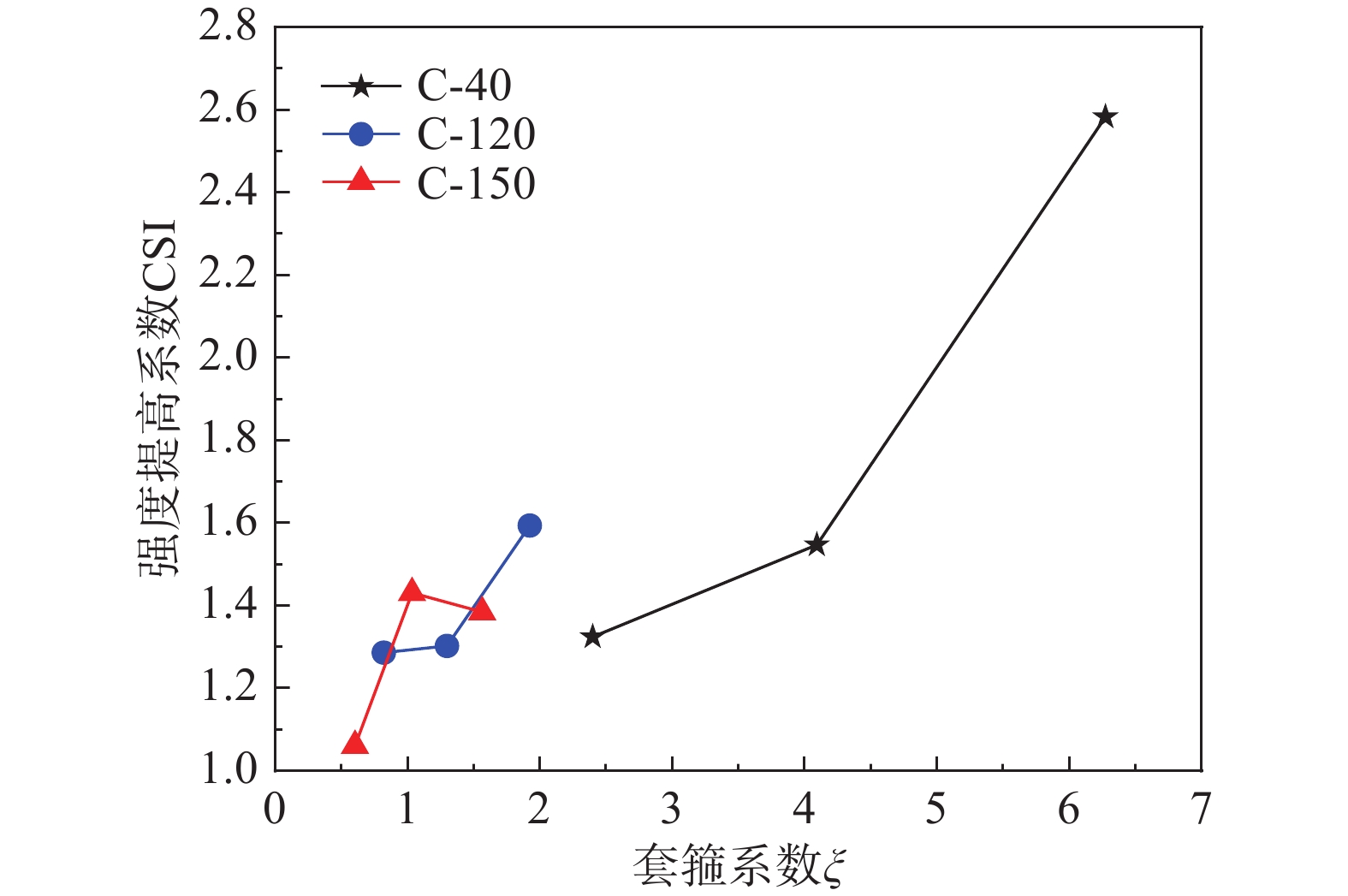
${\rm{CSI}} = \frac{{{N_{{\rm{u}}}} - {f_{\rm{y}}}{A_{{\rm{s}}}}}}{{{f_{{\rm{c}}}}{A_{{\rm{c}}}}}}$

(3)

试件的CSI如所示，试件强度提高系数CSI变化范围为1.061~1.593，试件承载力大于不锈钢管与混凝土承载力之和，表明不锈钢管与混凝土均发挥了材料的特性，不锈钢管起到了良好的约束作用。各试件CSI与套箍系数 $\xi$ 的关系如图8所示。相同混凝土等级下，随着套箍系数的增大，CSI呈增大趋势。

图 8 混凝土强度指标(CSI)与约束因子(

$\xi$ )的关系

Figure 8. Concrete strength index (CSI) versus confinement factor (

$\xi$ ) relationship

下载: 全尺寸图片幻灯片

在4 mm系列试件中，当 $\xi$ 从0.603增加到2.399，CSI降低了24.5%；在6 mm系列试件中，当 $\xi$ 从1.034增加到4.092，CSI降低了18.5%；在8 mm系列试件中，当 $\xi$ 从1.564增加到6.272，CSI降低了87%。表明混凝土等级越高，混凝土强度提高系数越小。上述现象与文献[22]指出的规律一致，是因为：1) UHPC明显的自收缩特性及UHPC的内部缺陷，如存在的微孔洞、微裂纹，导致不锈钢管与UHPC粘结性能较差，从而削弱横截面的复合效应；2) 混凝土材料的多轴力学性能特性，当围压相同时，混凝土等级越大，单轴强度越大，围压与单轴强度之比越小，围压对多轴强度提高也越小，因此普通混凝土的强度提高系数大于UHPC的强度提高系数。

3 承载力计算模型

3.1 现行规范对比

现行普通碳钢管混凝土的计算方法的适用范围及计算式见表7：日本规范(AIJ-CFT)^[33]、欧洲规范(Eurocode 4)^[34]、美国钢结构规范(ANSI/AISC 360-10−2020)^[35]以及国内规程(CECS 28: 2012)^[36]。

当前缺乏对UHPC填充不锈钢管的设计方法，借鉴现行普通碳钢管混凝土计算方法计算试件极限承载力，图9显示采用各规范计算的承载力结果与偏差，其中MV为平均值，SD为标准差。Eurocode 4的平均值为1.406，标准差为0.076；ANSI/AISC 360-10−2020的平均值为1.216，标准差为0.057；AIJ-CFT的平均值为1.036，标准差为0.063。国外规范给出的计算结果偏保守，试验结果高出规范计算承载力的41.7%、22.4%和4.4%；而CECS 28: 2012的平均值为0.905，标准差为0.052，给出了偏不安全的计算结果，高估了承载力10.4%，且预测结果离散性较大。国外规范预测结果偏于保守是因为不锈钢管与核心混凝土复杂的相互作用，加载初期，钢管与混凝土共同受力，到加载后期，不锈钢管纵向分担的荷载减少，通过约束使核心混凝土承担更多的荷载，国外规范采用叠加原理不能良好预测加载后期不锈钢管对超高性能混凝土的约束作用，并且UHPC出现裂缝后，由于钢纤维的桥接效应，导致荷载重分布，难以计算不锈钢管与UHPC后期的荷载分配，故预测结果出现一定的偏差。而中国规程CECS 28: 2012引入了套箍系数，考虑了钢管与混凝土的相互作用，但混凝土等级远远超出规范范围，导致离散性较大，预测结果偏于不安全。

表 7 与钢管混凝土相关的各规范适用范围

Table 7. Application range of specifications relating to concrete filled steel tube

规范	计算式	D/t范围	f_c范围	f_y范围
AIJ-CFT	${N_{\rm{AIJ} } } = 1.27{A_{\rm{s} } }{f_{\rm{y} } } + 0.85{A_{{\rm{c}}} }f_{{\rm{c}}}'$	$1.5 \times \dfrac{{{{240}}}}{{F/{{98}}}}$ $F = {\rm{min}}( { {f_{\rm{y} } },0.7{f_{\rm{u} } } } )$	${\leqslant} {{90\;{\rm{ MPa}}}}$	${\leqslant} {{590\;{\rm{ MPa}}}}$
Eurocode 4	${N_{\rm{EC4} } } = \dfrac{ { {f_{\rm{y} } } }}{ { {\gamma _{\rm{s} } } }}{A_{\rm{s} } } + \dfrac{ {f_{{\rm{c}}}'} }{ { {\gamma _{{\rm{c}}} } } }{A_{{\rm{c}}} }$	${{90}} \times {{235}}/{f_{\rm{y}}}$	${\leqslant} {{75\;{\rm{ MPa}}}}$	${\leqslant} {{460\;{\rm{ MPa}}}}$
ANSI/AISC 360-10−2020	${N_{{\rm{AISC}}}} = {A_{\rm{s}}}{f_{\rm{y}}} + {{0}}{{.85}}{A_{\rm{c}}}f_{\rm{c}}'$	${{2}}{{.26}}\sqrt {{E_{\rm{s}}}/{f_{\rm{y}}}}$	${\leqslant} {{70\;{\rm{ MPa}}}}$	${\leqslant} {{525\;{\rm{ MPa}}}}$
CECS 28: 2012	${N_{\rm{u}}} = {\varphi _1}{\varphi _{{e}}}{N_0}$ ${N_0} = \left\{ {\begin{array}{*{20}{l} } { { {0} }{ {.9} }{A_{\rm{c} } }{f_{\rm{c} } }( {1 + \alpha \theta } ),{ {0} }{ {.5} } < \theta {\leqslant} \left[ \theta \right]} \\ { { {0} }{ {.9} }{A_{\rm{c} } }{f_{\rm{c} } }( { { {1} } + \sqrt \theta + \theta } ),\left[ \theta \right] < \theta < { {2} }{ {.5} } } \end{array} } \right.$	$\dfrac{{( {20\sim 135} ){{235}}}}{{{f_{\rm{y}}}}}$ ${{0}}{{.5}} {\leqslant} \theta {\leqslant} {{2}}{{.5}}$	${\leqslant} {{80\;{\rm{ MPa}}}}$	${\leqslant} {{460\;{\rm{ MPa}}}}$
注： $f_{\mathrm{c}}^{\prime}$ 为土圆柱体抗压强度；f_y为材屈服强度，本文取名义屈服强度f_0.2合截面面积，A_sc=A_s+A_c； ${\gamma _{\rm{s}}}$ 为钢材的材料分项系数，取1.1； γ_c为混凝土的材料分项系数，取1.5；混凝土等级小于C50时，α=2.0，等级在C50~C80之间时，α=1.8；[θ]为与混凝土等级有关的套箍指标界限值。

下载: 导出CSV

| 显示表格

图 9 各规范计算结果对比

Figure 9. Comparison of calculation results of various specifications

下载: 全尺寸图片幻灯片

3.2 基于设计的承载力计算模型

由于目前缺乏适用于UFCSST的承载力计算模型，本文根据统一强度理论推导UFCSST的承载力计算模型。由构件受力可知，核心混凝土处于三向受压状态，不锈钢管处于轴向受压、环向受拉和径向受压的应力状态。UFCSST承载力由约束核心混凝土的轴向承载力N_cc、不锈钢管承载力N_s，其表达式为：

$N = {N_{{\text{cc}}}} + {N_{{\rm{s}}}}$

(4)

3.2.1 不锈钢应力

假定材料为理想塑性不可压缩，不锈钢管内表面压力均匀分布，采用统一强度理论^[37]计算不锈钢管壁受到的径向压力P_s：

${P_{\text{s}}} = \frac{{{f_{{\text{0}}{\text{.2}}}}}}{{{\text{1}} - \alpha }}\left[ {{{\left( {\frac{{{r_{\text{i}}}}}{{{r_{\text{o}}}}}} \right)}^{\frac{{{\text{2}}\left( {{\text{1}} + b} \right)\left( {\alpha - {\text{1}}} \right)}}{{{\text{2}} + {\text{2}}b - \alpha b}}}} - 1} \right]$

(5)

式中：α为不锈钢管的拉压比；b为主应力对材料破坏影响程度的材料强度参数；r_o为不锈钢管的外径；r_i为不锈钢管的内径。

本文采用双相不锈钢管，α取1，b为0，得到单剪屈服准则线性逼近式：

${P_{\text{s}}} = - {f_{{\text{0}}{\text{.2}}}}\ln\frac{{{r_{\text{i}}}}}{{{r_{\text{o}}}}}$

(6)

由厚壁圆筒原理^[37]，可得不锈钢管轴向抗压强度f_s，其表达式为：

${f_{\rm{s}}} = \frac{{{P_{\rm{s}}}r_{\rm{i}}^2}}{{r_{\rm{o}}^2 - r_{\rm{i}}^2}}$

(7)

3.2.2 混凝土应力

混凝土承受轴向荷载与不锈钢管产生的侧向主动约束作用，处于三向受压状态，致使UHPC轴向抗压强度有所提升。其提升后的抗压强度f_cc与所受的围压线性相关，符合Mohr-Coulomb破坏准则，其表达式为：

$\frac{{{\sigma_1}}}{{{f_{\rm{c}}}}} = 1 + k\frac{{{\sigma_3}}}{{{f_{\rm{c}}}}}$

(8)

式中：σ₁为第一主应力；σ₃为第三主应力；k为有效侧向压力系数。

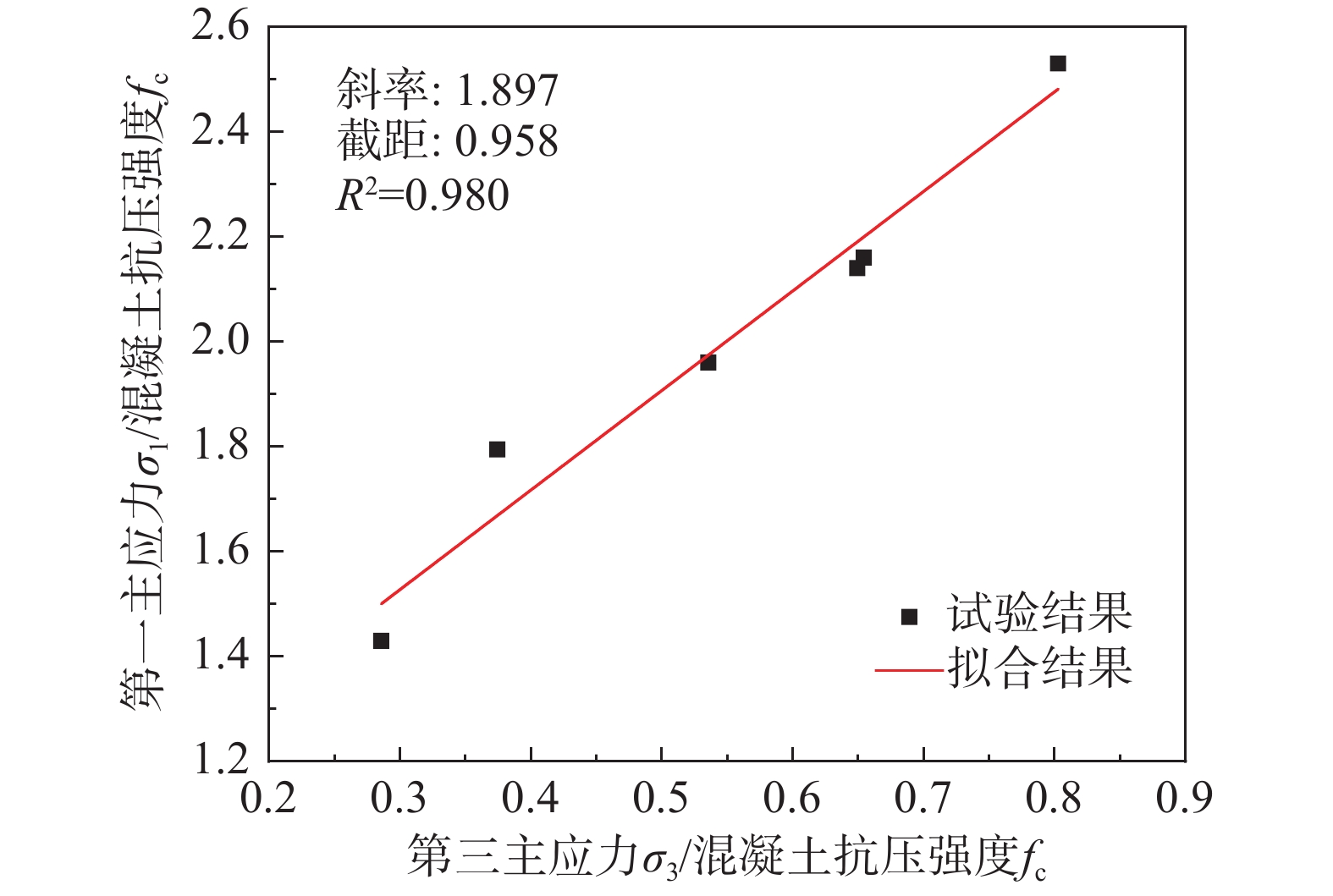
根据本文试验结果对有效侧向压力系数进行线性拟合如图10所示。

图 10 k值拟合结果

Figure 10. Fitting result of k value

下载: 全尺寸图片幻灯片

普通混凝土有效侧向压力系数为4^[38]，而由于UHPC抗压强度高且内含钢纤维，混凝土开裂后钢纤维能够提供被动约束作用，减缓裂缝开展和横向变形，因此有效侧向压力系数较小，根据图10线性拟合结果有效侧向压力系数k为1.897。

因此，主动约束与被动约束同时作用下，UHPC轴向抗压强度f_cc计算式如下：

${f_{\rm{cc}}} = 0.958{f_{\rm{c}}}{A_{\rm{c}}} + 1.897{P_{\rm{s}}}$

(9)

3.2.3 承载力计算模型

式(5)中：

${N_{{\text{cc}}}} = {f_{{\text{cc}}}}{A_{\text{c}}}$

(10)

${N_{\text{s}}} = {f_{\text{s}}}{A_{\text{s}}}$

(11)

式中：A_s为不锈钢横截面面积；A_c为核心混凝土截面面积，将式(6)~式(12)代入式(5)可得承载力N最终计算式：

$\begin{split} N = &0.958{f_{\rm{c}}}{A_{\rm{c}}} - 1.897{f_{{0}{.2}}}\ln \frac{{{r_{\rm{i}}}}}{{{r_{\rm{o}}}}}{A_{\rm{c}}} - \frac{{r_{\rm{i}}^2{f_{0.2}}}}{{r_{\rm{o}}^2 - r_{\rm{i}}^2}}\ln \frac{{{r_{\rm{i}}}}}{{{r_{\rm{o}}}}}{A_{\rm{s}}} \end{split}$

(12)

表8给出了采用AIJ、Eurocode 4、ANSI/AISC 360-10−2020和CECS 28: 2012计算方法所得试件截面承载力以及试验结果的对比情况。由表8可知，式(13)计算结果的MV为0.994，SD为0.007。采用式(13)的计算结果与试验结果吻合较好。

表 8 UFCSST承载力计算值与实验结果对比

Table 8. Comparisons of calculated and experimental results

试件编号	N_u/kN	本文计算模型		AIJ		Eurocode 4		ANSI/AISC 360-10−2020		CECS 28: 2012
试件编号	N_u/kN	N/kN	N_u/N	N/kN	N_u/N	N/kN	N_u/N	N/kN	N_u/N	N/kN	N_u/N
C-120-4	2201	2207	1.003	1976	1.114	1457	1.492	1745	1.261	2328	0.945
C-120-6	2612	2671	1.022	2392	1.041	1769	1.408	2057	1.211	2976	0.866
C-120-8	3096	2734	1.883	2844	1.068	2086	1.456	2396	1.268	3351	0.906
C-150-4	2146	2447	1.140	2088	1.030	1570	1.370	1878	1.146	2425	0.886
C-150-6	2902	2910	1.003	2509	1.140	1864	1.534	2186	1.308	2987	0.957
C-150-8	3215	2941	0.915	2979	1.040	2194	1.411	2536	1.221	3607	0.859
MV	−	−	0.994	−	1.036	−	1.406	−	1.216	−	0.905
SD	−	−	0.007	−	0.063	−	0.076	−	0.057	−	0.052
注：N为承载力计算值；N_u为实际承载力。

下载: 导出CSV

| 显示表格

4 结论

基于本文的试验数据和已有文献的研究成果分析，初步得出以下结论：

(1) UFCSST的核心混凝土破坏模式与套箍系数相关。在外钢管屈曲处，超高性能混凝土在端部鼓曲部分挤压明显，外部混凝土剥落，中部混凝土出现剪切裂纹。套箍系数越大，混凝土从出现剪切裂纹到横向膨胀转变。

(2) 荷载-位移曲线依据套箍系数可分为三类： $\xi$ =0.82，存在下降段，强化阶段曲线逐渐恢复至峰值荷载；1.03 ${\leqslant }\xi {\leqslant }$ 1.30，下降段不明显或不存在，强化阶段曲线平稳发展； $\xi {\geqslant }$ 1.30，不存在下降段，强化阶段曲线在极限荷载基础上缓慢上升。

(3) 提供核心混凝土合适的围压，增大套箍系数可有效提高组合柱的承载力；UHPC中的钢纤维在混凝土开裂后提供额外摩擦阻力以及不锈钢管应变硬化效应，能在强化阶段使试件承载力有所上升。

(4)普通混凝土强度提高系数明显大于超高性能混凝土强度提高系数。混凝土强度提高系数与套箍系数相关，相同混凝土等级，套箍系数越大，强度提高系数越大。填充UHPC在一定程度上能够提升UFCSST的承载力能力，但提升UHPC等级对承载力贡献不大，如： C-150-6比C-120-6承载力提升了14.8%。

(5) 国外现行规范采用叠加原理，预测结果较为保守，国内现行规程虽考虑了混凝土与钢管的相互作用，但UHPC等级远远超出规范范围，预测结果偏于不安全。本文基于统一强度理论提出了UFCSST基于设计的承载力计算模型。但缺乏相关实验数据，设计模型有待进一步验证。

图 1 不锈钢拉伸应力-应变试验曲线

Figure 1. Tensile stress-strain experimental curves of steel

下载: 全尺寸图片幻灯片

图 2 加载系统和测点布置

Figure 2. Loading system and arrangement of measuring points

下载: 全尺寸图片幻灯片

图 3 试件破坏形态

Figure 3. Specimen failure mode

下载: 全尺寸图片幻灯片

图 4 UHPCFSST荷载-位移曲线

Figure 4. UHPCFSST load-displacement curve

下载: 全尺寸图片幻灯片

图 5 极限荷载对比

Figure 5. Comparison of ultimate load

下载: 全尺寸图片幻灯片

图 6 试件的荷载-应变曲线

Figure 6. Load-strain curves of specimens

下载: 全尺寸图片幻灯片

混凝土贡献率(CCR)与约束因子( $\xi$ )的关系

Concrete contribution ratio (CCR) versus confinement factor ( $\xi$ ) relationship

下载: 全尺寸图片幻灯片

混凝土强度指标(CSI)与约束因子( $\xi$ )的关系

Concrete strength index (CSI) versus confinement factor ( $\xi$ ) relationship

下载: 全尺寸图片幻灯片

图 9 各规范计算结果对比

Figure 9. Comparison of calculation results of various specifications

下载: 全尺寸图片幻灯片

图 10 k值拟合结果

Figure 10. Fitting result of k value

下载: 全尺寸图片幻灯片

表 1 试件的详细参数

Table 1 Detailed parameters of the specimen

试件编号	D/mm	L/mm	t/mm	f_c/MPa	f_0.2/MPa
C-0-4	114.5	342.1	4.2	−	558.7
C-0-6	112.3	341.5	6.2	−	641.0
C-0-8	114.3	341.9	9.2	−	546.7
C-40-4	114.3	342.5	4.0	36.7	558.7
C-40-6	113.5	342.0	6.3	36.7	641.0
C-40-8	114.2	342.0	9.2	36.7	546.7
C-120-4	114.4	342.5	4.4	119.4	558.7
C-120-6	114.1	342.2	6.5	119.4	641.0
C-120-8	114.4	341.9	9.2	119.4	546.7
C-150-4	114.8	342.5	4.1	144.9	558.7
C-150-6	114.0	341.9	6.5	144.9	641.0
C-150-8	114.3	342.5	9.1	144.9	546.7
注：D为试件的实测外径；L为柱的实测高度；t为不锈钢管实测壁厚；f_c为圆柱体抗压强度；f_0.2为不锈钢名义屈服应力。

下载: 导出CSV

表 2 UHPC配合比

Table 2 Mix proportions of UHPC /(kg·m⁻³)

成分	胶凝材料	石英砂	水	高性能减水剂	钢纤维
含量	1035.6	1035.6	184.7	13/16	181
注：UHPC-120和UHPC-150采用不同的预混凝料(胶凝材料和石英砂)，配合比中仅高性能减水剂含量不同，分别为13 kg·m⁻³和16 kg·m⁻³。

下载: 导出CSV

表 3 钢纤维参数表

Table 3 Properties of steel fiber

长度 /mm	直径/mm	长径比	密度/(kg·m⁻³)	极限强度/MPa	弹性模量/GPa
13	0.2	65	7900	2900	200

下载: 导出CSV

表 4 混凝土材料性能

Table 4 Performance of concrete material

混凝土等级	混凝土立方体抗压强度f_cu/MPa	圆柱体抗压强度f_c/MPa	弹性模量E_c/MPa
C40	44.0	36.7	32 500
UHPC-120	129.2	119.4	44 200
UHPC-150	154.3	144.9	44 800

下载: 导出CSV

表 5 钢材力学性能指标

Table 5 Mechanical properties of steel

钢管名义厚度	f_0.2/MPa	f_u/MPa	E₀/GPa
4 mm	558.7	646.0	182.9
6 mm	566.0	728.6	183.6
8 mm	546.7	647.4	183.7
注：E₀为弹性模量；f_0.2为不锈钢名义屈服应力；f_u为极限抗拉强度。表中数值均为平均值。

下载: 导出CSV

表 6 试验结果汇总表

Table 6 Test results summary

试样标签	D/t	N_u/kN	$\xi$	CCR	CSI
C-0-4	27.3	942	−	−	−
C-0-6	18.1	1615	−	−	−
C-0-8	12.4	2209	−	−	−
C-40-4	28.6	1212	2.399	1.287	1.095
C-40-6	18.0	1654	4.092	1.024	1.107
C-40-8	12.4	2341	6.272	1.059	1.218
C-120-4	26.0	2201	0.820	2.337	1.157
C-120-6	17.6	2612	1.297	1.542	1.132
C-120-8	12.4	3096	1.923	1.375	1.203
C-150-4	28.0	2146	0.603	2.283	1.038
C-150-6	17.5	2902	1.034	1.796	1.229
C-150-8	12.6	3215	1.564	1.397	1.146
注：N_u为试件实测极限承载力，若荷载-位移曲线无下降段，取纵向应变达到0.01时对应的荷载^[32]；ξ为套箍系数；CCR为混凝土贡献率；CSI为混凝土强度提高系数；D/t为试件的实测外径与不锈钢管实测壁厚之比。

下载: 导出CSV

表 7 与钢管混凝土相关的各规范适用范围

Table 7 Application range of specifications relating to concrete filled steel tube

规范	计算式	D/t范围	f_c范围	f_y范围
AIJ-CFT	${N_{\rm{AIJ} } } = 1.27{A_{\rm{s} } }{f_{\rm{y} } } + 0.85{A_{{\rm{c}}} }f_{{\rm{c}}}'$	$1.5 \times \dfrac{{{{240}}}}{{F/{{98}}}}$ $F = {\rm{min}}( { {f_{\rm{y} } },0.7{f_{\rm{u} } } } )$	${\leqslant} {{90\;{\rm{ MPa}}}}$	${\leqslant} {{590\;{\rm{ MPa}}}}$
Eurocode 4	${N_{\rm{EC4} } } = \dfrac{ { {f_{\rm{y} } } }}{ { {\gamma _{\rm{s} } } }}{A_{\rm{s} } } + \dfrac{ {f_{{\rm{c}}}'} }{ { {\gamma _{{\rm{c}}} } } }{A_{{\rm{c}}} }$	${{90}} \times {{235}}/{f_{\rm{y}}}$	${\leqslant} {{75\;{\rm{ MPa}}}}$	${\leqslant} {{460\;{\rm{ MPa}}}}$
ANSI/AISC 360-10−2020	${N_{{\rm{AISC}}}} = {A_{\rm{s}}}{f_{\rm{y}}} + {{0}}{{.85}}{A_{\rm{c}}}f_{\rm{c}}'$	${{2}}{{.26}}\sqrt {{E_{\rm{s}}}/{f_{\rm{y}}}}$	${\leqslant} {{70\;{\rm{ MPa}}}}$	${\leqslant} {{525\;{\rm{ MPa}}}}$
CECS 28: 2012	${N_{\rm{u}}} = {\varphi _1}{\varphi _{{e}}}{N_0}$ ${N_0} = \left\{ {\begin{array}{*{20}{l} } { { {0} }{ {.9} }{A_{\rm{c} } }{f_{\rm{c} } }( {1 + \alpha \theta } ),{ {0} }{ {.5} } < \theta {\leqslant} \left[ \theta \right]} \\ { { {0} }{ {.9} }{A_{\rm{c} } }{f_{\rm{c} } }( { { {1} } + \sqrt \theta + \theta } ),\left[ \theta \right] < \theta < { {2} }{ {.5} } } \end{array} } \right.$	$\dfrac{{( {20\sim 135} ){{235}}}}{{{f_{\rm{y}}}}}$ ${{0}}{{.5}} {\leqslant} \theta {\leqslant} {{2}}{{.5}}$	${\leqslant} {{80\;{\rm{ MPa}}}}$	${\leqslant} {{460\;{\rm{ MPa}}}}$
注： $f_{\mathrm{c}}^{\prime}$ 为土圆柱体抗压强度；f_y为材屈服强度，本文取名义屈服强度f_0.2合截面面积，A_sc=A_s+A_c； ${\gamma _{\rm{s}}}$ 为钢材的材料分项系数，取1.1； γ_c为混凝土的材料分项系数，取1.5；混凝土等级小于C50时，α=2.0，等级在C50~C80之间时，α=1.8；[θ]为与混凝土等级有关的套箍指标界限值。

下载: 导出CSV

表 8 UFCSST承载力计算值与实验结果对比

Table 8 Comparisons of calculated and experimental results

试件编号	N_u/kN	本文计算模型		AIJ		Eurocode 4		ANSI/AISC 360-10−2020		CECS 28: 2012
试件编号	N_u/kN	N/kN	N_u/N	N/kN	N_u/N	N/kN	N_u/N	N/kN	N_u/N	N/kN	N_u/N
C-120-4	2201	2207	1.003	1976	1.114	1457	1.492	1745	1.261	2328	0.945
C-120-6	2612	2671	1.022	2392	1.041	1769	1.408	2057	1.211	2976	0.866
C-120-8	3096	2734	1.883	2844	1.068	2086	1.456	2396	1.268	3351	0.906
C-150-4	2146	2447	1.140	2088	1.030	1570	1.370	1878	1.146	2425	0.886
C-150-6	2902	2910	1.003	2509	1.140	1864	1.534	2186	1.308	2987	0.957
C-150-8	3215	2941	0.915	2979	1.040	2194	1.411	2536	1.221	3607	0.859
MV	−	−	0.994	−	1.036	−	1.406	−	1.216	−	0.905
SD	−	−	0.007	−	0.063	−	0.076	−	0.057	−	0.052
注：N为承载力计算值；N_u为实际承载力。

下载: 导出CSV

参考文献(38)

[1]	DEWANBABEE H, DAS S. Structural behavior of corroded steel pipes subject to axial compression and internal pressure: Experimental study [J]. Journal of Structural Engineering, 2013, 139(1): 57 − 65. doi: 10.1061/(ASCE)ST.1943-541X.0000596
[2]	LAM D, GARDNER L. Structural design of stainless steel concrete filled columns [J]. Journal of Constructional Steel Research, 2008, 64(11): 1275 − 1282. doi: 10.1016/j.jcsr.2008.04.012
[3]	DABAON M A, EL-BOGHDADI M H, HASSANEIN M F. Experimental investigation on concrete-filled stainless steel stiffened tubular stub columns [J]. Engineering Structures, 2009, 31(2): 300 − 307. doi: 10.1016/j.engstruct.2008.08.017
[4]	UY B, TAO Z, HAN L H. Behaviour of short and slender concrete-filled stainless steel tubular columns [J]. Journal of Constructional Steel Research, 2011, 67(3): 360 − 378. doi: 10.1016/j.jcsr.2010.10.004
[5]	DAI P, YANG L, WANG J, et al. Compressive strength of concrete-filled stainless steel tube stub columns [J]. Engineering Structures, 2020, 205: 110106. doi: 10.1016/j.engstruct.2019.110106
[6]	AN H, WANG F Y, ZHAO O. Experimental and numerical studies of concrete-filled high-chromium stainless steel tube (CFHSST) stub columns [J]. Thin-Walled Structures, 2019, 144: 106273. doi: 10.1016/j.tws.2019.106273
[7]	代鹏, 杨璐, 卫璇, 等. 不锈钢管混凝土短柱轴压承载力试验研究[J]. 工程力学, 2019, 36(增刊 1): 298 − 305. doi: 10.6052/j.issn.1000-4750.2018.05.S065 DAI Peng, YANG Lu, WEI Xuan, et al. Experimental studies on the behavior and capacity of concrete filled stainless steel tube short columns [J]. Engineering Mechanics, 2019, 36(Suppl 1): 298 − 305. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S065
[8]	唐红元, 范璐瑶, 赵鑫, 等. 圆不锈钢管混凝土短柱轴压承载力性能研究[J]. 地震工程与工程振动, 2021, 41(1): 63 − 69. doi: 10.13197/j.eeev.2021.01.63.tanghy.008 TANG Hongyuan, FAN Luyao, ZHAO Xin, et al. Study on bearing capacity of concrete-filled circular stainless steel tubular stub columns under axial compression [J]. Earthquake Engineering and Engineering Dynamics, 2021, 41(1): 63 − 69. (in Chinese) doi: 10.13197/j.eeev.2021.01.63.tanghy.008
[9]	唐红元, 范璐瑶, 赵鑫, 等. 圆不锈钢管混凝土短柱轴压承载力模型研究[J]. 工程科学与技术, 2020, 52(3): 10 − 20. TANG Hongyuan, FAN Luyao, ZHAO Xin, et al. Bearing capacity model of circular concrete-filled stainless steel stub columns under uniaxial compression [J]. Advanced Engineering Sciences, 2020, 52(3): 10 − 20. (in Chinese)
[10]	LEE S H, UY B, KIM S H, et al. Behavior of high-strength circular concrete-filled steel tubular (CFST) column under eccentric loading [J]. Journal of Constructional Steel Research, 2011, 67(1): 1 − 13. doi: 10.1016/j.jcsr.2010.07.003
[11]	SONG P S, WU J C, HWANG S, et al. Assessment of statistical variations in impact resistance of high-strength concrete and high-strength steel fiber-reinforced concrete [J]. Cement and Concrete Research, 2005, 35(2): 393 − 399. doi: 10.1016/j.cemconres.2004.07.021
[12]	LU Y Y, LI N, LI S, et al. Behavior of steel fiber reinforced concrete-filled steel tube columns under axial compression [J]. Construction and Building Materials, 2015, 95: 74 − 85. doi: 10.1016/j.conbuildmat.2015.07.114
[13]	QI J N, WANG J Q, Ma Z J. Flexural response of high-strength steel-ultra-high-performance fiber reinforced concrete beams based on a mesoscale constitutive model: Experiment and theory [J]. Structural Concrete, 2018, 19(3): 719 − 734. doi: 10.1002/suco.201700043
[14]	QI J N, MA Z J, WANG J Q, et al. Post-cracking shear strength and deformability of HSS-UHPFRC beams [J]. Structural Concrete, 2016, 17(6): 1033 − 1046. doi: 10.1002/suco.201500191
[15]	王秋维, 梁林, 王程伟, 等. 圆钢管超高性能混凝土短柱偏压力学性能研究[J]. 应用力学学报, 2024, 41(3): 536 − 545. doi: 10.11776/i.issn.1000-4939.2024.03.006 WANG Qiuwei, LIANG Lin, WANG Chengwei, et al. The eccentric compression performance of ultra-high performance concrete filled with circular steel tube short columns [J]. Chinese Journal of Applied Mechanics, 2024, 41(3): 536 − 545. (in Chinese) doi: 10.11776/i.issn.1000-4939.2024.03.006
[16]	廖飞宇, 陶忠. 不锈钢管混凝土的发展综述[J]. 工业建筑, 2009, 39(4): 114 − 118. doi: 10.13204/j.gyjz2009.04.032 LIAO Feiyu, TAO Zhong. The state-of-the-art of concrete-filled stainless steel tubular structures [J]. Industrial Construction, 2009, 39(4): 114 − 118. (in Chinese) doi: 10.13204/j.gyjz2009.04.032
[17]	王彦博, 宋辞, 赵星源, 等. 高强圆钢管混凝土短柱轴压承载力试验研究[J]. 建筑结构学报, 2022, 42(11): 221 − 234. WANG Yanbo, SONG Ci, ZHAO Xingyuan, et al. Experimental study on behavior of circular concrete-filled high-strength steel tubular stub columns under compression [J]. Journal of Building Structures, 2022, 42(11): 221 − 234. (in Chinese)
[18]	WANG Y Z, WANG Y B, ZHAO Y Z, et al. Experimental study on ultra-high performance concrete under triaxial compression [J]. Construction and Building Materials, 2020, 263: 120225. doi: 10.1016/j.conbuildmat.2020.120225
[19]	GULER S, ÇOPUR A, AYDOGAN M. Axial capacity and ductility of circular UHPC-filled steel tube columns [J]. Magazine of Concrete Research, 2013, 65(15): 898 − 905. doi: 10.1680/macr.12.00211
[20]	CHEN S M, RUI Z, JIA L J, et al. Structural behavior of UHPC filled steel tube columns under axial loading [J]. Thin-Walled Structures, 2018, 130(5): 550 − 563.
[21]	XU L H, LU Q R, CHI Y, et al. Axial compressive performance of UHPC filled steel tube stub columns containing steel-polypropylene hybrid fiber [J]. Construction and Building Materials, 2019, 204: 754 − 767. doi: 10.1016/j.conbuildmat.2019.01.202
[22]	吴兆旗, 魏源, 王鑫涛, 等. 局部锈蚀圆钢管构件轴压力学性能正交试验研究[J]. 工程力学, 2020, 37(4): 144 − 152. doi: 10.6052/j.issn.1000-4750.2019.06.0327 WU Zhaoqi, WEI Yuan, WANG Xintao, et al. Orthogonal experimental study on axial mechanical behavior of locally corroded circular steel tubes [J]. Engineering Mechanics, 2020, 37(4): 144 − 152. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.06.0327
[23]	徐吉民, 幸坤涛, 高向宇, 等. 锈损冷弯薄壁卷边槽钢短柱受压承载力试验研究[J]. 工程力学, 2021, 38(4): 191 − 199, 210. doi: 10.6052/j.issn.1000-4750.2020.06.0376 XU Jimin, XING Kuntao, GAO Xiangyu, et al. Experimental investigation on compressive bearing capacity of cold-formed thin-walled lipped channel short columns with corrosion [J]. Engineering Mechanics, 2021, 38(4): 191 − 199, 210. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0376
[24]	唐红元, 李政周, 范璐瑶, 等. 矩形不锈钢管混凝土短柱轴压性能试验研究[J]. 西南交通大学学报, 2022, 57(4): 855 − 864. doi: 10.3969/j.issn.0258-2724.20200416 TANG Hongyuan, LI Zhengzhou, FAN Luyao, et al. Experimental investigation on behavior of rectangular concrete-filled stainless steel tubular stub columns under axial loading [J]. Journal of Southwest Jiaotong University, 2022, 57(4): 855 − 864. (in Chinese) doi: 10.3969/j.issn.0258-2724.20200416
[25]	GB/T 31387−2015, 活性粉末混凝土[S]. 北京: 中国标准出版社, 2015. GB/T 31387−2015, Reactive powder concrete [S]. Beijing: Standards Press of China, 2015. (in Chinese)
[26]	GB/T 50081−2019, 普通混凝土力学性能试验方法标准[S]. 北京: 中国建筑工业出版社, 2003. GB/T 50081−2019, Standard for test method of mechanical properties on ordinary concrete [S]. Beijing: China Architecture & Building Press, 2003. (in Chinese)
[27]	ZHONG T, WANG Z B, YU Q. Finite element modelling of concrete-filled steel stub columns under axial compression [J]. Journal of Constructional Steel Research, 2013, 89: 121 − 131. doi: 10.1016/j.jcsr.2013.07.001
[28]	GB 50010−2010, 混凝土结构设计规范(2015年版)[S]. 北京: 中国建筑工业出版社, 2011. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[29]	GB/T 228.1−2010, 金属材料拉伸试验第1部分: 室温试验方法[S]. 北京: 中国标准出版社, 2011. GB/T 228.1−2010, Metallic materials-tensile testing-part 1: Method of test at room temperature [S]. Beijing: Standards Press of China, 2011. (in Chinese)
[30]	戎芹, 曾宇声, 侯晓萌, 等. 圆钢管钢纤维活性粉末混凝土短柱轴压性能试验研究[J]. 建筑结构学报, 2019, 40(3): 247 − 253. doi: 10.14006/j.jzjgxb.2019.03.026 RONG Qin, ZENG Yusheng, HOU Xiaomeng, et al. Experimental study on mechanical behavior of RPC-filled circular steel tube columns under axial compression [J]. Journal of Building Structures, 2019, 40(3): 247 − 253. (in Chinese) doi: 10.14006/j.jzjgxb.2019.03.026
[31]	WEI J G, XIE Z T, ZHANG W, et al. Experimental study on circular steel tube-confined reinforced UHPC columns under axial loading [J]. Engineering Structures, 2021, 230: 111599. doi: 10.1016/j.engstruct.2020.111599
[32]	张素梅, 李孝忠, 卢炜, 等. 钢管约束的钢管混凝土短柱轴压性能试验研究[J]. 建筑结构学报, 2022, 43(6): 21 − 33. doi: 10.14006/j.jzjgxb.2020.0657 ZHANG Sumei, LI Xiaozhong, LU Wei, et al. Experimental study on behavior of steel-tube-confined cfst short columns under axial compression [J]. Journal of Building Structures, 2022, 43(6): 21 − 33. (in Chinese) doi: 10.14006/j.jzjgxb.2020.0657
[33]	Architectural Institute of Japan. Recommendations for design and construction of concrete filled steel tubular structures [S]. Tokyo, Japan: Architectural Institute of Japan, 2008.
[34]	Eurocode 4, Design of composite steel and concrete structures-Part 1-1: General rules and rules for buildings [S]. London: British Standards Institution, 1994.
[35]	ANSI/AISC 360-10−2020, Specification for structural steel buildings [S]. Chicago, USA: American Institute of Steel Construction, 2010.
[36]	CECS 28: 2012, 钢管混凝土结构技术规程[S]. 北京: 中国计划出版社, 2012. CECS 28: 2012, Technical specification for concrete-filled steel tubular structures [S]. Beijing: China Planning Press, 2012. (in Chinese)
[37]	赵均海, 张永强, 李建春, 等. 拉压强度不等材料的厚壁圆筒的统一极限解[J]. 力学与实践, 1999, 21(6): 45 − 47. ZHAO Junhai, ZHANG Yongqiang, LI Jianchun, et al. Unified limit solutions of materials with different tension and compression strengths [J]. Mechanics in Engineering, 1999, 21(6): 45 − 47. (in Chinese)
[38]	罗华. 钢管活性粉末混凝土柱受压性能试验与理论研究[D]. 北京: 北京交通大学, 2015. LUO Hua. Experimental and theoretical study of reactive powder concrete filled steel tube column under compression [D]. Beijing: Beijing Jiaotong University, 2015. (in Chinese)

施引文献(7)

期刊类型引用(3)

1.	李宏男，张鸿志，李庆伟，付兴. FAST馈源舱结构气动力特性及耦联系统风振响应研究. 工程力学. 2025(06): 33-45 . 本站查看
2.	翟露阳，韩佳颖，沈永利. 脉动风作用下船舶风载荷数值仿真. 天津理工大学学报. 2024(03): 17-23 . 百度学术
3.	李波，胡涛，田玉基，刘悦，卢啸，张范，宋晓峰，白凡. 北京2022年冬奥会内场主火炬抗风性能研究. 工程力学. 2024(10): 43-48 . 本站查看

其他类型引用(4)

资源附件(0)

图(10) / 表(8)

计量

文章访问数: 187
HTML全文浏览量: 40
PDF下载量: 50
被引次数: 7

1 试验方案
1.1 试件设计与制作
1.2 材料性能
1.3 试验加载方案及测点布置
2 实验结果与分析
2.1 试验现象与分析
2.2 轴向荷载-位移关系
2.2.1 荷载-位移曲线分类
2.2.2 承载力分析
2.3 轴向荷载-应变关系
2.4 试验结果分析
2.4.1 混凝土贡献率
2.4.2 强度提高系数
3 承载力计算模型
3.1 现行规范对比
3.2 基于设计的承载力计算模型
3.2.1 不锈钢应力
3.2.2 混凝土应力
3.2.3 承载力计算模型
4 结论

1 试验方案
1.1 试件设计与制作
1.2 材料性能
1.3 试验加载方案及测点布置
2 实验结果与分析
2.1 试验现象与分析
2.2 轴向荷载-位移关系
2.2.1 荷载-位移曲线分类
2.2.2 承载力分析
2.3 轴向荷载-应变关系
2.4 试验结果分析
2.4.1 混凝土贡献率
2.4.2 强度提高系数
3 承载力计算模型
3.1 现行规范对比
3.2 基于设计的承载力计算模型
3.2.1 不锈钢应力
3.2.2 混凝土应力
3.2.3 承载力计算模型
4 结论

参考文献(38)

施引文献(7)

资源附件(0)

圆不锈钢管超高性能混凝土短柱轴压性能研究

作者简介: 唐红元(1974−)，男，湖北人，教授，博士，主要从事钢结构及组合结构研究(E-mail: tanghyseu@163.com) 曾跃佳(1997−)，女，四川人，硕士生，主要从事钢结构及组合结构研究(E-mail: 1457959839@qq.com)

通讯作者: 刘 烨(1992−)，男，江苏人，副研究员，博士，主要从事装配式结构抗震和组合结构研究(E-mail: liu.ye@scu.edu.cn)

计量

出版历程

STUDY ON AXIAL-COMPRESSION PERFORMANCE OF CIRCULAR ULTRA-HIGH PERFORMANCE CONCRETE -FILLED SATAINLESS STELL TUBE COLUMN

1 试验方案

1.1 试件设计与制作

1.2 材料性能

1.3 试验加载方案及测点布置

2 实验结果与分析

2.1 试验现象与分析

2.2 轴向荷载-位移关系

2.2.1 荷载-位移曲线分类

2.2.2 承载力分析

2.3 轴向荷载-应变关系

2.4 试验结果分析

2.4.1 混凝土贡献率

2.4.2 强度提高系数

3 承载力计算模型

3.1 现行规范对比

3.2 基于设计的承载力计算模型

3.2.1 不锈钢应力

3.2.2 混凝土应力

3.2.3 承载力计算模型

4 结论

期刊类型引用(3)

其他类型引用(4)

计量

出版历程

目录

1 试验方案

1.1 试件设计与制作

1.2 材料性能

1.3 试验加载方案及测点布置

2 实验结果与分析

2.1 试验现象与分析

2.2 轴向荷载-位移关系

2.2.1 荷载-位移曲线分类

2.2.2 承载力分析

2.3 轴向荷载-应变关系

2.4 试验结果分析

2.4.1 混凝土贡献率

2.4.2 强度提高系数

3 承载力计算模型

3.1 现行规范对比

3.2 基于设计的承载力计算模型

3.2.1 不锈钢应力

3.2.2 混凝土应力

3.2.3 承载力计算模型

4 结论

作者简介:
唐红元(1974−)，男，湖北人，教授，博士，主要从事钢结构及组合结构研究(E-mail: tanghyseu@163.com)

曾跃佳(1997−)，女，四川人，硕士生，主要从事钢结构及组合结构研究(E-mail: 1457959839@qq.com)

通讯作者:
刘　烨(1992−)，男，江苏人，副研究员，博士，主要从事装配式结构抗震和组合结构研究(E-mail: liu.ye@scu.edu.cn)