基于有限质点法的分布协调式多尺度分析

姚俊杰; 郑延丰; 唐敬哲; 汪伟; 杨超; 罗尧治

doi:10.6052/j.issn.1000-4750.2022.11.0958

基于有限质点法的分布协调式多尺度分析

姚俊杰^{1, 2,},
郑延丰^1,,
唐敬哲^1,,
汪伟^1,,
杨超^{1, 3,},
罗尧治^{1, 3, ,}

1.
浙江大学空间结构研究中心，浙江，杭州 310058
2.
浙江大学长三角智慧绿洲创新中心，浙江，嘉兴 314100
3.
浙江省空间结构重点实验室，浙江，杭州 310058

基金项目: 国家自然科学基金项目(52238001，52378203，51908492，52008366)；浙江省自然科学基金项目(LQ21E080019，LY21E080022)

详细信息

作者简介:
姚俊杰(1997−)，男，浙江人，博士生，主要从事空间结构研究(E-mail: junjieyao0817@zju.edu.cn)

郑延丰(1987−)，男，福建人，特聘研究员，博士，主要从事空间结构研究(E-mail: yanfeng39@zju.edu.cn)

唐敬哲(1990−)，男(满族)，陕西人，助理研究员，博士，主要从事空间结构研究(E-mail: tangjingzhe@zju.edu.cn)

汪　伟(1994−)，男，安徽人，博士生，主要从事空间结构研究(E-mail: william_wang@zju.edu.cn)

杨　超(1986−)，男，浙江人，讲师，博士，主要从事空间结构研究(E-mail: 04tmgcyc@zju.edu.cn)

通讯作者:
罗尧治(1966−)，男，浙江人，教授，博士，浙江大学建筑工程学院院长，主要从事空间结构研究(E-mail: luoyz@zju.edu.cn)

中图分类号: TU311.4
计量
- 文章访问数: 235
- HTML全文浏览量: 26
- PDF下载量: 52
出版历程
- 收稿日期: 2022-11-10
- 修回日期: 2023-04-10
- 网络出版日期: 2023-05-11
- 刊出日期: 2025-02-24

COORDINATED DISTRIBUTING MULTI-SCALE ANALYSIS BASED ON FINITE PARTICLE METHOD

YAO Jun-jie^{1, 2,},
ZHENG Yan-feng^1,,
TANG Jing-zhe^1,,
WANG Wei^1,,
YANG Chao^{1, 3,},
LUO Yao-zhi^{1, 3, ,}

1.
Space Structure Research Center of Zhejiang University, Hangzhou, Zhejiang 310058, China
2.
Innovation Center of Yangtze River Delta, Zhejiang University, Jiaxing, Zhejiang 314100, China
3.
Key Laboratory of Space Structures of Zhejiang Province, Hangzhou, Zhejiang 310058, China

摘要

摘要:
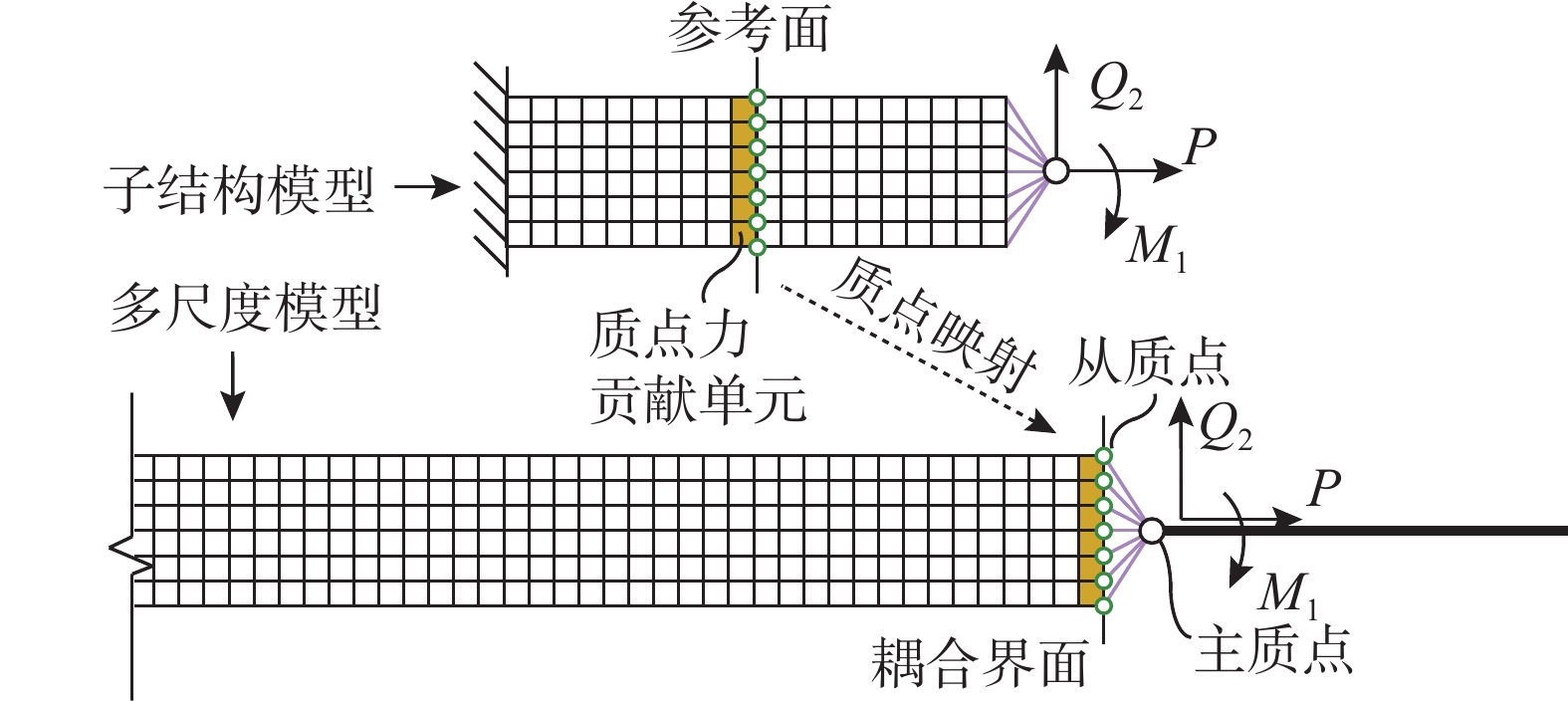
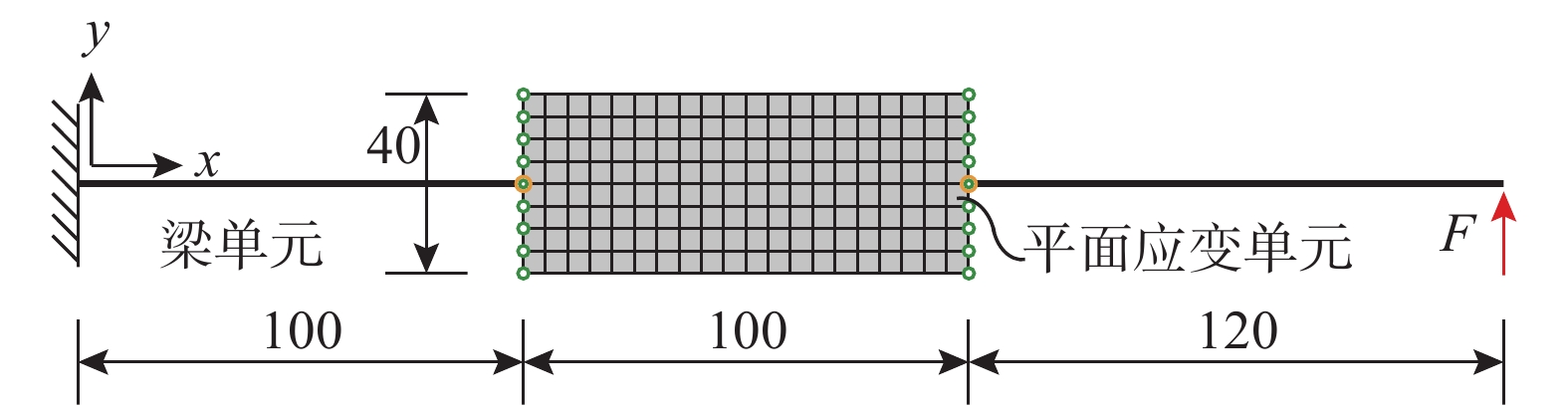
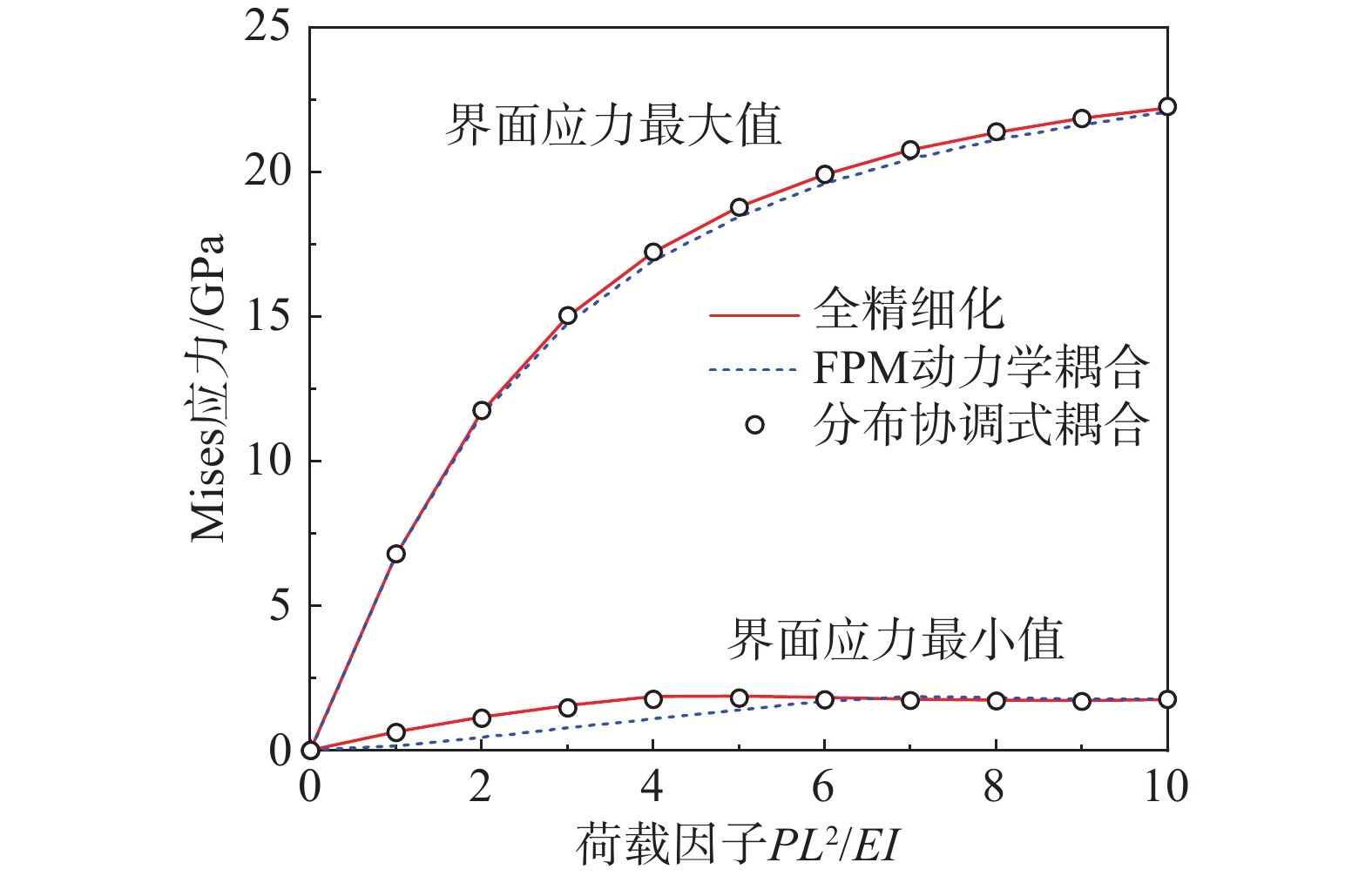
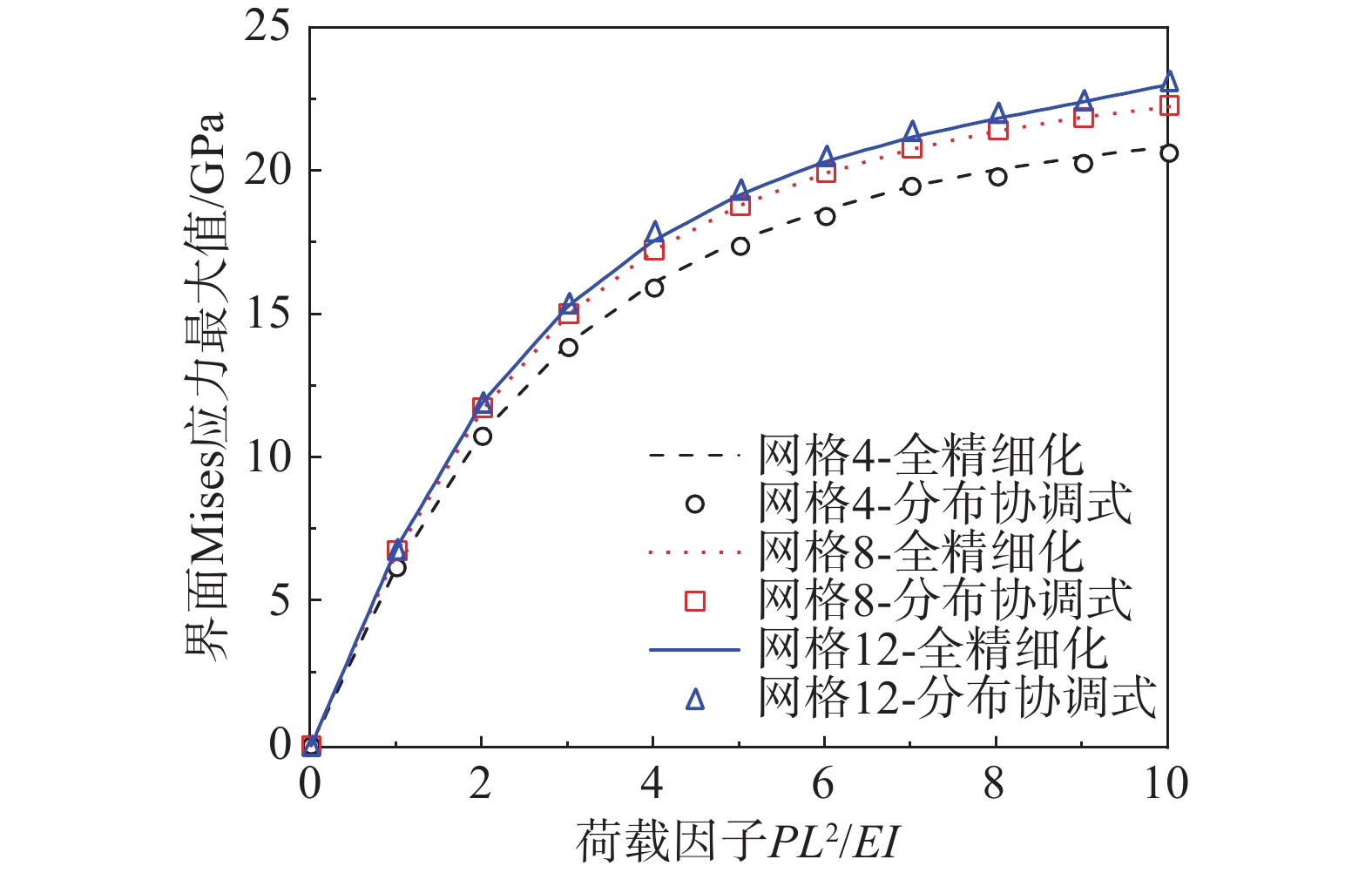
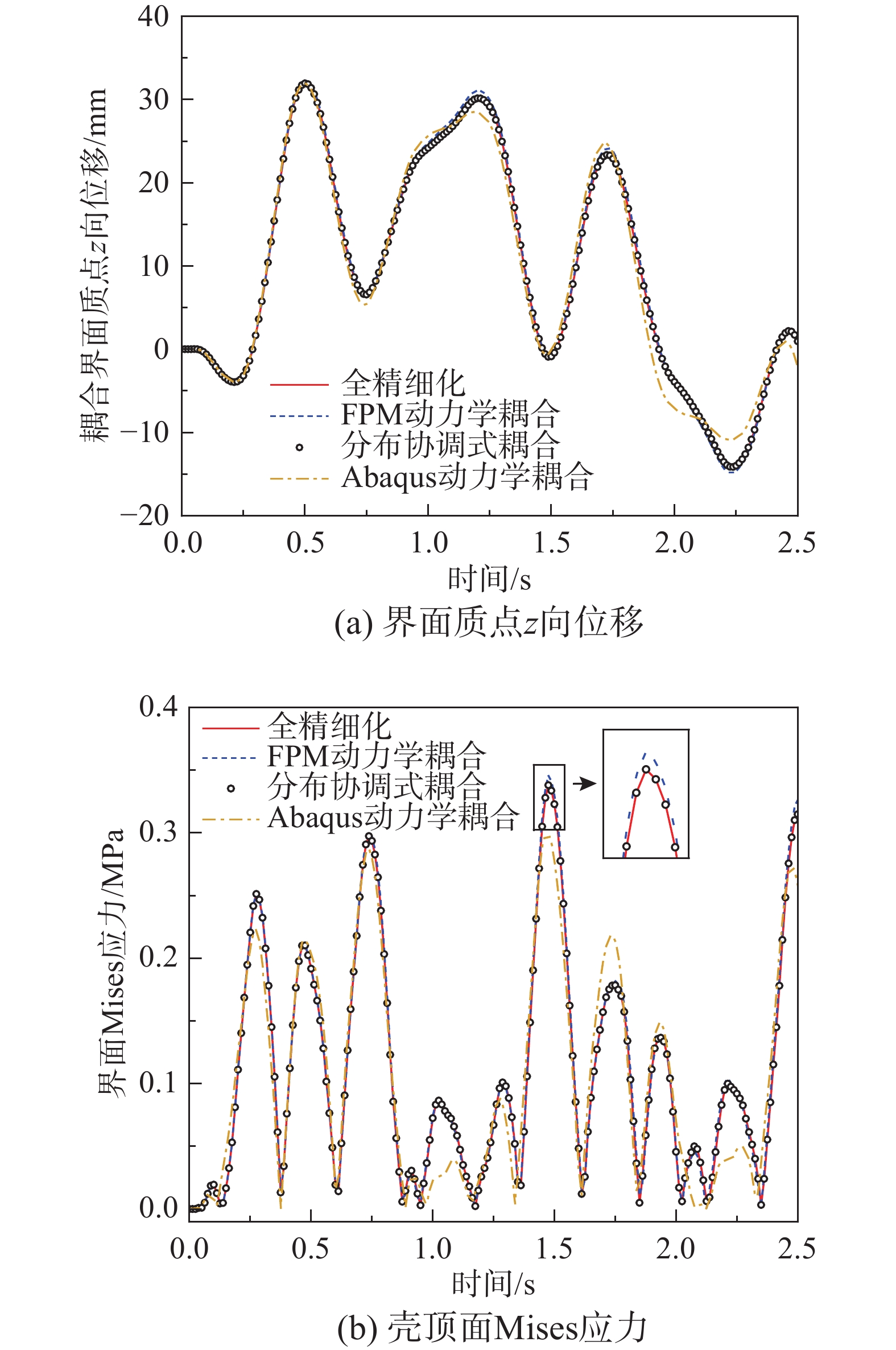
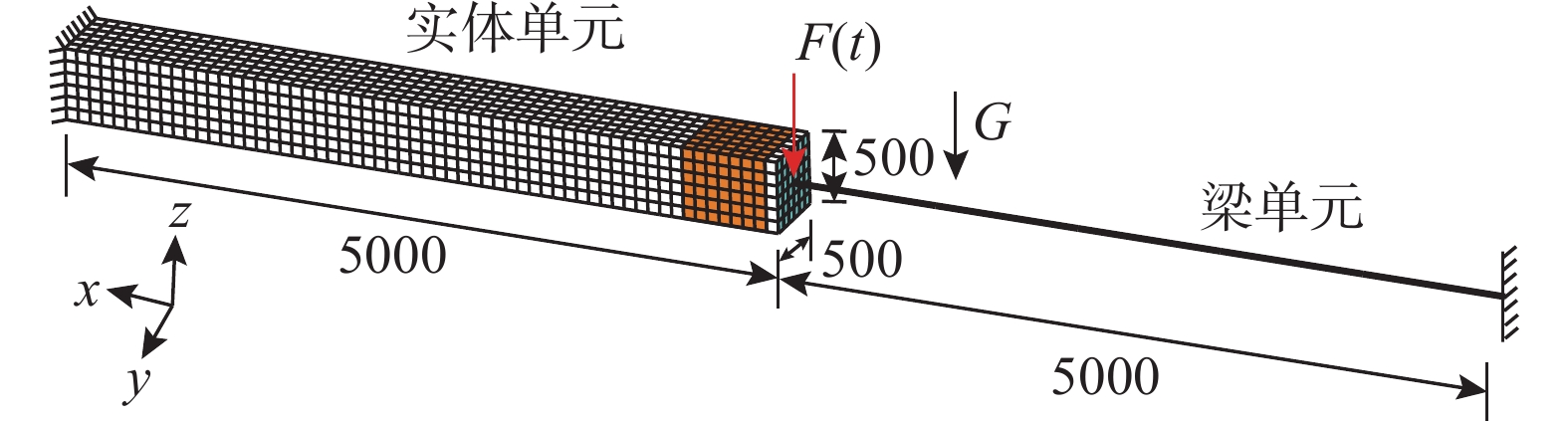
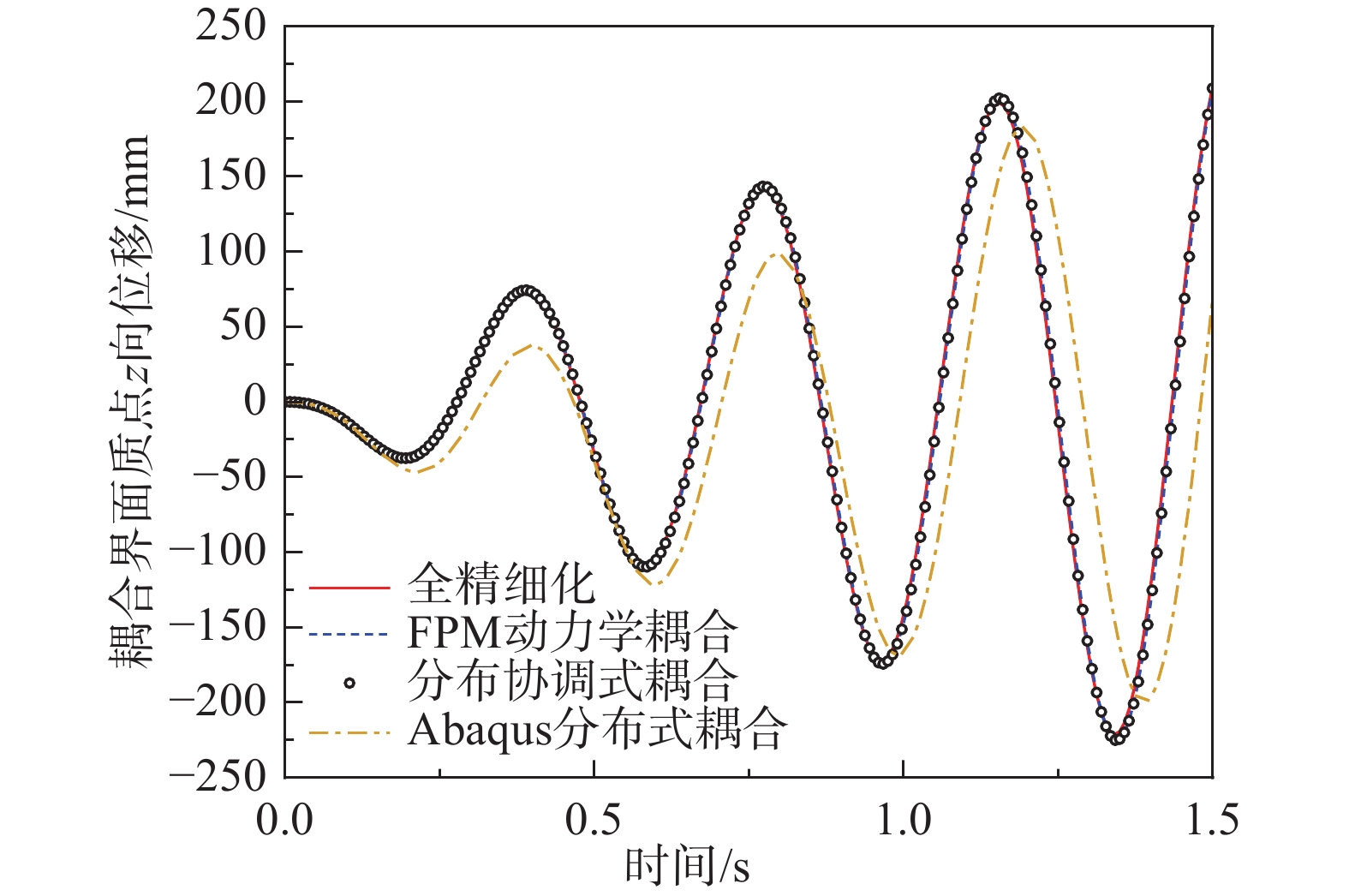
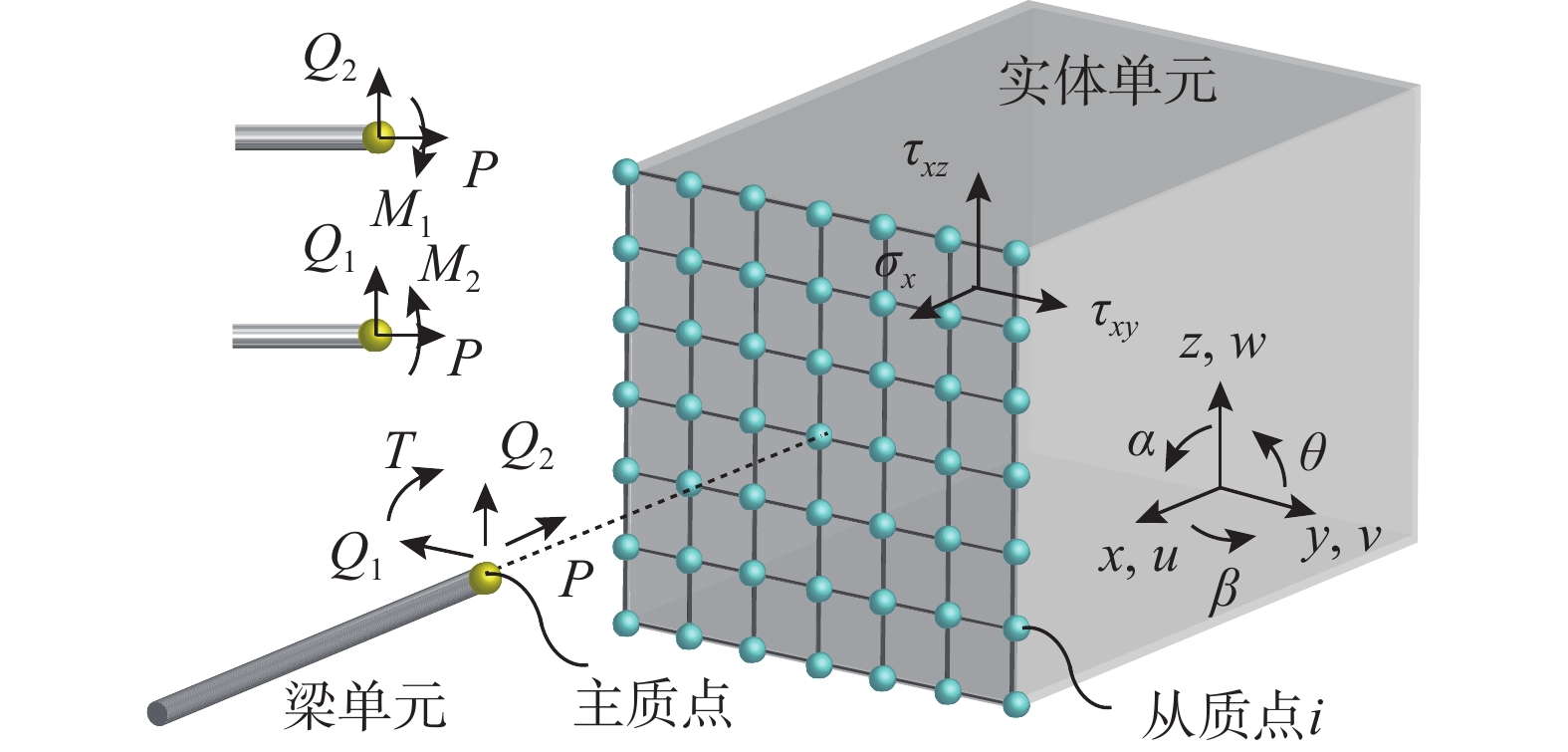
多尺度模型采用“整体宏观，局部精细”的方式来平衡结构数值模拟的计算精度与计算代价，能够在把握结构整体特征的同时获得结构局部信息。该文基于有限质点法点值描述与显式求解的特点，提出了一种考虑界面变形的分布协调式多尺度耦合方法。该文详述了分布协调式多尺度耦合的基本原理，给出了分布协调式多尺度耦合的有限质点法实现流程：计算界面处的作用力，依据力平衡关系将主质点上的界面作用力分配到从质点上，再依据位移协调关系和运动方程求解得到的从质点位移增量来求解主质点的运动。该文实现了梁-平面、梁-壳、梁-实体三种类型的多尺度连接，避免了耦合界面上的应力集中问题，通过算例对比验证了该方法在几何非线性与动力问题中的稳定性与可靠性，为结构多尺度精细化分析提供有效手段。
- 有限质点法 /
- 分布协调式多尺度耦合 /
- 主从质点耦合体系 /
- 位移协调关系 /
- 力平衡关系
Abstract:
Multi-scale modeling is a common method to balance the accuracy and cost of numerical simulation of structures. This method enables designers to obtain both the whole characteristics and local information of structures simultaneously. Based on the Finite Particle Method, a coordinated distributing multi-scale coupling method aiming at deformable interface is proposed in this study. The paper derives the basic theory of coordinated distributing coupling and proposes a calculation process in the following steps. The calculated interface force is distributed to the slave particles according to the force balance relationship. The displacements of the slave particles are obtained through the motion equation. The motion of the master particle is calculated by applying the displacement coordination relationship. This method has realized the beam-plane, beam-shell and beam-solid coupling while avoiding stress concentration at the interface. Numerical tests have been conducted to validate its stability and reliability in dynamic nonlinear problems. The calculation results indicate that the method is effective for multi-scale fine analysis of structures.

HTML全文

图 1 梁-六面体实体的主从质点耦合体系

Figure 1. Master-slave particle coupling system of beam-hexahedral solid

下载: 全尺寸图片幻灯片

图 2 子结构及参考面示意图

Figure 2. Substructure and reference plane

下载: 全尺寸图片幻灯片

图 3 分布协调式耦合算法的整体流程图

Figure 3. Process of coordinated distributing coupling algorithm

下载: 全尺寸图片幻灯片

图 4 梁-平面单元耦合：几何示意图　/mm

Figure 4. Coupling for beam-plane: geometric schematic

下载: 全尺寸图片幻灯片

图 5 梁-平面单元耦合：小变形下平面单元切应力分布

Figure 5. Coupling for beam-plane: shear stress distribution of plane element under small deformation

下载: 全尺寸图片幻灯片

图 6 梁-平面单元耦合：大变形下平面单元Mises应力分布

Figure 6. Coupling for beam-plane: Mises stress distribution of plane element under large deformation

下载: 全尺寸图片幻灯片

图 7 梁-平面单元耦合：大变形下界面Mises应力最值-荷载因子曲线

Figure 7. Coupling for beam-plane: Mises stress maximum-load factor curve at the interface under large deformation

下载: 全尺寸图片幻灯片

图 8 梁-平面单元耦合：不同网格密度界面Mises应力最大值-荷载因子曲线

Figure 8. Coupling for beam-plane: Mises stress maximum-load factor curve at the interface in different mesh densities

下载: 全尺寸图片幻灯片

图 9 梁-平面单元耦合：计算耗时对比曲线

Figure 9. Coupling for beam-plane: Calculation time comparison curve

下载: 全尺寸图片幻灯片

图 10 梁-壳耦合：几何示意图　/mm

Figure 10. Coupling for beam-shell: geometric schematic

下载: 全尺寸图片幻灯片

图 11 梁-壳耦合：自由端荷载位移曲线

Figure 11. Coupling for beam-shell: load displacement curve at the free end

下载: 全尺寸图片幻灯片

图 12 梁-壳耦合：时程荷载下界面质点z向位移曲线和界面Mises曲线

Figure 12. Coupling for beam-shell: z displacement and Mises stress curve at the interface particle under time history load

下载: 全尺寸图片幻灯片

图 13 梁-实体耦合(受弯)：几何示意图　/mm

Figure 13. Coupling for beam-solid (bending): schematic

下载: 全尺寸图片幻灯片

图 14 梁-实体耦合(受弯)：重力下界面处单元切应力分布

Figure 14. Coupling for beam-solid (bending): shear stress distribution at the interface under gravity

下载: 全尺寸图片幻灯片

图 15 梁-实体耦合(受弯)：时程荷载下界面质点z向位移曲线

Figure 15. Coupling for beam-solid (bending): z displacement curve at the interface particle under time history load

下载: 全尺寸图片幻灯片

图 16 梁-实体耦合(受弯)：时程荷载下界面切应力曲线

Figure 16. Coupling for beam-solid (bending): Shear stress curve at the interface under time history load

下载: 全尺寸图片幻灯片

图 17 梁-实体耦合(受扭)：几何示意图　/mm

Figure 17. Coupling for beam-solid (torsion): schematic

下载: 全尺寸图片幻灯片

图 18 梁-实体耦合(受扭)：界面处单元Mises应力分布

Figure 18. Coupling for beam-solid (torsion): Mises stress distribution at the interface

下载: 全尺寸图片幻灯片

图 19 梁-实体耦合(复杂受力)：界面处单元Mises应力分布

Figure 19. Coupling for beam-solid (complicated loading states): Mises stress distribution at the interface

下载: 全尺寸图片幻灯片

参考文献(26)

[1]	SHIM K W, MONAGHAN D J, ARMSTRONG C G. Mixed dimensional coupling in finite element stress analysis [J]. Engineering with Computers, 2002, 18(3): 241 − 252. doi: 10.1007/s003660200021
[2]	LU W, CUI Y, TENG J. Mixed-dimensional coupling method for box section member based on the optimal stress distribution pattern [J]. Measurement, 2019, 131: 277 − 287. doi: 10.1016/j.measurement.2018.08.060
[3]	张雨笛, 程小卫, 李易, 等. FRP布加固混凝土框架子结构抗连续倒塌的精细有限元分析[J]. 工程力学, 2022, 39(12): 151 − 164. doi: 10.6052/j.issn.1000-4750.2021.07.0549 ZHANG Yudi, CHENG Xiaowei, LI Yi, et al. A detailed numerical analysis for the progressive collapse of concrete frame substructures strengthened with frp strips [J]. Engineering Mechanics, 2022, 39(12): 151 − 164. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.07.0549
[4]	DING Y L, LI A Q, DU D S, et al. Multi-scale damage analysis for a steel box girder of a long-span cable-stayed bridge [J]. Structure and Infrastructure Engineering, 2010, 6(6): 725 − 739. doi: 10.1080/15732470802187680
[5]	MATA P, BARBAT A H, OLLER S. Two-scale approach for the nonlinear dynamic analysis of RC structures with local non-prismatic parts [J]. Engineering Structures, 2008, 30(12): 3667 − 3680. doi: 10.1016/j.engstruct.2008.06.011
[6]	TING E C, SHIH C, WANG Y K. Fundamentals of a vector form intrinsic finite element: Part I. Basic procedure and a plane frame element [J]. Journal of Mechanics, 2004, 20(2): 113 − 122. doi: 10.1017/S1727719100003336
[7]	TING E C, SHIH C, WANG Y K. Fundamentals of a vector form intrinsic finite element: Part II. Plane solid elements [J]. Journal of Mechanics, 2004, 20(2): 123 − 132. doi: 10.1017/S1727719100003348
[8]	SHIH C, WANG Y K, TING E C. Fundamentals of a vector form intrinsic finite element: Part III. Convected material frame and examples [J]. Journal of Mechanics, 2004, 20(2): 133 − 143. doi: 10.1017/S172771910000335X
[9]	罗尧治, 郑延丰, 杨超, 等. 结构复杂行为分析的有限质点法研究综述[J]. 工程力学, 2014, 31(8): 1 − 7, 23. doi: 10.6052/j.issn.1000-4750.2013.05.ST14 LUO Yaozhi, ZHENG Yanfeng, YANG Chao, et al. Review of the finite particle method for complex behaviors of structures [J]. Engineering Mechanics, 2014, 31(8): 1 − 7, 23. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.05.ST14
[10]	喻莹, 许贤, 罗尧治. 基于有限质点法的结构动力非线性行为分析[J]. 工程力学, 2012, 29(6): 63 − 69, 84. doi: 10.6052/j.issn.1000-4750.2010.08.0746 YU Ying, XU Xian, LUO Yaozhi. Dynamic nonlinear analysis of structures based on the finite particle method [J]. Engineering Mechanics, 2012, 29(6): 63 − 69, 84. (in Chinese) doi: 10.6052/j.issn.1000-4750.2010.08.0746
[11]	林贤宏, 罗尧治, 唐敬哲, 等. 考虑剪切和扭转变形的有限质点法纤维梁单元研究[J]. 工程力学, 2022, 39(5): 34 − 43. doi: 10.6052/j.issn.1000-4750.2021.03.0184 LIN Xianhong, LUO Yaozhi, TANG Jingzhe, et al. A fiber beam element for the finite particle method considering shear and torsion deformation [J]. Engineering Mechanics, 2022, 39(5): 34 − 43. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.03.0184
[12]	喻莹, 罗尧治. 基于有限质点法的结构倒塌破坏研究Ⅰ: 基本方法[J]. 建筑结构学报, 2011, 32(11): 17 − 26. YU Ying, LUO Yaozhi. Structural collapse analysis based on finite particle method I: Basic approach [J]. Journal of Building Structures, 2011, 32(11): 17 − 26. (in Chinese)
[13]	唐敬哲, 汪伟, 郑延丰, 等. 基于并行有限质点法的界面断裂-接触行为分析[J]. 工程力学, 2021, 38(6): 24 − 35. doi: 10.6052/j.issn.1000-4750.2020.06.0424 TANG Jingzhe, WANG Wei, ZHENG Yanfeng, at el. Interface failure and contact analysis based on parallelized finite particle method [J]. Engineering Mechanics, 2021, 38(6): 24 − 35. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0424
[14]	郑延丰, 杨超, 刘磊, 等. 基于有限质点法的含间隙铰平面机构动力分析[J]. 工程力学, 2020, 37(3): 8 − 17. doi: 10.6052/j.issn.1000-4750.2019.04.0212 ZHENG Yanfeng, YANG Chao, LIU Lei, et al. Dynamics analysis of planar mechanism with revolute joint clearance based on finite particle method [J]. Engineering Mechanics, 2020, 37(3): 8 − 17. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.0212
[15]	WANG W, ZHENG Y F, TANG J Z, et al. A GPU-based parallel algorithm for 2D large deformation contact problems using the finite particle method [J]. Computer Modeling in Engineering & Sciences, 2021, 129(2): 595 − 626.
[16]	张鹏飞, 罗尧治, 杨超. 薄壳屈曲问题的有限质点法求解[J]. 工程力学, 2017, 34(2): 12 − 20. doi: 10.6052/j.issn.1000-4750.2015.07.0623 ZHANG Pengfei, LUO Yaozhi, YANG Chao. Buckling analysis of thin shell using the finite particle method [J]. Engineering Mechanics, 2017, 34(2): 12 − 20. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.07.0623
[17]	杨超, 罗尧治, 郑延丰. 正交异性膜材大变形行为的有限质点法求解[J]. 工程力学, 2019, 36(7): 18 − 29. doi: 10.6052/j.issn.1000-4750.2018.06.0318 YANG Chao, LUO Yaozhi, ZHENG Yanfeng. Large deformation analysis of orthotropic membranes using the finite particle method [J]. Engineering Mechanics, 2019, 36(7): 18 − 29. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.06.0318
[18]	TANG J Z, ZHENG Y F, YANG C, et al. Parallelized implementation of the finite particle method for explicit dynamics in GPU [J]. Computer Modeling in Engineering & Sciences, 2020, 122(1): 5 − 31.
[19]	BOURNIVAL S, CUILLIÈRE J C, FRANÇOIS V. A mesh-geometry based method for coupling 1D and 3D elements [J]. Advances in Engineering Software, 2010, 41(6): 838 − 858. doi: 10.1016/j.advengsoft.2010.02.004
[20]	ZHENG Z Y, LI Z X, CHEN Z W. Adaptive multiscale analyses on structural failure considering localized damage evolution on vulnerable joints [J]. Archives of Civil and Mechanical Engineering, 2014, 14(2): 304 − 316. doi: 10.1016/j.acme.2013.08.004
[21]	WANG F Y, XU Y L, QU W L. Mixed-dimensional finite element coupling for structural multi-scale simulation [J]. Finite Elements in Analysis and Design, 2014, 92: 12 − 25. doi: 10.1016/j.finel.2014.07.009
[22]	MCCUNE R W, ARMSTRONG C G, ROBINSON D J. Mixed-dimensional coupling in finite element models [J]. International Journal for Numerical Methods in Engineering, 2000, 49(6): 725 − 750. doi: 10.1002/1097-0207(20001030)49:6<725::AID-NME967>3.0.CO;2-W
[23]	YAN F, CHEN W Z, LIN Z B. Prediction of fatigue life of welded details in cable-stayed orthotropic steel deck bridges [J]. Engineering Structures, 2016, 127: 344 − 358. doi: 10.1016/j.engstruct.2016.08.055
[24]	HO R J, MEGUID S A, ZHU Z H, et al. Consistent element coupling in nonlinear static and dynamic analyses using explicit solvers [J]. International Journal of Mechanics and Materials in Design, 2010, 6(4): 319 − 330. doi: 10.1007/s10999-010-9139-x
[25]	郑延丰, 罗尧治. 基于有限质点法的多尺度精细化分析[J]. 工程力学, 2016, 33(9): 21 − 29. doi: 10.6052/j.issn.1000-4750.2015.02.0144 ZHENG Yanfeng, LUO Yaozhi. Multi-scale fine analysis based on the finite particle method [J]. Engineering Mechanics, 2016, 33(9): 21 − 29. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.02.0144
[26]	KO Y, LEE P S, BATHE K J. A new MITC4+ shell element [J]. Computers & Structures, 2017, 182: 404 − 418.