MODEL UPDATING OF A LONG-SPAN BRIDGE BASED ON AN OPEN-SOURCE PROGRAM
-
摘要:
大跨桥梁作为重要的基础工程设施，准确评估其即时服役状态、建立高保真数值模型是提升城市交通防灾水平的重要途径，实现上述目标依赖于高效可靠的复杂结构模型更新与分析技术。但已有研究多依赖商业软件平台，存在价格昂贵、算法更新速度较慢和软件接口复杂等局限性，限制了相关研究的深入发展。因此，该文基于开源有限元分析平台OpenSees和编程语言Python，开发了适用于复杂工程结构模型更新的开源程序框架。基于Python开发了工程结构模型更新所需的高效并行优化算法，进一步编写不同功能模块的软件接口，连接模型分析平台与并行优化算法，实现复杂工程结构模型的并行分析和模型更新。在此基础上，以一个简支梁损伤识别为例，验证了上述计算程序的有效性与计算精度。以苏通大桥振动台试验缩尺模型为研究对象，采用模态置信准则匹配有限元模型和振动台试验获得的模态振型和频率数据，构建模型更新所需的优化函数，采用高性能计算平台，开展试验桥梁的模型更新并验证上述程序框架的计算效率。结果表明，该框架可以实现大跨斜拉桥精细有限元模型的高效更新，匹配实测获得的结构模态数据，各阶计算频率与试验模型的误差在1%以下。进一步地，计算更新后的数值模型在PGA=0.1 g地震动作用下的动力时程响应，与试验数据对比验证了模型更新结果的准确性。研究成果可以为基于开源平台的复杂大跨桥梁的精细化与数据驱动建模提供参考。
Abstract:Long-span bridges often serve as critical infrastructures. It is therefore important to accurately assess the immediate structural performance and build high-fidelity finite element (FE) models of these bridges to improve the disaster prevention capacity of urban transportation. Achieving the above goals relies on efficient and reliable model updating and analysis techniques suitable for complex structures. However, most of the previous studies were based on commercial software platforms, which were expensive, slowly updated and had complicated application programming interfaces, and thus limited the development of further in-depth research. Based on the open-source software OpenSees and Python, a program framework suitable for the model updating of complex structures was proposed. An efficient parallel optimization algorithm for FE model updating (FEMU) of complex civil structures was developed in Python. The program interfaces were developed to link the model analysis module and the parallel computing module to realize the parallel analysis and FEMU of complex structures. On this basis, the damage identification of a simply-supported beam was taken as an example to validate the feasibility and accuracy of the program framework. Further, the scaled physical model of Sutong cable-stayed bridge in a shake table test was selected as the object. The modal assurance criterion (MAC) was used to match the simulated modal shapes and frequencies with those identified from the shake table test to form the objective function for the FEMU. The FEMU of the bridge was carried out on a high-performance computing platform to validate the computational efficiency of the program framework. The results show that the framework can effectively tune the high-fidelity FE model of the long-span cable-stayed bridge to match up with the experimental measurement. The error between the simulated frequencies and the physical model was below 1%. Furthermore, the accuracy of the updated model was verified by comparing the measured responses with the predicted ones using the updated FE models under the seismic input with a PGA of 0.1 g. The research outcome can provide references for high-fidelity and data-driven modeling of complex long-span bridges based on open-source platforms.
-
大跨桥梁作为重要的交通工程生命线，其设计使用寿命往往在百年以上。但在服役期间，桥梁受到风、地震、波浪和车辆荷载等的长期作用而发生结构损伤和性能退化，使得结构无法达到预期设计的使用年限，存在较大的风险[1]。由于根据设计资料建立的数值模型往往存在大量建模假定等，无法准确预测和模拟结构中潜在的损伤，因此，大量学者通过模型更新将监测系统获得的实测数据映射到数值模型上，以模拟在役桥梁的服役性能[2]。
既有模型更新多通过选取结构物理参数(几何尺寸、材料特性等)作为优化变量，根据响应数据类型构建合适的目标函数从而将模型参数修正转化为多目标优化问题，通过智能优化算法[3-4]迭代调整模型参数，优化目标函数取值，使数值模型响应和结构现场实测数据相匹配。如ZHU等[5]建立香港昂船洲大桥的多尺度模型，根据模态信息和影响线的实测数据，基于响应面法和多起点的梯度算法更新了桥梁的有限元模型，并与实测结果进行了对比验证；TRAN-NGOC等[6]基于MATLAB工具箱StaBil建立了一座主跨75 m的下承式钢桁架拱桥的简化模型，通过遗传算法和粒子群算法实现模型更新，研究了不同钢节点简化模型对服役性能的影响。
大跨桥梁往往会安装大量传感器，可以获得丰富的监测数据，但是由于构造复杂、自由度大和更新参数多等问题，其数值模型计算耗时长，更新过程需要消耗巨大计算资源。既有研究中多采用代理模型(如响应面法[7]和Kriging模型[8])或贝叶斯理论开展相关研究。然而，尽管采用代理模型替代初始复杂模型开展模型更新可以有效降低模型复杂度，加速更新过程，但其存在精度较低，多适用于线性工况等局限性[9]，难以准确映射大跨桥梁可能存在的复杂损伤状态。同时，建立代理模型的过程也需要大量基于初始模型的计算数据，而贝叶斯理论[10]等概率统计方法往往依赖样本数据的大小，也多针对线弹性响应数据，较少应用于非线性模型更新。因此，亟需开发适用于大跨桥梁精细数值模型的高效模型更新程序框架。
随着计算机技术的发展，利用云计算和集群计算等新兴技术可以有效加速复杂结构的精细模型更新，为建立大跨桥梁的数字孪生提供了技术基础。例如，LIN等[11]基于MSC.Marc和MATLAB开发了适用于大跨斜拉桥线性和非线性模型更新的集群计算程序。但是，既有研究多基于商用软件，配套软件价格昂贵且难以形成自主知识产权。此外，复杂结构的模型更新往往依赖高效的智能优化算法，如遗传算法[11-12]、粒子群算法[13-14]等，而商用软件平台的算法集成、更新换代极度依赖软件发行商。相比而言，Python和OpenSees作为开源的高级程序设计语言和数值分析软件，具备更自由的软件开发权限、更全面的科学计算函数库和更短的算法/功能迭代周期，有助于程序的快速推广和相关研究领域的发展。
基于上述需求，本文基于开源平台Python和OpenSees开发了适用于复杂大跨桥梁精细模型更新的并行程序框架。在此基础上，分别以一个简支梁及苏通大桥振动台试验为例，验证了上述程序框架开展结构损伤识别和复杂结构模型更新的可靠性和计算精度。
1 程序平台
1.1 有限元计算平台——OpenSees
本文采用的开源有限元计算平台为OpenSees，其具备强大的线性、非线性分析能力和二次开发可拓展性。许多学者基于OpenSees开展了复杂结构(如超高层建筑[15-16]，大跨斜拉桥[17]等)的精细有限元模拟工作。
1.2 并行分析和智能优化计算平台——Python
除了模型分析软件外，由于复杂结构的模型更新在匹配实测数据并迭代优化建模参数过程中，会消耗大量的计算资源，因此需要开发相应的高性能并行分析框架和智能优化算法。
在并行分析方面，Python为面向CPU密集型和I/O(Input/Output)密集型任务提供了开源的并行计算库[18]，可以实现多任务的并行以加速计算任务；在优化算法方面，本文对群体智能算法库scikit-opt[19]进行二次开发，使其可以实现复杂结构的有限元模型更新。
2 程序框架
复杂结构的有限元模型更新一般包含3个主要部分[11]：1)目标函数；2)更新参数；3)优化算法。其中，更新参数需要依据结构模型的实际情况确定，下面主要介绍本文模型更新程序框架中的目标函数和优化算法。
2.1 目标函数
目标函数通常用于量化实际结构和数值模型之间特征数据的差异。特征数据可以直接采用试验量测的数据[20]或者实测数据后处理所获得的结构固有特性，如周期、模态、阻尼比[2]等。在模型更新过程中，通过迭代、修正更新参数以不断优化目标函数值，实现模型更新。
由于本文旨在开发基于并行计算的开源模型更新框架，因此参考既有研究，算例中采用常用的结构自振频率的最小二乘误差为目标函数，如式(1)所示：
{\rm{OBJ}}({\boldsymbol{x}}) = \sum\limits_{i = 1}^n {{{[ {( {{f_i}({\boldsymbol{x}}) - {f_{i,\exp }}} )/{f_{i,\exp }}} ]}^2}} (1) 式中：x为更新参数向量；fi,exp和fi(x)分别为根据测量数据识别出的第i个结构自振频率和对应的有限元模拟结果；n为目标函数中参与计算的模态数量。采用模态置信准则[21](Modal Assurance Criterion, MAC)匹配数值模拟和实测的模态振型，如式(2)所示：
{\rm{MAC}} = \frac{{{{| {{{\{ {{{\boldsymbol{\phi}} _{{\text{FE}}}}} \}}^{\text{T}}}\{ {{{\boldsymbol{\phi}} _{\exp }}} \}} |}^2}}}{{( {{{\{ {{{\boldsymbol{\phi}} _{{\text{FE}}}}} \}}^{\text{T}}}\{ {{{\boldsymbol{\phi}} _{{\text{FE}}}}} \}} )( {{{\{ {{{\boldsymbol{\phi}} _{\exp }}} \}}^{\text{T}}}\{ {{{\boldsymbol{\phi}} _{\exp }}} \}} )}} (2) 式中，{{\boldsymbol{\phi}} exp}和{{\boldsymbol{\phi}} FE}分别为数值模型计算和实际工程中识别的振型矩阵。MAC为标量，值在0~1之间，数值越大，模态一致性越高。在其他实际案例的应用中，可以根据实测数据情况修改目标函数形式。
2.2 优化算法
在模型更新过程中，优化算法主要用于迭代更新模型参数以优化目标函数值。相比于传统的梯度优化算法，既有研究表明启发式全局优化算法更适用于复杂结构的模型更新[22]。其中，scikit-opt算法库中就封装了包括遗传算法(Genetic Algorithm, GA)和粒子群优化算法(Particle Swarm Optimization, PSO)等多种启发式全局优化算法。为了说明本平台在算法开发方面的优势，本文对scikit-opt中的GA和PSO算法进行了二次开发并对比了其计算精度和效率。首先，以PSO算法为例来说明全局优化算法在模型更新的工作原理。
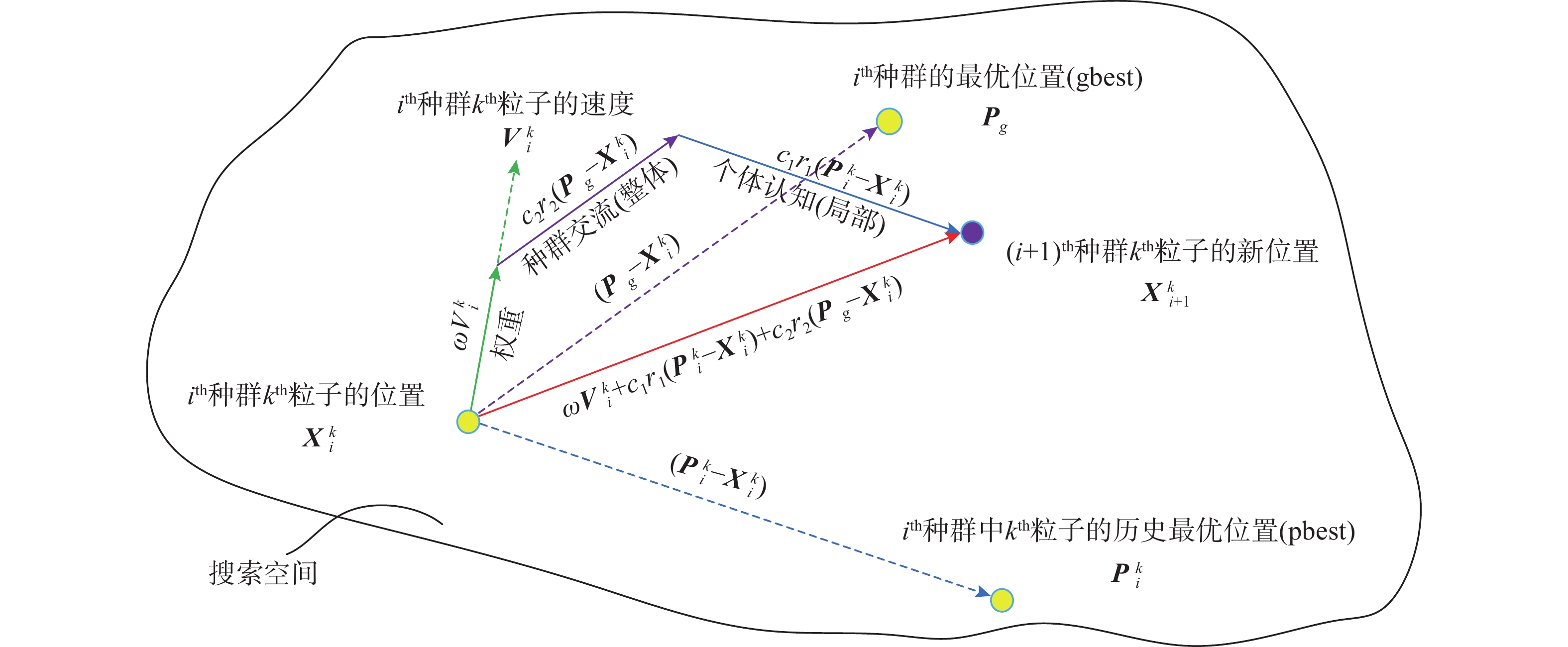
PSO算法由KENNEDY和EBERHART[23]提出，其原理为在搜索空间中随机生成一定数量的粒子群，每一个粒子由n个更新参数组成的n维向量表示，对应其在搜索空间中的位置，如图1所示。在本文中，每个粒子对应的n维更新参数向量通过转换为对应有限元模型，运行分析并计算得到对应的目标函数值，作为不同粒子的适应度。迭代过程中，根据粒子的适应度对每一代粒子群进行筛选、迭代，逐步接近目标函数的最优值。
在每一代的粒子群中，不同粒子的适应度计算是相互独立的，因此可以将粒子的计算任务分配给不同的物理核心(CPU)上的线程并行计算以实现算法加速，本文采用Python中的multiprocessing模块来分布计算任务和收集计算结果。
2.3 程序框架实现
为了实现复杂结构的模型更新及其并行加速，本文基于Python编写了Input.py、Parallel.py及Optimization.py三个程序模块，不同模块间的数据传递、相互关系及部分关键代码如图2所示，其中：1) Input.py用于定义算法参数、归一化参数的上下限和设置并行计算环境；2) Optimization.py主要依次通过三个函数Modify_tcl( )、Run_OpenSees( )、Objective_function( )来分别实现结构模型的参数修正、计算分析和目标函数值计算；3) Parallel.py用于调用multiprocessing模块创建并行计算所需的进程池以实现优化算法的并行计算。其中，进程池里的每个进程分别独立调用Optimization.py来计算每个更新参数向量的目标函数。在此基础上，PSO算法根据各粒子的目标函数值生成下一代更新参数向量集合(粒子群)，实现复杂模型的迭代更新。
![]()
图 2 程序框架的实现流程和部分关键代码Figure 2. The flowchart and key code fragments of the program framework此外，在分析过程中，上述程序框架通过读取进程池中每一个进程的进程号和进程开始时间创建更新过程文件，以解决由于多线程并行优化可能导致的程序占用而无法外部访问的问题，并记录迭代过程中的更新参数向量及其对应的目标函数值。上述程序的相关代码和典型算例已开源在GitHub[24]。
3 算例验证
既有研究表明，模型更新可以用于结构的损伤识别、模型参数修正等领域[2]，因此，本文分别以一个损伤简支梁和苏通大桥振动台试验为例，验证上述程序框架应用于结构损伤识别和模型更新的可行性和计算精度。
3.1 算例1-结构损伤识别
3.1.1 损伤简支梁模型
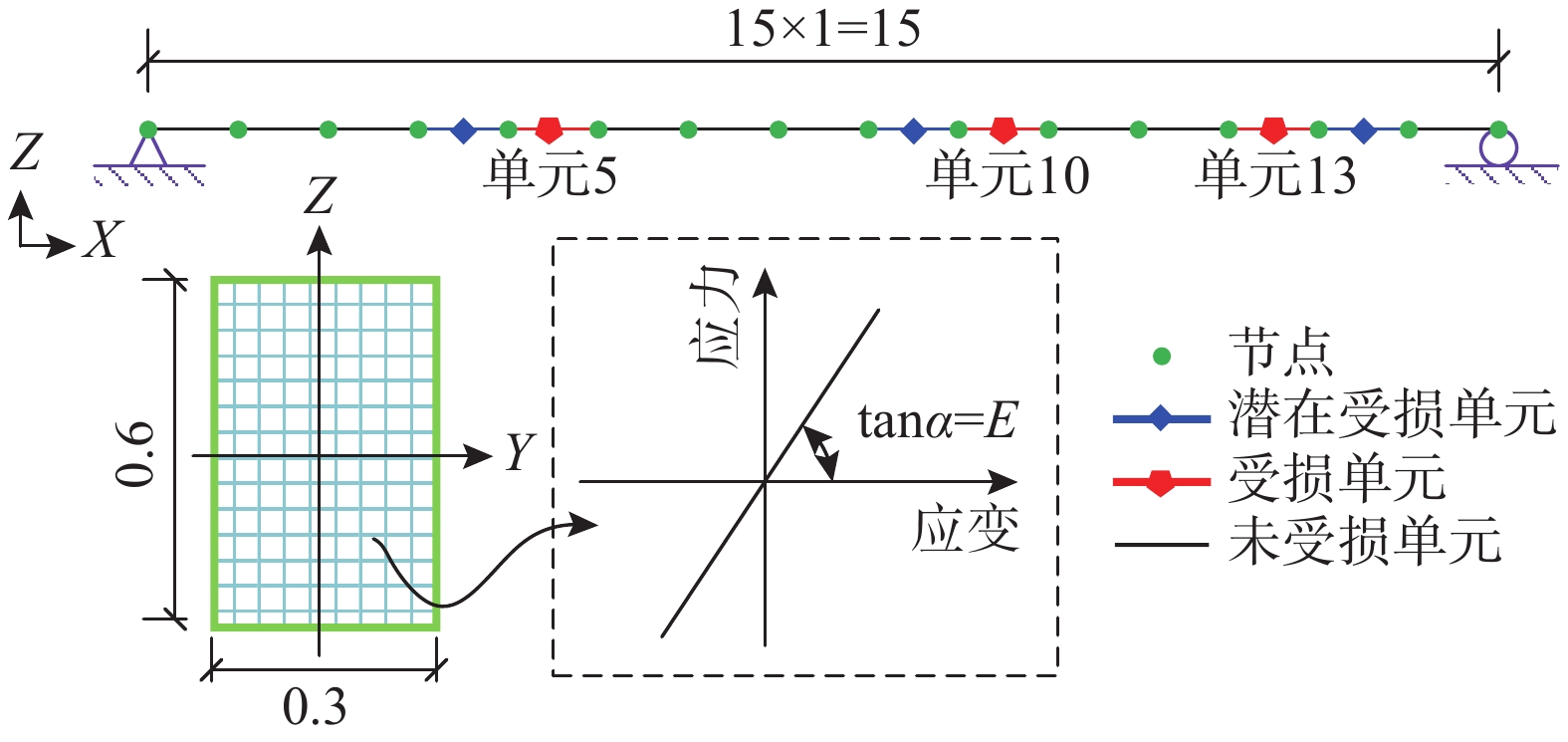
本节选用的简支梁跨度为15 m，其截面尺寸为0.6 m×0.3 m，材料弹性模量取3.45×104 MPa，泊松比为0.3，材料密度取2500 kg/m3，更新算法采用PSO算法。首先，采用OpenSees的梁单元建立简支梁的有限元模型，模型沿梁长划分为15个单元，如图3所示。
参考万华平等[25]的研究，通过降低部分单元的刚度以模拟简支梁局部损伤。具体地，假定上述简支梁在单元5、单元10和单元13位置处存在损伤，将相应单元的截面惯性矩降为原来的30%，其余特性保持不变。
基于上述模型，首先开展“损伤”模型的模态分析，提取前10阶自振频率及Y/Z方向振型向量，作为“实测”数据用于构造目标函数。既有研究表明，可以采用曲率模态测量[26]、小波分析[27]等方法估计结构损伤的大致位置。因此，本算例假设4号、5号、9号、10号、14号和13号单元可能发生损伤，由上述6个单元的截面惯性矩折减系数组成更新参数向量，采用所提出的程序框架开展简支梁的损伤识别。
3.1.2 损伤识别结果
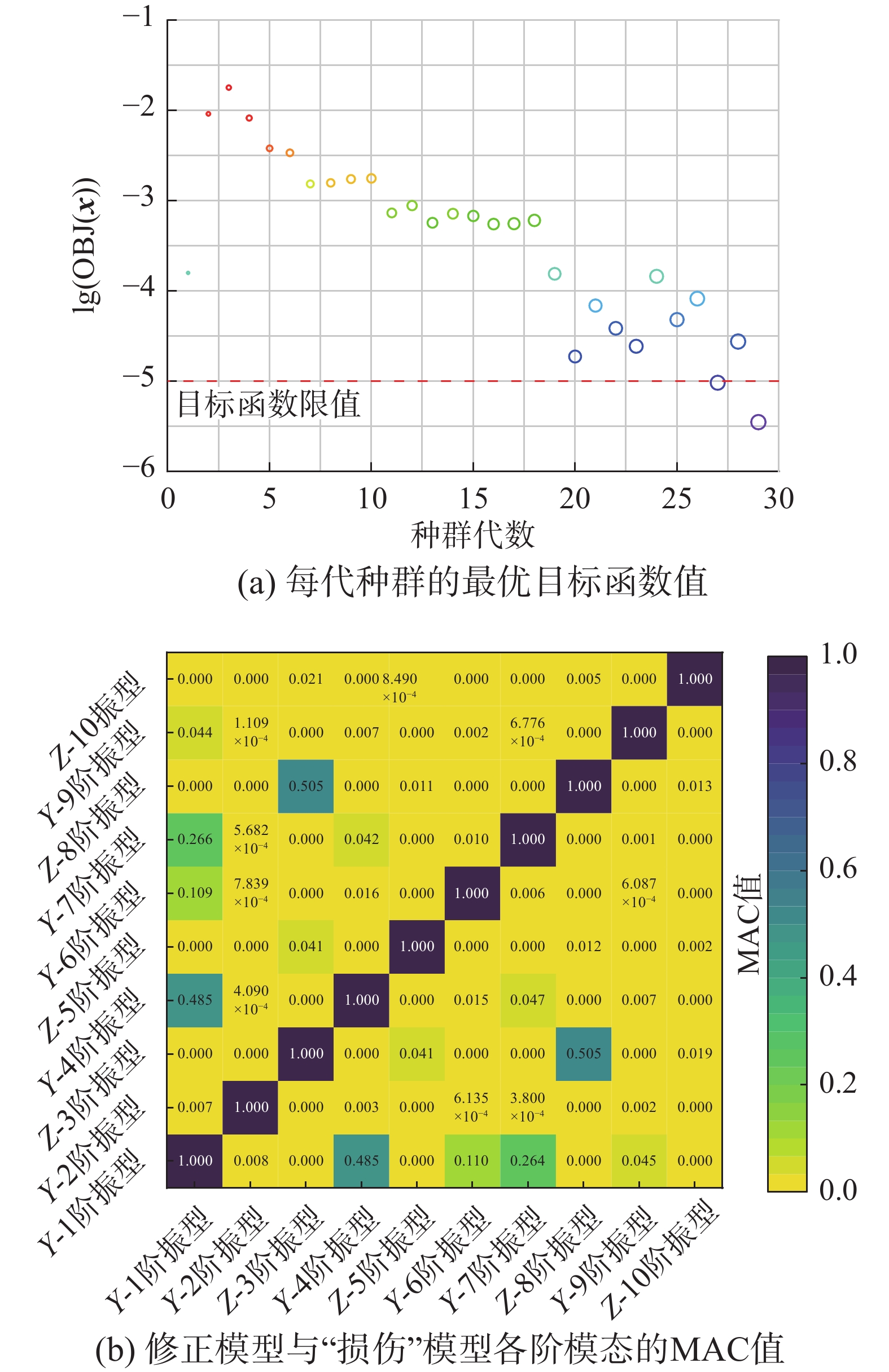
在本算例中，PSO算法中每一代的粒子规模取为72，由于该算例基于有限元模型生成结构损伤，精度较高，因此，优化时目标函数阈值设为1.0×10−5，模态识别的MAC阈值设为0.98。经过28次迭代后，目标函数达到1.0×10−5以下，每一次迭代中，目标函数的收敛过程如图4(a)所示，识别出的6个单元的惯性矩折减系数如表1所示，修正模型和“损伤”模型的前10阶振型的MAC矩阵如图4(b)。结果表明，本研究提出的程序框架可以准确识别简支梁中的损伤单元及对应损伤程度，计算误差在1%以下。
![]()
图 4 PSO迭代过程及损伤识别结果注：OBJ(x)参见式(1)Figure 4. The iterative process of the PSO algorithm and the damage identification results表 1 简支梁损伤识别结果Table 1. Damage identification results of the simply-supported beam单元编号 惯性矩折减系数 识别结果 误差/(%) 4 1.0 1.0000 0.00 5 0.3 0.2992 −0.27 9 1.0 1.0000 0.00 10 0.3 0.2984 −0.53 13 0.3 0.3029 0.97 14 1.0 1.0000 0.00 目标函数值：3.52×10−6 3.2 算例2-大跨度斜拉桥振动台试验
3.2.1 有限元模型介绍
本节以1∶35的苏通大桥振动台试验为研究对象，详细的试验模型设计见GUAN等[28]的研究，如图5(a)所示。首先，基于OpenSees建立试验桥梁的精细有限元模型，如图5(b)所示。其中，桥梁主塔和边墩采用RC空心截面，基于4节点分层壳单元ShellMITC4模拟；混凝土采用基于损伤力学和弥散裂缝模型二次开发的二维混凝土模型[16]；钢筋采用基于Steel02材料本构定义的PlateRebar材料；钢箱梁采用基于ShellMITC4的弹性壳单元模拟；斜拉索采用桁架单元；塔梁及塔墩之间的连接采用TwoNodeLink单元模拟。全桥模型包含9896个节点，15 473个单元。
3.2.2 更新参数
模型更新时，选择了包括混凝土弹性模量、塔梁/墩连接刚度、主梁厚度和材料弹性模量等11个更新参数。其中，更新主塔混凝土建模参数时，沿高度方向将其划分为三个区域，分别为塔顶混凝土、塔中混凝土和塔底混凝土，如图5(c)所示。同时，为体现南、北塔混凝土的材料性能差异，对两个桥塔的混凝土材料参数分别更新。上述更新参数及其对应的上、下限如表2所示，为了避免不同参数取值范围对模型更新结果的影响，优化时，各参数的变化范围统一映射至[90%, 110%]区间。
![]()
图 5 苏通大桥振动台试验及其有限元模型Figure 5. Shake table test of Sutong Bridge and the corresponding FE model3.2.3 模型更新结果
在本算例中，为了体现上述开源框架的可拓展性，分别对比了不同优化算法(GA和PSO)的计算精度与效率。优化时，每种算法的种群规模统一取为200，最大迭代次数为30，考虑试验测量误差等的影响，匹配实测振型与有限元模拟结果时，MAC阈值取为0.8，目标函数阈值取为1.0×10−4。
基于上述算法设置，采用12th Gen Intel® Core™ i9-12900K @ 3.19 GHz，64 G内存计算平台，调用平台中的20个线程，采用不同算法分别开展上述桥梁的模型更新，结果如表3所示。
表 2 模型更新参数上下限与更新结果Table 2. The updated results of the parameters序号 参数 参数上/下限 初始值 更新结果 1 南塔底部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 4.91×109 Pa 2 南塔中部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 3.23×109 Pa 3 南塔顶部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 2.88×109 Pa 4 北塔底部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 2.42×109 Pa 5 北塔中部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 8.18×109 Pa 6 北塔顶部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 3.17×109 Pa 7 钢箱梁弹性模量 [1.80×1011, 2.10×1011] 2.00×1011 Pa 1.96×1011 Pa 8 钢箱梁厚度 [8.00×10−3, 1.10×10−2] 1.00×10−2 m 8.00×10−3 m 9 塔-梁连接刚度 [1.00×105, 1.00×107] 1.00×106 N/m 4.71×106 N/m 10 1、4号墩-梁连接刚度 [1.00×105, 1.00×107] 1.00×106 N/m 5.71×105 N/m 11 2、3号墩-梁连接刚度 [1.00×105, 1.00×107] 1.00×106 N/m 3.66×105 N/m 表 3 不同算法的效率对比Table 3. Comparison of efficiency of different algorithms算法 PSO GA 目标函数值 5.36×10−5 5.86×10−4 种群迭代数量 24 30 计算时长 29 h10 min 38 h18 min 结果表明，对于上述苏通大桥振动台试验，PSO算法相比GA算法而言可以在更少的计算时间内获得更优的目标函数值，算法的效率和精度明显更优。在此基础上，统计PSO算法的更新过程如图6所示，最终参数更新结果如表2所示。图6中，每一个数据点代表一次图5(b)所示模型的模态分析，PSO算法经过24次迭代计算，一共生成5000(=(24+1)×200)个粒子，最优解的目标函数值达到5.36×10−5。基于PSO算法，本文所提出的计算框架更新过程共耗时约29 h10 min，相比单线程分析耗时(258 h18 min)加速约9倍，此外，当采用更多线程参与计算时，上述计算时间可以进一步缩短。
模型更新后，试验识别的桥梁模态频率和数值模拟结果的计算误差及MAC值如表4所示。结果表明，基于本文提出的开源程序框架，可以准确匹配实测获得的结构模态数据，实现复杂桥梁的模型更新，计算频率与试验模型的误差在1%以内。
表 4 更新结果对比Table 4. Comparison of the updating results振型 实测频率/Hz 更新频率/Hz 误差/(%) MAC值 主梁1阶对称横漂 0.5981 0.5988 0.12 0.9946 南塔的1阶横弯 2.2279 2.2350 0.32 0.8823 北塔的1阶横弯 2.4426 2.4405 −0.09 0.9428 主梁2阶对称横漂 2.6852 2.6723 −0.48 0.9457 主梁3阶对称横漂 3.6406 3.6251 −0.42 0.9813 3.2.4 更新模型验证
为了验证模型更新结果的准确性，本文进一步计算了模型更新前后，OpenSees模型在PGA=0.1 g的场地波输入下的地震响应。计算时，模型采用Rayleigh阻尼，阻尼比基于试验数据采用随机子空间方法识别并设置[11]。
模型更新前后，部分测点的计算响应与试验实测结果对比如图7所示。可以看出，特别是t=6.0 s之后，相比初始模型的较大偏差，更新模型计算结果与试验基本一致。为了量化模型更新前后的计算误差，采用计算数据和实测数据的相关性量化结构响应的预测精度，如式(3)所示：
{\rm{COR}}({{\boldsymbol{X}}},{{\boldsymbol{Y}}}) = \left| {\frac{{{\text{E}}\left[ {({{\boldsymbol{X}}} - {\mu_{X}})({{\boldsymbol{Y}}} - {\mu_{Y}})} \right]}}{{{{{{\sigma}} }_{X}}{{{{\sigma}} }_{Y}}}}} \right| (3) 式中：X为各个测点的实测时程响应；Y为各测点对应的计算时程响应；σX 和 σY表示 X 和Y的标准差；μX 和μY表示X和Y的均值；E[·]为数学期望算子。由式(3)可知，COR(X, Y)的结果区间为[0, 1]，且数值越大则计算响应与实测相关性越好，即计算精度越高。
基于式(3)计算出各测点在模型更新前后的计算结果精度如图7所示，结果表明：相比初始模型，更新模型模拟试验桥梁地震响应的计算精度大幅提升。因此，本文提出的开源程序框架适用于大跨复杂桥梁的精细有限元模型更新，可以大幅提升桥梁的数值模拟精度，为建立数据驱动的复杂桥梁高精度模型奠定基础。
![]()
图 7 有限元模型更新前后时程响应对比Figure 7. Comparison of time-history responses of the FE model before/after updating4 结论
大跨桥梁的运维、加固和优化都依赖高保真、精细化的数值模型，模型更新技术是复杂桥梁精细化和数据驱动建模的基础，既有研究多依赖商业软件平台，限制了相关研究的深入开展。本文基于开源有限元分析软件OpenSees和开源脚本编程语言Python，开发了适用于复杂工程结构模型更新的开源程序框架，在此基础上，以一个简支梁的损伤识别和苏通大桥振动台试验模型更新为例，验证了上述程序框架的计算效率和精度，主要结论如下：
(1)基于Python编写了Input.py、Parallel.py及Optimization.py三大程序功能模块，实现了上述程序框架中不同程序和功能模块的数据交互、程序调度及并行分析功能，继而通过选用合适的目标函数、更新参数和优化算法，完成了上述开源程序框架的开发。
(2)以一个损伤简支梁模型为例，开展了基于上述开源程序框架的结构损伤识别研究，结果表明，上述程序框架可以准确识别出简支梁中的损伤单元及对应损伤程度，计算误差在1%以下。
(3)基于12th Gen Intel® Core™ i9-12900K @ 3.20 GHz，64 G内存的计算平台，调用计算机中的20个线程实现了苏通大桥振动台试验模型的快速模型更新，更新后，各阶模态的计算误差在1%以内，相比单线程分析方案加速约9倍，验证了上述框架的计算效率。
(4)以苏通大桥的振动台试验为例，分别对比GA和PSO两种常用算法的更新效率，计算结果表明，本文所提出的程序框架接口灵活，便于拓展和二次开发。此外，相比而言，PSO算法有较高的计算精度和效率。
(5)采用更新前后的模型分别计算试验桥梁在PGA=0.1 g场地波下的地震响应，并与试验结果对比，进一步验证了上述程序框架的可靠性与计算精度。
-
![]()
图 2 程序框架的实现流程和部分关键代码
Figure 2. The flowchart and key code fragments of the program framework
![]()
图 4 PSO迭代过程及损伤识别结果
注：OBJ(x)参见式(1)
Figure 4. The iterative process of the PSO algorithm and the damage identification results
![]()
图 5 苏通大桥振动台试验及其有限元模型
Figure 5. Shake table test of Sutong Bridge and the corresponding FE model
![]()
图 7 有限元模型更新前后时程响应对比
Figure 7. Comparison of time-history responses of the FE model before/after updating
表 1 简支梁损伤识别结果
Table 1 Damage identification results of the simply-supported beam
单元编号 惯性矩折减系数 识别结果 误差/(%) 4 1.0 1.0000 0.00 5 0.3 0.2992 −0.27 9 1.0 1.0000 0.00 10 0.3 0.2984 −0.53 13 0.3 0.3029 0.97 14 1.0 1.0000 0.00 目标函数值：3.52×10−6 
下载: 导出CSV
表 2 模型更新参数上下限与更新结果
Table 2 The updated results of the parameters
序号 参数 参数上/下限 初始值 更新结果 1 南塔底部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 4.91×109 Pa 2 南塔中部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 3.23×109 Pa 3 南塔顶部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 2.88×109 Pa 4 北塔底部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 2.42×109 Pa 5 北塔中部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 8.18×109 Pa 6 北塔顶部混凝土弹性模量 [1.09×109, 1.09×1010] 1.09×1010 Pa 3.17×109 Pa 7 钢箱梁弹性模量 [1.80×1011, 2.10×1011] 2.00×1011 Pa 1.96×1011 Pa 8 钢箱梁厚度 [8.00×10−3, 1.10×10−2] 1.00×10−2 m 8.00×10−3 m 9 塔-梁连接刚度 [1.00×105, 1.00×107] 1.00×106 N/m 4.71×106 N/m 10 1、4号墩-梁连接刚度 [1.00×105, 1.00×107] 1.00×106 N/m 5.71×105 N/m 11 2、3号墩-梁连接刚度 [1.00×105, 1.00×107] 1.00×106 N/m 3.66×105 N/m
下载: 导出CSV
表 3 不同算法的效率对比
Table 3 Comparison of efficiency of different algorithms
算法 PSO GA 目标函数值 5.36×10−5 5.86×10−4 种群迭代数量 24 30 计算时长 29 h10 min 38 h18 min
下载: 导出CSV
表 4 更新结果对比
Table 4 Comparison of the updating results
振型 实测频率/Hz 更新频率/Hz 误差/(%) MAC值 主梁1阶对称横漂 0.5981 0.5988 0.12 0.9946 南塔的1阶横弯 2.2279 2.2350 0.32 0.8823 北塔的1阶横弯 2.4426 2.4405 −0.09 0.9428 主梁2阶对称横漂 2.6852 2.6723 −0.48 0.9457 主梁3阶对称横漂 3.6406 3.6251 −0.42 0.9813
下载: 导出CSV
-
[1] XU Y L, XIA Y. Structural health monitoring of long-span suspension bridges [M]. Abingdon: Spon Press, 2012: 39 − 74.
[2] EREIZ S, DUVNJAK I, JIMENÉZ-ALONSO J F. Review of finite element model updating methods for structural applications [J]. Structures, 2022, 41: 684 − 723. doi: 10.1016/j.istruc.2022.05.041
[3] MARWALA T. Finite element model updating using computational intelligence techniques: Applications to structural dynamics [M]. London: Springer, 2010: 49 − 102.
[4] MARWALA T, BOULKAIBET I, ADHIKARI S. Probabilistic finite element model updating using Bayesian statistics: Applications to aeronautical and mechanical engineering [M]. Hoboken: John Wiley & Sons, 2016: 42 − 61.
[5] ZHU Q, XU Y L, XIAO X. Multiscale modeling and model updating of a cable-stayed bridge. I: Modeling and influence line analysis [J]. Journal of Bridge Engineering, 2015, 20(10): 04014112. doi: 10.1061/(ASCE)BE.1943-5592.0000722
[6] TRAN-NGOC H, KHATIR S, DE ROECK G, et al. Model updating for Nam O bridge using particle swarm optimization algorithm and genetic algorithm [J]. Sensors, 2018, 18(12): 4131. doi: 10.3390/s18124131
[7] 许世展, 李杨, 冯冠杰, 等. 基于响应面法的桥梁节段参数模型修正[J]. 铁道科学与工程学报, 2022, 19(6): 1658 − 1665. doi: 10.19713/j.cnki.43-1423/u.t20210725 XU Shizhan, LI Yang, FENG Guanjie, et al. Model updating of bridge segment parameter based on response surface method [J]. Journal of Railway Science and Engineering, 2022, 19(6): 1658 − 1665. (in Chinese) doi: 10.19713/j.cnki.43-1423/u.t20210725
[8] 胡俊亮, 颜全胜, 郑恒斌, 等. 基于Kriging模型的钢管混凝土连续梁拱桥有限元模型修正[J]. 振动与冲击, 2014, 33(14): 33 − 39. doi: 10.13465/j.cnki.jvs.2014.14.007 HU Junliang, YAN Quansheng, ZHENG Hengbin, et al. CFST arch/continuous beam bridge FEM model updating based on Kriging model [J]. Journal of Vibration and Shock, 2014, 33(14): 33 − 39. (in Chinese) doi: 10.13465/j.cnki.jvs.2014.14.007
[9] JONES D R. A taxonomy of global optimization methods based on response surfaces [J]. Journal of Global Optimization, 2001, 21(4): 345 − 383. doi: 10.1023/A:1012771025575
[10] 蒋伟, 刘纲. 基于多链差分进化的贝叶斯有限元模型修正方法[J]. 工程力学, 2019, 36(6): 101 − 108. doi: 10.6052/j.issn.1000‐4750.2018.04.0229 JIANG Wei, LIU Gang. Bayesian finite element model updating method based on multi-chain differential evolution [J]. Engineering Mechanics, 2019, 36(6): 101 − 108. (in Chinese) doi: 10.6052/j.issn.1000‐4750.2018.04.0229
[11] LIN K Q, XU Y L, LU X Z, et al. Cluster computing-aided model updating for a high-fidelity finite element model of a long-span cable-stayed bridge [J]. Earthquake Engineering & Structural Dynamics, 2020, 49(9): 904 − 923.
[12] XIAO X, XU Y L, ZHU Q. Multiscale modeling and model updating of a cable-stayed bridge. II: Model updating using modal frequencies and influence lines [J]. Journal of Bridge Engineering, 2015, 20(10): 04014113. doi: 10.1061/(ASCE)BE.1943-5592.0000723
[13] 夏志远, 李爱群, 李建慧, 等. 基于GMPSO的有限元模型修正方法验证[J]. 工程力学, 2019, 36(10): 66 − 74. doi: 10.6052/j.issn.1000-4750.2018.09.0506 XIA Zhiyuan, LI Aiqun, LI Jianhui, et al. Validation of finite element model updating methodology based on GMPSO [J]. Engineering Mechanics, 2019, 36(10): 66 − 74. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.09.0506
[14] XIA Z Y, LI A Q, LI J H, et al. Model updating of an existing bridge with high-dimensional variables using modified particle swarm optimization and ambient excitation data [J]. Measurement, 2020, 159: 107754. doi: 10.1016/j.measurement.2020.107754
[15] 解琳琳, 黄羽立, 陆新征, 等. 基于OpenSees的RC框架-核心筒超高层建筑抗震弹塑性分析[J]. 工程力学, 2014, 31(1): 64 − 71. doi: 10.6052/j.issn.1000-4750.2013.07.0591 XIE Linlin, HUANG Yuli, LU Xinzheng, et al. Elasto-plastic analysis for super tall RC frame-core tube structures based on OpenSees [J]. Engineering Mechanics, 2014, 31(1): 64 − 71. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.07.0591
[16] LU X Z, XIE L L, GUAN H, et al. A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees [J]. Finite Elements in Analysis and Design, 2015, 98: 14 − 25. doi: 10.1016/j.finel.2015.01.006
[17] 林楷奇, 解琳琳, 陆新征, 等. 基于开源计算程序的特大跨斜拉桥地震灾变及倒塌分析[J]. 工程力学, 2016, 33(1): 72 − 80. doi: 10.6052/j.issn.1000-4750.2014.06.0541 LIN Kaiqi, XIE Linlin, LU Xinzheng, et al. Earthquake-induced collapse simulation of a super long span cable-stayed bridge based on an open source FE program [J]. Engineering Mechanics, 2016, 33(1): 72 − 80. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.06.0541
[18] Python. Concurrent execution [CP/OL]. https://docs.python.org/3/library/concurrency.html, 2023-8-24.
[19] Guofei9987. scikit-opt [CP/OL]. https://gitee.com/guofei9987/scikit-opt, 2021-06-28.
[20] ALKAYEM N F, CAO M S, ZHANG Y F, et al. Structural damage detection using finite element model updating with evolutionary algorithms: A survey [J]. Neural Computing and Applications, 2018, 30(2): 389 − 411. doi: 10.1007/s00521-017-3284-1
[21] 伊廷华, 王传伟, 李宏男. 利用分布式狼群算法进行三维传感器优化布置的方法研究[J]. 振动工程学报, 2014, 27(5): 668 − 675. doi: 10.3969/j.issn.1004-4523.2014.05.004 YI Tinghua, WANG Chuanwei, LI Hongnan. Optimal triaxial sensor placement using distributed wolf algorithm [J]. Journal of Vibration Engineering, 2014, 27(5): 668 − 675. (in Chinese) doi: 10.3969/j.issn.1004-4523.2014.05.004
[22] LIN K Q, XU Y L, LU X Z, et al. Time history analysis-based nonlinear finite element model updating for a long-span cable-stayed bridge [J]. Structural Health Monitoring, 2021, 20(5): 2566 − 2584. doi: 10.1177/1475921720963868
[23] KENNEDY J, EBERHART R. Particle swarm optimization [C]// IEEE International Conference On Neural Networks. Perth: IEEE, 1995: 1942 − 1948.
[24] Zhengjunhao11. Model-updating-framework [CP/OL]. https://github.com/zhengjunhao11/model-updating-framework, 2023-01-20.
[25] 万华平, 任伟新, 魏锦辉. 基于高斯过程响应面的结构有限元模型修正方法[J]. 振动与冲击, 2012, 31(24): 82 − 87. doi: 10.3969/j.issn.1000-3835.2012.24.017 WANG Huaping, REN Weixin, WEI Jinhui. Structural finite element model updating based on Gaussian process response surface methodology [J]. Journal of Vibration and Shock, 2012, 31(24): 82 − 87. (in Chinese) doi: 10.3969/j.issn.1000-3835.2012.24.017
[26] 安平和, 邬晓光. 基于支持向量机的梁桥多位置损伤识别研究[J]. 铁道科学与工程学报, 2019, 16(5): 1231 − 1236. doi: 10.19713/j.cnki.43-1423/u.2019.05.016 AN Pinghe, WU Xiaoguang. Multi position damage identification of beam-bridges based on support vector machine [J]. Journal of Railway Science and Engineering, 2019, 16(5): 1231 − 1236. (in Chinese) doi: 10.19713/j.cnki.43-1423/u.2019.05.016
[27] 李洪泉, 董亮, 吕西林. 基于小波变换的结构损伤识别与试验分析[J]. 土木工程学报, 2003, 36(5): 52 − 57, 75. doi: 10.3321/j.issn:1000-131X.2003.05.009 LI Hongquan, DONG Liang, LYU Xilin. Identification of structural damage and test study based on wavelet transform [J]. China Civil Engineering Journal, 2003, 36(5): 52 − 57, 75. (in Chinese) doi: 10.3321/j.issn:1000-131X.2003.05.009
[28] GUAN Z G, LI J Z, GUO W, et al. Design and validation of a shaking-table test model on a long-span cable-stayed bridge with inverted-Y-shaped towers [J]. Engineering Structures, 2019, 201: 109823. doi: 10.1016/j.engstruct.2019.109823
计量
- 文章访问数: 390
- HTML全文浏览量: 81
- PDF下载量: 127
