中低雷诺数下拦污栅结构动态绕流数值模拟

杨家富; 骆佳玲; 王文全

doi:10.6052/j.issn.1000-4750.2022.12.1071

中低雷诺数下拦污栅结构动态绕流数值模拟

四川大学水力学与山区河流开发保护国家重点实验室，四川，成都 610065

基金项目: 国家自然科学基金项目(52179087)

详细信息

作者简介:
杨家富(2000−)，男，四川叙州人，硕士生，主要从事流体力学方面的研究(E-mail: 254207814@qq.com)

骆佳玲(1997−)，女，湖南岳阳人，博士生，主要从事流体力学方面的研究(E-mail: 244210807@qq.com)

通讯作者:
王文全(1977−)，男，四川南充人，教授，博士，博导，主要从事多场耦合力学方面的研究(E-mail: wwqquan@126.com)

中图分类号: TV732.2
计量
- 文章访问数: 166
- HTML全文浏览量: 58
- PDF下载量: 27
出版历程
- 收稿日期: 2022-12-13
- 修回日期: 2023-04-11
- 网络出版日期: 2023-05-05
- 刊出日期: 2025-04-24

NUMERICAL SIMULATION OF THE FLOW CHARACTERISTICS AROUND A TRASH RACK AT LOW AND MEDIUM REYNOLDS NUMBER

State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu , Sichuan 610065, China

摘要

摘要:
拦污栅下游闸门在动态启闭过程中，拦污栅将在不同流动雷诺数下工作，其水动力动态特性备受关注。为此，基于高时空分辨率的Incompact3d开源软件构架，采用浸入边界法处理复杂流固边界，研究了拦污栅在中低流动雷诺数下(Re≤3900)的水动力特性。结果表明：在中低流动雷诺数下，拦污栅的水动力特性与前缘涡脱落和尾迹涡的生成紧密相关，升、阻力系数都呈现周期性变化趋势。随着雷诺数增大，拦污栅时间平均阻力系数呈现逐渐降低的趋势，但升、阻力系数的频率逐渐增加。同时发现在Re≤3900时，随着栅条间距的减小，拦污栅时间平均阻力系数呈现逐渐升高的趋势，但升、阻力系数的频率逐渐降低。
- 拦污栅 /
- 水动力特性 /
- 涡量分布 /
- 数值模拟 /
- 高保真
Abstract:
During the opening or closing of the downstream gate of trash rack, the trash rack will work at different flow Reynolds numbers, and its hydrodynamic characteristics are of great interest to researchers. To this end, the hydrodynamic characteristics of the trash rack at low and medium flow Reynolds numbers (Re≤3900) are investigated in detail. The Incompact3d open-source software framework with a high spatial and temporal resolution is used to solve the flow, and the fluid-solid boundary is dealt with using the immersed boundary method. The results show that the hydrodynamic characteristics of the trash rack at low and medium flow Reynolds numbers are closely related to the shedding of the leading-edge vortex and the generation of the trailing vortex, and the lift and drag coefficients show a periodic trend. As the Reynolds number increases, the time-averaged drag coefficient shows a trend of gradually decreasing, but the frequency of the drag and lift coefficient gradually increases. It is also found that the time-averaged drag coefficient shows a trend of gradually increase with the decrease of the fence spacing at Re≤3900, although the frequency of the drag and lift coefficient decreases gradually.
- trash rack /
- hydrodynamic characteristics /
- vorticity /
- numerical simulation /
- high fidelity

HTML全文

拦污栅是电站、泵站等水工建筑物中一个不可或缺的重要设施，一般布置在进水口处，防止漂浮物进入水力机械内部流道，在保障水力发电机组和泵站的安全性方面发挥着重要的作用^[1-5]。水流通过拦污栅受到影响，属于典型的格栅紊流。例如，李春光^[6]发现主动格栅紊流对钝体型断面颤振导数的影响随着流速上升而增大。黄睿等^[7]发现双层横向振荡格栅中心区域平均流速近似为零。肖金龙^[8]研究了泥沙颗粒沉降过程中对振荡格栅紊流影响，发现泥沙颗粒粒径对紊动动能的影响不明显。同时，现阶段对于拦污栅的研究，大多数学者从减小水力损失以及形状优化的角度出发。例如， MILTENOVIC等^[9]提出了一种新的电力驱动的精细水平拦污栅，以实现更好的清洁和拦污功能。LATIF^[10]针对拦污栅水头损失大、堵塞率偏高的问题进行了形体优化，得到水力损失最小的栅条间距。LUČIN等^[11]研究了拦污栅水力损失的来源，提出了系统的拦污栅几何优化方案。高学平等^[12]研究了有无栅条对水力损失和流速分布的影响，发现有栅结构使得流速分布更均匀，且水力损失仅增加7.2%。但上述研究主要集中在闸门全开的正常运行工况，而闸门动态启闭过程中，由于流动雷诺数的大幅变化，拦污栅结构的动态绕流特性将发生显著的变化，从而引起结构受力的变化，即栅条上漩涡脱落产生的侧向推力和顺向曳引力^[13]，可能会导致其振动甚至共振而受损破坏。尤其是中低雷诺数流动阶段(如对于栅条厚度0.02 m，流速小于0.2 m/s阶段，也即雷诺数≤3900)，其水动力学特性很少被研究。同时，上述研究都是基于低阶格式的数值方法和雷诺时均的湍流模型，计算准确性有待提高。为此，本文基于Incompact3d高保真数值构架，采用六阶紧致差分格式的直接数值模拟来求解控制方程，通过浸入边界法处理流固界面信息交换^[14-17]，可以更加准确地预测中低雷诺数下复杂拦污栅结构的水动力特性，为拦污栅结构的优化设计提供参考。

1 控制方程与数值方法

1.1 控制方程

不可压缩流体的质量和动量平衡的无量纲偏微分方程可以表示为：

$\nabla \cdot {\boldsymbol{u}} = 0$

(1)

$\frac{{\partial {\boldsymbol{u}}}}{{\partial t}} = - {\boldsymbol{u}} \cdot \nabla {\boldsymbol{u}} - \nabla p + \upsilon {\nabla ^2}{\boldsymbol{u}} + {\boldsymbol{f}}$

(2)

式中： ${\boldsymbol{u}}$ 为速度矢量；t为时间；p为压力； $\upsilon$ 为运动粘度； ${\boldsymbol{f}}$ 为通过浸入边界法处理边界时产生的施加在固体上的力，以确保流体-固体界面上的无滑移条件^[18]。

为了减少对流项离散格式引起的数值误差，非线性对流项通常采用斜对称形式，即：

$\frac{{\partial {\boldsymbol{u}}}}{{\partial t}} = - \frac{1}{2}\left[ {\nabla \left( {{\boldsymbol{u}} \cdot {\boldsymbol{u}}} \right) + \left( {{\boldsymbol{u}} \cdot \nabla } \right){\boldsymbol{u}}} \right] - \nabla p + \upsilon {\nabla ^2}{\boldsymbol{u}} + {\boldsymbol{f}}$

(3)

1.2 数值方法

为了数值求解控制方程式(1)和式(3)，本文采用紧致的六阶有限差分格式进行空间离散，基于二阶Adams-Bashforth格式进行时间推进。为了处理不可压缩条件，采用分步投影方法求解压力泊松方程，并通过快速傅立叶变换在谱空间中求解。

1.2.1 时间推进

采用二阶Adams-Bashfort方法离散时间项，和定义为中间速度。这些中间速度通过分步投影法计算，则式(3)的时间推进可以表示为：

$\frac{{{{\boldsymbol{u}}^*} - {{\boldsymbol{u}}^k}}}{{\Delta t}} = \frac{3}{2}{{\boldsymbol{F}}^k} - \frac{1}{2}{{\boldsymbol{F}}^{k - 1}} - \nabla {\tilde p^k} + {{\boldsymbol{\tilde f}}^{k + 1}}$

(4)

$\frac{{{{\boldsymbol{u}}^{**}} - {{\boldsymbol{u}}^*}}}{{\Delta t}} = \nabla {\tilde p^k}$

(5)

$\frac{{{{\boldsymbol{u}}^{k + 1}} - {{\boldsymbol{u}}^{**}}}}{{\Delta t}} = - \nabla {\tilde p^{k + 1}}$

(6)

${{\boldsymbol{F}}^k} = - \frac{1}{2}[ {\nabla ( {{{\boldsymbol{u}}^k} \otimes {{\boldsymbol{u}}^k}} ) + ( {{{\boldsymbol{u}}^k}.\nabla } ){{\boldsymbol{u}}^k}} ] + \upsilon {\nabla ^2}{{\boldsymbol{u}}^k}$

(7)

${\tilde p^{k + 1}} = \frac{1}{{\Delta t}}\int_{{t_k}}^{{t_{k + 1}}} {p\;{\rm{d}}t,\;\;{{{\boldsymbol{\tilde f}}}^{k + 1}}} = \frac{1}{{\Delta t}}\int_{{t_k}}^{{t_{k + 1}}} {{\boldsymbol{f}}\;{\rm{d}}t}$

(8)

压力项和力源项由给定时间步长上的时间平均值 $\Delta t$ ( $\Delta t{\text{ = }}{t_{n + 1}} - {t_n}$ )表示，用 ${\tilde p^{k + 1}}$ 和 ${{\boldsymbol{\tilde f}}^{k + 1}}$ 表示。

1.2.2 对流项和粘性项处理

采用高阶紧致差分格式离散空间中的对流项和粘性项。一阶导数的展开式为：

$\alpha f_{i - 1}'+ f_i'+ \alpha f_{i + 1}' = a\frac{{{f_{i + 1}} - {f_{i - 1}}}}{{2\Delta x}} + b\frac{{{f_{i + 2}} - {f_{i - 2}}}}{{4\Delta x}}$

(9)

式中， $\alpha = 1/3、\;a = 14/9、\;b = 1/9$ ^[19]，这种近似具有六阶精度。

二阶导数的展开式为：

$\alpha f_{i - 1}^{''} + f_i^{''} + \alpha f_{i + 1}^{''} = a\frac{{{f_{i + 1}} - 2{f_i} + {f_{i - 1}}}}{{\Delta {x^2}}} +$

$\qquad b\frac{{{f_{i + 2}} - 2{f_i} + {f_{i - 2}}}}{{4\Delta {x^2}}} + c\frac{{{f_{i + 3}} - 2{f_i} + {f_{i - 3}}}}{{9\Delta {x^2}}}$

(10)

式中， $\alpha = 2/11、\;a = 12/11、\;b = 3/11、\;c = 0$ ^[19]。

式(7)中由 ${{\boldsymbol{F}}^k}$ 表示的对流项和粘性项的偏微分采用等式(9)和式(10)的高阶紧致格式进行计算。

1.2.3 压力项处理

泊松方程基于高阶有限差分格式^[20-21]在物理空间中表示时，其计算成本会很高。相反，如果在傅里叶空间中执行等效的运算，在快速傅里叶变换的帮助下，成本更低且易于实现。

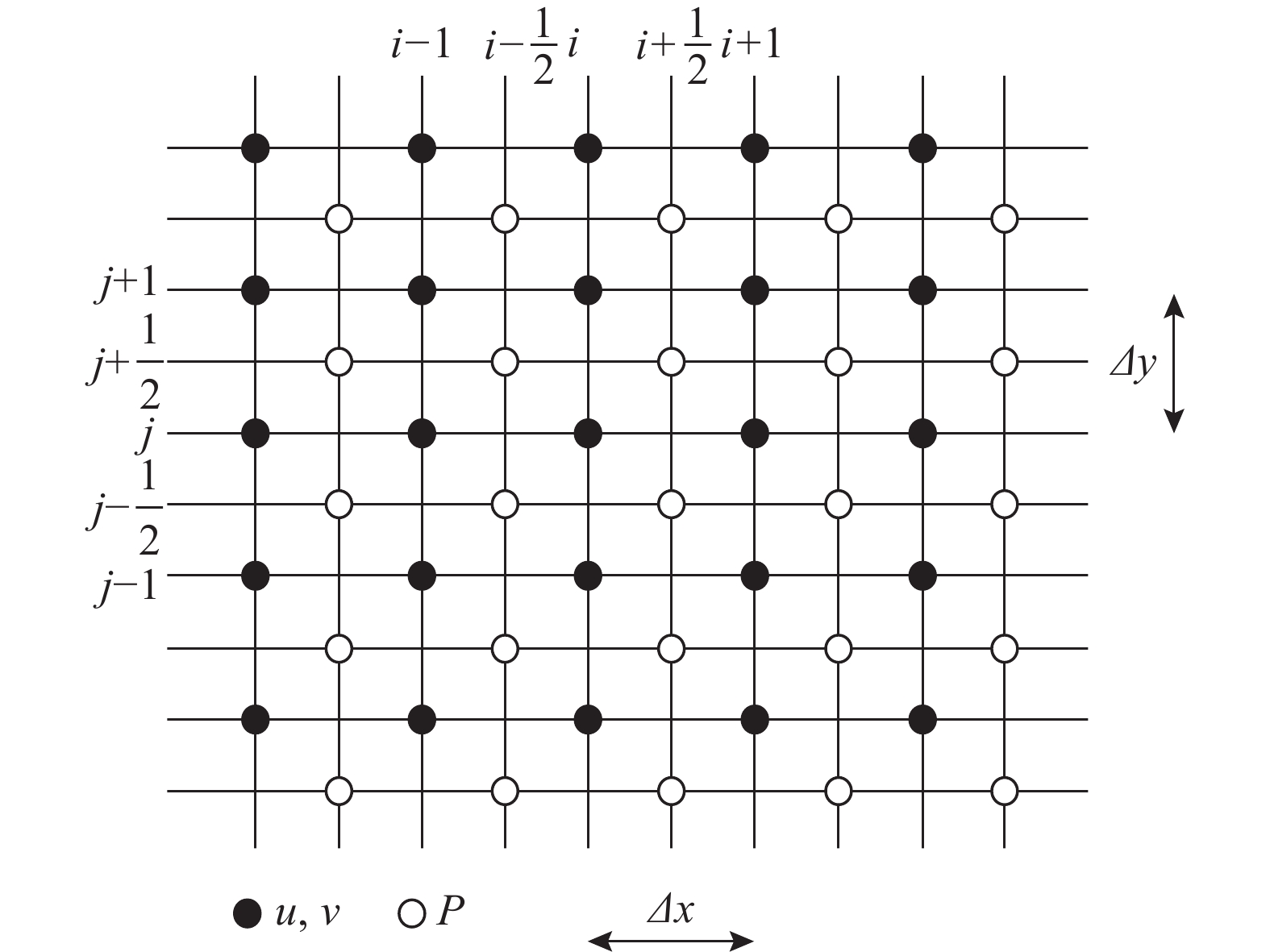
采用交错网格存储压力与速度变量(交错网格，见)，为了通过半网格 $\Delta x/2$ 计算交错节点处一阶导数 ${f'_{i + 1/2}}$ 的值，六阶有限差分格式可以表示为：

图 1 交错网格的二维变量排列

Figure 1. Two-dimensional variable arrangement of staggered (right) lattices

下载: 全尺寸图片幻灯片

$\frac{9}{{62}}{f'_{i - 1/2}} + {f'_{i + 1/2}} + \frac{9}{{62}}{f'_{i + 3/2}} = \frac{{63}}{{62}}\frac{{{f_{i + 1}} - {f_i}}}{{\Delta x}} + \frac{{17}}{{62}}\frac{{{f_{i + 2}} - {f_{i - 1}}}}{{3\Delta x}}$

(11)

${f_{i + 1/2}}$ 的具有六阶精度的近似值可以表示为：

$\frac{3}{{10}}{f'_{i - 1/2}} + {f'_{i + 1/2}} + \frac{3}{{10}}{f'_{i + 3/2}} = \frac{3}{4}\frac{{{f_{i + 1}} + {f_i}}}{2} + \frac{1}{{20}}\frac{{{f_{i + 2}} + {f_{i - 1}}}}{2}$

(12)

对于周期性或自由滑移边界条件下的压力项的处理，快速傅里叶方法的求解过程如下：

假设f是在定义区间 $\left[ {0\;,\;{L_x}} \right]$ 上的周期函数，即：

$f(x + {L_x}) = f(x)$

(13)

当 $- {n_x}/2 \leqslant l \leqslant {n_x}/2 - 1$ 时，离散傅里叶变换可定义为：

${\hat f_l} = \frac{1}{{{n_x}}}\sum\limits_{i = 2}^{{n_x}} {{f_i}\;{{\rm{e}}^{ - \sqrt {{{ - }}1} \cdot 2\pi l{x_i}/{L_x}}}}$

(14)

其逆表达式为：

${f_i} = \sum\limits_{l = - {n_x}/2}^{{n_x}/2 - 1} {{{\hat f}_l}\;{{\rm{e}}^{ - \sqrt {{{ - }}1} \cdot 2\pi l{x_i}/{L_x}}}}$

(15)

对于交错网格，只需要基于中心点进行等效移位变换 $i \to i + 1/2$ ，进行预处理和后处理后可以使用传统的快速傅里叶变换进行计算。

假设f在x=0和x=L_x对称，即：

$f(x) = f({{ - }}x)$

(16)

$f(x + {L_x}) = f({L_x}{{ - }}x)$

(17)

则当 $0 \leqslant l \leqslant {n_x} - 1$ 时，离散余弦傅里叶变换可以定义为：

${\hat f_l} = \frac{2}{{{n_x}{{ - }}1}}\left[ {\frac{1}{2}{f_1} + f'} \right]$

(18)

$f' = \sum\limits_{i = 2}^{{n_x} - 1} {{f_i}\;\cos (2\pi l{x_i}/{L_x})} + \frac{1}{2}{\left( { - 1} \right)^l}{f_{{n_x}}}$

(19)

其逆表达式为：

${f_i} = \frac{{{{\hat f}_0}}}{2} + \sum\limits_{l = 1}^{{n_x} - 2} {{{\hat f}_l}\cos (2\pi l{x_i}/{L_x}) + \frac{1}{2}{{\left( { - 1} \right)}^{i + 1}}{{\hat f}_{{n_x} - 1}}}$

(20)

等效的移位变换与前面的表达式略有不同。当 $0 \leqslant l \leqslant {n_x} - 2$ 时，离散余弦傅里叶变换可定义为：

${\hat f_l} = \frac{2}{{{n_x}{{ - }}1}}\sum\limits_{i = 1}^{{n_x} - 1} {{f_{i{\text{ + }}1/2}}\;\cos (2\pi l{x_{i{\text{ + }}1/2}}/{L_x})}$

(21)

${f_{i{\text{ + }}1/2}} = \frac{{{{\hat f}_0}}}{2} + \sum\limits_{l = 1}^{{n_x} - 2} {{{\hat f}_l}\cos (2\pi l{x_{i{\text{ + }}1/2}}/{L_x})}$

(22)

在分步法中，可以通过求解泊松方程在每个子时间步结束时验证等式(1)。

$\nabla \cdot {{\boldsymbol{u}}^{k + 1}} = 0$

(23)

$\nabla \cdot \nabla {\widetilde p^{k + 1}} = \frac{{\nabla .{{\boldsymbol{u}}^{**}}}}{{\Delta t}}$

(24)

进一步将高阶紧致有限差分格式与浸入边界法相结合，以解决复杂几何结构流体流动问题的模拟。采用直接力源法，式(4)中的力源项可以表示为：

${{\boldsymbol{\tilde f}}^{k + 1}} = - \frac{3}{2}{{\boldsymbol{F}}^k} + \frac{1}{2}{{\boldsymbol{F}}^{k - 1}} + \nabla {\tilde p^k} + \frac{{{{\boldsymbol{u}}^*} - {{\boldsymbol{u}}^k}}}{{\Delta t}}$

(25)

1.2.4 力的计算

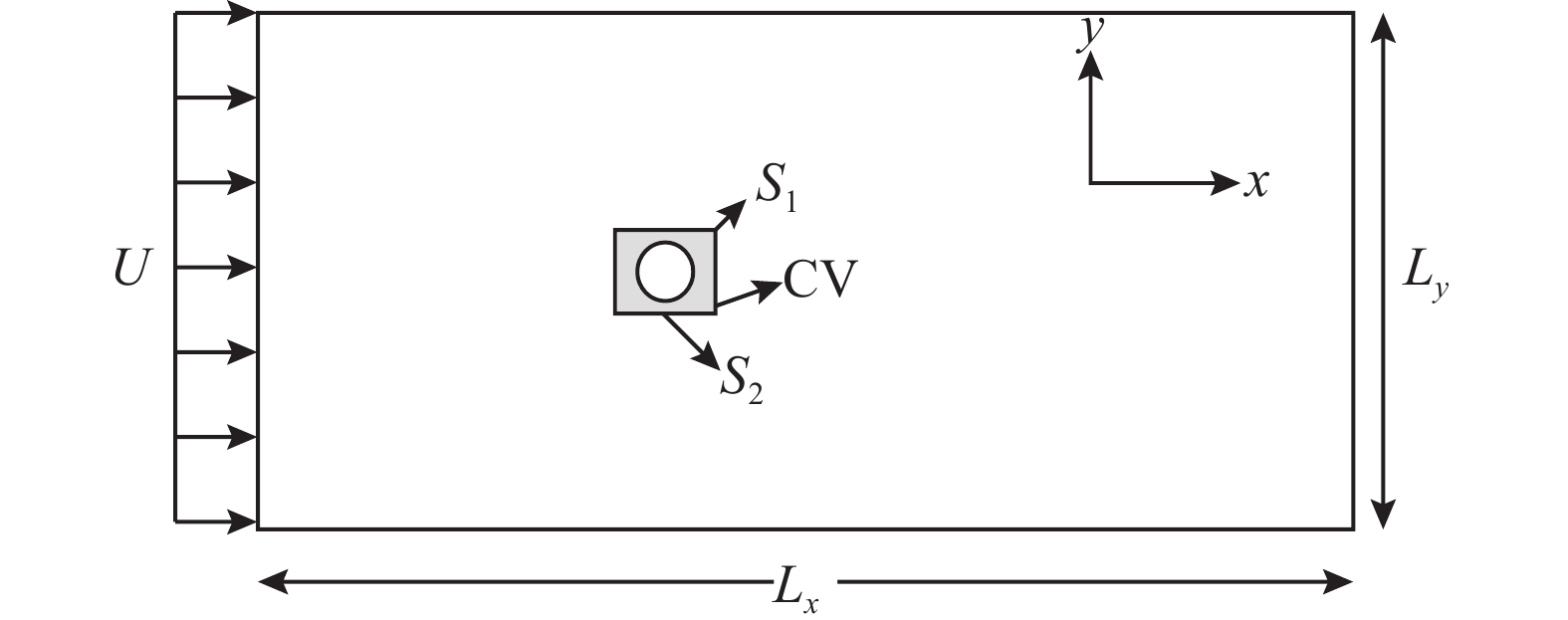
作用在固体上的力是通过在固体周围定义的矩形控制体积中应用积分动量方程来计算的，见图2。图中阴影部分CV控制体内的动量变化率应该等于作用在控制体上的外力和，其无量纲形式的积分动量方程表示为：

$\sum {{\boldsymbol{F}}_{{\text{ext}}}}{\text{ = }}{{\boldsymbol{F}}_{\boldsymbol{1}}}{\text{ + }}{{\boldsymbol{F}}_{\boldsymbol{2}}}{\text{ = }}\frac{\partial }{{\partial t}}\int_{{\text{CV}}} {{\boldsymbol{u}}{\text{d}}V + } \int_{{{{S}}_{\text{1}}} \cup {{{S}}_{\text{2}}}} {{\boldsymbol{u}}({\boldsymbol{u}} \cdot {\boldsymbol{n}}){\text{d}}A}$

(26)

式中： ${{\boldsymbol{F}}_1}$ 和 ${{\boldsymbol{F}}_{\boldsymbol{2}}}$ 分别为流体对控制面S₁和控制面S₂的作用力； ${\boldsymbol{n}}$ 为垂直于控制面的单位矢量。事实上，控制面S₁也是固体边界面，通过其表面的动量通量为零，因此只需求出 ${{\boldsymbol{F}}_{\boldsymbol{2}}}$ ，由式(26)就可求出 ${{\boldsymbol{F}}_1}$ ，正好 ${{\boldsymbol{F}}_1}$ 就是需要求的流体作用在固体边界上的力。

图 2 力计算的控制体积示意图

Figure 2. Schematic diagram of the control volume for force calculation

下载: 全尺寸图片幻灯片

根据表面S₂上压力和粘性应力的积分， ${{\boldsymbol{F}}_{{2}}}$ 计算如下：

${{\boldsymbol{F}}_{{2}}}{\text{ = }}\int_{{{{S}}_{\text{2}}}} {\left[ { - p{\boldsymbol{I}} + \frac{1}{{{Re} }}( {\nabla {\boldsymbol{u}} + {{( {\nabla {\boldsymbol{u}}} )}^T}} )} \right]{\boldsymbol{n}}{\text{d}}S}$

(27)

结合式(26)和式(27)， ${{\boldsymbol{F}}_1}$ 可由下式进行估算：

$\begin{split} {{\boldsymbol{F}}_1}{\text{ = }}&\frac{\partial }{{\partial t}}\int_{{\text{CV}}} {{\boldsymbol{u}}{\text{d}}V + } \int_{{{{S}}_{\text{2}}}} {{\boldsymbol{u}}({\boldsymbol{u}} \cdot {\boldsymbol{n}}){\text{d}}A} -\\& \int_{{{{S}}_{\text{2}}}} {\left[ { - p{\boldsymbol{I}} + \frac{1}{{{Re} }}( {\nabla {\boldsymbol{u}} + {{( {\nabla {\boldsymbol{u}}} )}^T}} )} \right]{\boldsymbol{n}}{\text{d}}S} \end{split}$

(28)

式中：I为单位矩阵。可以使用 ${{\boldsymbol{F}}_1}$ 的笛卡尔分量计算阻力系数 $C_{\text{D}}$ 和升力系数 $C_{\text{L}}$ ：

$C_{\text{D}} = - {{\boldsymbol{F}}_1} \cdot {n_x}$

(29)

$C_{\text{L}} = - {{\boldsymbol{F}}_1} \cdot {n_y}$

(30)

式中： ${n_x}$ 和 ${n_y}$ 为力的单位向量。对于非定常流动，斯特劳哈数St定义为漩涡从柱体上脱落的无量纲频率：

${St} = \frac{{fD}}{U}$

(31)

式中： $f$ 为漩涡脱落频率； $D$ 为特征长度；U为进口速度。

2 验证算例

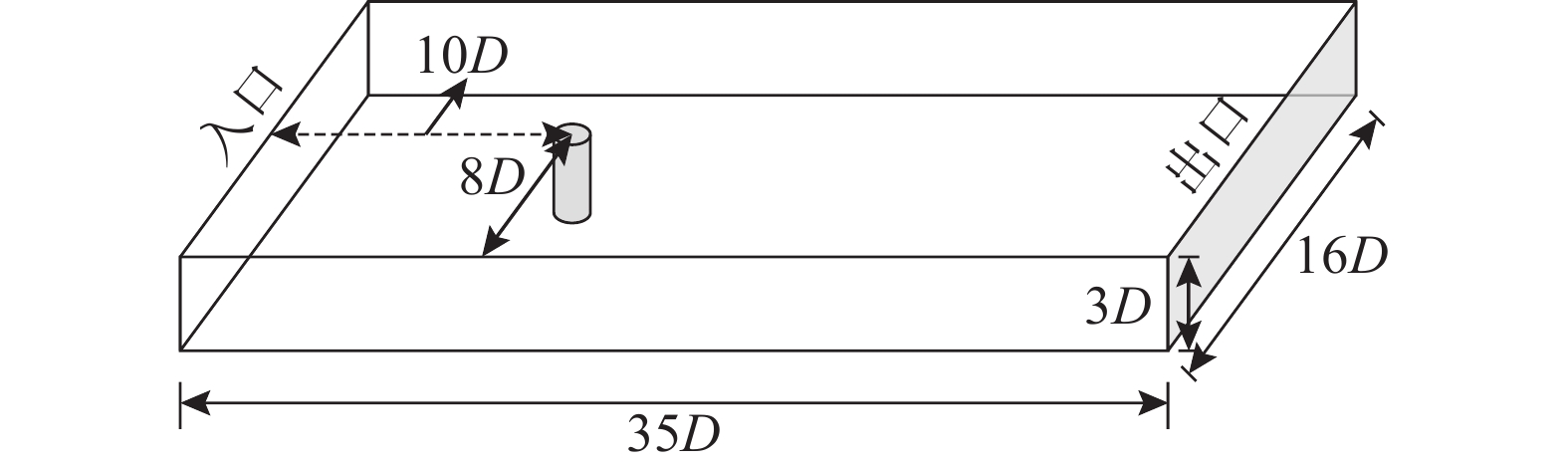
如图3所示，计算域为一矩形区域，计算域的大小为L_x×L_y×L_z= 35D×16D×3D，圆柱中心的坐标为(8D, 10D, 1.5D)。网格大小划分为 ${n_x} \times {n_y} \times {n_{\textit z}} = 361 \times 217 \times 64$ 。其中计算时间步长 $\Delta t =$ $0.001$ 。入口设置为均匀来流，出口设置为零压力梯度边界。计算域上下和前后面均设置为周期性边界条件，圆柱表面为固壁无滑移边界条件。流动雷诺数 ${{Re = }}\dfrac{{U{{D}}}}{\nu } = 3900$ 。其中： $\nu$ 为流体的流体运动粘度； $U$ 为入口速度；D为特征长度，取为圆柱直径。

图 3 计算域的示意图

Figure 3. Schematic diagram of the calculation domain

下载: 全尺寸图片幻灯片

表1列出了不同研究之间的数值结果对比。虽然不同的计算方法之间存在微小的差异，本文的计算结果与这些文献的数值模拟结果总体上比较接近，证实本文的计算结果是可靠的。同时，在计算时间上，本文比较了采用Fluent软件中RANS模型进行比较。表2列出了圆柱绕流分别采用DNS和RANS计算结果的比较(计算机都采用RTX2080Ti+AMD Epyc 7702 64核进行并行计算)。由表2可见，由于本文在求解压力泊松方程时采用快速傅里叶变换方法求解，大大提高了计算效率，并且使用高保真的直接数值模拟方法，捕捉到更丰富的小涡结构。

表 1 本文与以往研究的数值结果比较

Table 1. Comparison of numerical results from previous studies in this paper

参数	来源	水力特性系数
Re	Study	${ { {\overline {C} }_{\text{D} } } }$	St
3900	NORBERG^[22]	0.98	0.215
	LYSENKO等^[23]: LES 和 TKE	0.97	0.209
	HANSEN 和 LONG^[24]	1.31	0.207
	MA等^[25]: DNS	−	0.219
	RAJANI等^[26]	1.100	0.200
	本文	1.210	0.210

下载: 导出CSV

| 显示表格

表 2 DNS和RANS数值方法对比

Table 2. Comparison of DNS and RANS numerical methods

工具	方法	精度	时间步长	时间步	计算时长/h
本文	DNS	6阶	0.001	100 000	6
Fluent	RANS	2阶	0.001	100 000	23
继表2
计算结果		涡量对比图
${ { { \overline {C} }_{ {\text{D}}} } }$	St	涡量对比图
1.210	0.210
1.217	0.193

下载: 导出CSV

| 显示表格

3 拦污栅水动力特性分析

3.1 数值模型

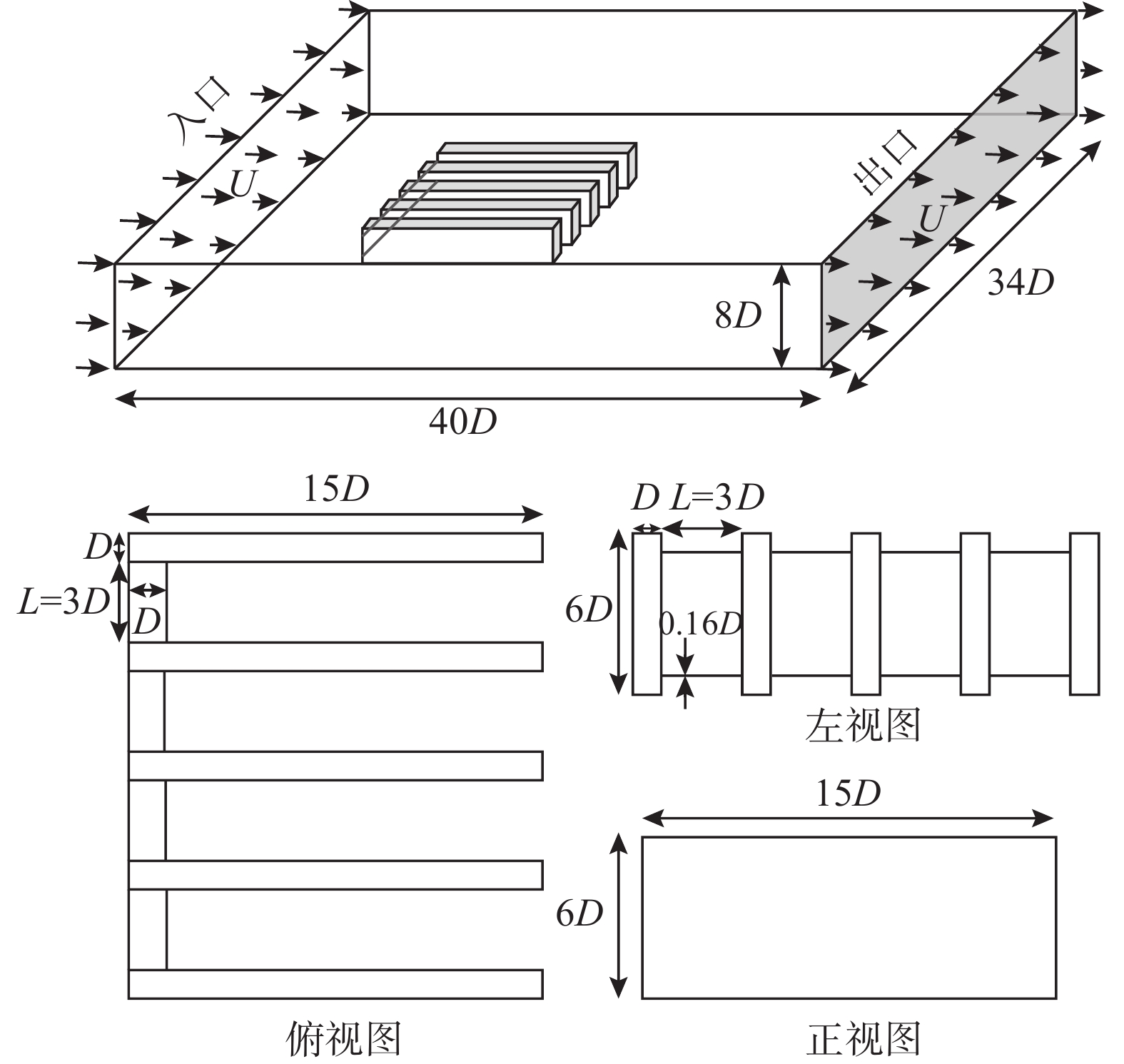
如图4所示，计算域的大小为L_x×L_y×L_z = 40D×34D×8D，污栅的中心坐标为(15D,17D,4D)。网格大小划分为 ${n_x} \times {n_y} \times {n_{\textit z}} = 712 \times 417 \times 64$ ， $\Delta t =$ $0.001$ 。力计算区域中心坐标与拦污栅的中心坐标一致，大小为长×宽×高= 20D×17D×6D。D为横栅条的宽度，也取为雷诺数计算的特征长度。

图 4 拦污栅几何尺寸及计算模型示意图

Figure 4. Geometric and calculation model of trash rack

下载: 全尺寸图片幻灯片

3.2 网格敏感性验证

在本小节中，通过五个不同的网格大小对网格敏感性进行验证。从表3可以看出，当网格大小大于n_x×n_y×n_z=708×410×60时，网格大小对计算结果的影响很小，为了节约计算时间以及计算成本，所以本文选择计算网格大小为n_x×n_y×n_z=712×417×64。

表 3 网格尺度对计算结果的影响

Table 3. Influence of grid size on calculation results

参数	长×宽×高	网格x×y×z	水力特性系数
Re	L_x×L_y×L_z	n_x×n_y×n_z	${ { { \overline {C} }_{ {\text{D}} } } }$	St
3900	40D×34D×8D	700×405×55	3.857	0.348
	40D×34D×8D	708×410×60	3.749	0.350
	40D×34D×8 D	712×417×64	3.758	0.352
	40D×34D×8D	715×420×70	3.758	0.353

下载: 导出CSV

| 显示表格

3.3 计算结果分析

3.3.1 雷诺数的影响

拦污栅在下游闸门启闭工作时，雷诺数会动态改变，通过改变雷诺数来近似模拟闸门启闭过程，分析拦污栅的水动力特性以及尾迹的变化规律。

表4为不同雷诺数下的拦污栅的水动力特性。从表4中可以看出，随着Re的增加，阻力系数和升力系数变化规律。斯特劳哈尔数St从0.0956增加到0.3517，增加了72.81%。这意味着涡脱落频率随Re的增加而增加。

表 4 不同雷诺数下的数值结果

Table 4. Numerical results with different Reynolds numbers

参数	水力特性系数
Re	${ \overline C_{\text{L}} } + C_{\text{L}}'$	${ \overline C_{\text{D}} } + C_{\text{D}}'$	St
200	0.000167±0.0000952	5.829±0.0115	0.096
500	0.011393±0.0126560	4.428±0.0201	0.154
800	0.021297±0.0317770	4.195±0.0357	0.172
1000	0.031009±0.0074590	4.165±0.0132	0.195
2000	0.032153±0.0092330	3.952±0.0132	0.270
3900	0.033817±0.0028717	3.758±0.0328	0.352

下载: 导出CSV

| 显示表格

图5展示了升阻力系数随时间的瞬态变化情况。从图5中可以看出，随着雷诺数的增加，时间平均阻力系数逐渐减小，从5.829(Re=200)降低到3.758(Re=3900)，减少了35.5%。升、阻力都呈现周期性变化规律，且St从0.0956(Re=200)增加到0.3517(Re=3900)，增加约3.5倍。同时也可看出，升力系数相对于阻力系数很小，对结构分析来说基本可以忽略。

图 5 阻力和升力系数随时间步变化规律

Figure 5. Resistance and lift coefficients over time

下载: 全尺寸图片幻灯片

图6为不同雷诺数下涡量的变化情况。从图6中可以看出，当Re=200时，由于流速低，在前缘和纵向栅条的两侧没有明显的流动分离现象。当Re=500时，最中间栅条两侧没有明显的涡结构分布，紧邻的两根栅条也只有靠近外侧有附着的近壁涡，主要由栅条前缘涡脱落产生。当雷诺数进一步增加时，每根栅条两侧都有明显的附着涡结构，并且前缘涡的分布范围明显增加，沿下游扩散的距离越远。同时也注意到，在不同雷诺数下，栅条尾缘涡结构也呈现完全不同的形态，雷诺数越大，涡脱落频率增加，涡尺度越小，脉动频率越高，这也是导致升、阻力频率随雷诺数增大的主要原因。同时前缘涡与尾缘涡的变化也是诱发不同雷诺数下升、阻力变化的主要流体动力因素。

图 6 涡量变化图

Figure 6. Vorticity diagram

下载: 全尺寸图片幻灯片

3.3.2 栅条间距的影响

栅条间距L是拦污栅在设计过程中的一个重要参考因素。在本节中，固定流动雷诺数为3900，栅条间距L从D~3D变化，来研究其对拦污栅水动力特性的影响。

从可以看出，随着L的增加，时间平均阻力系数 ${{{\overline {C}}_{{\text{D}}}}}$ 呈现逐渐微略降低的趋势，从3.968(L=D)下降到3.758(L=3D)，但阻力系数的频率呈逐渐增加的趋势，从0.242(L=D)上升到0.352(L=3D)。所以采用不同栅条间距是避免流激共振的一个重要工程措施之一，文献[27]也有类似结论。

表 5 不同栅条间距下的数值结果

Table 5. Numerical results with different fence spacing

参数	水力特性系数
L	${ { {\overline {C} }_{\text{D} } } } + C_{\rm{D}}'$	${ { { \overline {C} }_{\text{L} } } } + C_{\rm{L}}'$	St
D	3.968±0.0126	0.0257±0.0034	0.242
1.5D	3.947±0.0100	0.0250±0.0024	0.290
2.0D	3.847±0.0108	0.0232±0.0230	0.315
2.5D	3.793±0.0152	0.0285±0.0198	0.337
3.0D	3.758±0.03279	0.0338±0.00287	0.352

下载: 导出CSV

| 显示表格

图7显示了间距不同时拦污栅的涡量图。从图7中可以看出，间隔距离越大，流体能更容易流入栅条间隔中，在拦污栅头部以及中间栅条两侧的涡漩更易形成，而在间距较小时，流动在栅条之间的流动受阻，抑制了栅条中部段涡的生成，前缘流体向最上端和最下端的两侧扩展，导致栅条前缘产生较大的阻力。间距L越小时，各拦污栅纵向栅条尾部的涡区域越有聚合的趋势，栅条后的尾部涡之间明显相互干扰，涡的尺度变大，频率降低。而当L=3D 时，每个栅条后的尾部涡几乎独立存在，之间的相互干扰明显减弱。

图 7 不同栅条间距下拦污栅涡量图(Re=3900)

Figure 7. Vortex diagram at different fence spacing (Re=3900)

下载: 全尺寸图片幻灯片

图8为不同间距下的压力分布时均图，取自计算稳定后四个周期压力值的时间加权平均。由图可见，随着间距的增加，拦污栅头部的高压区压力值呈现逐渐减小的趋势，这也是阻力逐渐减小的主要原因。栅条尾部的压力以及栅条中间部分压力受栅条间距的影响相对较小。

图 8 不同栅条间距下拦污栅压力分布图(Re=3900)

Figure 8. Pressure distribution under different fence spacing (Re=3900)

下载: 全尺寸图片幻灯片

4 结论

基于高时空分辨率的Incompact3D开源软件构架，采用浸入边界法处理复杂流固边界，研究了拦污栅在中低流动雷诺数下(Re≤3900)的水动力特性，主要结论如下：

(1)在中低雷诺数流动下(Re≤3900)，随着雷诺数从200增加到3900，拦污栅的时间平均阻力系数降低了35.3%，漩涡脱落的频率从0.0956增加到0.3517。前缘涡与尾缘涡的变化是诱发不同雷诺数下升、阻力大小和频率变化的主要流体动力因素。

(2)在Re=3900时，随着栅条间距L=D增加到3D，时间平均阻力系数由3.968减小到3.758，但漩涡脱落频率呈现逐渐增加(0.242~0.352)的趋势。间距较小时，在栅条之间的流动受阻，前缘流体向最上端和最下端的两侧扩展，导致栅条前缘产生较大的阻力，并且拦污栅纵向栅条尾部的涡区域越有聚合的趋势，涡的尺度变大，频率降低。

(3)当闸门在启闭过程中，拦污栅结构将在中低雷诺数下工作，其水动力大小和频率随着雷诺数和栅条之间的间距而显著变化，即激振力和频率发生显著变化。研究成果对拦污栅结构在复杂服役条件下的优化设计和避免流激共振具有重要意义。

图 1 交错网格的二维变量排列

Figure 1. Two-dimensional variable arrangement of staggered (right) lattices

下载: 全尺寸图片幻灯片

图 2 力计算的控制体积示意图

Figure 2. Schematic diagram of the control volume for force calculation

下载: 全尺寸图片幻灯片

图 3 计算域的示意图

Figure 3. Schematic diagram of the calculation domain

下载: 全尺寸图片幻灯片

图 4 拦污栅几何尺寸及计算模型示意图

Figure 4. Geometric and calculation model of trash rack

下载: 全尺寸图片幻灯片

图 5 阻力和升力系数随时间步变化规律

Figure 5. Resistance and lift coefficients over time

下载: 全尺寸图片幻灯片

图 6 涡量变化图

Figure 6. Vorticity diagram

下载: 全尺寸图片幻灯片

图 7 不同栅条间距下拦污栅涡量图(Re=3900)

Figure 7. Vortex diagram at different fence spacing (Re=3900)

下载: 全尺寸图片幻灯片

图 8 不同栅条间距下拦污栅压力分布图(Re=3900)

Figure 8. Pressure distribution under different fence spacing (Re=3900)

下载: 全尺寸图片幻灯片

表 1 本文与以往研究的数值结果比较

Table 1 Comparison of numerical results from previous studies in this paper

参数	来源	水力特性系数
Re	Study	${ { {\overline {C} }_{\text{D} } } }$	St
3900	NORBERG^[22]	0.98	0.215
	LYSENKO等^[23]: LES 和 TKE	0.97	0.209
	HANSEN 和 LONG^[24]	1.31	0.207
	MA等^[25]: DNS	−	0.219
	RAJANI等^[26]	1.100	0.200
	本文	1.210	0.210

下载: 导出CSV

表 2 DNS和RANS数值方法对比

Table 2 Comparison of DNS and RANS numerical methods

工具	方法	精度	时间步长	时间步	计算时长/h
本文	DNS	6阶	0.001	100 000	6
Fluent	RANS	2阶	0.001	100 000	23
继表2
计算结果		涡量对比图
${ { { \overline {C} }_{ {\text{D}}} } }$	St	涡量对比图
1.210	0.210
1.217	0.193

下载: 导出CSV

表 3 网格尺度对计算结果的影响

Table 3 Influence of grid size on calculation results

参数	长×宽×高	网格x×y×z	水力特性系数
Re	L_x×L_y×L_z	n_x×n_y×n_z	${ { { \overline {C} }_{ {\text{D}} } } }$	St
3900	40D×34D×8D	700×405×55	3.857	0.348
	40D×34D×8D	708×410×60	3.749	0.350
	40D×34D×8 D	712×417×64	3.758	0.352
	40D×34D×8D	715×420×70	3.758	0.353

下载: 导出CSV

表 4 不同雷诺数下的数值结果

Table 4 Numerical results with different Reynolds numbers

参数	水力特性系数
Re	${ \overline C_{\text{L}} } + C_{\text{L}}'$	${ \overline C_{\text{D}} } + C_{\text{D}}'$	St
200	0.000167±0.0000952	5.829±0.0115	0.096
500	0.011393±0.0126560	4.428±0.0201	0.154
800	0.021297±0.0317770	4.195±0.0357	0.172
1000	0.031009±0.0074590	4.165±0.0132	0.195
2000	0.032153±0.0092330	3.952±0.0132	0.270
3900	0.033817±0.0028717	3.758±0.0328	0.352

下载: 导出CSV

表 5 不同栅条间距下的数值结果

Table 5 Numerical results with different fence spacing

参数	水力特性系数
L	${ { {\overline {C} }_{\text{D} } } } + C_{\rm{D}}'$	${ { { \overline {C} }_{\text{L} } } } + C_{\rm{L}}'$	St
D	3.968±0.0126	0.0257±0.0034	0.242
1.5D	3.947±0.0100	0.0250±0.0024	0.290
2.0D	3.847±0.0108	0.0232±0.0230	0.315
2.5D	3.793±0.0152	0.0285±0.0198	0.337
3.0D	3.758±0.03279	0.0338±0.00287	0.352

下载: 导出CSV

参考文献(27)

[1]	李子民. 基于振型分解反应谱法的水电站进水口拦污栅墩结构抗震特性研究[D]. 西安: 西安理工大学, 2019. LI Zimin. Study on seismic behavior of the spillway pier structure of the intake of hydropower station project based on vibration mode decomposition spectrum method [D]. Xi’an: Xi’an University of Technology, 2019. (in Chinese)
[2]	王秋绎. 拦污栅栅条流场特征和共振分析[D]. 大连: 大连理工大学, 2020. WANG Qiuyi. The flow field characteristics and resonance analysis of trash-rack bars [D]. Dalian: Dalian University of Technology, 2020. (in Chinese)
[3]	仇宝云, 刘地, 袁连冲, 等. 泵站漂浮物拦污栅拦截与过栅试验研究[J]. 排灌机械工程学报, 2022, 40(6): 582 − 587. QIU Baoyun, LIU Di, YUAN Lianchong, et al. Experimental study on floating objects being intercepted by and passing trash racks in pumping station [J]. Journal of Drainage and Irrigation Machinery Engineering, 2022, 40(6): 582 − 587. (in Chinese)
[4]	WALCZAK N, WALCZAK Z, TYMIŃSKI T. Laboratory research on hydraulic losses on SHP inlet channel trash racks [J]. Energies, 2022, 15(20): 7602. doi: 10.3390/en15207602
[5]	ZAYED M, FAROUK E. Effect of blocked trash rack on open channel infrastructure [J]. Water Practice and Technology, 2021, 16(1): 247 − 262. doi: 10.2166/wpt.2020.110
[6]	李春光, 陈政清, 张记. 主动格栅紊流场对典型主梁颤振导数影响的研究[J]. 实验力学, 2016, 31(1): 75 − 86. LI Chunguang, CHEN Zhengqing, ZHANG Ji. On the Influence of active grid turbulence field on flutter derivatives of typical main girder [J]. Journal of Experimental Mechanics, 2016, 31(1): 75 − 86. (in Chinese)
[7]	黄睿, 张庆河, 张金凤, 等. 双层横向振荡格栅紊流特性的实验研究[J]. 水动力学研究与进展A辑, 2022, 37(2): 244 − 251. HUANG Rui, ZHANG Qinghe, ZHANG Jinfeng, et al. Experimental research on turbulence characteristics of double layer transverse oscillating grid [J]. Chinese Journal of Hydrodynamics A, 2022, 37(2): 244 − 251. (in Chinese)
[8]	肖金龙. 振荡格栅紊流与泥沙相互作用的实验研究[D]. 天津: 天津大学, 2013. XIAO Jinlong. Experimental study of particle-fluid interactions in oscillating grid generated turbulence [D]. Tianjin: Tianjin University, 2013. (in Chinese)
[9]	MILTENOVIC A, PRODANOVIĆ M, BEJU L, et al. Innovative solution of fine horizontal trash rack for small hydroelectric power stations [J]. IOP Conference Series: Materials Science and Engineering, 2019, 659(1): 012049. doi: 10.1088/1757-899X/659/1/012049
[10]	LATIF M A, SARWAR M K, FAROOQ R, et al. Estimating energy efficient design parameters for trash racks at low head hydropower stations [J]. Water, 2022, 14(17): 2609. doi: 10.3390/w14172609
[11]	LUČIN I, ČARIJA Z, GRBČIĆ L, et al. Assessment of head loss coefficients for water turbine intake trash-racks by numerical modeling [J]. Journal of Advanced Research, 2020, 21: 109 − 119. doi: 10.1016/j.jare.2019.10.010
[12]	高学平, 袁野, 刘殷竹, 等. 拦污栅结构对进出水口水力特性影响试验研究[J]. 水力发电学报, 2023, 42(2): 74 − 86. doi: 10.13465/j.cnki.jvs.2014.21.023 Gao Xueping, Yuan Ye, Liu Yinzhu et al. Experimental study on effect of trash rack structure on hydraulic characteristics of inlet and outlet [J]. Journal of Hydroelectric Engineering, 2023, 42(2): 74 − 86. (in Chinese) doi: 10.13465/j.cnki.jvs.2014.21.023
[13]	WANG W Q, WANG J L, CUI G Z, et al. A numerical study on elliptical particle deposition with an immersed boundary-lattice Boltzmann method [J]. Computers & Fluids, 2022, 246: 105644.
[14]	郭涛, 张纹惠, 王文全, 等. 基于IBM法的低雷诺数下涡激振动高质量比效应的研究[J]. 工程力学, 2022, 39(3): 222 − 232. doi: 10.6052/j.issn.1000-4750.2021.07.0566 GUO Tao, ZHANG Wenhui, WANG Wenquan, et al. Effects of high mass and damping ratio on VIV of a circular cylinder with low Reynolds number based on IBM [J]. Engineering Mechanics, 2022, 39(3): 222 − 232. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.07.0566
[15]	王文全, 张国威, 闫妍. 模拟复杂流动的一种隐式直接力浸入边界方法[J]. 工程力学, 2017, 34(2): 28 − 33, 93. doi: 10.6052/j.issn.1000-4750.2015.07.0600 WANG Wenquan, ZHANG Guowei, YAN Yan. An implicit direct force immersed boundary method for simulating complex flow [J]. Engineering Mechanics, 2017, 34(2): 28 − 33, 93. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.07.0600
[16]	LAIZET S, LAMBALLAIS E. High-order compact schemes for incompressible flows: A simple and efficient method with quasi-spectral accuracy [J]. Journal of Computational Physics, 2009, 228(16): 5989 − 6015. doi: 10.1016/j.jcp.2009.05.010
[17]	罗灿炎, 毕林, 徐晶磊, 等. 笛卡尔网格下不同湍流模型的壁面函数方法研究[J]. 工程力学, 2024, 41(8): 11 − 22. doi: 10.6052/j.issn.1000-4750.2022.06.0558 LUO Canyan, BI Lin, XU Jinglei, et al. Study on wall function method of different turbulence models based on Cartesian grid [J]. Engineering Mechanics, 2024, 41(8): 11 − 22. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.06.0558
[18]	GRONSKIS A, ARTANA G. A simple and efficient direct forcing immersed boundary method combined with a high order compact scheme for simulating flows with moving rigid boundaries [J]. Computers & Fluids, 2016, 124: 86 − 104.
[19]	LELE S K. Compact finite difference schemes with spectral-like resolution [J]. Journal of Computational Physics, 1992, 103(1): 16 − 42. doi: 10.1016/0021-9991(92)90324-R
[20]	叶康生, 孟令宁. 二维泊松方程问题Lagrange型有限元p型超收敛算法[J]. 工程力学, 2022, 39(2): 23 − 36. doi: 10.6052/j.issn.1000-4750.2020.12.0934 YE Kangsheng, MENG Lingning. A p-type superconvergent recovery method for Fe analysis with lagrange elements on two-dimensional Poisson equations [J]. Engineering Mechanics, 2022, 39(2): 23 − 36. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0934
[21]	黄泽敏, 袁驷. 二维有限元单元角结点位移精度修正之初探[J]. 工程力学, 2021, 38(增刊 1): 1 − 6. doi: 10.6052/j.issn.1000-4750.2020.07.S002 HUANG Zemin, YUAN Si. A preliminary study on accuracy improvement of nodal displacements in 2D finite element method [J]. Engineering Mechanics, 2021, 38(Suppl 1): 1 − 6. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.S002
[22]	NORBERG C. Effects of Reynolds number and low-intensity freestream turbulence on the flow around a circular cylinder [R]. Gothenburg, Sweden: Chalmers University of Technology, 1987: 1 − 55.
[23]	LYSENKO D A, ERTESVÅG I S, RIAN K E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFOAM toolbox [J]. Flow, Turbulence and Combustion, 2012, 89(4): 491 − 518. doi: 10.1007/s10494-012-9405-0
[24]	HANSEN R, LONG L. Large-eddy simulation of a circular cylinder on unstructured grids [C]// 40th AIAA Aerospace Sciences Meeting & Exhibit. Reno: AIAA, 2002: 982.
[25]	MA X, KARAMANOS G S, KARNIADAKIS G E. Dynamics and low-dimensionality of a turbulent near wake [J]. Journal of Fluid Mechanics, 2000, 410: 29 − 65. doi: 10.1017/S0022112099007934
[26]	RAJANI B N, KANDASAMY A, MAJUMDAR S. LES of flow past circular cylinder at Re=3900 [J]. Journal of Applied Fluid Mechanics, 2016, 9(3): 1421 − 1435. doi: 10.18869/acadpub.jafm.68.228.24178
[27]	祁林攀, 辛勇军, 李岗. 水电站拦污栅结构动力特性及抗振研究综述[J]. 人民黄河, 2013, 35(11): 87 − 89, 92. doi: 10.3969/j.issn.1000-1379.2013.11.031 QI Linpan, XIN Yongjun, LI Gang. Analysis on dynamic characteristic and anti-vibration design of trash rack of hydropower station [J]. Yellow River, 2013, 35(11): 87 − 89, 92. (in Chinese) doi: 10.3969/j.issn.1000-1379.2013.11.031

施引文献

资源附件(0)

图(8) / 表(5)

计量

文章访问数: 166
HTML全文浏览量: 58
PDF下载量: 27
被引次数: 0

1 控制方程与数值方法
1.1 控制方程
1.2 数值方法
1.2.1 时间推进
1.2.2 对流项和粘性项处理
1.2.3 压力项处理
1.2.4 力的计算
2 验证算例
3 拦污栅水动力特性分析
3.1 数值模型
3.2 网格敏感性验证
3.3 计算结果分析
3.3.1 雷诺数的影响
3.3.2 栅条间距的影响
4 结论

1 控制方程与数值方法
1.1 控制方程
1.2 数值方法
1.2.1 时间推进
1.2.2 对流项和粘性项处理
1.2.3 压力项处理
1.2.4 力的计算
2 验证算例
3 拦污栅水动力特性分析
3.1 数值模型
3.2 网格敏感性验证
3.3 计算结果分析
3.3.1 雷诺数的影响
3.3.2 栅条间距的影响
4 结论

参考文献(27)

施引文献

资源附件(0)

中低雷诺数下拦污栅结构动态绕流数值模拟

作者简介: 杨家富(2000−)，男，四川叙州人，硕士生，主要从事流体力学方面的研究(E-mail: 254207814@qq.com) 骆佳玲(1997−)，女，湖南岳阳人，博士生，主要从事流体力学方面的研究(E-mail: 244210807@qq.com)

通讯作者: 王文全(1977−)，男，四川南充人，教授，博士，博导，主要从事多场耦合力学方面的研究(E-mail: wwqquan@126.com)

计量

出版历程

NUMERICAL SIMULATION OF THE FLOW CHARACTERISTICS AROUND A TRASH RACK AT LOW AND MEDIUM REYNOLDS NUMBER

1 控制方程与数值方法

1.1 控制方程

1.2 数值方法

1.2.1 时间推进

1.2.2 对流项和粘性项处理

1.2.3 压力项处理

1.2.4 力的计算

2 验证算例

3 拦污栅水动力特性分析

3.1 数值模型

3.2 网格敏感性验证

3.3 计算结果分析

3.3.1 雷诺数的影响

3.3.2 栅条间距的影响

4 结论

计量

出版历程

目录

1 控制方程与数值方法

1.1 控制方程

1.2 数值方法

1.2.1 时间推进

1.2.2 对流项和粘性项处理

1.2.3 压力项处理

1.2.4 力的计算

2 验证算例

3 拦污栅水动力特性分析

3.1 数值模型

3.2 网格敏感性验证

3.3 计算结果分析

3.3.1 雷诺数的影响

3.3.2 栅条间距的影响

4 结论

作者简介:
杨家富(2000−)，男，四川叙州人，硕士生，主要从事流体力学方面的研究(E-mail: 254207814@qq.com)

骆佳玲(1997−)，女，湖南岳阳人，博士生，主要从事流体力学方面的研究(E-mail: 244210807@qq.com)

通讯作者:
王文全(1977−)，男，四川南充人，教授，博士，博导，主要从事多场耦合力学方面的研究(E-mail: wwqquan@126.com)