高压铸铝合金本构模型和断裂准则研究

张明辉; 魏广凯; 李伦操; 杨斌; 付昆昆

doi:10.6052/j.issn.1000-4750.2022.12.1073

高压铸铝合金本构模型和断裂准则研究

同济大学航空航天与力学学院，上海 200082

基金项目: 国家自然科学基金项目(12172257)；国家自然科学基金青年项目(12102303)

详细信息

作者简介:
张明辉(1993−)，男，河南人，博士生，主要从事增材制造的力学性能研究(E-mail: zhangminghui_edu@163.com)

魏广凯(1996−)，男，山东人，博士生，主要从事复合材料结构设计研究(E-mail: youthwgk@163.com)

李伦操(1995−)，男，山东人，博士生，主要从事流体力学研究(E-mail: liluncao@tongji.edu.cn)

杨　斌(1988−)，男，湖北人，助理教授，博士，主要从事工程结构损伤分析研究(E-mail: yangbin2018@tongji.edu.cn)

通讯作者:
付昆昆(1984−)，男，黑龙江人，教授，博士，博导，主要从事复合材料的损伤评估、防护及增材制造研究(E-mail: 1984fukunkun@tongji.edu.cn)

中图分类号: TG115.5；U465.2+2
计量
- 文章访问数: 486
- HTML全文浏览量: 70
- PDF下载量: 119
出版历程
- 收稿日期: 2022-12-13
- 修回日期: 2023-03-06
- 网络出版日期: 2023-04-06
- 刊出日期: 2025-04-24

STUDY ON CONSTITUTIVE MODEL AND FRACTURE CRITERION OF HIGH PRESSURE CAST ALUMINUM ALLOY

School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200082, China

摘要

摘要:
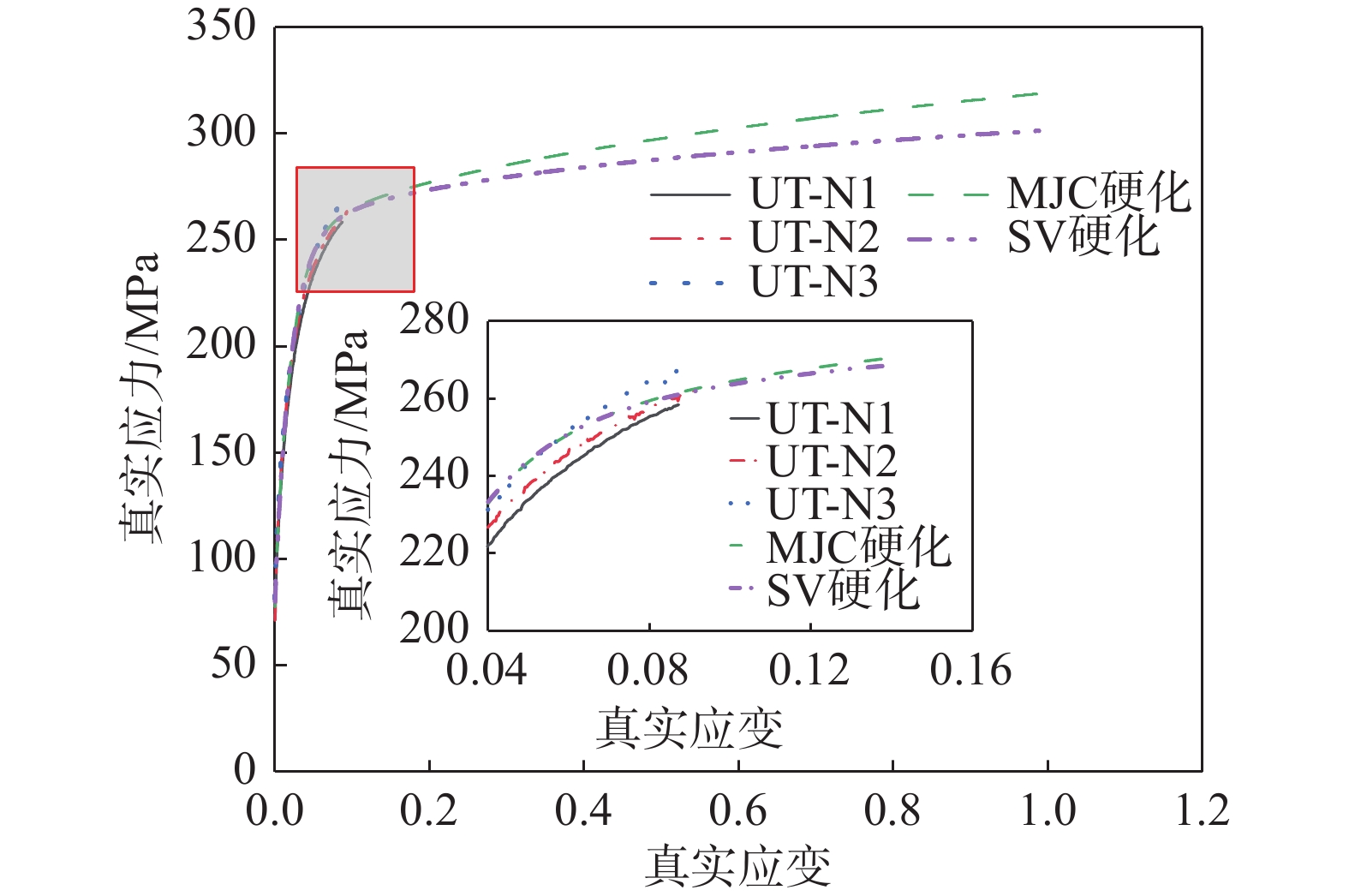
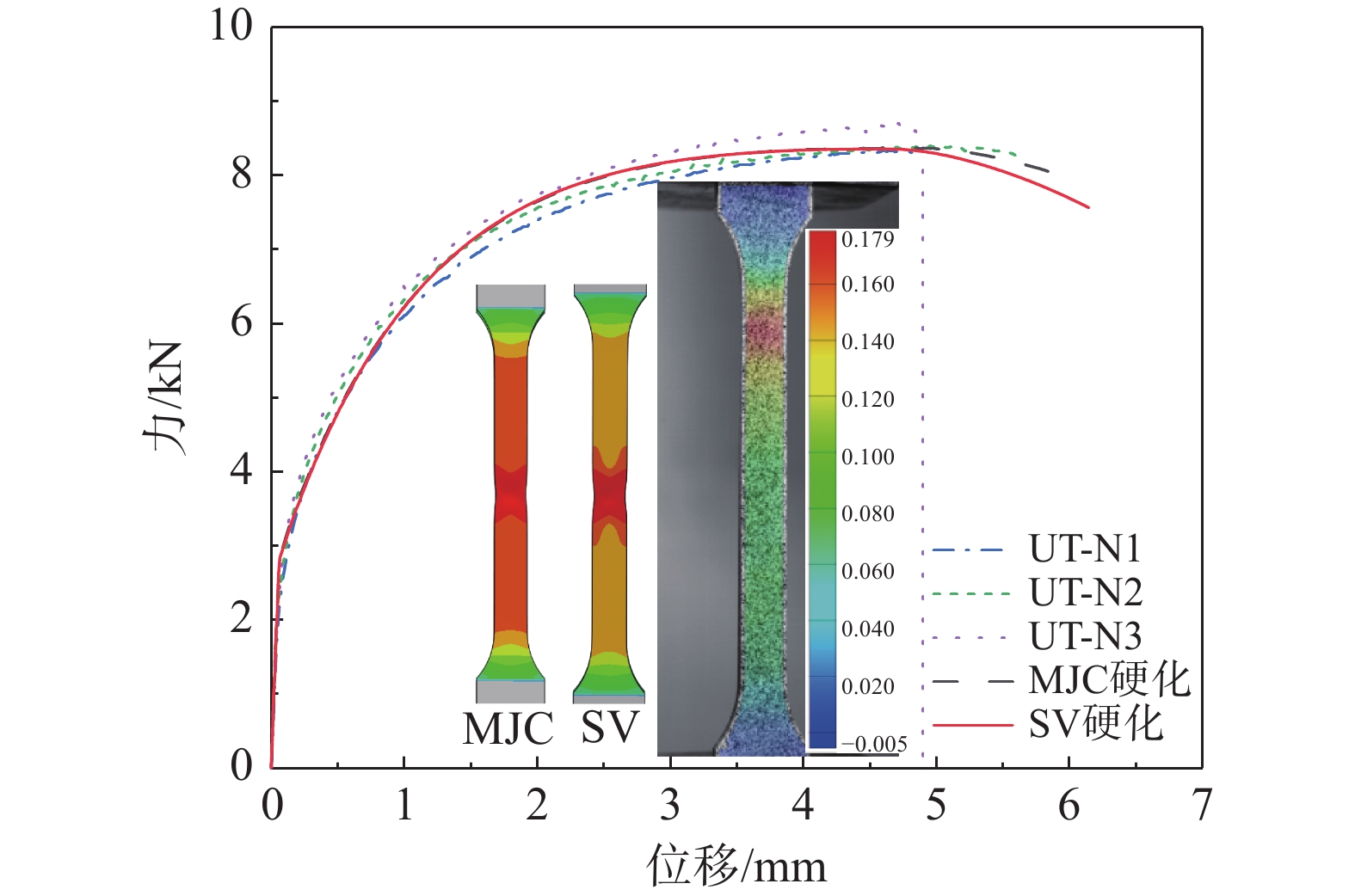
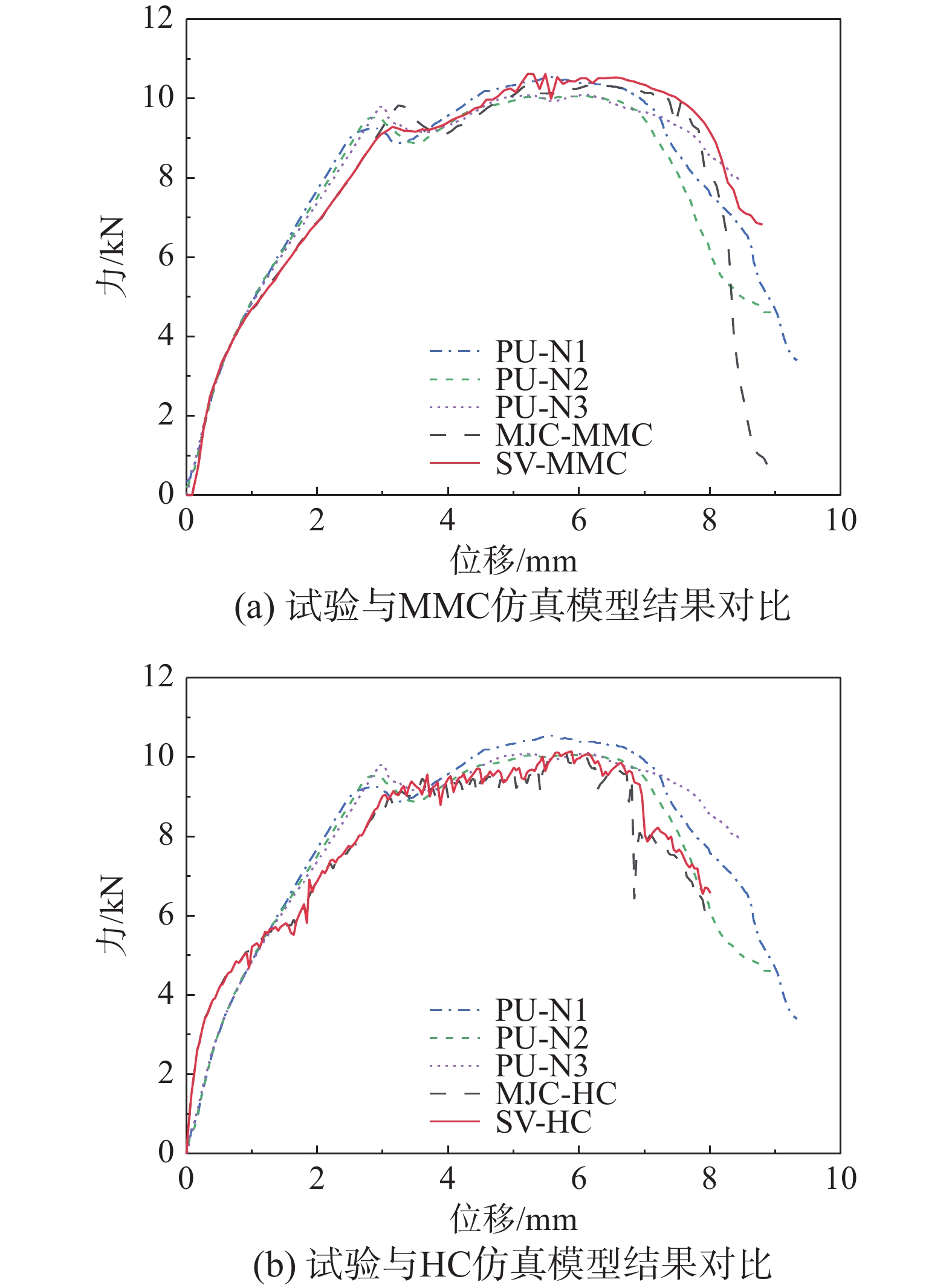
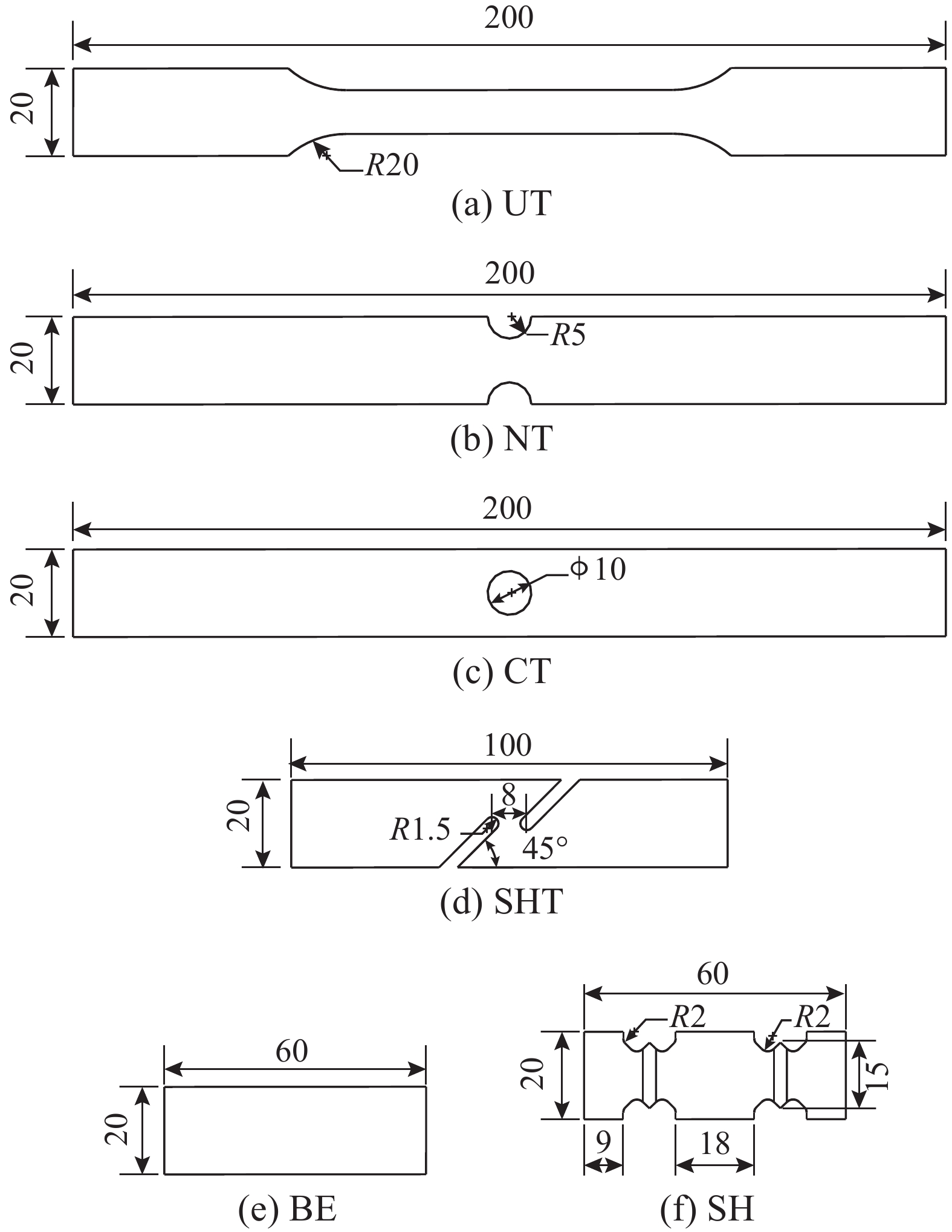
高压铸铝合金是实现结构轻量化最常用的轻质合金材料之一，其本构关系和断裂准则是结构安全性设计的关键。为了探索高压铸造铝合金ZTHJ01在准静态下的本构模型和断裂准则，设计了高压铸造铝合金标准拉伸、R5缺口拉伸、中心孔拉伸、平面剪切、蝴蝶剪切和三点弯曲六种实验样件，结合数字图像相关法(Digital Image Correction, DIC)开展了试验测试。根据对应力-应变曲线外推两种不同混合性硬化准则，准确描述了高压铸铝合金的应变硬化特性。提出有限元仿真模型，获得了不同应力状态下断裂应变与应力三轴度和Lode角参数的相互关系，构建并标定了修正的Mohr-Coulomb断裂准则和Hosford-Coulomb断裂准则参数。通过杯突试验和有限元仿真模拟验证了不同硬化准则下断裂模型的有效性。结果表明：两种不同硬化准则下的修正Mohr-Coulomb和Hosford-Coulomb断裂准则都可较好的实现对高压铸铝合金断裂失效的准确预测，其中，Swift-Voce硬化准则下的修正Mohr-Coulomb断裂模型表现出更高的精度。
- 高压铸铝 /
- 本构模型 /
- 修正Mohr-Coulomb断裂准则 /
- Hosford-Coulomb断裂准则 /
- 数值模拟
Abstract:
High pressure cast aluminum alloy is one of the most commonly used lightweight alloy materials to realize structural lightweight. Its constitutive relation and fracture criterion are key to structural safety design. To explore the constitutive model and fracture criterion of high-pressure casting aluminum alloy ZTHJ01 under quasi-static state, six experimental specimens of high-pressure casting aluminum alloy, including standard tensile, R5 notch tensile, central hole tensile, plane shear, butterfly shear and three-point bending, were designed and tested in combination with Digital Image Correction (DIC). According to the stress-strain curve, two different mixed hardening criteria are extrapolated, and the strain hardening characteristics of high-pressure cast aluminum alloy are accurately described. The finite element simulation model is proposed, and the relationship between fracture strain and stress triaxiality and Lode angle parameters under different stress states is obtained. The Modified Mohr-Coulomb (MMC) fracture criterion and Hosford-Coulomb (HC) fracture criterion parameters are constructed and calibrated. The effectiveness of the fracture model under different hardening criteria is verified by cupping test and finite element simulation. The results show that the MMC and HC fracture criteria under two different hardening criteria can better predict the fracture failure of high-pressure cast aluminum alloy, and the MMC fracture model under swift voce hardening criteria shows higher accuracy.
- high pressure cast aluminum /
- constitutive model /
- MMC fracture criterion /
- HC fracture criterion /
- numerical simulation

HTML全文

图 1 不同应力下铝合金材料试验样件　/mm

Figure 1. Aluminum alloy material test sample under different stress

下载: 全尺寸图片幻灯片

图 2 力学性能试验和DIC测试设备

Figure 2. The equipment of mechanical property and DIC

下载: 全尺寸图片幻灯片

图 3 应力-应变试验数据及混合硬化外推曲线

Figure 3. Stress strain test data and mixed hardening extrapolation curve

下载: 全尺寸图片幻灯片

图 4 试验与仿真的力-位移曲线对比图

Figure 4. Comparison of force displacement curve between test and simulation

下载: 全尺寸图片幻灯片

图 5 不同应力状态下试验与仿真力-位移曲线对比图

Figure 5. Comparison of force displacement curves of test and simulation under different stress states

下载: 全尺寸图片幻灯片

图 6 应力三轴度和Lode角参数与等效塑性应变演变过程

Figure 6. Evolution of stress triaxiality and Lode angle parameters relative to equivalent plastic strain

下载: 全尺寸图片幻灯片

图 7 不同材料本构模型下MMC断裂模型

Figure 7. MMC fracture model under different constitutive models of materials

下载: 全尺寸图片幻灯片

图 8 不同本构模型下MMC仿真模型与试验结果对比

Figure 8. Comparison of MMC simulation model and test results under different constitutive models

下载: 全尺寸图片幻灯片

图 9 不同材料本构模型下HC断裂模型

Figure 9. HC fracture model under different constitutive models of materials

下载: 全尺寸图片幻灯片

图 10 不同本构模型下HC仿真模型与试验结果对比

Figure 10. Comparison between HC simulation model and test results under different constitutive models

下载: 全尺寸图片幻灯片

图 11 杯突试验仿真模型示意图

Figure 11. Schematic diagram of cupping test simulation model

下载: 全尺寸图片幻灯片

图 12 杯突试验仿真结果与试验结果对比图

Figure 12. Comparison between simulation results and test results of cupping test

下载: 全尺寸图片幻灯片

图 13 杯突试验仿真结果与失效样件对比图

Figure 13. Comparison between simulation results of cupping test and failure samples

下载: 全尺寸图片幻灯片

表 1 两种混合型硬化准则参数

Table 1 Two mixed hardening criterion parameters

符号	A	B	C	Q	${\varepsilon _0}$
值	77.55	523.48	528.82	183.75	0.00175

符号	$\beta$	n₁	n₂	${\alpha _1}$	${\alpha _2}$
值	48.54	0.3983	0.2705	0.17	0.15

下载: 导出CSV

表 2 不同应力状态下的断裂应变、应力三轴度和Lode角参数

Table 2 Fracture strain, stress triaxiality and Lode angle parameters under different stress states

样件类型	MJC本构			SV本构
样件类型	应力三轴度 $\overline \eta$	Lode参数 $\overline \theta$	断裂应变 ${\overline \varepsilon _{\rm{f}}}$	应力三轴度 $\overline \eta$	Lode参数 $\overline \theta$	断裂应变 ${\overline \varepsilon _{\rm{f}}}$
UT	0.335 01	0.995 59	0.113 65	0.341 35	0.981 56	0.141 80
NT	0.347 95	0.895 61	0.172 81	0.347 47	0.892 65	0.174 22
CT	0.378 52	0.988 75	0.154 89	0.378 87	0.988 24	0.154 33
BE	0.565 47	0.039 33	0.185 47	0.565 95	0.038 75	0.189 22
SHT	0.497 75	0.951 99	0.185 53	0.498 56	0.949 60	0.186 40
SH	−0.040 22	−0.102 14	0.313 38	−0.041 60	−0.100 89	0.331 90

下载: 导出CSV

表 3 不同材料本构模型下MMC断裂模型

Table 3 MMC fracture model under different constitutive models of materials

本构	拟合参数 ${c_1}$	拟合参数 ${c_2}$	拟合参数 $c_\theta ^c$	拟合参数 $c_\theta ^s$	拟合优度
MJC	0.1177	180.2	0.8292	0.8162	0.8513
SV	0.1336	185.9	0.8600	0.8279	0.9182

下载: 导出CSV

表 4 不同材料本构模型下HC断裂模型

Table 4 HC fracture model under different constitutive models of materials

本构	拟合参数a	拟合参数b	拟合参数c	拟合参数n	拟合优度
MJC	2	0.006243	0.03760	0.1	0.7495
SV	2	0.006541	0.03888	0.1	0.8583

下载: 导出CSV

参考文献(44)

[1]	赖兴华, 王磊, 李洁, 等. 铝型材防撞梁的碰撞断裂失效表征[J]. 清华大学学报(自然科学版), 2017, 57(5): 504 − 510. LAI Xinghua, WANG Lei, LI Jie, et al. Characterization of the fracture of an aluminum alloy anticollision-beam to impact loading [J]. Journal of Tsinghua University (Science and Technology), 2017, 57(5): 504 − 510. (in Chinese)
[2]	张俊超, 钟鼓, 邹纯, 等. 高真空压铸铝合金的研究进展[J]. 材料导报, 2018, 32(增刊 2): 375 − 378. ZHANG Junchao, ZHONG Gu, ZOU Chun, et al. Research progress of the high vacuum die-casting aluminum alloys [J]. Materials Reports, 2018, 32(Suppl 2): 375 − 378. (in Chinese)
[3]	NIU Z C, LIU G Y, LI T, et al. Effect of high pressure die casting on the castability, defects and mechanical properties of aluminium alloys in extra-large thin-wall castings [J]. Journal of Materials Processing Technology, 2022, 303: 117525. doi: 10.1016/j.jmatprotec.2022.117525
[4]	JOLLY M, KATGERMAN L. Modelling of defects in aluminium cast products [J]. Progress in Materials Science, 2022, 123: 100824. doi: 10.1016/j.pmatsci.2021.100824
[5]	杨卓云, 赵长财, 董国疆, 等. 基于Lou-2013韧性断裂准则5182铝板成形极限研究[J]. 机械工程学报, 2019, 55(16): 47 − 57. doi: 10.3901/JME.2019.16.047 YANG Zhuoyun, ZHAO Changcai, DONG Guojiang, et al. Forming limit research of 5182 aluminum alloy sheet based on Lou-2013 ductile fracture criterion [J]. Journal of Mechanical Engineering, 2019, 55(16): 47 − 57. (in Chinese) doi: 10.3901/JME.2019.16.047
[6]	DONG G J, ZHAO C C, PENG Y X, et al. Hot granules medium pressure forming process of AA7075 conical parts [J]. Chinese Journal of Mechanical Engineering, 2015, 28(3): 580 − 591. doi: 10.3901/CJME.2015.0217.019
[7]	叶继红, 范志鹏. 基于微观机制的复杂应力状态下钢材韧性断裂行为研究[J]. 工程力学, 2021, 38(5): 38 − 49. doi: 10.6052/j.issn.1000-4750.2020.06.0394 YE Jihong, FANG Zhipeng. Ductile fracture behavior of steel under complexstress state based on microscopic mechanism [J]. Engineering Mechanics, 2021, 38(5): 38 − 49. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0394
[8]	钱凌云, 纪婉婷, 王小灿, 等. 不同应力状态下的高强钢板断裂机理及预测[J]. 机械工程学报, 2020, 56(24): 72 − 80. doi: 10.3901/JME.2020.24.072 QIAN Lingyun, JI Wanting, WANG Xiaocan, et al. Research on fracture mechanism and prediction of high-strength steel sheet under different stress states [J]. Journal of Mechanical Engineering, 2020, 56(24): 72 − 80. (in Chinese) doi: 10.3901/JME.2020.24.072
[9]	ZHANG Y F, SHEN F H, ZHENG J, et al. Ductility prediction of HPDC aluminum alloy using a probabilistic ductile fracture model [J]. Theoretical and Applied Fracture Mechanics, 2022, 119: 103381. doi: 10.1016/j.tafmec.2022.103381
[10]	YANG Z Y, ZHAO C C, DONG G J, et al. Experimental calibration of ductile fracture parameters and forming limit of AA7075-T6 sheet [J]. Journal of Materials Processing Technology, 2021, 291: 117044. doi: 10.1016/j.jmatprotec.2021.117044
[11]	YANG B, LI Y, FU K K. In-plane impact-induced elastic buckling behaviour of rectangular transversally isotropic stiffened plates with all edges elastically restrained against rotation [J]. International Journal of Mechanical Sciences, 2020, 174: 105478. doi: 10.1016/j.ijmecsci.2020.105478
[12]	ZHANG M H, HU G Q, LIU X T, et al. An improved strength degradation model for fatigue life prediction considering material characteristics [J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43(5): 1 − 12. doi: 10.1007/s40430-021-02997-4
[13]	JIANG C J, LIU X T, ZHANG M H, et al. An improved nonlinear cumulative damage model for strength degradation considering loading sequence [J]. International Journal of Damage Mechanics, 2021, 30(3): 415 − 430. doi: 10.1177/1056789520964860
[14]	马宏越, 肖纳敏, 钱鹏, 等. 非耦合韧性断裂准则及其在航空金属材料中的应用[J]. 航空材料学报, 2021, 41(2): 16 − 31. doi: 10.11868/j.issn.1005-5053.2020.000134 MA Hongyue, XIAO Namin, QIAN Peng, et al. Uncoupled ductile fracture criterion and its application in aeronautical metallic materials [J]. Journal of Aeronautical Materials, 2021, 41(2): 16 − 31. (in Chinese) doi: 10.11868/j.issn.1005-5053.2020.000134
[15]	GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part I—yield criteria and flow rules for porous ductile media [J]. Journal of Engineering Materials and Technology, 1977, 99(1): 2 − 15. doi: 10.1115/1.3443401
[16]	董建鹏, 王时龙, 周杰, 等. 基于修正GTN模型的不锈钢管剪切过程韧性断裂准则研究[J]. 工程力学, 2021, 38(3): 239 − 247. doi: 10.6052/j.issn.1000-4750.2020.05.0303 DONG Jianpeng, WANG Shilong, ZHOU Jie, et al. The ductile fracture criterion of stainless-steel tubes in the shearing process based on modified GTN model [J]. Engineering Mechanics, 2021, 38(3): 239 − 247. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.0303
[17]	XIAO J Y, WANG G Z, WANG Y H, et al. Two-parameter fracture prediction for cracked plates under bending [J]. Engineering Fracture Mechanics, 2021, 255: 107974. doi: 10.1016/j.engfracmech.2021.107974
[18]	卓子超, 张庆亚, 王江超. 船板钢焊接接头的断裂失效行为及GTN模型的数值分析[J]. 工程力学, 2020, 37(11): 238 − 247. doi: 10.6052/j.issn.1000-4750.2019.12.0746 ZHUO Zichao, ZHANG Qingya, WANG Jiangchao. Fracture behavior of welded joints of ship steel plates and numerical analysis with gtn model [J]. Engineering Mechanics, 2020, 37(11): 238 − 247. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.12.0746
[19]	TENG B G, WANG W N, XU Y C. Ductile fracture prediction in aluminium alloy 5A06 sheet forming based on GTN damage model [J]. Engineering Fracture Mechanics, 2017, 186: 242 − 254. doi: 10.1016/j.engfracmech.2017.10.014
[20]	COCKROFT M G, LATHAM D J. Ductility and the workability of metals [J]. Journal of the Institute of Metals, 1968, 96(2): 33 − 39.
[21]	RICE J R, TRACEY D M. On the ductile enlargement of voids in triaxial stress fields [J]. Journal of the Mechanics and Physics of Solids, 1969, 17(3): 201 − 217. doi: 10.1016/0022-5096(69)90033-7
[22]	OH S I, CHEN C C, KOBAYASHI S. Ductile fracture in axisymmetric extrusion and drawing—part 2: Workability in extrusion and drawing [J]. Journal of Engineering for Industry, 1979, 101(1): 36 − 44. doi: 10.1115/1.3439471
[23]	JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31 − 48. doi: 10.1016/0013-7944(85)90052-9
[24]	苏康, 白瑞祥, 刘琛, 等. 飞机尾翼前缘结构鸟撞仿真与改进设计[J]. 工程力学, 2022, 39(6): 236 − 246. doi: 10.6052/j.issn.1000-4750.2021.03.0236 SU Kang, BAI Ruixiang, LIU Chen, et al. Bird strike simulation and improved design of leading edge structure of aircraft tail [J]. Engineering Mechanics, 2022, 39(6): 236 − 246. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.03.0236
[25]	WU S T, ZHOU C W, SHI Y H, et al. Plasticity, ductile fracture and ballistic impact behavior of Ti-6Al-4V Alloy [J]. International Journal of Impact Engineering, 2023, 174: 104493. doi: 10.1016/j.ijimpeng.2023.104493
[26]	XUE L, WIERZBICKI T. Ductile fracture initiation and propagation modeling using damage plasticity theory [J]. Engineering Fracture Mechanics, 2008, 75(11): 3276 − 3293. doi: 10.1016/j.engfracmech.2007.08.012
[27]	王俊杰, 王伟. 考虑罗德角参数的钢材薄板延性断裂标定方法[J]. 工程力学, 2019, 36(5): 37 − 43. doi: 10.6052/j.issn.1000-4750.2018.03.0150 WANG Junjie, WANG Wei. Ductile fracture locus validation method of thin steel plates considering the lode angle parameter [J]. Engineering Mechanics, 2019, 36(5): 37 − 43. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.03.0150
[28]	BAI Y L, WIERZBICKI T. Application of extended Mohr–Coulomb criterion to ductile fracture [J]. International Journal of Fracture, 2010, 161(1): 1 − 20. doi: 10.1007/s10704-009-9422-8
[29]	陈爱国, 张佩雲, 蔺军, 等. 基于MMC模型的Q460C高强结构钢延性断裂性能研究[J]. 工程力学, 2024, 41(9): 179 − 190. doi: 10.6052/j.issn.1000-4750.2022.08.0697 CHEN Aiguo, ZHANG Peiyun, LIN Jun, et al. Study on ductile fracture of Q460C high-strength structural steel based on mmc fracture model [J]. Engineering Mechanics, 2024, 41(9): 179 − 190. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.08.0697
[30]	MOHR D, MARCADET S J. Micromechanically-motivated phenomenological Hosford–Coulomb model for predicting ductile fracture initiation at low stress triaxialities [J]. International Journal of Solids and Structures, 2015, 67/68: 40 − 55. doi: 10.1016/j.ijsolstr.2015.02.024
[31]	LOU Y S, YOON J W, HUH H. Modeling of shear ductile fracture considering a changeable cut-off value for stress triaxiality [J]. International Journal of Plasticity, 2014, 54: 56 − 80. doi: 10.1016/j.ijplas.2013.08.006
[32]	XIAO X K, MU Z C, PAN H, et al. Effect of the Lode parameter in predicting shear cracking of 2024-T351 aluminum alloy Taylor rods [J]. International Journal of Impact Engineering, 2018, 120: 185 − 201. doi: 10.1016/j.ijimpeng.2018.06.008
[33]	GORJI M B, MOHR D. Predicting shear fracture of aluminum 6016-T4 during deep drawing: Combining Yld-2000 plasticity with Hosford-Coulomb fracture model [J]. International Journal of Mechanical Sciences, 2018, 137: 105 − 120. doi: 10.1016/j.ijmecsci.2018.01.008
[34]	FRAS T, ROTH C C, MOHR D. Dynamic perforation of ultra-hard high-strength armor steel: Impact experiments and modeling [J]. International Journal of Impact Engineering, 2019, 131: 256 − 271. doi: 10.1016/j.ijimpeng.2019.05.008
[35]	XIAO X K, PAN H, BAI Y L, et al. Application of the modified Mohr–Coulomb fracture criterion in predicting the ballistic resistance of 2024-T351 aluminum alloy plates impacted by blunt projectiles [J]. International Journal of Impact Engineering, 2019, 123: 26 − 37. doi: 10.1016/j.ijimpeng.2018.09.015
[36]	XIAO X K, SHI Y H, WANG Y P, et al. Effect of incorporating lode angle parameter into a fracture criterion in predicting ballistic impact behavior of double-layered 2024-T351 aluminum alloy plates against blunt projectiles [J]. International Journal of Impact Engineering, 2022, 160: 104082. doi: 10.1016/j.ijimpeng.2021.104082
[37]	邓云飞, 张永, 曾宪智, 等. 6061-T651铝合金动态力学性能及断裂准则修正[J]. 机械工程学报, 2020, 56(18): 81 − 91. doi: 10.3901/JME.2020.18.081 DENG Yunfei, ZHANG Yong, ZENG Xianzhi, et al. Dynamic mechanical properties and modification of fracture criteria of 6061-T651 aluminum alloy [J]. Journal of Mechanical Engineering, 2020, 56(18): 81 − 91. (in Chinese) doi: 10.3901/JME.2020.18.081
[38]	LEE J Y, STEGLICH D, LEE M G. Fracture prediction based on a two-surface plasticity law for the anisotropic magnesium alloys AZ31 and ZE10 [J]. International Journal of Plasticity, 2018, 105: 1 − 23. doi: 10.1016/j.ijplas.2017.10.002
[39]	JANG I, BAE G, SONG J, et al. Fracture envelopes on the 3D-DIC and hybrid inverse methods considering loading history [J]. Materials & Design, 2020, 194: 108934.
[40]	LOU Y S, HUH H. Prediction of ductile fracture for advanced high strength steel with a new criterion: Experiments and simulation [J]. Journal of Materials Processing Technology, 2013, 213(8): 1284 − 1302. doi: 10.1016/j.jmatprotec.2013.03.001
[41]	QIAN L Y, FANG G, ZENG P. Modeling of the ductile fracture during the sheet forming of aluminum alloy considering non-associated constitutive characteristic [J]. International Journal of Mechanical Sciences, 2017, 126: 55 − 66. doi: 10.1016/j.ijmecsci.2017.03.013
[42]	FAN F, XU T L, ZHI X D, et al. Research on dynamic constitutive model and fracture criterion of 6082-T6 aluminium alloy [J]. Structures, 2022, 38: 14 − 27. doi: 10.1016/j.istruc.2022.01.071
[43]	梁宾, 赵岩, 赵清江, 等. 基于Gissmo失效模型的6016铝合金板材断裂行为研究及应用[J]. 机械工程学报, 2019, 55(18): 53 − 63. doi: 10.3901/JME.2019.18.053 LIANG Bin, ZHAO Yan, ZHAO Qingjiang, et al. On the prediction of failure in 6016 aluminum alloy sheet by gissmo damage model [J]. Journal of Mechanical Engineering, 2019, 55(18): 53 − 63. (in Chinese) doi: 10.3901/JME.2019.18.053
[44]	DUNAND M, MOHR D. Effect of Lode parameter on plastic flow localization after proportional loading at low stress triaxialities [J]. Journal of the Mechanics and Physics of Solids, 2014, 66: 133 − 153. doi: 10.1016/j.jmps.2014.01.008

施引文献(17)

期刊类型引用(9)

1.	张宏杰，蔡养春，吴军强. 基于NSGA-Ⅱ算法的超声骨刀换能器设计与模态优化. 天津工业大学学报. 2025(02): 84-91 . 百度学术
2.	周宇，陈卫星，赵现朝，高峰. 基于双层可展单元的空间伸展臂设计与分析. 机械设计与研究. 2024(02): 32-39 . 百度学术
3.	欧阳衡，高硕，王世涛，马正琰，张德权. 基于子区间的雷达探测距离和测距精度分析. 工程设计学报. 2024(03): 332-339 . 百度学术
4.	董朋虎，陈强，李彦斌，张旭东，马晗，费庆国. 基于自适应径向基网络的热防护结构可靠性评估. 工程力学. 2024(09): 234-244 . 本站查看
5.	秦礼，房光强，郭俊康，曾令斌. 面向在轨组装的模组天线型面精度建模与调控算法研究. 航天制造技术. 2024(06): 1-9 . 百度学术
6.	张纯，何君儒，周宇轩，林莹. 基于深度神经网络代理模型的盾构隧道密封垫断面优化. 工程力学. 2023(07): 137-144 . 本站查看
7.	张凤玲，张旭，艾延廷，赵亚芝. 基于响应面法的高温应变计敏感栅结构优化研究. 仪器仪表学报. 2023(06): 144-155 . 百度学术
8.	江春，范勤勤，韩新，王维莉，丛北华. 基于多核极限学习机的火灾代理模型研究. 制造业自动化. 2022(12): 39-44 . 百度学术
9.	胡长明，操卫忠，孙为民，芮棽. 基于代理模型的车载雷达阵面风载疲劳分析. 强度与环境. 2020(04): 45-51 . 百度学术