预制拼装式盾构隧道衬砌结构通常在隧道的圆周方向及纵向方向通过螺栓将各个衬砌管片连接起来，形成环向接缝及纵向接缝^[1]。接缝在传递力的同时也削弱了衬砌结构的整体刚度，是整个拼装式结构的薄弱部位。因此，接缝的力学性能，尤其是其抗弯力学性能，严重影响了盾构隧道衬砌结构的力学行为。

为了研究盾构隧道衬砌管片接缝的复杂力学性能及相关力学参数，学者们结合工程实际开展了一系列足尺接头试验，如穿黄隧道^[2-3]、青草沙输水隧道^[4]、广州珠江狮子洋隧道^[5-6]、上海长江隧道^[7]、GIL苏通管廊^[8]、上海市深层排水调蓄隧道^[9]等。这些研究工作取得了丰富的研究成果，为相应工程的顺利建设提供了指导。基于这些足尺试验结果及相应假设，学者们建立了可以较好反映接缝力学特性的理论公式。最典型的是由村上博智和小泉淳^[10]基于卡氏第二定理提出的梁-弹簧模型，但由于假定在接缝处连续变形，该模型无法模拟接缝转动刚度的非线性特征。随后，朱合华等^[11]提出了可以反映接缝刚度非线性特征的梁-弹簧广义模型。张建刚等^[12]基于条带计算思想建立了能够体现管片接缝复杂要素的理论解析算法。耿萍等^[13]建立了可以考虑管片之间剪切作用的力学模型。除此之外，也有学者针对盾构隧道的纵向力学特性开展了一系列研究。志波由纪夫等^[14]基于管片及螺栓的变形与力的平衡关系，推导出了隧道环缝的等效刚度。李晓军等^[15]使用隧道在附加沉降变形条件下的典型内力分布模式来构造内力形函数，建立了基于柔度法的盾构隧道衬砌结构纵向梁模型。鲁选一等^[16]通过管片结构纵向模型试验，研究了盾构隧道的竖向位移及纵向应变，并给出了管片结构纵向刚度有效率与竖向荷载之间的关系。

除足尺试验及理论解析等手段外，对管片进行数值模拟是必要的。这是因为足尺接头试验往往需要耗费巨大的人力、物力，客观条件的限制使得进行大量的各种荷载工况条件的足尺加载试验并不现实^[17]。数值计算方法的可重复性、经济性使得进行各种荷载工况条件下的盾构隧道衬砌管片足尺接头加载试验仿真模拟成为可能。因此，在进行足尺接头试验和理论解析的同时，还常需辅以数值试验来研究不同荷载条件下的接缝力学行为。

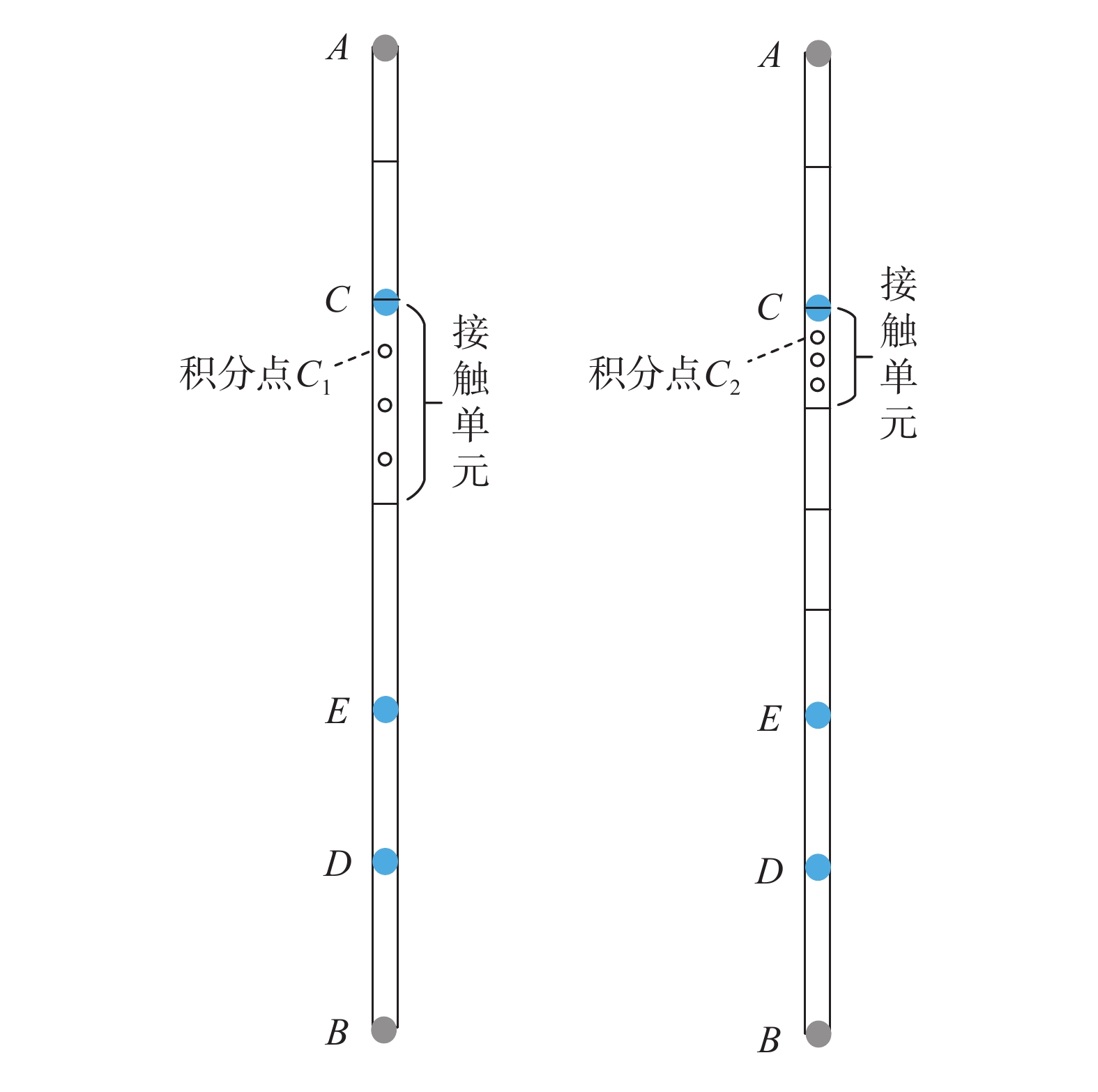
接缝的构造十分复杂，一般由管片、挡水条、密封垫、定位棒、连接螺栓、变形缝等构成，典型的管片接缝细部构造如图1所示。由于嵌缝、密封垫槽、定位孔等的存在以及拼装误差的影响，接缝截面是非连续的，它们将接缝面分为外缘接触面、核心接触面以及内缘接触面。在管片加载过程中，例如正弯矩加载，随着荷载增加，C-D段的核心接触面张开，并逐渐演变为C点接触受压和E点螺栓连接处受拉的受力状态，变形缝所在的外缘接触面不参与承载(继续加载后会变为接触状态直至破坏)。试验和计算分析结果都表明接缝处的接触面长度对管片接缝力学行为有着十分显著的影响，十分有必要对管片接缝面进行合理的模拟。

图  1  管片接缝细部构造

Figure  1.  Structural details of segmental joint

下载: 全尺寸图片 幻灯片

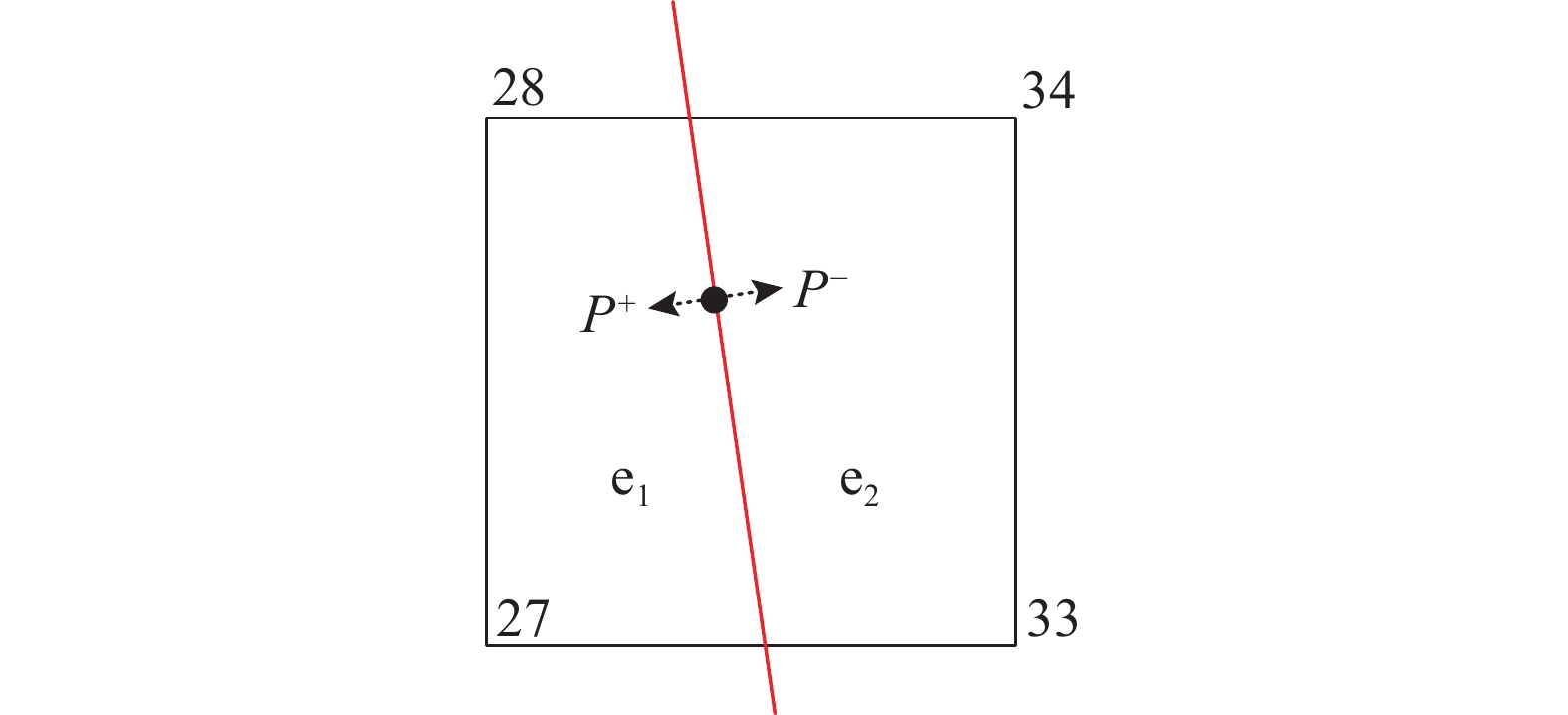
在面-面接触分析中，接触面法向传递接触压力、切向传递剪力。在传统有限元方法里，面-面接触的建立通常有两种方式：约束算法及间隙单元算法。其中，约束算法在法向常采用罚函数法来建立接触体之间的接触行为；间隙单元法在接触面上建立一种体积为0，而材料参数与接触面材料参数相匹配的特殊形式单元，如Goodman单元^[18-19]、虚拟单元^[20]等。相比较于约束算法，间隙单元法学力学意义明确，单元刚度矩阵的计算和组装过程与普通单元类似，使得其在计算机编程时简单高效。在这些间隙单元算法中，接触面的计算依赖于积分点的应力或应变。如图2所示，如果将点C设置为接触单元的边界，当接触单元长度变化时，实际参与计算的积分点C₁和C₂的位置会随着单元长度的变化而变动，这将导致计算结果随着网格尺寸的变动而发生明显变化，表现出十分明显的网格尺寸相关性，较大削弱了数值试验的实用价值。

图  2  接缝处的接触单元示意图

Figure  2.  Diagram of the contact elements at the joint

下载: 全尺寸图片 幻灯片

数值流形方法(Numerical manifold method, NMM)^[21-24]由石根华在1991年提出。在过去的三十年以来，NMM方法得到了快速发展，学者们对NMM方法的位移插值^[25]、覆盖生成算法^[26]、接触算法^[27]等进行了深入的研究。目前，NMM已在裂纹扩展^[28]、隧道开挖与支护^[29]、岩体渐进性破坏^[30]等问题中得到了广泛应用。

为解决传统数值方法中计算结果的网格尺寸相关性，本文利用NMM不需要划分边界相适应计算网格的优点及其十分强大的不连续-连续统一分析能力，建立了用于模拟盾构隧道衬砌管片接缝的NMM数值模型，以及基于虚拟薄层^[31]的、固定积分点的管片接触面接触模型及其生成算法。该盾构隧道衬砌管片接缝模型和接触算法良好克服了传统有限元方法的面-面接触模型在分析该问题时，网格生成受限于模型几何边界和不连续物理边界，以及网格尺寸相关性等问题。与足尺接头试验的对比分析验证了本文方法的正确性和可靠性。

1   衬砌管片接缝的NMM模型

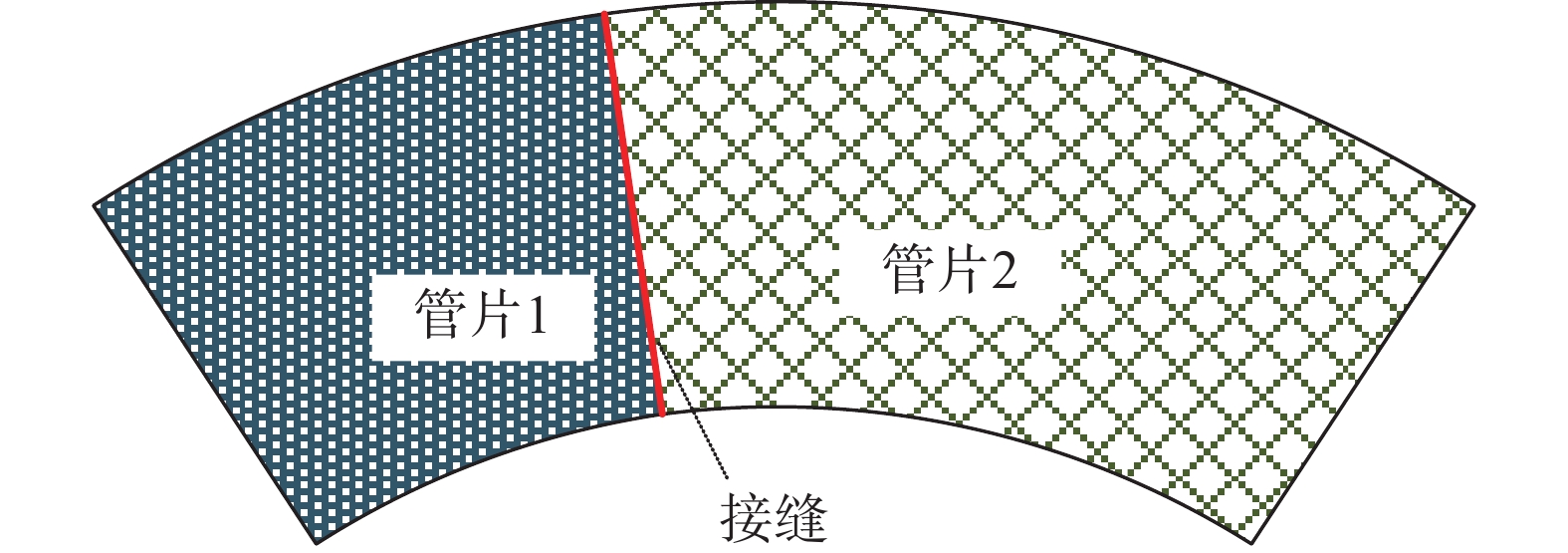
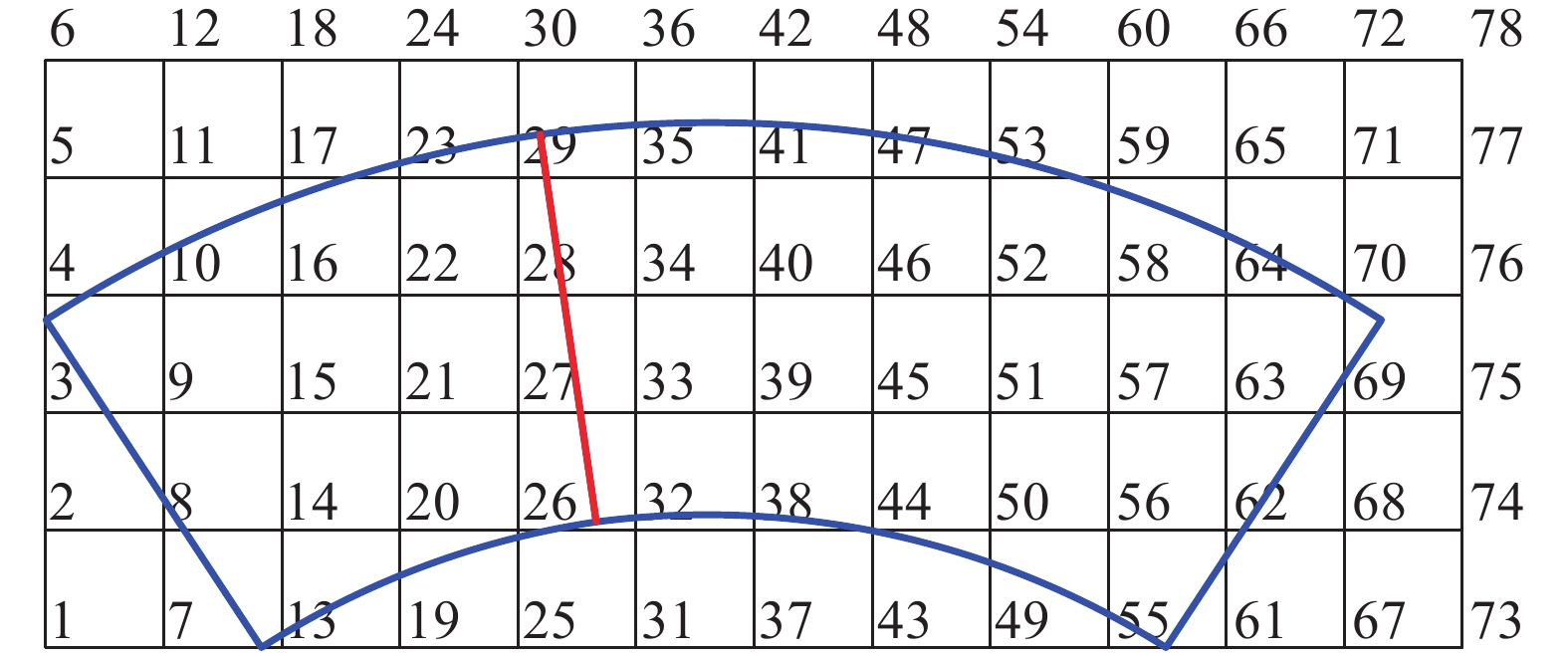
考虑如图3所示的含有接缝的拼装式结构。进行NMM分析时，首先使用一组与几何边界无关的规则正方形网格覆盖整个问题域，如图4所示。称该网格为数学网格，该网格上的结点为数学结点，单元为数学单元。记数学单元的边长为h，并对数学单元、数学结点按照“由左及右、由下往上”的原则进行编号。在图4中，共有78个数学结点、60个数学单元。

图  3  拼装式结构模型

Figure  3.  Assembled structure model

下载: 全尺寸图片 幻灯片

图  4  覆盖定义域的数学网格

Figure  4.  Mathematical mesh to cover problem domain

下载: 全尺寸图片 幻灯片

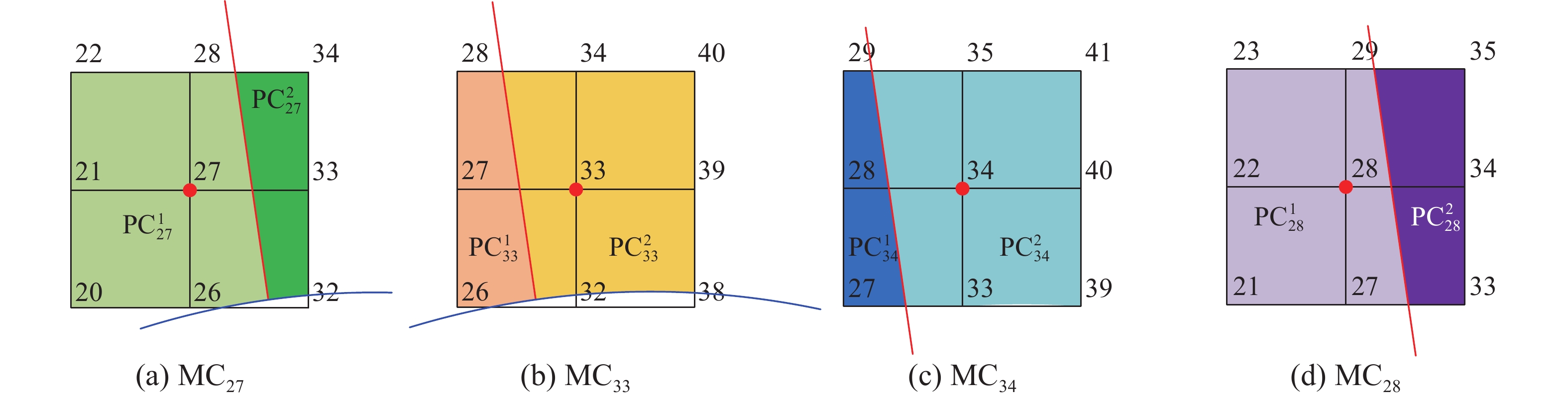
定义以结点i为顶点的所有数学单元所组成的区域为数学覆盖(或数学片^[32])，记为MC_i (i = 1 ~ n)，其中n为结点个数，也即是数学覆盖个数。如图5所示，数学覆盖MC₂₇为结点26-32-33-34-28-22-21-20所围成的封闭区域，数学覆盖MC₃₃为结点32-38-39-40-34-28-27-26所围成的封闭区域，数学覆盖MC₃₄为结点33-39-40-41-35-29-28-27所围成的封闭区域，数学覆盖MC₂₈为结点27-33-34- 35-29-23-22-21所围成的封闭区域。

图  5  数学覆盖被剖分为多边形物理覆盖

Figure  5.  Divide mathematical cover into polygon physical covers

下载: 全尺寸图片 幻灯片

数学覆盖MC_i进一步被不连续线、边界线等物理线剖分成多个不连续区域，称这些区域为物理覆盖(或物理片^[32])，记为${\rm{PC}}_i^I\left( {I = 1\sim N} \right)$，其中I为数学覆盖MC_i被物理线剖分形成的子域数(即物理覆盖的个数)。从集合的角度来看，物理覆盖是数学覆盖与物理域的交集。在图5中，数学覆盖MC₂₇被接缝线及边界线切割形成物理覆盖${\rm{PC}}_{27}^1$及${\rm{PC}}_{27}^2$，同样，数学覆盖MC₃₃形成物理覆盖${\rm{PC}}_{33}^1$及${\rm{PC}}_{33}^2$，数学覆盖MC₃₄形成物理覆盖${\rm{PC}}_{34}^1$及${\rm{PC}}_{34}^2$， 数学覆盖MC₂₈形成物理覆盖${\rm{PC}}_{28}^1$及${\rm{PC}}_{28}^2$。

按照NMM理论，不同的物理覆盖在同一数学单元上的交集形成计算所需的流形单元。如图6所示，在数学单元27-33-34-28上，流形单元e₁为物理覆盖${\rm{PC}}_{27}^1$、${\rm{PC}}_{33}^1$、${\rm{PC}}_{34}^1$、${\rm{PC}}_{28}^1$的交集，流形单元e₂为物理覆盖${\rm{PC}}_{27}^2$、${\rm{PC}}_{33}^2$、${\rm{PC}}_{34}^2$、${\rm{PC}}_{28}^2$的交集。

图  6  数学单元27-33-34-28上的流形单元

Figure  6.  Manifold elements in the element 27-33-34-28

下载: 全尺寸图片 幻灯片

有了上述基本定义后，流形单元内任意点x的全局位移近似函数即可按单位分解方法表达为：

式中：${\omega _i}$为定义在数学覆盖MC_i上的权函数，直接取为对应有限元法中四边形单元的形函数，它恰好能够满足NMM对权函数的要求^[22]；${\boldsymbol{u}}_i^I\left( {\boldsymbol{x}} \right)$为定义在物理覆盖${\rm{PC}}_i^I$上的局部覆盖函数，可以采用简单多项式或各种级数形式的分片插值函数。当采用常量形式的局部覆盖函数时，式(1)可以进一步地被表示为：

式中：${\boldsymbol{\varPhi }}$为形函数矩阵；${\boldsymbol{a}}$为待求解自由度列向量。

式中，下标1~4为与该流形单元相关的4个物理覆盖的局部编号。

如图6所示，不连续线两侧的点${P^ + }$、${P^ - }$分别位于流形单元e₁、e₂中。虽然两个流形单元的权函数相同，但由于它们属于不同的物理覆盖，其局部覆盖函数是独立存在的，自然地，两者的位移插值是不同的，从而实现了对不连续线的自然模拟。

有了任意点的位移插值函数之后，可以根据最小势能原理^[21]或虚功原理^[22]得到流形单元e的刚度矩阵${{\boldsymbol{K}}^{\left( {\rm{e}} \right)}}$及荷载列阵${{\boldsymbol{P}}^{\left( {\rm{e}} \right)}}$为：

式中：D为材料矩阵；${\boldsymbol{B}} = {\boldsymbol{L\varPhi }}$为应变矩阵；L为微分算子矩阵；${{\boldsymbol{F}}^{\rm{e}}}$、f、b分别为作用在流形单元e上的集中荷载、面荷载、体荷载。

然后像有限元法一样，按照自由度将其组集到整体刚度矩阵K及整体荷载列阵P中，并使用罚函数法、拉格朗日乘子法、间断伽辽金方法等来施加位移边界条件^[22]，本文采用虚拟薄层^[31]来施加，随后即可得到全域上的离散控制方程为：

其中：

2   基于虚拟薄层单元的接触模型

2.1   虚拟薄层单元

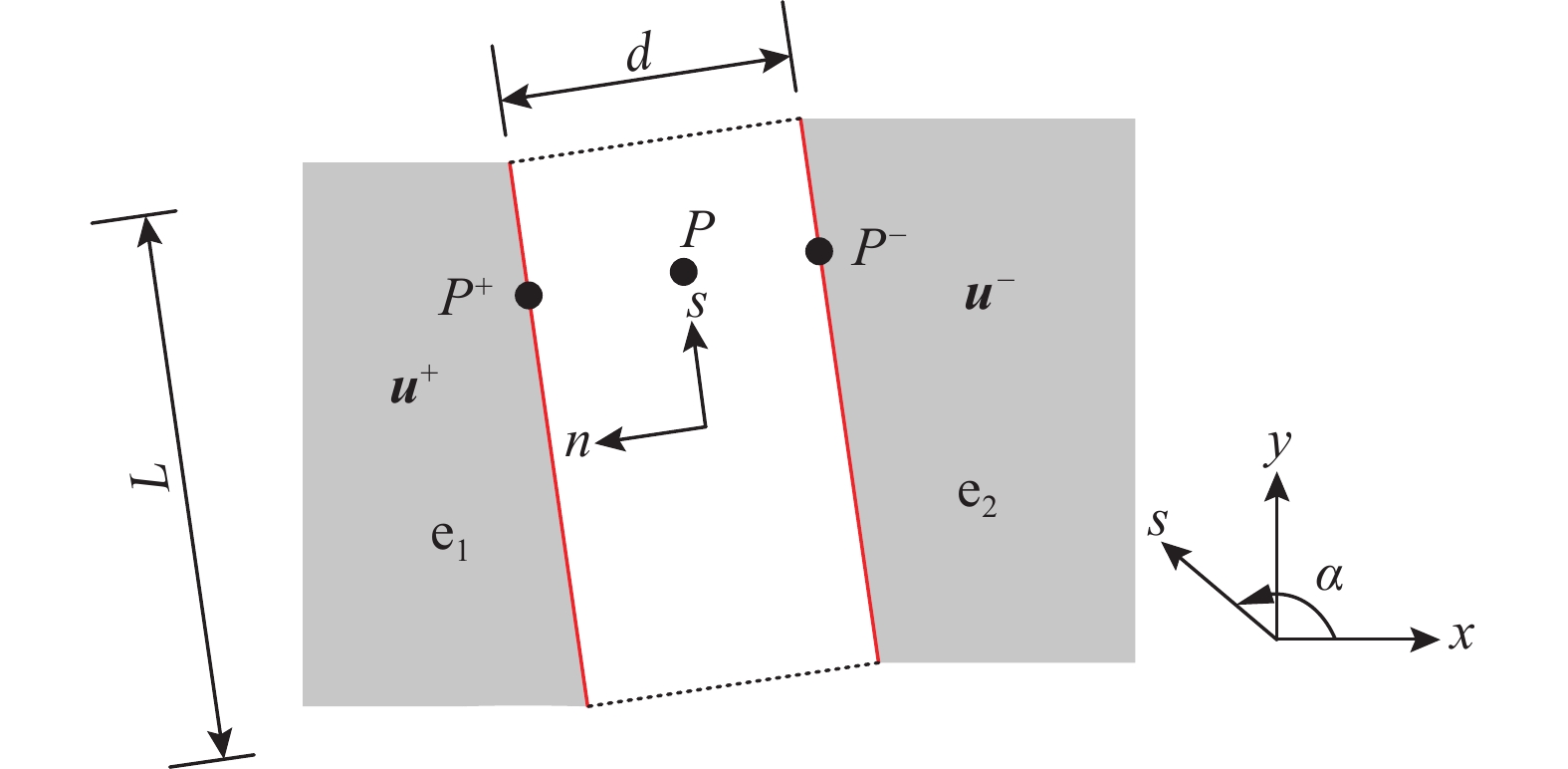
假设图6中接缝不连续线两侧的两个流形单元之间存在一厚度为d、长度为L的薄层单元，如图7所示，其中，$d \ll L$。

图  7  沿着不连续线的虚拟薄层单元

Figure  7.  Virtual thin layer along discontinuity line

下载: 全尺寸图片 幻灯片

图7中虚拟薄层单元内点P在局部坐标系(s, n)下的位移${\overline {\boldsymbol{u}}^{\rm{L}}}$为：

式中，${\overline {\boldsymbol{u}}^ + } = {[ {{{\overline u}^ + }}\;\;\;{{{\overline v}^ + }} ]^{\text{T}}}$、${\overline {\boldsymbol{u}}^ - } = {[ {{{\overline u}^ - }}\;\;\;{{{\overline v}^ - }} ]^{\text{T}}}$分别为P的邻近点${P^ + }$、${P^ - }$在局部坐标系下的位移，由整体坐标系下的位移${{\boldsymbol{u}}^ + } = {[ {{u^ + }}\;\;\;{{v^ + }} ]^{\text{T}}}$、${{\boldsymbol{u}}^ - } = {[ {{u^ - }}\;\;\;{{v^ - }} ]^{\text{T}}}$经坐标转换得到，即：

式中，${\boldsymbol{\lambda }}$为整体坐标到局部坐标的转换矩阵：

将式(2)代入式(11)，再代入式(10)可得：

式中：${{\boldsymbol{\varPhi }}^ + }$、${{\boldsymbol{\varPhi }}^ - }$分别为接缝两侧流形单元的形函数矩阵；${{\boldsymbol{a}}^ + }$、${{\boldsymbol{a}}^ - }$为相应的自由度向量。式(13)可进一步简写为：

式中：${{\boldsymbol{\varPhi }}^{\rm{L}}} = {\boldsymbol{\lambda }}[ {{{\boldsymbol{\varPhi }}^ + }}\;\;\;{ - {{\boldsymbol{\varPhi }}^ - }} ]$；${{\boldsymbol{a}}^{\rm{L}}} = {[ {{{\boldsymbol{a}}^{\text{ + }}}}\;\;\;{{{\boldsymbol{a}}^ - }} ]^{\text{T}}}$。

由于$d \ll L$，参考Goodman单元假设^[18]，虚拟薄层内点P的应变可以近似为：

将式(14)代入式(15)并简写为：

对于弹性分析，根据胡克定律，可以得到虚拟薄层单元内P点的应力为：

其中：

式中：${G_0} = E/\left( {2\left( {1 + \nu} \right)} \right)$、${E_0} = E/\left( {1 - {\nu^2}} \right)$，E、ν分别为接缝两端混凝土实体的弹性模量、泊松比；d为虚拟薄层单元厚度，文献[31]中的数值算例表明虚拟薄层厚度对计算结果的精度影响很小，本文取为${10^{ - 4}}h$。

根据最小势能原理或虚功原理可进一步推出该虚拟薄层单元的单元刚度矩阵为：

然后，将虚拟薄层单元的单元刚度矩阵${{\boldsymbol{K}}^{\rm{L}}}$按照自由度${{\boldsymbol{a}}^{\rm{L}}}$组集到整体刚度矩阵K(式(8))中。

2.2   接触模型非线性迭代算法

在加载过程中，管片之间原来接触的部分逐渐脱开，管片的受力行为呈现出强烈的非线性，因此在加载过程中采用增量加载。在每个增量步开始前，首先根据式(18)计算接缝面上各个虚拟薄层单元的积分点材料矩阵${\overline {\boldsymbol{D}}^{\rm{L}}}$；然后检查各积分点的接触状态，当接缝面在某点法向受拉时，表明接触面在该点脱开，即定义接触判定准则为：

式中，${S_{\rm{t}}}$为接触面的抗拉强度，一般取为0，为了数值实施方便，本文取为10⁻¹⁰。当接缝处虚拟薄层单元上的积分点法向应力满足式(20)时，更新式(18)中的材料矩阵为：

同时，将该点的各向应力调整为：

然后，检查平衡方程的残余力是否收敛，若不收敛则继续求解平衡方程，并执行上述过程直至平衡方程残余力收敛。某个增量步中具体的迭代过程如图8所示。

图  8  接触面迭代算法流程图

Figure  8.  Iterative algorithm for contact surface

下载: 全尺寸图片 幻灯片

2.3   固定积分点位置的虚拟薄层单元生成算法

一般的虚拟薄层单元生成算法包含三个步骤，即：首先根据外缘、内缘接触面的长度确定实际有效接触面两端的端点，然后以实体数学单元边长h为步长对实际有效接触面进行剖分，最后根据剖分线段形成虚拟薄层单元。由第2.2节可知，接触面的计算依赖于积分点。在生成虚拟薄层单元时，如果不做特殊处理，积分点的位置会随网格单元长度变化而变动，这将使计算结果表现出十分明显的网格尺寸相关性，削弱数值试验的实用价值。因此，需要在接缝面的实际有效接触面两端各设置一个积分点，以保证接触面的实际有效接触长度不受网格尺寸的影响。

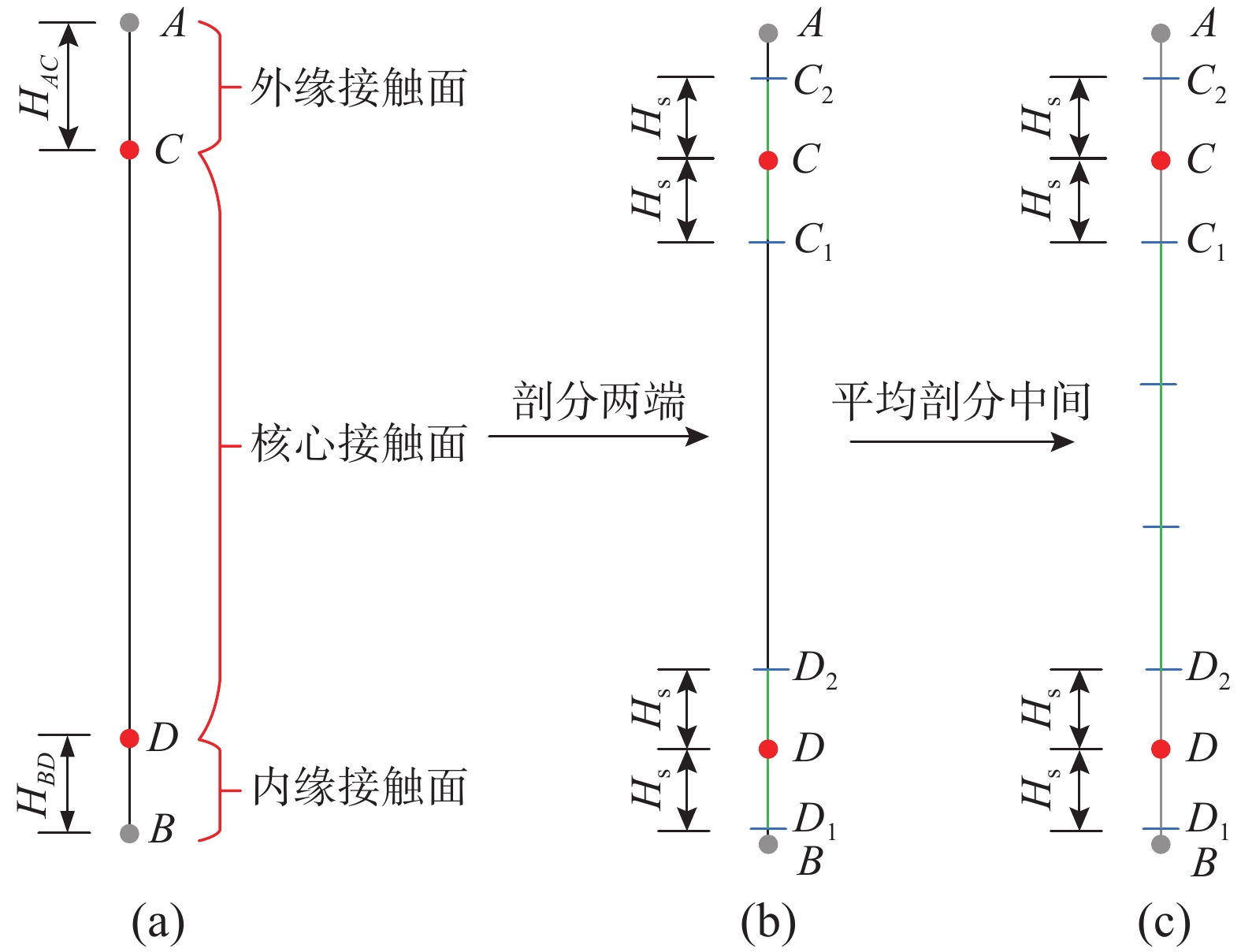
有一接缝A-B，如图9(a)所示，接缝两端点A、B的坐标分别为$\left( {{x_A},{y_A}} \right)$、$\left( {{x_B},{y_B}} \right)$。根据图1，接缝的实际有效接触为核心接触面C-D，外缘接触面A-C及内缘接触面B-D不接触。记外缘接触面A-C的长度为H_AC、内缘接触面B-D的长度为H_BD。在该接缝面上生成虚拟薄层单元时，需要保证在C、D两点处各存在一个有效积分点，相关算法如下：

图  9  虚拟薄层单元生成方法

Figure  9.  Generation method for virtual thin layer element

下载: 全尺寸图片 幻灯片

1)确定实际有效接触面两端点C、D的坐标为：

式中，$\left( {{n_1},{n_2}} \right)$为直线A-B的方向向量。

2)如图9(b)所示，分别以C、D为中心点，以H_s为步长，在A-B线上确定C、D点的两边点C₁、C₂以及D₁、D₂点的坐标为：

式中，${H_{\rm{s}}} = 0.5 \times \min \left( {{H_{AC}},{H_{BD}},h} \right)$。

3)以2H_s为步长剖分接触面剩余的部分C₁-D₂，如图9(c)所示。

4)根据每一个剖分段生成相应的虚拟薄层单元，当高斯点个数为奇数时，则中间接触面两端一定存在一个积分点。

5)最后，将不接触面范围(A-C、B-D)内的积分点删除，即在计算虚拟薄层单元刚度矩阵时，处于外缘接触面以及内缘接触面范围的积分点对整体刚度矩阵的贡献忽略不计。

上述虚拟薄层单元的生成算法可以保证在核心接触面的两端点各有一个积分点，即确保了在计算过程中接缝的实际有效接触面长度不随网格尺寸的变化而变化。该思路也适用于其他数值方法中的接触分析。

3   试验验证及讨论

3.1   管片接头足尺试验

上海市某地铁隧道管片采用单层衬砌，衬砌管片外径6.2 m、内径5.5 m、幅宽1.2 m。管片混凝土强度等级C55，环向接缝采用2根M30直螺栓进行连接，螺栓长度为472 mm，强度等级为5.8级。材料参数如表1所示。

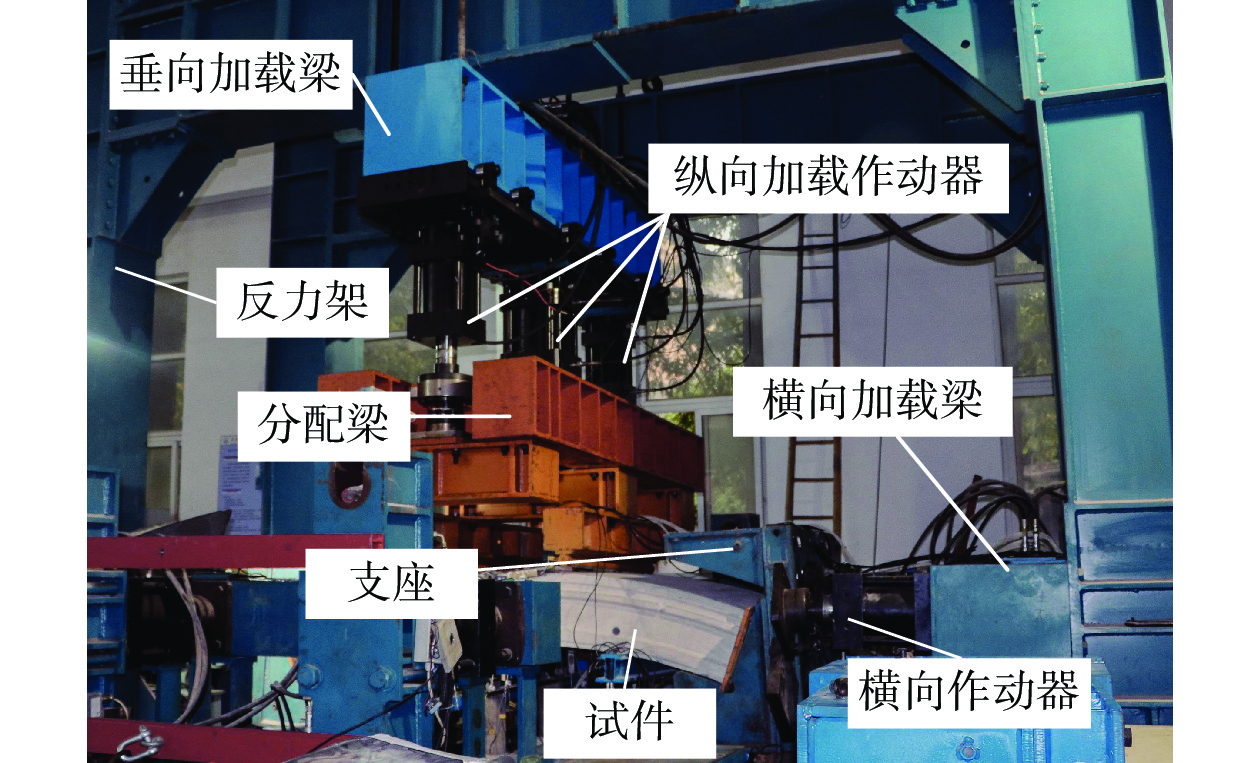
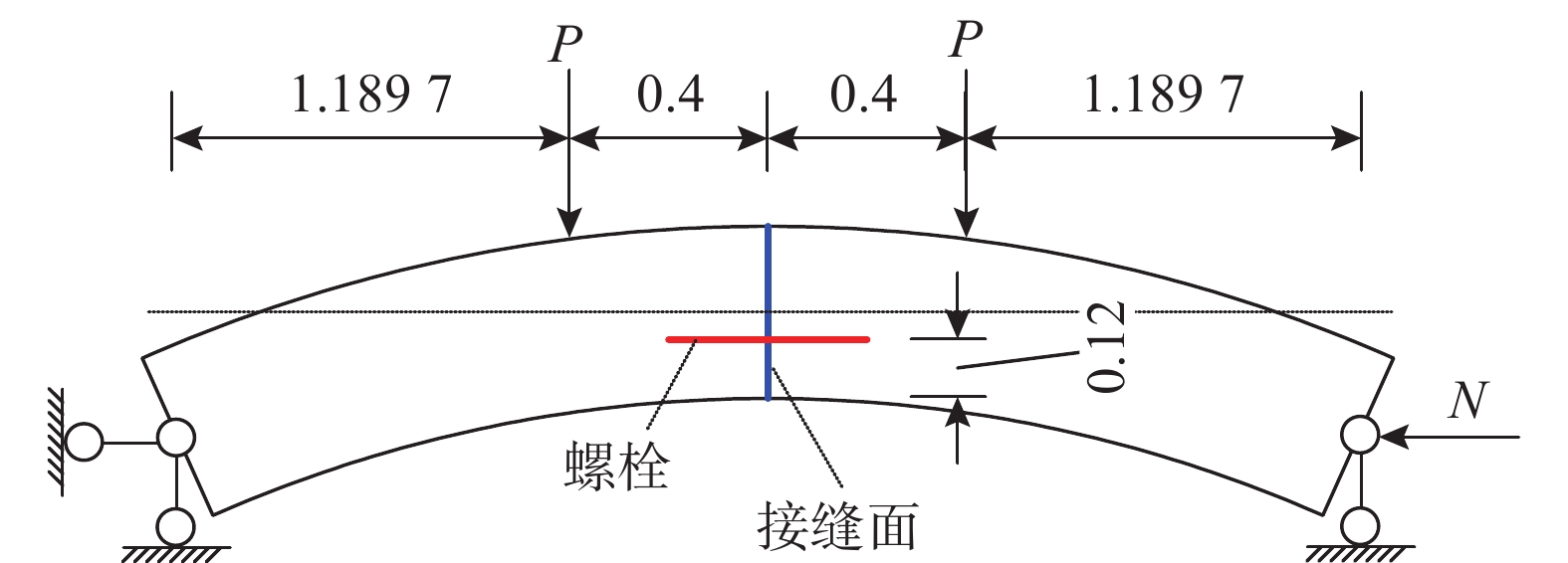
表  1  管片材料参数

Table  1.  Mechanical parameters for lining structure

材料参数	混凝土管片	螺栓
弹性模量E/GPa	35.5	206.0
泊松比ν	0.2	0.3
重度r/(kN/m3)	25.0	78.4

下载: 导出CSV 

| 显示表格

文献[33-34]对原型管片进行加载试验并进行了数值研究。加载系统由自平衡反力架、竖向及横向作动器、支座等组成，如图10所示。其中，横向作动器提供水平荷载用以模拟接头轴力，竖向作动器提供竖向荷载用以导入接头弯矩。试件宽度保持幅宽1.2 m，其他几何参数及等效加载示意图如图11所示。采用等轴力的加载方式，具体分为两步：1)先施加水平轴力N至预定值，并同步施加相应的竖向荷载至P₁以消除初始偏心距产生的负弯矩；2)然后保持水平轴力N不变，不断增加竖向荷载至P₂。

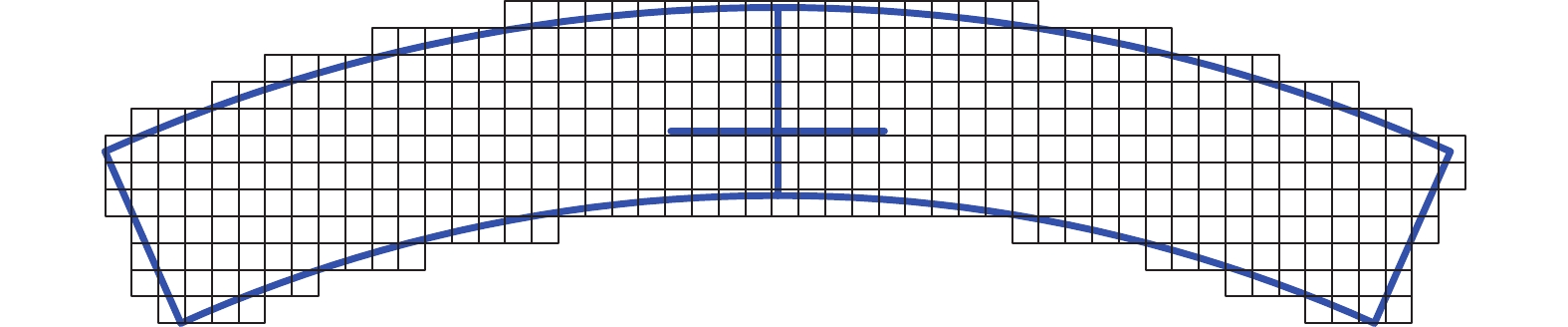
在建立管片接头试验的NMM数值分析模型时，螺栓采用点锚式，实际有效受力长度为400 mm，单位管片宽度方向的螺栓面积为1178.1 mm²，采用双折线模型，屈服强度取为400 MPa，屈服阶段的弹性模量取为弹性阶段的0.2倍。试件外缘接触面长度H_AC = 0.071 m、内缘接触面长度H_BD = 0.06 m。水平轴力N = 750 kN/m(对应于试验工况N = 900 kN)、竖向荷载P₁ = 250 kN/m、P₂ = 521 kN/m。数学单元长度h分别取为0.1 m、0.05 m、0.025 m，图12给出了数学单元长度h = 0.05 m的NMM数学网格配置。

图  10  管片接头足尺试验加载系统

Figure  10.  Loading system for full-scale joint test

下载: 全尺寸图片 幻灯片

图  11  管片接头足尺试验等效加载示意图　/m

Figure  11.  Equivalent loading scheme for full-scale joint test

下载: 全尺寸图片 幻灯片

图  12  管片接头NMM数学网格布置(h = 0.05 m)

Figure  12.  Configuration of mathematical mesh of the NMM model (h = 0.05 m)

下载: 全尺寸图片 幻灯片

作为对比，本文同时使用有限元方法(FEM)对该问题进行了分析。在ABAQUS中建立FEM模型时，几何参数、材料参数、荷载参数等参数与上述NMM模型一致。另外，在该问题的FEM模型中，需要定义螺栓与管片、管片与管片之间的接触关系。在本工作中，螺栓的两端通过“Tie”与混凝土管片连接。管片与管片之间通过“Surface-to-Surface”建立接触关系，其中法向接触设为“硬接触”，切向界面接触力大小与摩擦系数成正比，摩擦系数取为0.4。混凝土管片采用四结点双线性平面应力单元(CPS4)，螺栓采用两结点线性杆单元(T2D2)，采用自由网格划分技术对该问题进行离散，图13给出了当网格单元长度取为0.05 m时该问题的FEM离散模型。

图  13  管片接头FEM离散模型(h = 0.05 m)

Figure  13.  Configuration of finite element mesh (h = 0.05 m)

下载: 全尺寸图片 幻灯片

对比图12及图13可以看到，NMM中的数学网格不需要与几何边界相适应。NMM的这种网格不相关性较大地减轻了生成满足分析需要的高质量网格的负担，有效简化了复杂不连续问题的前处理过程。

分别使用上述NMM模型以及FEM模型对该问题进行分析，从计算结果中提取接缝张开随弯矩的变化情况，并与足尺试验结果进行对比，将对比结果绘于图14。由图14(a)可知，采用本文方法得到的计算结果与试验结果吻合较好。由图14(b)可知，FEM计算结果会随着网格尺寸的变化而变化，表现出较强的网格相关性。进一步对比图14(a)及图14(b)可以看出，本文方法不受网格尺寸的影响，其计算结果更稳定，可以良好克服传统方法所存在的计算结果与网格相关的缺点，方便衬砌管片力学行为的进一步研究。

图  14  管片接缝内侧张开位移随弯矩的变化情况

Figure  14.  Variation of joint opening with bending moment

下载: 全尺寸图片 幻灯片

3.2   外缘接触面长度对接缝抗弯性能的影响

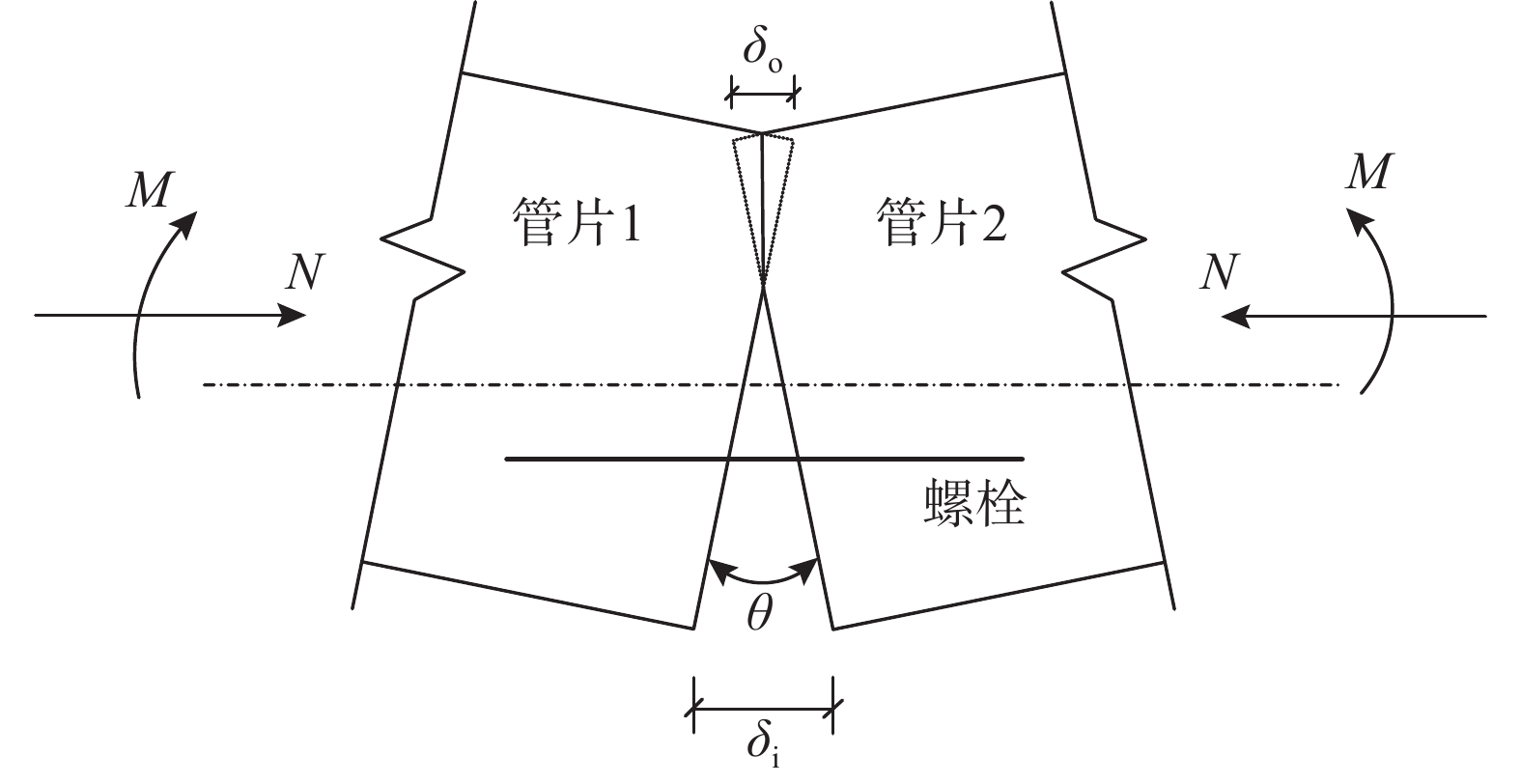
对于第3.1节中的弧形管片接头正弯矩试验来说，接缝位置的外缘接触面长度严重影响着管片接缝的力学行为。本节采用第2节中的接触模型以及第3.1节的NMM数值模型考察不同外缘接触面长度时管片接缝的力学响应及其对接缝刚度的影响。数学单元长度h取为0.025 m，保持内缘接触面长度H_BD为0.06 m，考察外缘接触面长度H_AC取为0.00 m、0.02 m、0.04 m、0.06 m、0.08 m、0.10 m、0.12 m时管片接头的力学响应。接缝转角θ如图15所示，定义为：

式中：${\delta }_{\rm{i}}$为内侧张开位移；${\delta }_{\rm{o}}$为外侧压缩位移；H为管片厚度。接缝转动刚度${K_\theta }$定义为接缝产生单位转角所需要的弯矩，一般通过割线法或切线法求得，本文采用割线法，即：

式中：$\Delta M$为每个荷载增量步中的弯矩增量；$\Delta \theta$为每个荷载增量步中的接缝转角增量。

图  15  接缝转角示意图

Figure  15.  Schematic diagram of joint rotation angle

下载: 全尺寸图片 幻灯片

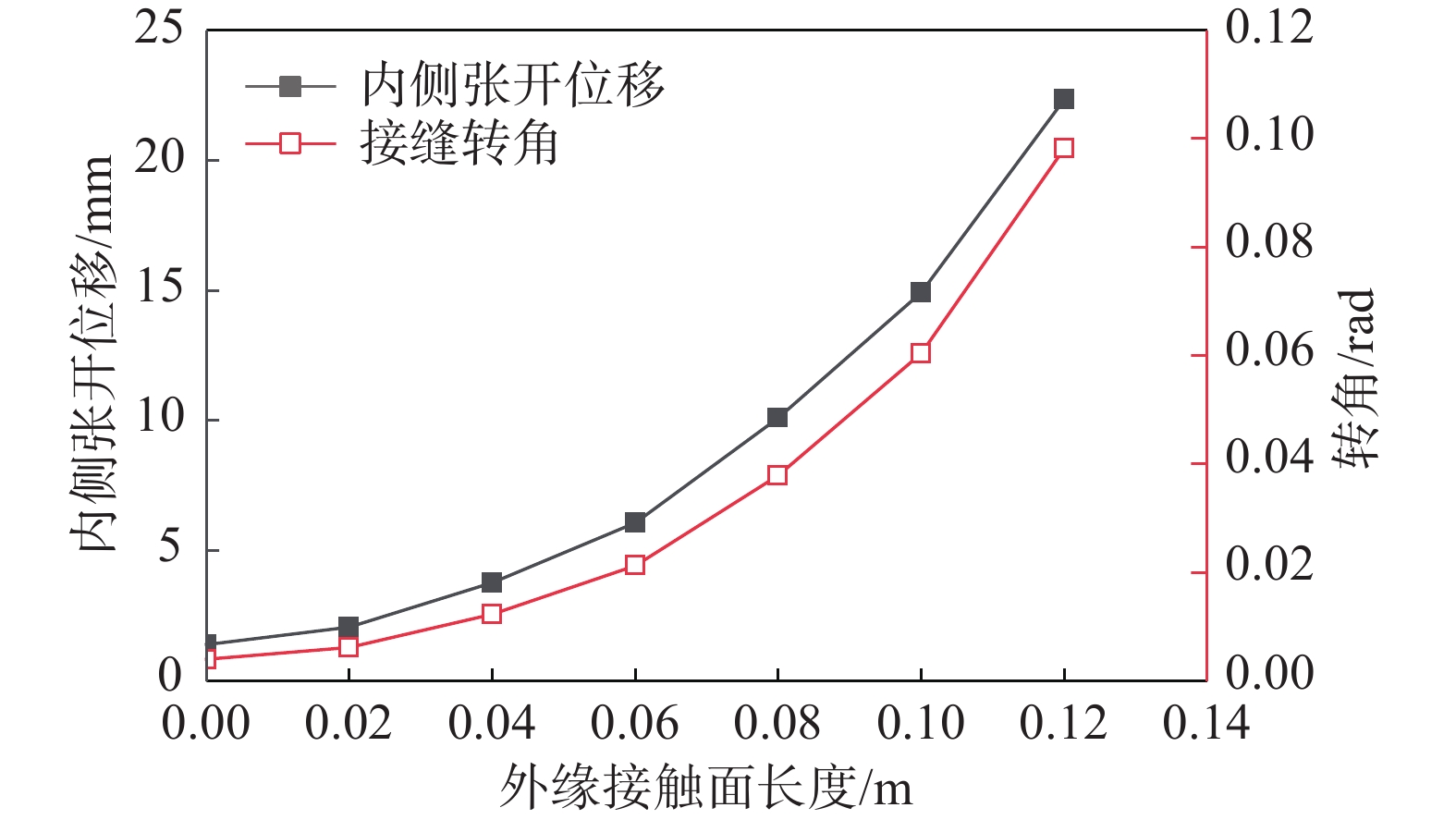
图16给出了不同外缘接触面长度时接缝张开位移以及转角随弯矩的变化情况。可以看出，在第3.1节的荷载作用下，外缘接触面长度为0时(实际接触长度0.29 m)，内侧张开位移仅为1.41 mm，接缝转角仅为0.004 rad。随着外缘接触面长度增加，即实际有效接触长度的减少，接缝内侧张开位移以及接缝转角都显著增大，试件越来越柔，当外缘接触面长度增加至0.12 m时(实际接触长度0.17 m)，内侧张开位移、接缝转角分别急剧增加至22.3 mm、0.098 rad，比外缘接触面长度为0时大15倍、23.5倍。图17进一步给出了接缝内侧张开位移以及接缝转角随外缘接触面长度的变化情况，可以看出，内侧张开位移及接缝转角随着实际接触面的减小近似呈指数级增加。

图  16  管片接缝力学响应对比

Figure  16.  Mechanical responses of segmental joint

下载: 全尺寸图片 幻灯片

图  17  内侧张开位移及转角随外缘接触面长度的变化情况

Figure  17.  Variation of joint opening and rotation angle with different lengths of outer contact surface

下载: 全尺寸图片 幻灯片

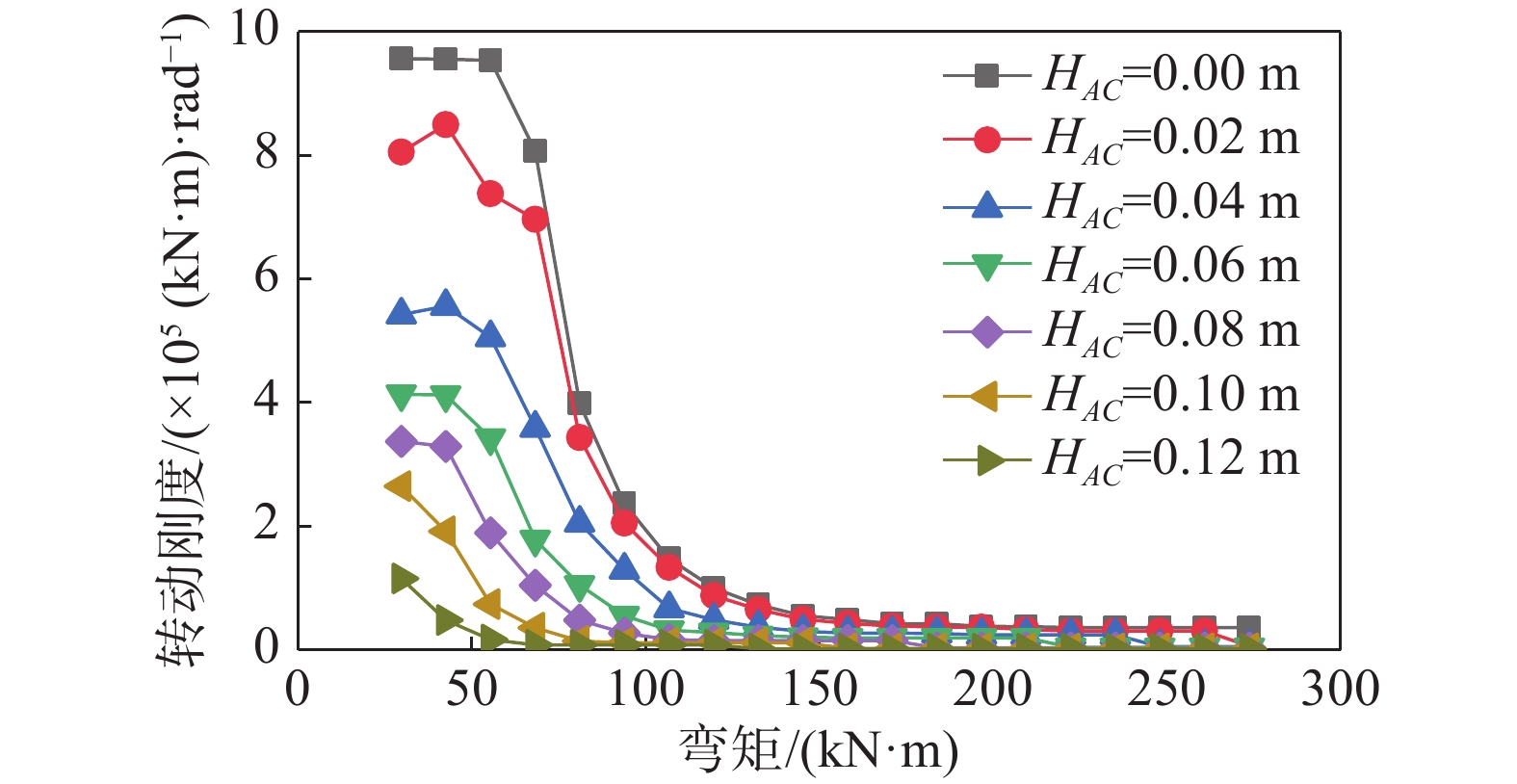
根据式(26)计算各种工况下的接缝转动刚度，将转动刚度随弯矩的变化情况绘制于图18中。可以看到，随着外缘接触面长度的增大，即实际接触面长度的减小，接缝转动刚度显著下降。需要指出的是，在加载初期，计算得到的接缝转动刚度值并不稳定，这是由于初始偏心距的存在使得在加载步1)中接缝张开过小甚至表现为压缩，这时采用基于割线法的式(26)计算得到的接缝转动刚度值有所跳动。

进一步观察图16(b)中的弯矩-转角曲线可以看出，随着外缘接触面长度不断增加，接缝转动刚度的三线性模型特征也越来越明显，通过线性拟合可以得到各阶段的接缝转动刚度，并将其列于表2。可以看出，随着外缘接触面长度的增大，各阶段的接缝转动刚度均大幅度减小，相比于外缘接触面长度0.02 m (实际有效接触面长度0.27 m)，当外缘接触面长度增加至0.12 m (实际有效接触面长度减小至0.17 m)时，三阶段的转动刚度值分别减小94%、79%、73%。

图  18  接缝转动刚度随弯矩变化情况

Figure  18.  Variation of rotational stiffness with bending moment

下载: 全尺寸图片 幻灯片

表  2  接缝转动刚度三阶段模型的拟合刚度值

Table  2.  Fitted values of rotational stiffness for trilinear model

外缘接触面长度HAC/m	转动刚度/(kN·m/rad)
	Kθ1	Kθ2	Kθ3
0.00	685 019	44 600	−
0.02	412 625	38 459	6350
0.04	251 291	28 294	5179
0.06	120 212	21 125	4145
0.08	95 030	16 072	3232
0.10	58 581	11 747	2428
0.12	22 788	8209	1737

下载: 导出CSV 

| 显示表格

由上述分析可知，接缝处的实际有效接触长度严重影响着管片接缝的力学行为及其转动刚度，随着实际接触面的减小，内侧张开位移及接缝转角呈指数级增加，接缝转动刚度值也大幅减小。因此，在盾构隧道施工过程中要注意管片拼装精度，保证管片之间充分接触。

4   结论

本文建立了盾构隧道衬砌管片接缝的NMM数值模型，并基于虚拟薄层发展了用于固定积分点位置的接缝接触模型及相应的非线性迭代算法。与接头足尺试验的对比分析表明了本文方法的有效性及正确性。使用所建立的管片接缝ΝΜΜ数值模型进一步考察了不同外缘接触面长度时的管片接缝力学行为，分析了管片间实际接触长度对接缝变形及转动刚度的影响。主要有以下结论和创新点：

(1)基于数学覆盖及物理覆盖的NMM，不要求几何物理线与数学网格相适应，较大减轻了生成满足分析需要的高质量网格的负担，可以实现对管片接头在接缝处不连续的自然模拟。

(2)在NMM理论框架内，基于虚拟薄层单元建立的、固定积分点的接缝接触模型，其计算精度不受网格单元长度的影响，保证了计算结果的稳定性，可以良好克服传统方法计算结果与网格相关的缺点。

(3)使用本文方法对管片接缝的计算结果表明，接缝处的实际有效接触长度显著影响着管片接缝的力学行为及其转动刚度。因此，在盾构隧道设计与施工过程中要注意管片间的接触长度及其拼装精度，并分析验算实际接缝刚度。