近断层地震动作用下浅埋综合管廊地震易损性研究

张海; 王程西; 王岱; 刘中宪; 孟思博

doi:10.6052/j.issn.1000-4750.2023.02.0071

近断层地震动作用下浅埋综合管廊地震易损性研究

张海^{1, 2,},
王程西^2,,
王岱^{1, 2, ,},
刘中宪^{1, 2,},
孟思博^{1, 2,}

1.
天津市土木建筑结构防护与加固重点实验室，天津 300384
2.
天津城建大学土木工程学院基础设施防护和环境绿色生物技术国际联合研究中心，天津 300384

基金项目: 国家自然科学基金项目(51878434，51908401)；天津市科技计划项目(22KPXMRC00150)

详细信息

作者简介:
张　海(1977−)，男，河北人，教授，博士，博导，主要从事工程结构防灾研究(Email: zhanghai@tcu.edu.cn)

王程西(1996−)，男，河南人，硕士生，主要从事结构抗震研究(Email: wangchengxi978@163.com)

刘中宪(1982−)，男，河南人，教授，博士，博导，主要从事地震工程研究(Email: zhongxian1212@163.com)

孟思博(1990−)，女，黑龙江人，讲师，博士，主要从事结构抗震研究(Email: sibomeng@yeah.net)

通讯作者:
王　岱(1981−)，男，山西人，讲师，博士，主要从事结构抗震研究(Email: wgd@tcu.edu.cn)

中图分类号: TU990.3；TU311.3
计量
- 文章访问数: 217
- HTML全文浏览量: 31
- PDF下载量: 57
出版历程
- 收稿日期: 2023-01-31
- 修回日期: 2023-05-25
- 网络出版日期: 2023-06-08
- 刊出日期: 2024-01-31

STUDY ON SEISMIC FRAGILITY OF SHALLOW BURIED UTILITY TUNNEL UNDER NEAR-FAULT GROUND MOTION

ZHANG Hai^{1, 2,},
WANG Cheng-xi^2,,
WANG Dai^{1, 2, ,},
LIU Zhong-xian^{1, 2,},
MENG Si-bo^{1, 2,}

1.
Tianjin Key Laboratory of Civil Structure Protection and Reinforcement, Tianjin 300384, China
2.
School of Civil Engineering, Joint Research Centre for Protective Infrastructure Technology and Environmental Green Bioprocess, Tianjin Chengjian University, Tianjin 300384, China

摘要

摘要:
为准确评估近断层地震动作用下浅埋综合管廊的地震损伤，利用ABAQUS建立土-结构整体有限元模型，以综合管廊层间位移角最大值为损伤指标，基于IDA方法进行结构地震易损性分析，重点考察近断层地震动强度指标和场地土特性对综合管廊抗震性能的影响。结果表明：近断层地震动加速度型指标的离散性最小，建议选取加速度型指标PGA、Sa作为地震动强度指标；以有限元计算数据为样本，采用BP神经网络可高效预测综合管廊结构的地震损伤，PGA、Sa及土体剪切模量对综合管廊地震易损性分析的影响较大，随着土体剪切模量的增大，超越概率逐渐减小，同时，LS、CP状态的超越概率变化范围要明显大于OP、IO状态；考虑PGA和Sa双参数更能准确反映不同地震动参数对结构损伤的影响，而仅考虑PGA或Sa单参数有可能高估结构的损伤程度。因此，对综合管廊等浅埋地下结构进行地震易损性分析时，建议综合考虑PGA和Sa的影响。
- 综合管廊 /
- 近断层地震动 /
- 地震易损性 /
- 强度指标 /
- BP神经网络
Abstract:
In order to accurately evaluate the seismic damage of shallow buried utility tunnel under near-fault ground motion, ABAQUS is used to establish the finite element model of whole soil-structure, while the analysis of seismic fragility of structure is conducted based on the incremental dynamic analysis (IDA) method with the maximum of inter-story displacement angle of utility tunnel as the damage measure, and the influence of both the intensity measure of near-fault ground motion and the characteristics of site soil on the seismic performance of utility tunnel is investigated. The results show that the dispersion of acceleration-type measure of near-fault ground motion is the least, and it is suggested that peak ground acceleration (PGA) and spectral acceleration (Sa) in the acceleration-type measures should be selected as the intensity measures of ground motion. The back propagation (BP) neural network can be used to effectively predict the seismic damage of utility tunnel structure with the calculated data by finite element method as samples, and the PGA, Sa and shear modulus of soil all have great influence on the seismic fragility of utility tunnel. Meanwhile, the exceedance probability gradually decreases with the increase of the shear modulus of soil. The variation range of exceedance probability at Life Safety (LS) or Collapse Prevention (CP) performance level is significantly greater than that at Operational (OP) or Immediate Occupancy (IO) performance level. Considering that double parameters of PGA and Sa can more accurately reflect the effect of the different ground motion parameters on structural damage, and considering single parameter of PGA or Sa may overestimate the damage degree of structures, it is suggested that both PGA and Sa should be considered for the analysis of seismic fragility of shallow buried underground structures such as utility tunnel.
- utility tunnel /
- near-fault ground motion /
- seismic fragility /
- intensity measure /
- BP neural network

HTML全文

历次地震中不乏地下综合管廊震害实例^[1]，为此，诸多学者从地震输入^[2-5]、结构体系^[6-10]、工程场地^[11-13]等方面研究了地下综合管廊的地震响应，袁勇等^[14]进一步对目前综合管廊抗震分析研究进展进行了总结评述。众所周知，结构地震易损性分析有助于更早发现潜在风险并采取相应措施。因此，综合管廊等地下结构地震易损性研究也取得较为丰富的成果，如地铁车站^[15-20]、隧道^[21-25]、综合管廊^[26]等。

针对地铁车站，HUH等^[15]以地面峰值加速度(Peak Ground Acceleration, PGA)作为地震动强度指标(Intensity Measure, IM)，以柱端塑性铰作为结构损伤指标(Damage Measure, DM)，研究分析了浅埋两层箱形结构的地震易损性；钟紫蓝等^[16-18]采用增量动力分析(Incremental Dynamic Analysis，IDA)方法对地铁车站进行易损性分析，认为对于浅埋结构，地表PGA宜为IM；陈之毅等^[19]基于深度学习方法提出一种地震响应概率模型，采用正交化IM选用贡献率最大的5个相互正交主成分以此评价地铁车站易损性；JIANG等^[20]采用IDA方法进行了地铁车站地震易损性研究，结果表明：近场地震动对地铁车站具有更高的破坏概率。

针对隧道，王伯超等^[21]采用IDA方法对公路隧道进行易损性分析，认为PGA宜作为IM；NGUYEN等^[22]以弯矩比为DM，通过分析箱形隧道结构的易损性，建议采用PGV/V_s30作为IM；HUANG等^[23]综合考虑PGA和PGV，采用IDA方法计算分析了软土隧道的地震易损性，并进一步采用人工神经网络进行了研究，结果表明：PGV宜作为IM^[24]；SILVA等^[25]采用有限差分法研究了软土隧道的地震易损性，研究表明，PGA相关度最高。

针对综合管廊，张景威等^[26]以PGA为IM，以节点位移为DM，输入多条随机地震动进行非线性动力时程分析，研究了不同强度地震动作用下地下综合管廊结构的易损性。

由上述研究可知，目前地下结构地震易损性研究大多采用单一IM，且主要以PGA为主；不同结构体系的抗震薄弱位置不同，DM的选取也不尽相同。目前综合管廊损伤状态的判定尚缺乏明确的规范要求，而且对于近断层地震动作用下综合管廊地震易损性的研究仍比较匮乏。因此，本文针对地下双层综合管廊，以最大层间位移角作为DM，采用IDA方法^[27]进行结构地震易损性分析，从而为近断层地震动作用下综合管廊地震损伤预测提供参考。

1 数值模型与地震输入

1.1 数值模型

图1为地下综合管廊场地模型示意图^[28]。利用ABAQUS建立土-综合管廊三维有限元模型^[29-30]，模型上表面为自由边界，两侧及底面均采用粘弹性边界^[31]，地震输入则通过等效节点力在边界输入^[32]。其中，土体和管廊均采用C3D8R单元，钢筋采用T3D2单元进行模拟；土体选用Mohr-Coulomb本构模型，C35混凝土选用损伤塑性模型(Concrete Damaged Plasticity, CDP)；钢筋选用HRB335，采用无屈服点弹塑性本构模型；接触采用ABAQUS自带的面与面接触，法向为Hard，切向为Penalty，摩擦系数为0.4。具体材料参数见表1。

图 1 地下综合管廊模型　/mm

Figure 1. The model of underground utility tunnel

下载: 全尺寸图片幻灯片

表 1 材料参数

Table 1. Material parameters

混凝土	密度/( ${\text{kg/}}{{\text{m}}^{\text{3}}}$ )	弹性模量/GPa	泊松比	膨胀角/(°)	偏心率	${\sigma _{{\text{b0}}}}{\text{/}}{\sigma _{{\text{c0}}}}$	${K_{\text{c}}}$
混凝土	2400	31.5	0.167	15	0.1	1.16	0.66667
土体	密度/( ${\text{kg/}}{{\text{m}}^{\text{3}}}$ )	弹性模量/MPa	泊松比	摩擦角/(°)	膨胀角/(°)	粘聚力/kPa	阻尼比
土体	1900	129	0.35	27.8	13.9	35	0.06
钢筋	密度/( ${\text{kg/}}{{\text{m}}^{\text{3}}}$ )	弹性模量/GPa	泊松比	屈服强度/MPa	峰值应变		极限强度/MPa
钢筋	7800	200	0.3	400	0.075		460

下载: 导出CSV

| 显示表格

1.2 地震输入

参考黄景琦等^[33]关于斜入射地震波对地铁车站结构的不利影响，本文分析地下综合管廊在30度斜入射SV波作用下的动力响应。

根据场地条件、地震动强度、震中距大小为主要参考指标，参考FEMA P-58-1^[34]从太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center, PEER)选取了12条近断层地震动记录^[35](表2)，其加速度反应谱曲线如图2所示。首先对12条地震波进行截波及基线校正，而后进行调幅：①对峰值加速度(PGA)按比例调整为0.1 g~1.0 g(g=9.8 m/s²)范围内10个不同峰值的地震动；②对谱加速度(S_a)按比例调整为0.3 g~3.0 g范围内10个不同峰值的地震动，最后分别将240条调幅地震波作为地震输入进行增量动力分析。

表 2 近断层地震动记录

Table 2. Near-fault ground motion records

编号	台站	PGA/g	震级Mw	震中距/km	地点
01	RSN161-Brawley Airport	0.152	6.53	10.42	Imperial Valley-06
02	RSN178-El Centro Array #3	0.127	6.53	12.85	Imperial Valley-06
03	RSN179-El Centro Array #4	0.269	6.53	7.05	Imperial Valley-06
04	RSN185-Holtville Post Office	0.257	6.53	7.50	Imperial Valley-06
05	RSN292-Sturno(STN)	0.225	6.90	10.84	Irpinia-Italy-01
06	RSN764-Gilroy-Historic Bldg	0.148	6.93	10.97	Loma Prieta
07	RSN766-Gilroy Array #2	0.295	6.93	11.07	Loma Prieta
08	RSN1050-Pacoima Dam (downstr)	0.191	6.69	7.01	Northridge-01
09	RSN1052-Pacoima Kagel Canyon	0.169	6.69	7.26	Northridge-01
10	RSN1165-Izmit	0.144	7.51	7.21	Kocaeli Turkey
11	RSN3746-Centerville BeachNaval Fac	0.121	7.01	18.31	Cape Mendocino
12	RSN4458-Ulcinj-Hotel Olimpic	0.423	7.10	5.76	Montenegro Yugoslavia

下载: 导出CSV

| 显示表格

图 2 近断层地震动加速度反应谱

Figure 2. Acceleration response spectra of near-fault ground motion

下载: 全尺寸图片幻灯片

2 地下综合管廊的易损性分析

2.1 地震动强度指标选取与抗震性能水平划分

地震动强度指标(IM)的选取在一定程度上决定了易损性分析的结果是否可靠^[17]，本文选取加速度型、速度型及位移型三类共计9种地震动强度指标，即地面峰值加速度(PGA)、谱加速度(Sa)、均方根加速度(A_rms)、地面峰值速度(PGV)、谱速度(Sv)、均方根速度(V_rms)、地面峰值位移(PGD)、谱位移(Sd)和均方根位移(D_rms)。通过对比其作为地震动强度指标时对IDA分析结果的离散性，确定出最合理的地震动强度指标^[26]。本文选用层间位移角最大值 ${\theta _{\max }}$ 作为DM。

根据结构损伤指标和地震动强度指标近似满足幂函数关系^[36]，进行对数线性回归并计算标准差。给出了9种地震动强度指标对应的标准差 ${\beta _{\text{D}}}$ ，可以看出，加速度型指标的离散性小于速度型指标小于位移型指标，因此，本文易损性分析选用PGA和Sa作为IM。

表 3 地震动强度参数标准差

Table 3. Standard deviation of parameters of ground motion intensity

地震动强度指标IM	地面峰值加速度PGA	地面峰值速度PGV	地面峰值位移PGD	谱加速度Sa	谱速度Sv	谱位移Sd	均方根加速度A_rms	均方根速度V_rms	均方根位移D_rms
${\beta _{\text{D}}}$	0.21	0.41	0.87	0.25	0.36	0.69	0.28	0.52	0.86

下载: 导出CSV

| 显示表格

将地下结构的抗震性能水平划分为四级^{[26, 34]}，即基本完好(OP)、轻微损坏(IO)、生命安全(LS)和防止倒塌(CP)。采用Pushover法对综合管廊不同性能水平所对应的层间位移角限值进行标定^[37-38]，可得到四个性能水平对应的层间位移角限值分别为0.000 31、0.000 45、0.001 26和0.002 28。

2.2 以PGA或Sa为IM的综合管廊易损性分析

浅埋地下结构地震易损性曲线近似服从对数正态分布^{[18, 39-40]}，即结构响应超越性能水平极限值的超越概率可表示为：

${P_{\rm{f}}}({d_{\rm S}} {\geqslant} {d_{{\rm S}i}}\left| S \right.) = \varPhi \left[\frac{1}{{{\beta _{{\text{tot}}}}}}\ln \left(\frac{S}{{{S_{{{{\rm m}i}}}}}}\right)\right]$

(1)

式中： ${d_{\rm S}}$ 为在给定地震动强度S下结构的地震响应； ${d_{{\rm S}i}}$ 为结构性能水准的临界值； ${S_{{{{\rm m}i}}}}$ 为结构处于某个性能水平限值； ${\beta _{{\text{tot}}}}$ 为总的对数正态标准偏差。

经过一元线性回归分析得到基于PGA或Sa的易损性分析回归方程为：

$\ln ({\theta _{\max }}) = 1.1637\ln ({\text{PGA}}) - 5.7871$

(2)

$\ln ({\theta _{\max }}) = 0.9648\ln ({\text{Sa}}) - 7.1035 \;\;\;\;$

(3)

将不同地震动的PGA和Sa分别代入式(2)和式(3)，再根据式(1)计算超越概率。

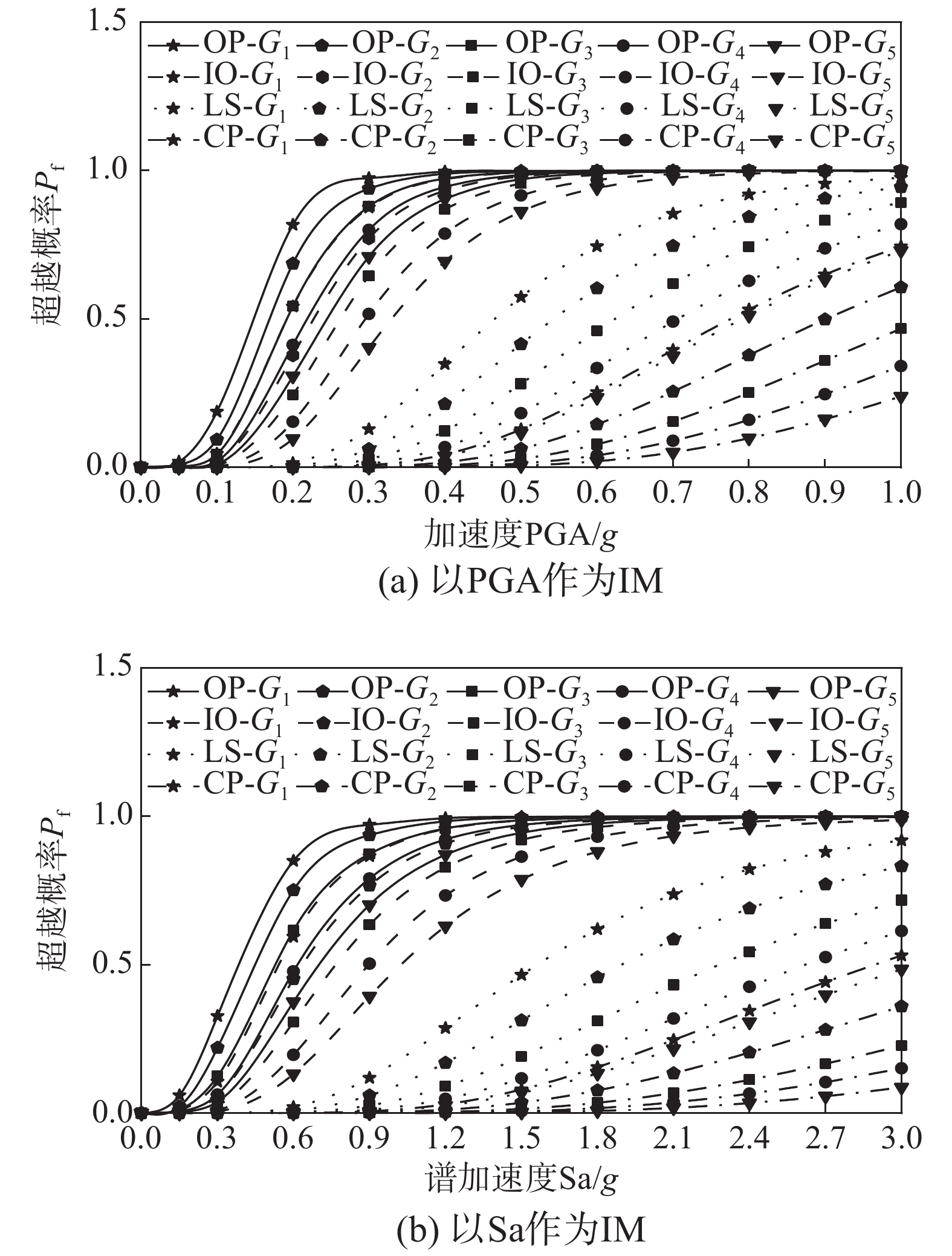
图3给出了不同抗震性能水平下的综合管廊结构地震易损性曲线。根据前文定义的四级性能水平指标，可将综合管廊结构的损伤状态划分为五个等级，即基本完好、轻微破坏、中等破坏、严重破坏、倒塌。可以看出，结构易损性曲线的形状随着结构损伤状态的严重而呈现平缓的趋势；随着PGA或Sa的增大，综合管廊的各个性能水平的超越概率也逐渐增大，当PGA<0.3 g或S_a<0.9 g时，OP和IO状态下易损性曲线比较陡峭，超越概率快速增大，表明综合管廊的破坏向着更为严重的状态发展。

图 3 以PGA或Sa为IM的综合管廊结构地震易损性曲线

Figure 3. Seismic fragility curve of utility tunnel structure with PGA or Sa as IM

下载: 全尺寸图片幻灯片

2.3 基于神经网络的综合管廊易损性分析

当分别考虑峰值加速度、土体剪切模量等多个参数对综合管廊结构易损性的影响时，采用有限元计算综合管廊地震响应则需要大量的计算耗时，因此，以有限元计算数据为训练样本，基于BP神经网络来预测综合管廊的地震损伤，则不失为一种简捷高效方法。众所周知，神经网络在预测过程中会存在不确定性，但从整体来看，相关性随训练数据集的增加而逐渐增加^[41]。

表4给出了输入参数即地震动强度指标PGA、Sa及土体剪切模量G选取的基准值和变化范围，通过训练完成后的神经网络模型对各工况下的层间位移角进行预测。本文将600个样本集作为训练数据，随机分配为训练集和测试集。其中，480个样本作为训练集供神经网络进行学习，120个样本作为测试集用来测试神经网络的训练精度，训练数据集占比为80%。

表 4 输入参数的基准值和变化范围

Table 4. The reference value and variation range of input parameter

输入参数	基准值	参数变化范围
PGA/g	${P_0} = 1.0$	0.1~1.0 ${P_0}$ ，系数增量为0.1
Sa/g	${S_0} = 3.0$	0.1~1.0 ${S_0}$ ，系数增量为0.1
G/kPa	${G_0} = 8 \times {10^4}$	0.6~1.4 ${G_0}$ ，系数增量为0.2

下载: 导出CSV

| 显示表格

将PGA、Sa及土体剪切模量G三个影响因素作为输入参数，用于反映地震动不确定性及场地不确定性^[42]，将有限元计算得到的综合管廊层间位移角最大值作为输出参数，建立包含输入层、隐含层和输出层的三层神经网络，网络模型参数为：① 输入层含3个节点，输出层含1个节点，隐含层含10个节点；② 最大迭代步数为1000步；③ 学习速率设置为0.01；④ 误差容许值为0.0001；⑤ 动量常数设置为0.5。基于以上参数对神经网络进行训练，训练的归一化结果如图4所示。通过实际值与预测值进行拟合分别得到3条拟合曲线，虚线为理想条件下实际值与预测值相等的情况，结果表明，训练、测试及所有样本数据的相关系数均在0.9以上，拟合效果较好，建立的关系模型可靠。

图 4 BP神经网络回归结果

Figure 4. Regression results derived by BP neural network

下载: 全尺寸图片幻灯片

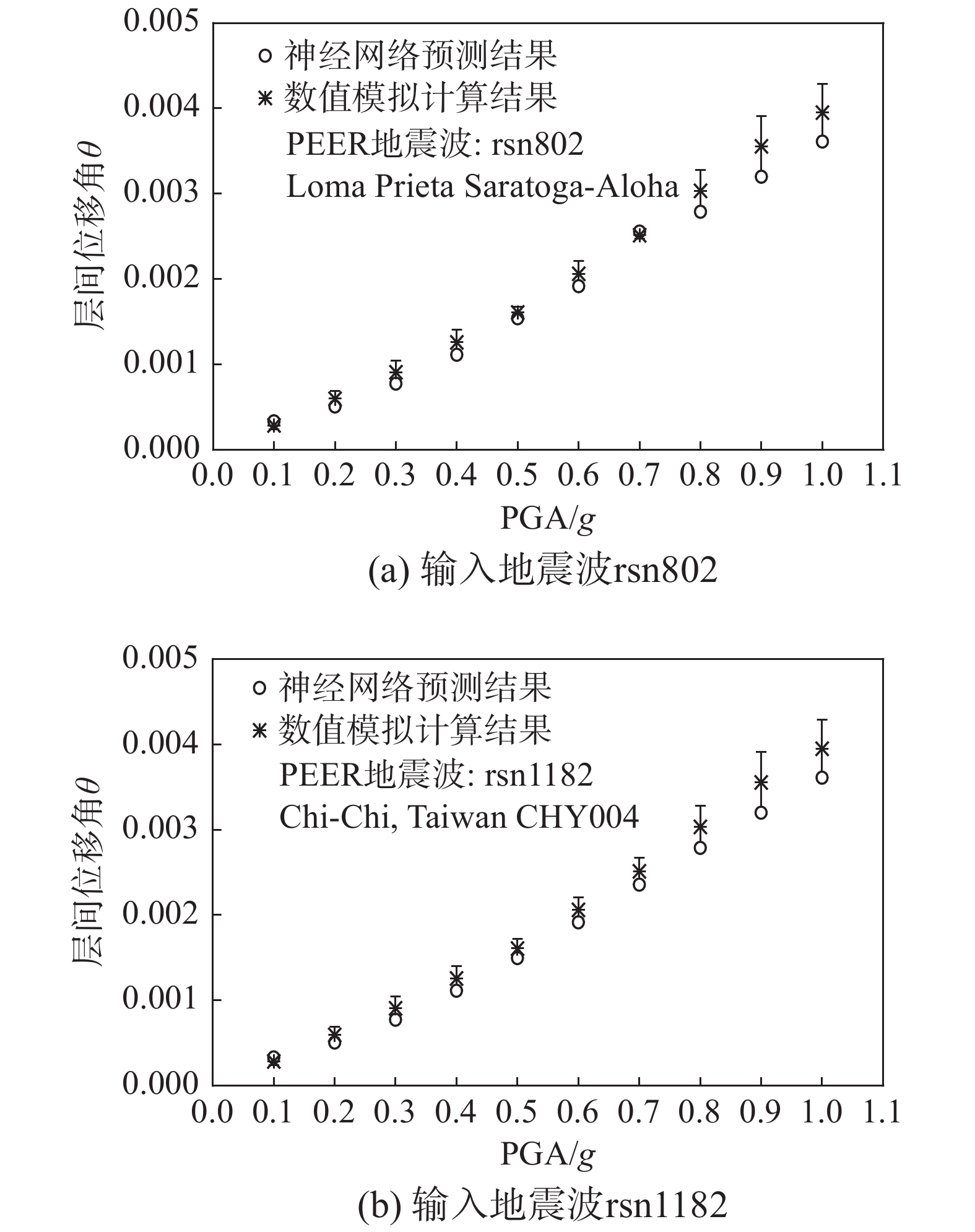
图5给出了神经网络预测值与有限元计算值(输入其它地震波)的对比。其中，神经网络预测值与有限元计算值最大相对误差为16.57%，神经网络的预测值与实际值误差不大，训练结果较为良好，能够在一定程度预测计算结果，可以作为地下综合管廊易损性分析的辅助工具进行初步评估。

图 5 BP神经网络预测值与有限元计算值对比

Figure 5. Comparison between the predictive values by BP neural network and the ones calculated by FEM

下载: 全尺寸图片幻灯片

图6给出了由神经网络预测数据计算得出的易损性曲线。可以看出，土体剪切模量对易损性曲线的影响非常显著，随着土体剪切模量的增大，超越概率变化区间范围增大。土体剪切模量对OP、IO损伤状态的影响明显小于LS、CP两种损伤状态，OP、IO状态下易损性曲线较为陡峭，说明此状态易达到；在OP状态下，当地震动峰值加速度超过0.5 g时，五种场地土对应的结构超越概率均趋于1，管廊不能保持OP状态；在IO状态下，只有地震动强度足够大(约超0.7 g)时，五种场地土对应的结构超越概率方趋于1，管廊不能保持IO状态，向更严重的破坏状态发展。LS、CP的易损性曲线较为平缓，结构进入塑性变形阶段，当地震动强度一定时，随着土体剪切模量的增大，超越概率逐渐减小(表5)，说明场地土越硬，对结构抗震越有利。因此，实际工程选址时应充分结合现场勘查确定所选场地是否合理。

图 6 不同场地土对应的综合管廊结构地震易损性曲线

Figure 6. Seismic fragility curve of utility tunnel structure for different site soils

下载: 全尺寸图片幻灯片

表 5 不同场地土对应的综合管廊LS、CP状态超越概率

Table 5. Exceedance probability of utility tunnel at LS and CP states for different site soils /(%)

PGA/g	损伤状态	G₁(0.6G₀)	G₂(0.8G₀)	G₃(1.0G₀)	G₄(1.2G₀)	G₅(1.4G₀)
0.6	LS	74.5	60.3	46.0	33.5	23.5
0.6	CP	25.3	14.5	7.7	4.0	2.0
0.8	LS	91.9	84.4	74.3	62.8	51.2
0.8	CP	53.2	37.8	25.2	16.0	9.8
1.0	LS	97.6	94.4	89.2	81.9	73.0
1.0	CP	74.4	60.7	46.7	34.1	23.9

下载: 导出CSV

| 显示表格

2.4 以PGA和Sa为IM的综合管廊易损性分析

以PGA和Sa作为地震动强度指标，分别记为IM₁=im₁和IM₂=im₂， ${\theta _{\max }}$ 为结构损伤指标。对其进行回归分析得到：

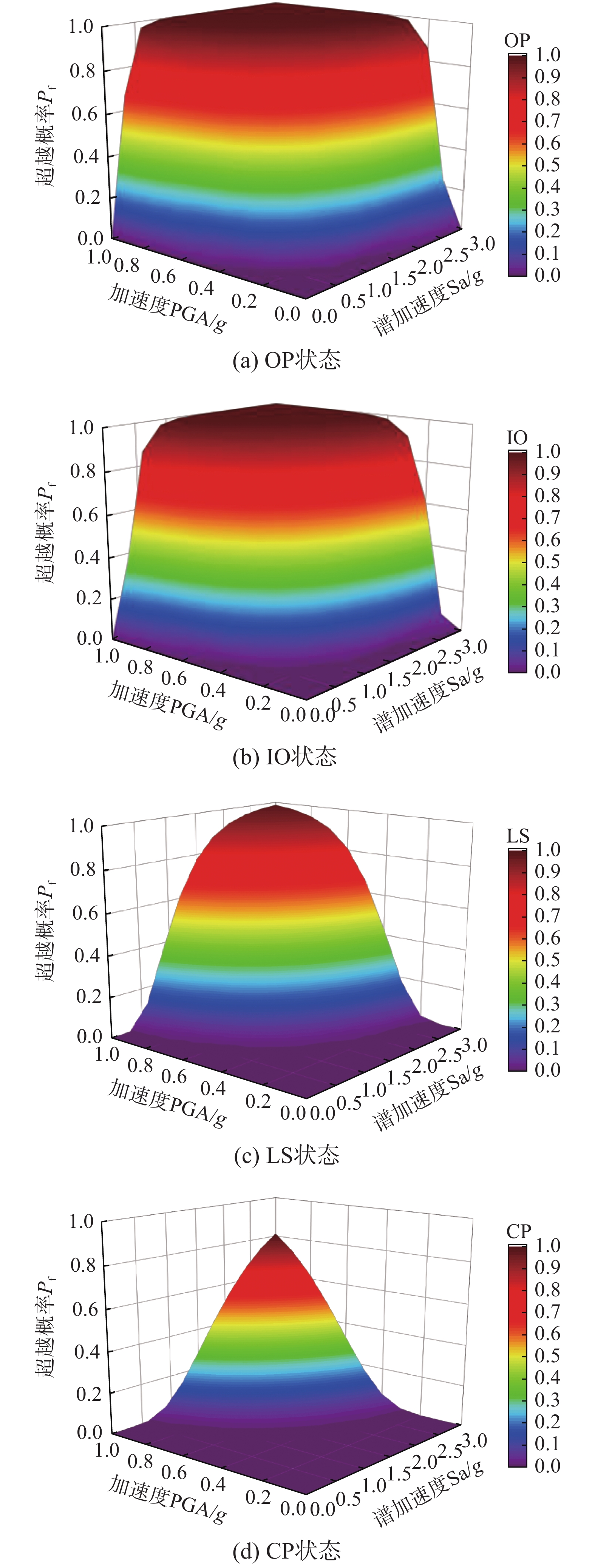
$\ln ({\theta _{\max }}) = 1.1569\ln ({\text{PGA}}) + 0.9549\ln ({S_{\rm a}}) - 6.7254$

(4)

${P_{\rm{f}}}({d_{\rm S}} {\geqslant} {d_{{\rm S}i}}\left| S \right.) = \varPhi \left[\frac{1}{{{\beta _{{\text{tot}}}}}}\ln \left(\frac{{S\left| {{\text{i}}{{\text{m}}_1},{\text{i}}{{\text{m}}_2}} \right.}}{{{S_{{{{\rm m}i}}}}}}\right)\right]$

(5)

将不同地震动的PGA和Sa代入式(4)得出 ${\theta _{\max }}$ ，而后根据式(5)计算超越概率，得到不同性能水平下的易损性曲面(图7)。从图7可以看出，随着地震动强度PGA、Sa的逐渐增大，超越概率不断增大。四种不同损伤状态下两侧易损性曲线陡峭程度也很相似，说明PGA和Sa对综合管廊超越概率的影响程度也相似。值得一提的是，地震动强度指标PGA、Sa及土体剪切模量G的变化对易损性分析的敏感度贡献分别为37.89%、34.99%、27.12%。

图 7 以PGA和Sa为IM的综合管廊结构地震易损性曲面

Figure 7. Structural fragility surface of utility tunnel with both PGA and Sa as IM

下载: 全尺寸图片幻灯片

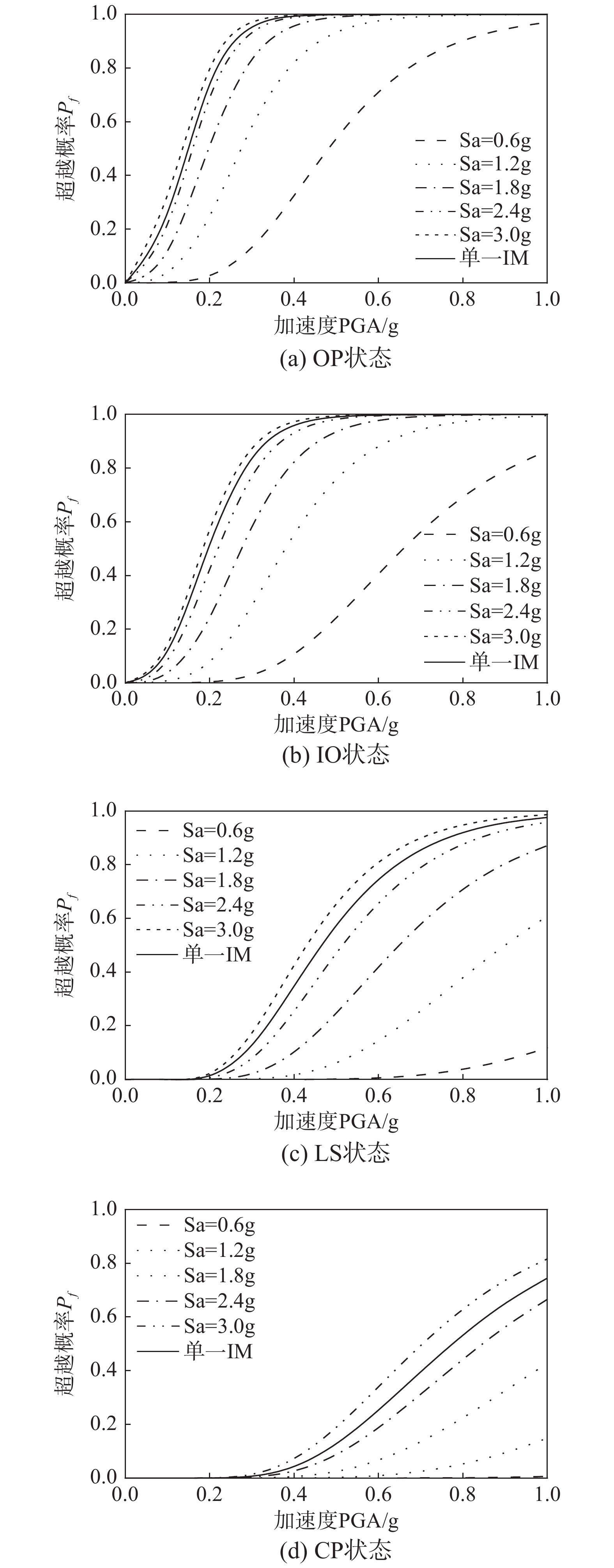
图8给出了Sa=0.6 g、1.2 g、1.8 g、2.4 g及3.0 g时的综合管廊结构地震易损性曲线。可以看出，超越概率随着Sa的增大而增大，而单一IM对应的超越概率较大，显然，忽略Sa的影响有可能高估结构的损伤。当PGA=0.11 g时(多遇地震)管廊受到轻微破坏的最大概率为18.12%，倒塌概率为0，管廊能够保持OP状态；当PGA=0.3 g时(设防地震)管廊不能保持OP状态，当Sa大于1.2 g时管廊超越IO状态概率在60%以上，管廊易达到轻微损伤，在LS状态下仅当Sa为3.0 g左右时管廊超越概率为17.36%，在设防地震作用下基本达不到CP状态；当PGA=0.51 g时(罕遇地震)管廊均不能保持OP、IO状态，在LS状态下Sa=2.4 g和3.0 g时管廊发生严重破坏的概率分别为48.92%和67.13%，管廊发生严重破坏可能性较大，应重点关注，在CP状态下，Sa小于2.4 g时管廊相对安全，当Sa在3.0 g左右时管廊发生倒塌的概率为20.29%。因此，为准确评估地下结构的抗震性能，建议地下结构易损性分析应综合考虑PGA和Sa的影响。

下载: 全尺寸图片幻灯片

8 Sa不同时的综合管廊结构地震易损性曲线

8. Seismic fragility curve of utility tunnel structure for different Sa

下载: 全尺寸图片幻灯片

3 结论

本文以近断层地震动为输入，采用有限元法对浅埋双层综合管廊进行非线性动力时程分析，并采用IDA方法进行结构易损性分析，给出不同地震动强度下浅埋双层综合管廊结构的破坏概率，为综合管廊等地下结构的地震损伤预测提供参考。相关研究结论如下：

(1) 地震动强度指标的离散性：加速度型指标＜速度型指标＜位移型指标，建议进行综合管廊等浅埋地下结构地震易损性分析时，选取加速度型指标PGA、Sa作为地震动强度指标。

(2) PGA、Sa及土体剪切模量对综合管廊结构地震易损性分析结果影响明显，随着土体剪切模量的增大，超越概率逐渐减小，且LS、CP状态超越概率变化范围要明显大于OP、IO状态。值得一提的是，神经网络预测具有较高的可靠性(90%以上)，可对综合管廊等地下结构地震损伤进行快速预测。

(3) 考虑PGA和Sa双参数的地震易损性分析能综合反映不同地震动强度指标对结构损伤超越概率的影响，而相比之下，仅考虑PGA或Sa单参数影响所得出的超越概率偏大，可能高估结构损伤程度。因此，在综合管廊等浅埋地下结构地震易损性分析中，建议同时考虑PGA和Sa的影响。

图 1 地下综合管廊模型　/mm

Figure 1. The model of underground utility tunnel

下载: 全尺寸图片幻灯片

图 2 近断层地震动加速度反应谱

Figure 2. Acceleration response spectra of near-fault ground motion

下载: 全尺寸图片幻灯片

图 3 以PGA或Sa为IM的综合管廊结构地震易损性曲线

Figure 3. Seismic fragility curve of utility tunnel structure with PGA or Sa as IM

下载: 全尺寸图片幻灯片

图 4 BP神经网络回归结果

Figure 4. Regression results derived by BP neural network

下载: 全尺寸图片幻灯片

图 5 BP神经网络预测值与有限元计算值对比

Figure 5. Comparison between the predictive values by BP neural network and the ones calculated by FEM

下载: 全尺寸图片幻灯片

图 6 不同场地土对应的综合管廊结构地震易损性曲线

Figure 6. Seismic fragility curve of utility tunnel structure for different site soils

下载: 全尺寸图片幻灯片

图 7 以PGA和Sa为IM的综合管廊结构地震易损性曲面

Figure 7. Structural fragility surface of utility tunnel with both PGA and Sa as IM

下载: 全尺寸图片幻灯片

8 Sa不同时的综合管廊结构地震易损性曲线

8. Seismic fragility curve of utility tunnel structure for different Sa

下载: 全尺寸图片幻灯片

表 1 材料参数

Table 1 Material parameters

混凝土	密度/( ${\text{kg/}}{{\text{m}}^{\text{3}}}$ )	弹性模量/GPa	泊松比	膨胀角/(°)	偏心率	${\sigma _{{\text{b0}}}}{\text{/}}{\sigma _{{\text{c0}}}}$	${K_{\text{c}}}$
混凝土	2400	31.5	0.167	15	0.1	1.16	0.66667
土体	密度/( ${\text{kg/}}{{\text{m}}^{\text{3}}}$ )	弹性模量/MPa	泊松比	摩擦角/(°)	膨胀角/(°)	粘聚力/kPa	阻尼比
土体	1900	129	0.35	27.8	13.9	35	0.06
钢筋	密度/( ${\text{kg/}}{{\text{m}}^{\text{3}}}$ )	弹性模量/GPa	泊松比	屈服强度/MPa	峰值应变		极限强度/MPa
钢筋	7800	200	0.3	400	0.075		460

下载: 导出CSV

表 2 近断层地震动记录

Table 2 Near-fault ground motion records

编号	台站	PGA/g	震级Mw	震中距/km	地点
01	RSN161-Brawley Airport	0.152	6.53	10.42	Imperial Valley-06
02	RSN178-El Centro Array #3	0.127	6.53	12.85	Imperial Valley-06
03	RSN179-El Centro Array #4	0.269	6.53	7.05	Imperial Valley-06
04	RSN185-Holtville Post Office	0.257	6.53	7.50	Imperial Valley-06
05	RSN292-Sturno(STN)	0.225	6.90	10.84	Irpinia-Italy-01
06	RSN764-Gilroy-Historic Bldg	0.148	6.93	10.97	Loma Prieta
07	RSN766-Gilroy Array #2	0.295	6.93	11.07	Loma Prieta
08	RSN1050-Pacoima Dam (downstr)	0.191	6.69	7.01	Northridge-01
09	RSN1052-Pacoima Kagel Canyon	0.169	6.69	7.26	Northridge-01
10	RSN1165-Izmit	0.144	7.51	7.21	Kocaeli Turkey
11	RSN3746-Centerville BeachNaval Fac	0.121	7.01	18.31	Cape Mendocino
12	RSN4458-Ulcinj-Hotel Olimpic	0.423	7.10	5.76	Montenegro Yugoslavia

下载: 导出CSV

表 3 地震动强度参数标准差

Table 3 Standard deviation of parameters of ground motion intensity

地震动强度指标IM	地面峰值加速度PGA	地面峰值速度PGV	地面峰值位移PGD	谱加速度Sa	谱速度Sv	谱位移Sd	均方根加速度A_rms	均方根速度V_rms	均方根位移D_rms
${\beta _{\text{D}}}$	0.21	0.41	0.87	0.25	0.36	0.69	0.28	0.52	0.86

下载: 导出CSV

表 4 输入参数的基准值和变化范围

Table 4 The reference value and variation range of input parameter

输入参数	基准值	参数变化范围
PGA/g	${P_0} = 1.0$	0.1~1.0 ${P_0}$ ，系数增量为0.1
Sa/g	${S_0} = 3.0$	0.1~1.0 ${S_0}$ ，系数增量为0.1
G/kPa	${G_0} = 8 \times {10^4}$	0.6~1.4 ${G_0}$ ，系数增量为0.2

下载: 导出CSV

表 5 不同场地土对应的综合管廊LS、CP状态超越概率

Table 5 Exceedance probability of utility tunnel at LS and CP states for different site soils /(%)

PGA/g	损伤状态	G₁(0.6G₀)	G₂(0.8G₀)	G₃(1.0G₀)	G₄(1.2G₀)	G₅(1.4G₀)
0.6	LS	74.5	60.3	46.0	33.5	23.5
0.6	CP	25.3	14.5	7.7	4.0	2.0
0.8	LS	91.9	84.4	74.3	62.8	51.2
0.8	CP	53.2	37.8	25.2	16.0	9.8
1.0	LS	97.6	94.4	89.2	81.9	73.0
1.0	CP	74.4	60.7	46.7	34.1	23.9

下载: 导出CSV

参考文献(42)

[1]	刘述虹. 典型综合管廊体系地震响应分析[D]. 哈尔滨: 中国地震局工程力学研究所, 2016. LIU Shuhong. Seismic response analysis of typical urban utility tunnel system [D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2016. (in Chinese)
[2]	岳庆霞, 李杰. 地下综合管廊地震响应研究[J]. 同济大学学报(自然科学版), 2009, 37(3): 285 − 290. YUE Qingxia, LI Jie. Research on utility tunnel seismic response [J]. Journal of Tongji University (Natural Science), 2009, 37(3): 285 − 290. (in Chinese)
[3]	蒋录珍, 李杰, 陈隽. 非一致地震激励下综合管廊接头响应数值模拟[J]. 世界地震工程, 2015, 31(2): 101 − 107. JIANG Luzhen, LI Jie, CHEN Jun. Numerical simulation of utility tunnel joint effects under non-uniform earthquake excitation [J]. World Earthquake Engineering, 2015, 31(2): 101 − 107. (in Chinese)
[4]	KONSTANDAKOPOULOU F D, BESKOU N D, HATZIGEORGIOU G D. Three-dimensional nonlinear response of utility tunnels under single and multiple earthquakes [J]. Soil Dynamics and Earthquake Engineering, 2021, 143: 106607. doi: 10.1016/j.soildyn.2021.106607
[5]	施有志, 华建兵, 阮建凑, 等. 地下综合管廊地震动力响应三维数值分析[J]. 工程地质学报, 2018, 26(3): 785 − 793. SHI Youzhi, HUA Jianbing, RUAN Jiancou, et al. Three dimensional numerical analysis of dynamic response of underground utility tunnels during earthquake [J]. Journal of Engineering Geology, 2018, 26(3): 785 − 793. (in Chinese)
[6]	汤爱平, 李志强, 冯瑞成, 等. 共同沟结构体系振动台模型试验与分析[J]. 哈尔滨工业大学学报, 2009, 41(6): 1 − 5. doi: 10.3321/j.issn:0367-6234.2009.06.001 TANG Aiping, LI Zhiqiang, FENG Ruicheng, et al. Model experiment and analysis on seismic response of utility tunnel systems using a shaking table [J]. Journal of Harbin Institute of Technology, 2009, 41(6): 1 − 5. (in Chinese) doi: 10.3321/j.issn:0367-6234.2009.06.001
[7]	郭恩栋, 王鹏宇, 刘述虹, 等. 典型综合管廊体系的地震响应分析[J]. 地震工程与工程振动, 2018, 38(1): 124 − 134. GUO Endong, WANG Pengyu, LIU Shuhong, et al. Seismic response analysis of typical utility tunnel system [J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(1): 124 − 134. (in Chinese)
[8]	梁建文, 闫启超, 王长祥, 等. 地下T型交叉管廊的抗震时程分析[J]. 地震工程与工程振动, 2021, 41(2): 1 − 12. LIANG Jianwen, YAN Qichao, WANG Changxiang, et al. Seismic time-history analysis of T-type underground utility tunnels [J]. Earthquake Engineering and Engineering Dynamics, 2021, 41(2): 1 − 12. (in Chinese)
[9]	谷音, 邱诗榕, 熊梦婷, 等. 预制综合管廊-接头-场地土地震响应分析[J]. 建筑结构, 2022, 52(3): 57 − 66. GU Yin, QIU Shirong, XIONG Mengting, et al. Seismic response analysis of prefabricated comprehensive pipe gallery-joint-site soil [J]. Building Structure, 2022, 52(3): 57 − 66. (in Chinese)
[10]	钟紫蓝, 李广帆, 石少华, 等. 叠合板式综合管廊侧墙连接节点面外抗震性能试验研究[J]. 工程力学, 2023. doi: 10.6052/j.issn.1000-4750.2022.04.0313 ZHONG Zilan, LI Guangfan, SHI Shaohua, et al. Experimental study on out-of-plane seismic performance of sidewall connections of utility tunnels with composite plates [J]. Engineering Mechanics, 2023. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.04.0313
[11]	岳峰, 刘博文, 廖凯, 等. 非液化场地和可液化场地中预制装配式钢制波纹管综合管廊抗震性能振动台试验研究[J]. 建筑钢结构进展, 2022, 24(2): 105 − 110. YUE Feng, LIU Bowen, LIAO Kai, et al. Shaking table test study on prefabricated corrugated steel utility tunnels on non-liquefiable and liquefiable ground [J]. Progress in Steel Building Structures, 2022, 24(2): 105 − 110. (in Chinese)
[12]	黄德龙, 宗钟凌, 汤爱平, 等. 穿越非均匀土体综合管廊振动台试验研究[J]. 工程力学, 2023. doi: 10.6052/j.issn.1000-4750.2022.06.0538 HUANG Delong, ZONG Zhongling, TANG Aiping, et al. Shaking table experimental study of utility tunnel in non-homogeneous soil [J]. Engineering Mechanics, 2023. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.06.0538
[13]	黄子渊, 汤爱平, 黄德龙, 等. 非均匀场地节段预制综合管廊接头地震响应分析[J]. 特种结构, 2022, 39(1): 7 − 16. HUANG Ziyuan, TANG Aiping, HUANG Delong, et al. Seismic response of segmental prefabricated utility tunnel joints in heterogeneous field [J]. Special Structures, 2022, 39(1): 7 − 16. (in Chinese)
[14]	袁勇, 朱力, 禹海涛, 等. 综合管廊抗震分析研究进展综述[J]. 隧道建设, 2022, 42(11): 1821 − 1831. YUAN Yong, ZHU Li, YU Haitao, et al. Review on seismic analysis of utility tunnels [J]. Tunnel Construction, 2022, 42(11): 1821 − 1831. (in Chinese)
[15]	HUH J, TRAN Q H, HALDAR A, et al. Seismic vulnerability assessment of a shallow two-story underground RC box structure [J]. Applied Sciences, 2017, 7(7): 735. doi: 10.3390/app7070735
[16]	钟紫蓝, 申轶尧, 郝亚茹, 等. 基于IDA方法的两层三跨地铁地下结构地震易损性分析[J]. 岩土工程学报, 2020, 42(5): 916 − 924. ZHONG Zilan, SHEN Yiyao, HAO Yaru, et al. Seismic fragility analysis of two-story and three-span metro station structures based on IDA method [J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 916 − 924. (in Chinese)
[17]	钟紫蓝, 严智豪, 史跃波, 等. 基于IDA方法的地铁车站结构抗震性能评价[J]. 北京工业大学学报, 2021, 47(7): 680 − 690. ZHONG Zilan, YAN Zhihao, SHI Yuebo, et al. Seismic performance evaluation of station structures based on IDA method [J]. Journal of Beijing University of Technology, 2021, 47(7): 680 − 690. (in Chinese)
[18]	ZHONG Z L, SHEN Y Y, ZHAO M, et al. Seismic fragility assessment of the Daikai subway station in layered soil [J]. Soil Dynamics and Earthquake Engineering, 2020, 132: 106044. doi: 10.1016/j.soildyn.2020.106044
[19]	陈之毅, 黄鹏飞. 基于概率神经网络的地铁车站易损性分析[J]. 同济大学学报(自然科学版), 2021, 49(6): 791 − 798. CHEN Zhiyi, HUANG Pengfei. Fragility analysis of a subway station based on probability artificial neural network [J]. Journal of Tongji University (Natural Science), 2021, 49(6): 791 − 798. (in Chinese)
[20]	JIANG J W, EL NGGAR H M, XU C S, et al. Effect of ground motion characteristics on seismic fragility of subway station [J]. Soil Dynamics and Earthquake Engineering, 2021, 143: 106618. doi: 10.1016/j.soildyn.2021.106618
[21]	王伯超, 王鑫, 杨柳君, 等. 基于IDA分析法的公路隧道衬砌抗震性能分析[J]. 铁道标准设计, 2020, 64(5): 96 − 102. WANG Bochao, WANG Xin, YANG Liujun, et al. Seismic performance analysis of highway tunnel lining based on IDA [J]. Railway Standard Design, 2020, 64(5): 96 − 102. (in Chinese)
[22]	NGUYEN D D, PARK D, SHAMSHER S, et al. Seismic vulnerability assessment of rectangular cut-and-cover subway tunnels [J]. Tunnelling and Underground Space Technology, 2019, 86: 247 − 261. doi: 10.1016/j.tust.2019.01.021
[23]	HUANG Z K, PITILAKIS K, TSINIDIS G, et al. Seismic vulnerability of circular tunnels in soft soil deposits: The case of Shanghai metropolitan system [J]. Tunnelling and Underground Space Technology, 2020, 98: 103341. doi: 10.1016/j.tust.2020.103341
[24]	HUANG Z K, ARGYROUDIS S A, PITILAKIS K, et al. Fragility assessment of tunnels in soft soils using artificial neural networks [J]. Underground Space, 2022, 7(2): 242 − 253. doi: 10.1016/j.undsp.2021.07.007
[25]	SILVA F D, FABOZZI S, NIKITAS N, et al. Seismic vulnerability of circular tunnels in sand [J]. Géotechnique, 2021, 71(11): 1056 − 1070.
[26]	张景威, 周晶. 地下综合管廊结构的易损性分析[J]. 水利与建筑工程学报, 2018, 16(3): 48 − 53. ZHANG Jingwei, ZHOU Jing. Vulnerability analysis of underground utility tunnel [J]. Journal of Water Resources and Architectural Engineering, 2018, 16(3): 48 − 53. (in Chinese)
[27]	VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis [J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 491 − 514.
[28]	戴超, 张佩兰, 仲崇军. 双层管廊的工程应用及设计方案探讨[J]. 给水排水, 2018, 44(5): 109 − 113. DAI Chao, ZHANG Peilan, ZHONG Chongjun. Discussion on engineering application and design scheme of double-deck utility tunnel [J]. Water & Wastewater Engineering, 2018, 44(5): 109 − 113. (in Chinese)
[29]	XU Z G, DU X L, XU C S, et al. Numerical research on seismic response characteristics of shallow buried rectangular underground structure [J]. Soil Dynamics and Earthquake Engineering, 2019, 116: 242 − 252. doi: 10.1016/j.soildyn.2018.10.030
[30]	MA C, LU D C, DU X L, et al. Seismic performance upgrading for underground structures by introducing sliding isolation bearings [J]. Tunnelling and Underground Space Technology, 2018, 74: 1 − 9. doi: 10.1016/j.tust.2018.01.007
[31]	刘晶波, 谷音, 杜义欣. 一致粘弹性人工边界及粘弹性边界单元[J]. 岩土工程学报, 2006, 28(9): 1070 − 1075. LIU Jingbo, GU Yin, DU Yixin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070 − 1075. (in Chinese)
[32]	黄景琦. 岩体隧道非线性地震响应分析[D]. 北京: 北京工业大学, 2015. HUANG Jingqi. Study on nonlinear seismic response of rock tunnels [D]. Beijing: Beijing University of Technology, 2015. (in Chinese)
[33]	黄景琦, 杜修力, 田志敏, 等. 斜入射SV波对地铁车站地震响应的影响[J]. 工程力学, 2014, 31(9): 81 − 88, 103. doi: 10.6052/j.issn.1000-4750.2013.03.0278 HUANG Jingqi, DU Xiuli, TIAN Zhimin, et al. Effect of the oblique incidence of seismic SV waves on the seismic response of subway station structure [J]. Engineering Mechanics, 2014, 31(9): 81 − 88, 103. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.03.0278
[34]	FEMA P-58-1, Seismic performance assessment of buildings volume 1-methodology, second edition [S]. Washington, DC: Federal Emergency Management Agency, 2018.
[35]	陈笑宇, 王东升, 付建宇, 等. 近断层地震动脉冲特性研究综述[J]. 工程力学, 2021, 38(8): 1 − 14, 54. doi: 10.6052/j.issn.1000-4750.2020.08.0582 CHEN Xiaoyu, WANG Dongsheng, FU Jianyu, et al. State-of-the-art review on pulse characteristics of near-fault ground motions [J]. Engineering Mechanics, 2021, 38(8): 1 − 14, 54. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.08.0582
[36]	李刚, 程耿东. 基于性能的结构抗震设计: 理论、方法与应用[M]. 北京: 科学出版社, 2004: 1 − 150. LI Gang, CHENG Gengdong. Performance based seismic design: Theory, method and application [M]. Beijing: Science Press, 2004: 1 − 150. (in Chinese)
[37]	杜修力, 蒋家卫, 许紫刚, 等. 浅埋矩形框架地铁车站结构抗震性能指标标定研究[J]. 土木工程学报, 2019, 52(10): 111 − 119, 128. doi: 10.15951/j.tmgcxb.2019.10.009 DU Xiuli, JIANG Jiawei, XU Zigang, et al. Study on quantification of seismic performance index for rectangular frame subway station structure [J]. China Civil Engineering Journal, 2019, 52(10): 111 − 119, 128. (in Chinese) doi: 10.15951/j.tmgcxb.2019.10.009
[38]	刘晶波, 刘祥庆, 李彬. 地下结构抗震分析与设计的Pushover分析方法[J]. 土木工程学报, 2008, 41(4): 73 − 80. LIU Jingbo, LIU Xiangqing, LI bin. A Pushover analysis method for seismic analysis and design of underground structures [J]. China Civil Engineering Journal, 2008, 41(4): 73 − 80. (in Chinese)
[39]	ARGYROUDIS S A, PITILAKIS K D. Seismic fragility curves of shallow tunnels in alluvial deposits [J]. Soil Dynamics and Earthquake Engineering, 2012, 35: 1 − 12. doi: 10.1016/j.soildyn.2011.11.004
[40]	QIU W G, HUANG G, ZHOU H C, et al. Seismic vulnerability analysis of rock mountain tunnel [J]. International Journal of Geomechanics, 2018, 18(3): 04018002. doi: 10.1061/(ASCE)GM.1943-5622.0001080
[41]	于京池, 金爱云, 潘坚文, 等. 基于GA-BP神经网络的拱坝地震易损性分析[J]. 清华大学学报(自然科学版), 2022, 62(8): 1321 − 1329. doi: 10.16511/j.cnki.qhdxxb.2022.25.028 YU Jingchi, JIN Aiyun, PAN Jianwen, et al. GA-BP artificial neural networks for predicting the seismic response of arch dams [J]. Journal of Tsinghua University (Science and Technology), 2022, 62(8): 1321 − 1329. (in Chinese) doi: 10.16511/j.cnki.qhdxxb.2022.25.028
[42]	张业勤. 基于拟静力法的盾构隧道横向地震易损性分析[D]. 武汉: 华中科技大学, 2019. ZHANG Yeqin. Transverse seismic vulnerability analysis of shield tunnel based on pseudo-static method [D]. Wuhan: Huazhong University of Science and Technology, 2019. (in Chinese)

施引文献(11)

期刊类型引用(3)

1.	刘震，吕均琳，马兴亮. 基于ICEEMDAN的近断层地震动识别方法改进. 工程科学与技术. 2024(02): 217-227 . 百度学术
2.	王志岗，陶连金，石城，史明，刘建功. 逆断层错动作用下双仓管廊结构力学特性和抗断设计研究. 土木工程学报. 2024(07): 37-50 . 百度学术
3.	马鹏飞，李东彪，陈新. 因上覆交通荷载引起的既有地下管廊结构变形响应. 北京交通大学学报. 2024(06): 51-67 . 百度学术