STUDY ON INFLUENCE OF WINDWARD ANGLE ON FLIGHT AERODYNAMIC PERFORMANCE OF SKI JUMPERS
-
摘要:
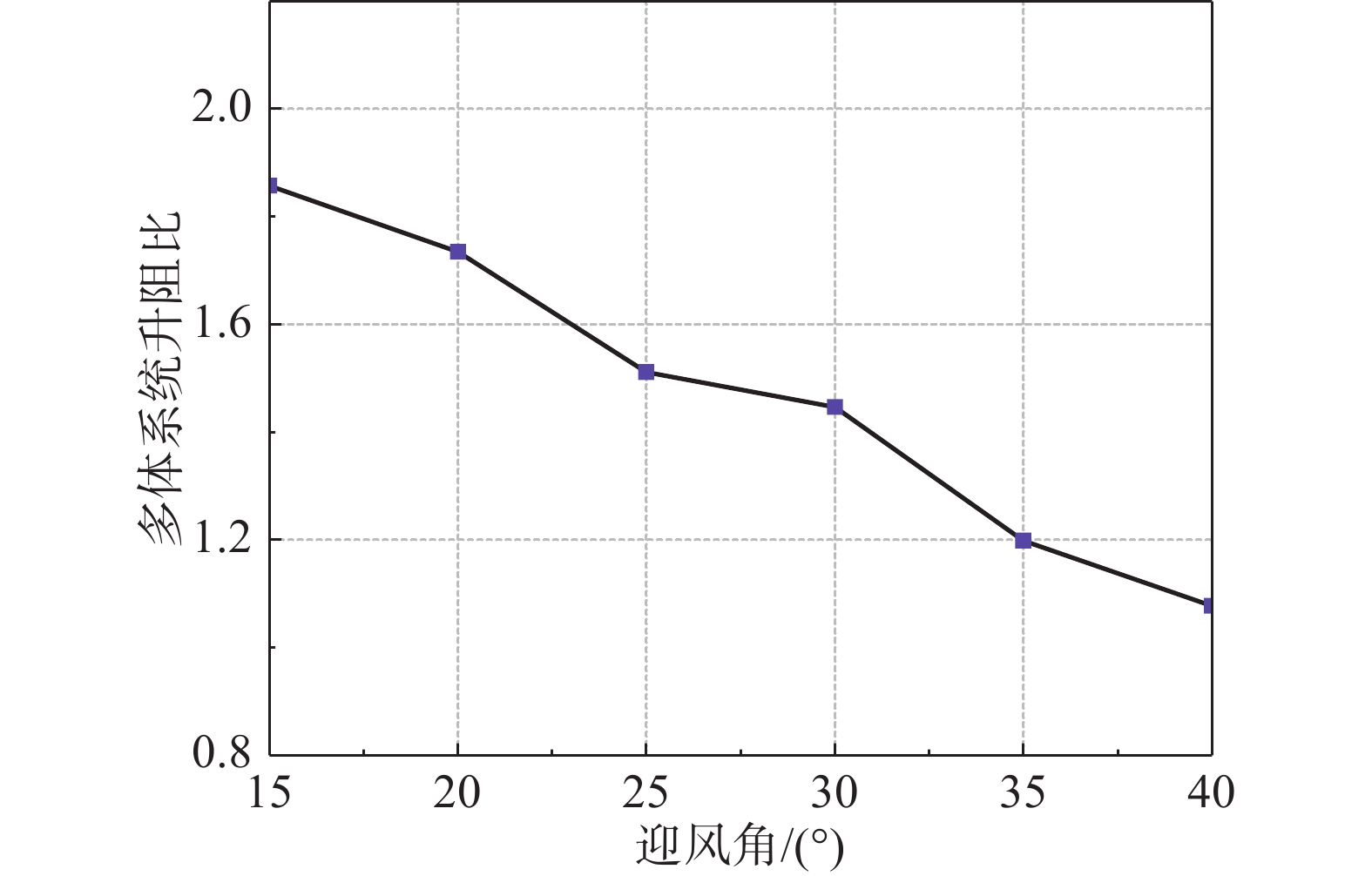
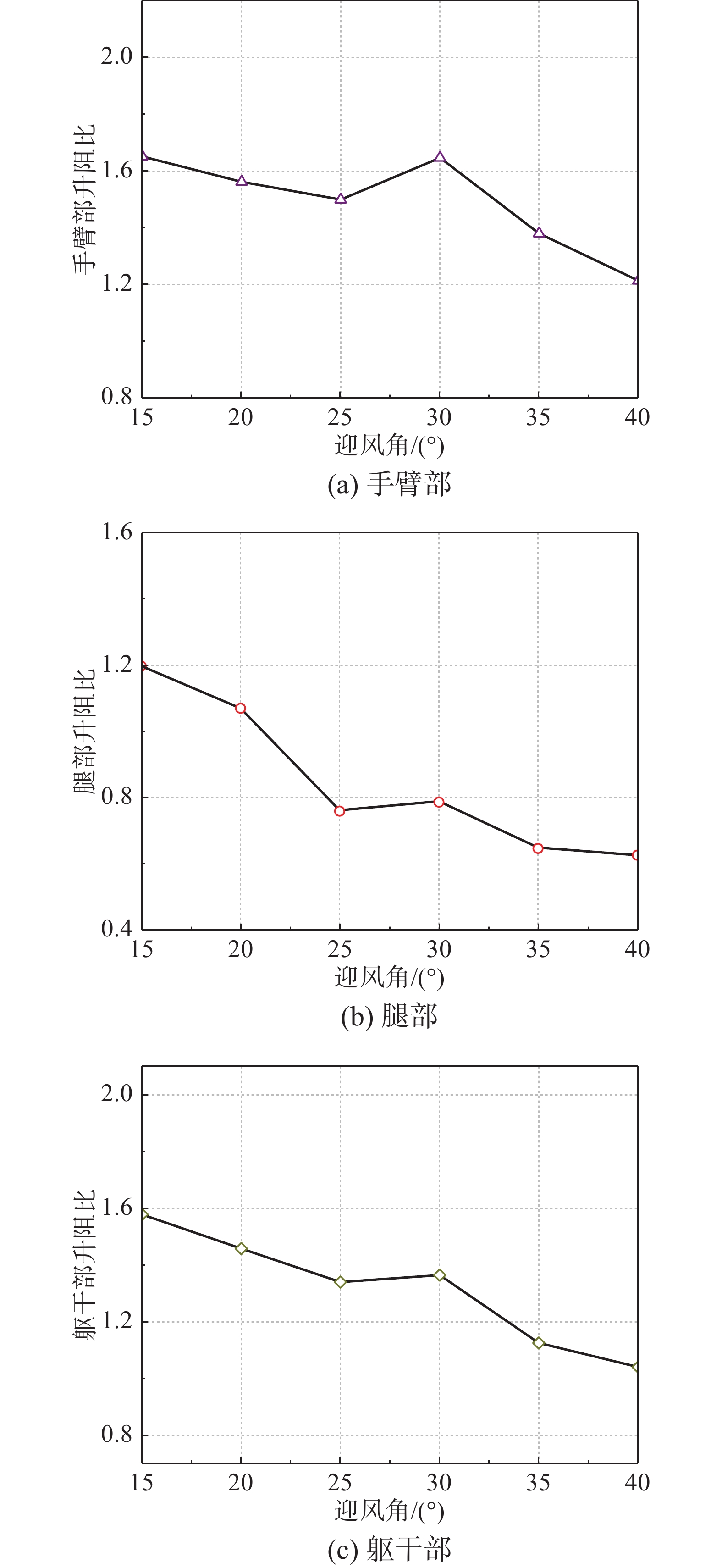
以探究迎风角对跳台滑雪运动员与滑雪板组成的多体系统的飞行气动性能的影响为目的，采用CFD数值模拟方法，在风速为29 m/s情况下，研究了多体系统迎风角为15°、20°、25°、30°、35°、40°六种情况下的气动性能变化情况。并在保证跳台滑雪运动员姿态以及飞行速度不变的情况下，以多体系统的升阻比作为衡量标准，对迎风角对多体系统气动性能的影响情况进行了评估。研究得出：多体系统升阻比随迎风角的增大呈递减趋势，且不同迎风角之间多体系统升阻比差异较大。在多体系统迎风角取为15°时，整个多体系统的升阻比取得最大值，有利于运动员取得良好的气动性能。此外，迎风角对跳台滑雪运动员气动性能影响的研究可为运动员比赛技巧相关的训练提供一定的指导作用。
Abstract:In order to explore the influence of windward angle on the aerodynamic performance of ski jumpers, the CFD (computational fluid dynamics) numerical simulation method was used to study the aerodynamic performance changes of a multibody system under the condition of wind speed of 29 m/s in six situations: windward angle of 15°, 20°, 25°, 30° 35° 40°. It is concluded that: under the condition of ensuring that the attitude and flight speed of ski jumpers are fixed, the lift-to-drag ratio of the entire multi-body system increases first and then decreases with the increase of the windward angle, and the lift-to-drag ratio of the entire multi-body system varies greatly between different wind attack angles. At an angle of attack of 15°, the aerodynamic performance of the entire multibody system is optimal, which can provide some kind of guidance for ski jumpers' training.
-
我国古建筑沿袭着“构木成架”的做法，形成了独树一帜的结构体系。古建筑中的木构架不使用一钉一铆，构件之间采用特殊的榫卯连接方式相互搭接而成，这种榫卯连接方式具有刚柔并济的特点，为典型的半刚性连接。震害调查表明古建筑木结构中的榫卯节点属于弱连接，地震中往往先于梁柱等构件发生破坏，是加固保护的关键部位[1]。因此，有必要对古建筑木结构榫卯节点连接的力学性能进行研究，并提出合理的预防性修缮加固方法。
目前，国内外学者主要通过试验研究、数值模拟及理论分析等方法研究古建筑木结构榫卯节点的力学特征。薛建阳等[2]对通榫节点的柱架模型进行了低周反复荷载试验和有限元数值模拟，模拟结果与试验结果吻合较好；Xue等[3]采用拟静力试验研究了松动对通榫节点和燕尾榫节点抗震性能的影响，研究表明松动节点的承载力、刚度和耗能能力均显著低于完好节点。谢启芳等[4-5]推导了燕尾榫节点弯矩-转角理论计算公式并与试验结果进行了对比，研究表明理论分析结果与试验结果吻合较好；潘毅等[6]建立了木结构直榫节点的M-θ力学模型和相应的实现算法，给出了简化计算公式，并通过试验数据验证该力学模型的合理性；Nakagawa和Ohta[7]研究发现，榫卯节点的刚度是影响整体结构动力特性的关键因素，增加节点刚度会显著提高结构在地震作用下的动力响应，且榫卯节点自身大转动、大变形导致的节点承载力降低是古建筑木结构发生倒塌的主要原因；Li等[8]研究了榫卯损伤对单向直榫木框架抗震性能的影响，研究表明随着损伤程度的增加，木框架的滞回曲线峰值逐渐减小，抗震性能下降。
在榫卯节点抗震加固方面，周乾等[9]分别采用钢构件、马口铁和碳纤维布对榫卯节点进行加固试验，对比分析了不同方法加固榫卯节点的抗震性能；周长东等[10]采用内嵌钢筋外包CFRP布复合加固方法对古建木柱进行了轴心受压试验，试验结果表明复合加固方法能够提高木柱的受压承载力并改善木柱的延性；薛建阳等[11]对采用碳纤维布和扁钢加固节点的木构架进行拟静力试验，试验表明加固后的木构架耗能明显。采用常规的加固方式在提高榫卯节点和木柱的承载能力方面表现良好，但是都没有自复位效果，而形状记忆合金(SMA)是一种变形后可恢复的特殊材料，相对于一般常见的金属材料，SMA具有形状记忆效应和超弹性。Xie等[12-13]采用SMA材料对古建筑榫卯节点进行加固，研究了加固节点的滞回性能，研究结果表明采用SMA加固节点的耗能能力明显提高，SMA用于加固榫卯节点具有良好效果。胡淑军等[14]对5个不带SMA的支撑和6个自复位SMA支撑进行了拟静力试验，试验结果表明自复位SMA支撑具有良好的承载能力和自复位能力；李灿军等[15]建立了摩擦耗能型SMA杆自复位梁柱节点的有限元模型，模型试验结果表明随着SMA杆直径的增大，节点抗弯能力和自复位性能均显著提高，SMA可以用于古建筑木结构的加固保护。
为了在不显著增大榫卯节点抗弯刚度的前提下，较大程度地提高其承载能力和自复位性能，本文提出一种新型SMA丝加固装置并对直榫节点进行预防性加固。通过对5个加固直榫节点及1个未加固节点进行低周反复荷载试验，研究了加固节点的抗震性能，同时提出了加固节点的抗弯承载力计算方法。研究成果可为古建筑木结构的预防性加固保护提供参考。
1 试验概况
1.1 试件设计和制作
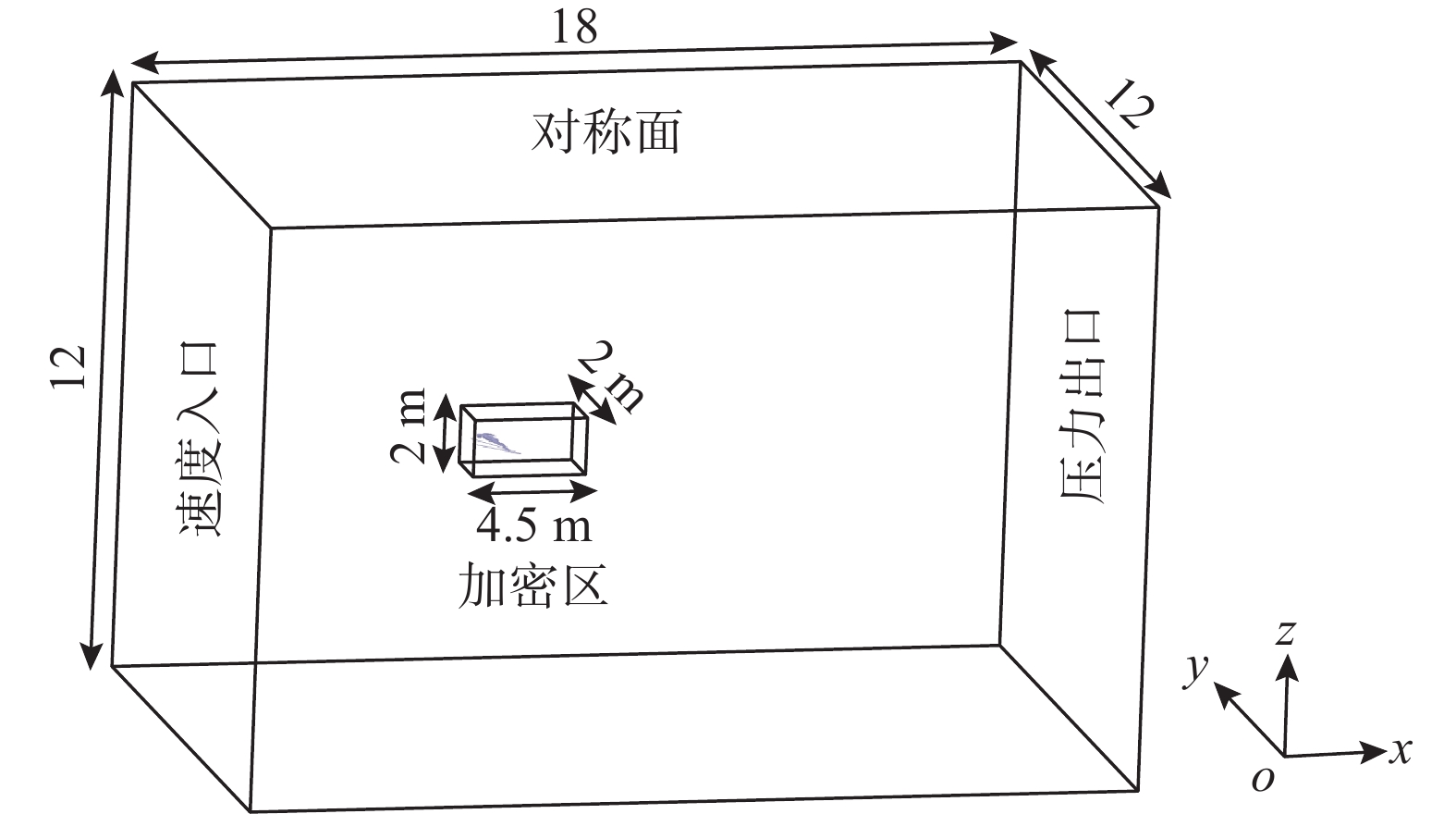
参照宋代《营造法式》[16]中八等材的尺寸要求，采用樟子松作为模型原材料，制作了6个直榫节点模型，试件编号分别为STJ-1~STJ-6，试验模型尺寸如图1所示。
设计了一种新型SMA丝加固装置对直榫节点进行加固，加固示意图见图2，SMA丝一端绕过导杆并穿过空心螺杆，端部通过夹具夹紧并施加预拉力；SMA丝另一端缠绕在带孔的钢杆上，固定在半圆形扁钢箍上，SMA丝梁柱端连接件如图3所示，加固节点试验图如图4所示，试件设计参数如表1所示。
表 1 试件设计参数Table 1. Design parameters of specimens试件编号 SMA丝 直径/mm 根数 预拉应变/(%) 长度/mm STJ-1 未加固 STJ-2 1.5 12 3 1500 STJ-3 16 3 STJ-4 20 0 STJ-5 20 1 STJ-6 20 3 1.2 加载方案
试验加载过程中，木柱水平放置，木枋竖向放置，木柱左、右两端固定不动，并用压梁压紧木柱。木柱一端采用千斤顶施加轴向荷载30 kN，在木枋上距木柱节点1100 mm的位置进行水平低周往复加载，加载示意图见图5。
采用位移控制方法进行加载，加载速率为5 mm/min，预估直榫节点的极限转角为0.1 rad，即极限控制位移的预估值Δu=110 mm，采用极限控制位移的10%、20%、30%、40%、50%各进行1次循环加载，之后采用极限控制位移的60%、80%、100%、120%各进行3次循环加载，加载完成后复位并结束试验，加载制度如图6所示，图中Δ表示加载位置的水平位移。
1.3 测量方案
采用位移计测量榫头的拔出量，采用倾角仪测量节点的转角。
1.3.1 榫头拔出量测量
在榫头抱肩处左、右两侧各设置2个位移计，记为W1~W4，用来测量榫头的拔出量，如图7所示。
1.3.2 节点转角测量
在靠近梁柱节点的枋端设置一个倾角仪，用来测量梁柱之间的相对转角即节点转角，如图8所示。
1.4 木材及SMA丝力学性能
采用樟子松制作榫卯节点，木材强度试验按照《木结构试验方法标准》(GB/T 50329−2012)进行测试，通过材性试验测得其力学性能参数，各项数据统计如表2所示。
表 2 木材力学性能Table 2. Mechanical properties of wood顺纹抗拉
强度/MPa顺纹抗压
强度/MPa顺纹抗剪
强度/MPa横纹抗压
强度/MPa弹性
模量/MPa径向 弦向 顺纹 横纹
径向横纹
弦向83.17 19.23 5.19 2.04 2.89 8772.92 147.02 468.02 对试验采用的同一批次的加固材料SMA丝进行材性试验，试验程序严格按照《金属材料拉伸试验 第1部分：室温试验方法》(GB/T 228.1−2010)的要求，测得其应力-应变关系，如图9所示。
由材性试验测得SMA丝的材料性能如表3所示。
表 3 SMA丝材料性能Table 3. Material properties of SMA stings力学参数 E/MPa fy/MPa fu/MPa fu/fy δ/(%) 试验值 69 000 502 1114 2.22 44.50 注：E为SMA丝的弹性模量；fy和fu分别为SMA丝的屈服抗拉强度和极限抗拉强度；δ为SMA丝的极限伸长率。 2 试验现象
2.1 未加固模型
未加固试件和加固试件在节点处的破坏形态基本相同，破坏主要产生在榫头和卯口的接合部位，木柱和木枋的整体形态基本未破坏。加载前期，节点处榫头和卯口没有产生明显变形；当节点转角加载到0.02 rad，榫头和卯口开始产生明显的挤压变形，变形主要为弹性变形，加载时出现轻微的“吱吱”声，东侧榫头开始微小拔出，榫头拔出量为1 mm，西侧无拔榫；当节点转角加载到0.06 rad，节点处榫头和卯口产生塑性的挤压变形，榫头被压裂，枋端出现竖向裂缝；持续加载，节点转角继续增大，前述各破坏形态相继发展；当节点转角加载到0.12 rad，节点变形较大，不利于继续加载而结束试验，此时榫头最大拔出量约为23 mm。试验现象和破坏状态如图10所示。
2.2 加固模型
加固节点试件STJ-2~STJ-6加载前期试验现象同STJ-1试件相似，其榫头拔出量明显比未加固节点小，当节点转角加载到0.02 rad，合金丝开始轻微拨动，并伴随微小的“吱吱声”，两侧无拔榫；当节点转角加载到0.06 rad，合金丝连续拨动，出现连续沉闷的“咚咚声”，榫肩木纤维褶皱，榫头拔出量为9 mm；当节点转角持续加载到0.12 rad，由于合金丝根数较少，试件STJ-2东侧出现几条合金丝拉断，最后由于节点转角较大不利于继续加载而结束试验；各加固试件枋自榫头左、右两端向上一定长度内均留下2条明显的竖向劈裂裂缝，试验后拔出榫头，发现试件STJ-4榫头出现劈裂；各加固试件卯口处木纤维剥落并产生明显的压痕。试验现象和破坏状态如图11所示。
3 试验结果及其分析
3.1 M-θ滞回曲线
直榫节点模型的M-θ滞回曲线如图12所示，其中M和θ可以通过下式计算：
M=F×h (1) θ=Δ/h (2) 式中：F/kN为加载位置水平荷载；h/m为加载位置至柱上表面的高度；Δ/m为加载位置的水平位移。
图12中STJ-1(未加固)表示试件STJ-1没有采用SMA丝进行加固，STJ-2(12，3%)表示试件STJ-2所采用的SMA丝的根数为12根，SMA丝的预拉应变为3%，其余图注含义类推。
1) 整体上，节点STJ-1的滞回曲线呈反“Z”形，具有明显的捏缩效应；加载前期，曲线出现滑移段，并随着节点转角的增大而延长，这是因为榫头和卯口接合部位存在初始缝隙，且节点在每级位移幅值加载完成后均产生新的缝隙，此时节点弯矩主要由榫头和卯口接触面间的摩擦力来承担；加固节点STJ-2~STJ-6的滞回曲线呈反“S”形，节点转角零点处，曲线存在一定的斜率，这是因为加载前期的节点弯矩主要由榫头和卯口接触面间的摩擦力以及SMA丝共同来承担，SMA丝承担的弯矩和节点转角具有正相关性，导致滞回曲线在零点处存在一定的斜率。
2) 对于未加固节点STJ-1：加载前期，曲线斜率几乎为0，主要是因为节点处榫头和卯口间存在初始缝隙；当节点转角加载到0.02 rad时，曲线明显开始快速上升，这是因为榫头和卯口表面接触并产生挤压变形，挤压接触面积相应地增大，此时主要为弹性变形；节点转角持续加载到0.06 rad后，曲线上升速率相对减缓，这是因为榫头和卯口挤压产生塑性变形同时榫头部分拔出造成挤压接触面积减小，节点刚度随之降低；卸载时，曲线下降速率较快，此时弹性变形恢复，而残余变形不可恢复且所占比例较大。
3) 与未加固节点STJ-1进行对比，加固节点峰值承载力均比未加固节点的大，滞回环更加饱满；SMA丝数量越多，预拉应变越大，其峰值承载力越大；节点STJ-6正向加载时，节点弯矩上升速率较快，当节点转角加载到0.03 rad后，节点弯矩上升趋势减缓，这是因为节点STJ-6榫头东侧存在初始裂缝，加载过程中，榫头东侧上端由于挤压产生横向裂缝。卸载时，加固节点的残余变形较未加固节点STJ-1小，这是因为卸载过程中SMA丝可以为节点提供部分恢复力，减小了其残余变形。
4) 对比分析未加固节点STJ-1和加固节点STJ-4、STJ-6的滞回曲线(即图12中的红色加粗虚线)，可以看出，未加固节点STJ-1的滞回曲线存在较长的滑移段，加固节点STJ-4的SMA丝预拉应变为0时，其正向加载阶段也存在滑移段，这是因为榫头和卯口接合部位存在初始缝隙，此时节点弯矩主要由榫头和卯口接触面间的摩擦力来提供；而加固节点STJ-6的SMA丝预拉应变为3%时，其正向加载阶段无滑移段，正向卸载阶段滑移段不明显，这是因为SMA丝预拉应变的存在，可以为节点提供部分恢复力，表现出明显的自复位性能。
3.2 骨架曲线
图13为节点模型的骨架曲线，可以看出：
1) 所有节点的骨架曲线具有相似的变化趋势：曲线主要经历了弹性阶段和屈服阶段；加载前期，曲线斜率较大，这是因为榫头和卯口表面开始接触挤压，且挤压接触面积随之增大，挤压变形主要为弹性变形；当节点转角加载到0.06 rad后，骨架曲线进入屈服阶段，节点弯矩增长减缓，这是因为榫头和卯口表面因接触面积较大而发生挤压破坏，此时变形主要为塑性变形；骨架曲线最后趋于平缓，没有出现下降段，表明节点在较大变形的情况下仍然存在较强的抗弯能力。
2) 当SMA丝预拉应变相同时，正向加载试件时，加固节点STJ-6的最大抗弯承载力是未加固节点STJ-1的1.49倍，节点STJ-3的最大抗弯承载力是节点STJ-1的1.19倍，节点STJ-2的最大抗弯承载力是节点STJ-1的0.89倍，表明随着SMA丝根数的增加，节点的最大抗弯承载力不断增大，而加固节点STJ-2的最大抗弯承载力略低于未加固节点，这是因为试件STJ-2出现几条合金丝拉断造成的；反向加载试件时，节点STJ-6和节点STJ-3的最大抗弯承载力基本相同，这是因为两者的最终榫头拔出量基本相同。
3) 当SMA丝根数相同时，正向加载试件时，加固节点STJ-6的最大抗弯承载力是未加固节点STJ-1的1.49倍，节点STJ-5的最大抗弯承载力是节点STJ-1的1.31倍，节点STJ-4的最大抗弯承载力是节点STJ-1的1.25倍，表明随着SMA丝预拉应变的增大，节点的最大抗弯承载力也不断增大。加固节点的抗弯承载力相比于未加固节点STJ-1均有不同程度的提高，且SMA丝根数越多，预拉应变越大，节点的抗弯承载力提高的程度越大。
3.3 强度退化
在水平拟静力加载试验中，相同的位移幅值下进行了3个加载循环，随着加载循环次数的增加，作用在节点上的水平荷载逐渐减小。强度退化因子可计算如下式：
λi=Pi,3Pi,1 (3) 式中：λi为第i个位移幅值的强度退化因子；Pi,1为第i个位移幅值中第1个周期的峰值荷载；Pi,3为第i个位移幅值中第3个周期的峰值荷载。
通过式(3)计算出各节点模型的强度退化因子λi的变化规律如图14所示，可以得到：
1) 节点转角未加载到0.06 rad 时，各节点模型的强度退化因子均随着转角的增大而几乎不变，此时节点的抗弯能力主要是由榫卯接触面间的摩擦产生的塑性变形来提供。
2) 当节点转角超过0.06 rad时，未加固节点STJ-1的强度退化因子快速减小，而加固节点的强度退化因子均在0.95上下波动，这说明加固节点的强度退化不严重，表明SMA丝可以在节点转角较大时，仍能持续为节点提供抗弯承载力，加固的效果较为明显。
3.4 刚度退化
随着加载循环次数和位移幅值的增大而刚度逐渐减小的现象称为刚度退化，在水平反复荷载作用下，刚度可以采用各级加载位移下滞回曲线的割线刚度来表示，计算公式如下：
Ki=|+Mi|+|−Mi||+θi|+|−θi| (4) 式中：Ki为第i级加载位移作用下的割线刚度；Mi为第i级加载位移作用下的峰值点弯矩；θi为Mi对应的节点转角。
通过式(4)计算出各节点模型转动刚度如图15所示，可以得到：
1) 各试件节点的转动刚度具有相似的变化规律：转动刚度均随着转角的增大而减小；刚度退化曲线可分为快速下降阶段、缓慢下降阶段和稳定阶段 3个阶段，加载前期，节点转动刚度退化速率较快，这是因为榫卯节点之间存在初始缝隙，节点滑移导致其刚度快速退化，当节点转角持续加载到0.06 rad后，转动刚度下降减缓并最终趋于稳定。
2) SMA丝可以一定程度地提高节点的初始刚度，但随着节点转角的增加，加固后的节点刚度退化更为严重。
3) SMA丝预拉应变相同时，加固节点STJ-6的初始转动刚度是未加固节点STJ-1的2.24倍，节点STJ-3的初始转动刚度是节点STJ-1的1.88倍，节点STJ-2的初始转动刚度是节点STJ-1的1.45倍，表明SMA丝根数越多，节点的初始刚度提高程度就越大。
4) SMA丝根数相同时，SMA丝预拉应变越大，对节点的初始刚度提高程度也越大；当节点转角加载到0.12 rad，加固节点STJ-6的转动刚度是未加固节点STJ-1的1.50倍，节点STJ-5的转动刚度是节点STJ-1的1.40倍，节点STJ-4的转动刚度是节点STJ-1的1.28倍，加固后的节点刚度依旧大于未加固节点的刚度，加固的效果较为显著。
为了研究不同加固方法对节点初始刚度的提升程度，将现有加固方式进行了对比分析，如表4所示。由表4可以看出，采用SMA丝加固时，节点的初始刚度不显著提高，该加固方法对直榫节点的初始刚度影响较小，不显著改变结构的结构性能，有效避免了刚度增加导致结构动力响应的增大。而常规加固方式在提高节点的承载力方面表现良好，但是都没有自复位效果。
表 4 不同加固方法对节点性能的提升倍数Table 4. Increment magnification of joint performances considering different methods3.5 耗能性能
通常用等效黏滞阻尼系数he来表示节点的耗能能力，he的计算方法示意图如图16所示，计算公式如下：
he=12πS(\wideparenABD+\wideparenCBD)S△DEO+S△BFO (5) 式中：he为等效黏滞阻尼系数；S(ABD+CBD)为滞回环的面积，即图16中阴影部分的面积；S△DEO为△DEO的面积；S△BFO为△BFO的面积。
![]()
图 16 等效黏滞阻尼系数计算图Figure 16. Calculation diagram of equivalent viscous damping coefficient通过式(5)计算出节点模型的等效黏滞阻尼系数he的变化规律如图17所示，由图可知：
1) 随着节点转角的不断增大，未加固节点STJ-1的耗能能力逐渐减小，这是因为加载前期，直榫节点耗散的能量主要由榫卯间的摩擦力来提供，此时节点弯矩较小，耗能能力较强；继续加载，节点处开始产生挤压变形，节点弯矩相继增大，节点耗能能力主要由挤压变形中的塑性变形来提供，而塑性变形增加的速率随着节点转角的增大而减小，故节点的耗能能力逐渐减小。
2) 随着节点转角的不断增大，加固节点STJ-2~STJ-6的耗能能力先增大后减小，分析原因为：加固节点的耗能能力是由直榫节点和SMA丝共同承担，而SMA丝耗散的能量远小于直榫节点耗散的能量，SMA丝耗散的这部分能量可以忽略不计；加载前期，节点弯矩较小，SMA丝对节点弯矩的提升效果显著，在耗散能量一定的情况下，耗能能力与节点弯矩呈反比，故加载前期加固节点的耗能能力较差；随着节点转角的持续增大，SMA丝对节点弯矩的提升效果逐渐减弱，加固节点的耗能能力与未加固节点的耗能能力越来越接近，故加固节点的耗能能力呈先增大后减小的规律。除STJ-6之外，在相同的转角下，加固节点的等效黏滞阻尼系数数值大小较为接近，表明SMA丝的根数和预拉应变的大小对节点的耗能能力影响不大。
3.6 自复位能力
在每个加载循环中，滞回曲线和
X轴交点的横坐标的绝对值反映了节点的自复位能力。图18为STJ-6的最后一个加载循环的滞回曲线，图中滞回曲线和X轴横坐标的交点为B和C，滞回曲线正负向最大转动对应的点为A和D， D+r 和D−r 分别为正向和负向残余变形，通过式(6)和式(7)计算所得，为了减小试验偶然误差，计算了节点的相对残余变形Dr，计算公式见式(8)。D+r=XC/XD (6) D−r=XB/XA (7) Dr=∑(D+r+D−r)2 (8) 通过计算得到各个试件的相对残余变形Dr和转角θ的关系见图19，可以得到：
1) 由图19可以看出，在相同的转角下，随着SMA丝根数的增加，相对残余变形减小，自复位能力增强；同样地，随着SMA丝预拉应变的增加，相对残余变形也减小，自复位能力也提高。
2) 未加固节点STJ-1在加载前期榫卯接触紧密，相对残余变形较小，节点具有良好的自复位能力。当节点转角未加载到0.05 rad，摩擦接触面积减小，相对残余变形增大，自复位能力开始下降；当节点转角大于0.05 rad和小于0.08 rad时，直榫节点出现明显的滑移，相对残余变形显著减小，自复位能力提高；当节点转角加载超过0.08 rad时，直榫节点出现较大的变形，相对残余变形略微增大。
3) 各加固节点的相对残余变形明显小于未加固节点。当节点转角未加载到0.02 rad时，加固节点的相对残余变形略微增加，这是因为直榫节点木构件之间的摩擦接触面积减小，从而减小了节点的自复位能力；当节点转角超过0.02 rad时，SMA丝出现较大的塑性拉伸变形，此时节点的自复位能力主要由SMA丝来提供，节点的相对残余变形明显减小，自复位能力增强。
3.7 节点转动能力
参照《古建筑木结构维护与加固技术标准》(GB 50165−2020)可以得到：木结构的层间位移角限值为1/30，由于其变形主要是由直榫节点转动引起的，可大概认为直榫节点转角的限值为1/30。
由图13可以看出：当节点转角加载到0.12 rad时(约1/8)，节点弯矩仍然没有出现下降，且未能达到极限弯矩，此时由于节点转角较大不利于继续加载而结束试验。节点的最大转角大于规范规定的转角限值1/30，表明加固直榫节点的转动变形能力较好。
4 承载力计算
为了评估新型加固节点的承载力，提出了SMA丝加固直榫节点的抗弯承载力计算方法，根据实际测得的SMA丝的应力-应变关系曲线，同时参照Shaw等[19]和Chang等[20]研究中SMA丝的简化本构关系，作出如下假设：1)假设形变均匀产生；2) SMA丝始终处于充分的预张拉状态，避免SMA丝变为马氏体；3)奥氏体和马氏体相变期间的应力保持不变；4)由于材料试验采用了准静态加载方案，认为相变速率要比加载速率快得多。由此得到SMA丝的应力-应变关系简化模型，如图20所示。通过拉伸加卸载试验结果，得到SMA丝的力学性能参数的平均值和变异系数，如表5所示。
表 5 SMA丝力学性能参数Table 5. Mechanical parameters of SMA strings参数 σb/MPa σc/MPa E1/GPa E2/GPa εa/(%) εb/(%) εc/(%) εd/(%) 平均值 510.0 218.0 69.0 29.0 0.7 0.9 7.4 8.4 变异系数/(%) 9.3 7.9 26.6 10.0 17.7 22.6 4.1 2.0 注：σb和σc分别为SMA丝从奥氏体到马氏体和从马氏体到奥氏体的相变应力；E1和E2分别为奥氏体弹性模量和马氏体弹性模量；εa、εb、εc和εd为应变特征值。 直榫节点的连接构造模型见图4所示，由直榫节点提供的弯矩[21]计算公式见式(9)。
M1=M0+kθ[1+(θ/θ0)n]1/n (9) θ0=Mu−M0k (10) 式中：M0为初始弯矩；k为初始刚度；θ0为节点的相对转动角度；Mu为极限弯矩；n为形状系数。
对于理想节点，当转动角度为0时，初始弯矩为0，因此，式(9)中考虑M0=0，得到直榫节点提供的弯矩计算公式见下式：
M1=kθ[1+(θ/θ0)n]1/n (11) 如图21所示，当SMA丝加固节点逆时针旋转，转动角度θ较小时，左右合金丝分别存在拉力P1和P2。根据图20所示的SMA丝应力-应变简化关系，计算出SMA丝产生的拉力见下式：
P1={E1ε1A,0⩽ (12) {P_{\rm{2}}} = \left\{ {\begin{array}{*{20}{l}} {{E_1}{\varepsilon _2}A},&{0 \leqslant {\varepsilon _2} \leqslant {\varepsilon _{\rm{b}}}}\\ {{\sigma _{\rm{b}}}A},&{{\varepsilon _{\rm{b}}} < {\varepsilon _2} \leqslant {\varepsilon _{\rm{d}}}} \end{array}} \right.\qquad\qquad\qquad (13) 式中：
{\varepsilon _1} 为SMA丝左侧的拉应变；{\varepsilon _2} 为SMA丝右侧的拉应变；A为SMA丝一侧的面积。SMA丝和木枋的初始夹角为π/4，当转动角度为θ时，左、右两侧SMA丝的应变增量
\Delta {\varepsilon _1} 和\Delta {\varepsilon _2} 分别用式(14)和式(15)表示：\Delta {\varepsilon _1} = \dfrac{{{L_{{{AE}}}'} - {L_{{{AE}}}}}}{{{L_{{{AE}}}}}} = \dfrac{{2L{\rm{cos}}\left( {\dfrac{{\rm{\pi }}}{4} + \dfrac{\theta }{2}} \right) - \sqrt 2 L}}{{\sqrt 2 L}} (14) \Delta {\varepsilon _2} = \dfrac{{{L_{{{DF}}}'} - {L_{{{DF}}}}}}{{{L_{{{DF}}}}}} = \dfrac{{2L{\rm{cos}}\left( {\dfrac{{\rm{\pi }}}{4} - \dfrac{\theta }{2}} \right) - \sqrt 2 L}}{{\sqrt 2 L}} (15) 式中，L为SMA丝的长度。
式(12)和式(13)中的拉应变
{\varepsilon _1} 和{\varepsilon _2} 通过下式计算得到：{\varepsilon _1} = \Delta {\varepsilon _1} + \alpha = \sqrt 2 {\rm{cos}}\left( {\frac{{\rm{\pi }}}{4} + \frac{\theta }{2}} \right) - 1 + \alpha (16) {\varepsilon _2} = \Delta {\varepsilon _{\rm{2}}} + \alpha = \sqrt 2 {\rm{cos}}\left( {\frac{{\rm{\pi }}}{4} - \frac{\theta }{2}} \right) - 1 + \alpha (17) 式中，α为SMA丝的预拉应变。
在图21中，假设转动中心在点G处，SMA丝提供的弯矩计算式如下：
\begin{split} {M_2} = & {P_2}\left( {s + \frac{t}{2}} \right){\rm{sin}}\left( {\frac{{\rm{\pi }}}{4} - \frac{\theta }{2}} \right) -\\& {P_1}\left( {s + \frac{t}{2}} \right){\rm{sin}}\left( {\frac{{\rm{\pi }}}{4} + \frac{\theta }{2}} \right) \end{split} (18) 综上所述，通过代入方程式，可得到加固节点弯矩M和转角θ的表达式为式(18)，故由直榫节点和SMA丝共同提供的总弯矩见下式：
M = {M_1} + {M_2} (19) 当SMA丝出现受拉拔断和受压屈曲时，即FD段SMA丝受拉拔断，AE段SMA丝受压屈曲，此时左、右合金丝存在的拉力P1和P2均为0，由SMA丝提供的弯矩值M2=0，节点的总弯矩由直榫节点所提供，即M=M1，式(19)依旧能满足需求。
通过式(19)计算出6个试件的弯矩值，选取试件STJ-1、STJ-4、STJ-6的计算总弯矩和试验总弯矩对比如图22所示。由图22可以看出，采用式(19)计算出节点的弯矩值和试验得到的弯矩值整体吻合较好，随着节点转角的增大，两者的误差略微增大。进而统计了6个试件的理论计算最大弯矩值与试验测得的最大弯矩值见表6，可以得到，各个试件的理论计算弯矩值和试验测得的弯矩值之间的相对误差值均在10%左右，表明所建立的承载力计算方法较为合理。
表 6 计算值与试验值对比Table 6. Comparison of calculated and experimental values试件编号 STJ-1 STJ-2 STJ-3 STJ-4 STJ-5 STJ-6 形状系数n 0.75 0.68 0.63 0.58 0.56 0.65 计算最大弯矩值M/(kN·m) 20.70 20.89 30.28 27.36 29.84 33.89 试验最大弯矩值M'/(kN·m) 22.16 22.95 32.08 30.66 33.49 35.83 相对误差/(%) 6.59 8.98 5.61 10.76 10.90 5.41 注：试验弯矩值由正、负向最大抗弯承载力取平均值计算所得。 5 结论
通过低周反复荷载试验，研究了SMA丝加固直榫节点的抗震性能，并提出了SMA丝加固直榫节点抗弯承载力计算方法，得到以下主要结论：
(1) 未加固节点的滞回曲线呈反“Z”型，具有明显的捏缩和滑移效应，加固节点的滞回曲线呈反“S”型，滞回环更加饱满，加固节点的滞回环峰值承载力比未加固节点大，并且SMA丝根数越多，SMA丝预拉应变越大，节点的承载力越高。
(2) 各节点的抗弯承载力均随节点转角的增大而增大，并未出现下降段，且逐渐趋于平缓。SMA丝加固后节点的抗弯承载力均不同程度地提升，加固节点最大抗弯承载力是未加固节点的1.49倍；SMA丝根数越多，且预拉应变越大，节点抗弯承载力的提升程度越大。同时SMA丝可以在节点转角较大时，仍能持续为节点提供抗弯承载力。
(3) 各节点的转动刚度均随节点转角的增大而减小，刚度退化速率逐渐减小，并趋于稳定，且加固节点的转动刚度均大于未加固节点，加固节点最大转动刚度是未加固节点的2.24倍。
(4) 随着节点转角的逐渐增大，未加固节点的耗能能力逐渐减小，而加固节点的耗能能力先增大后减小，且SMA丝根数和预拉应变的大小对节点耗能能力影响不大。但在相同的转角下，随着SMA丝根数和预拉应变的增加，相对残余变形均减小，自复位能力增强。
(5) 提出了SMA丝加固直榫节点的抗弯承载力计算方法，计算值和试验值吻合良好，表明该方法可有效预测加固节点的抗弯承载力，为古建筑木结构的预防性加固保护设计提供参考。
-
![]()
图 1 多体系统飞行姿态参数及受力情况
Figure 1. Posture parameters and forces acting on the athlete/skis system during flight
![]()
图 4 多体系统升阻比随迎风角的变化曲线
Figure 4. Aerodynamic characteristics of the systems as a function of angle of attack
![]()
图 5 身体各部位升阻比随迎风角变化曲线
Figure 5. Aerodynamic characteristics of different parts as a function of angle of attack
![]()
图 7 y=0 平面处平均压力云图以及平均速度流线图
Figure 7. Pressure distribution and streamlines on y=0 plane with different angle of attack
![]()
图 8 z=0 平面处平均压力云图以及平均速度流线图
Figure 8. Pressure distribution and streamlines on z=0 plane with different angle of attack
![]()
图 9 不同风攻角下多体系统Q准则涡结构无量纲化速度云图侧视图({{Q}} = 40{{U}}_0^2/{{{L}}^2})
Figure 9. Q-criterion iso-surfaces at {{Q}} = 40{{U}}_0^2/{{{L}}^2} colored by the normalized streamwise velocity of multi-body system at different angle of attack
表 1 运动员姿态参数及计算工况
Table 1 Values of posture parameters and calculation conditions during flight
参数 角度/(°) 滑雪板与速度方向夹角α 25 滑雪板与身体夹角θ 20 上半身弯曲角度β 10 滑雪板夹角λ 27.5 迎风角φ 15/20/25/30/35/40 
下载: 导出CSV
表 2 运动员及滑雪板模型尺寸
Table 2 Geometric dimension of athlete/skis
运动员 滑雪板 身高/m 质量/kg 长度/m 宽度/m 厚度/mm 1.77 61.1 2.58 0.115 10
下载: 导出CSV
表 3 计算方法设置概况
Table 3 Summarization or simulation parameters
输入变量 参数/设置 湍流模型 SST k-ω 压力速度耦合方式 Coupled 空间离散方式 二阶迎风 时间积分方法 二阶迎风 收敛准则 10−5
下载: 导出CSV
表 4 跳台滑雪多体系统气动性能相关研究对比
Table 4 Model validation and comparative results of the ski-jumping athlete
方案 研究方法 风速/(m/s) 迎风角/(°) 滑雪板间夹角/(°) 腿部与滑雪板夹角/(°) 升阻比 廖章文等[13] 数值模拟(k-ε模型、k-ω模型) 28.0 30 18 28 1.66 胡齐等[6] 数值模拟(PANS模型) 29.0 30 28 16 1.97 NØRSTRUD等[14] 数值模拟(k-ε模型、k-ω模型) 25.8 20 20 10 2.42 刘丹等[15] 数值模拟(k-ω模型) 20.0 20 28 20 1.98 GARDAN等[5] 数值模拟(k-ω模型) 29.0 29 38 17 1.91 CHOWDHURY等[16] 风洞试验 27.8 10 30 30 1.48 30.6 10 30 30 1.53 ELFMARK等[17] 现场实测 27.8 − − − 1.47 30.6 − − − 1.53 本文 数值模拟(SST k-ω模型) 29.0 25 28 25 1.51
下载: 导出CSV
-
[1] 刘庆宽, 孙一飞, 张磊杰, 等. 凹痕对斜拉桥斜拉索气动性能影响研究[J]. 工程力学, 2019, 36(增刊): 272 − 277. doi: 10.6052/j.issn.1000-4750.2018.05.S053 LIU Qingkuan, SUN Yifei, ZHANG Leijie, et al. Study on the influence of dent on aerodynamic performance of stay cables of cable-stayed bridge [J]. Engineering Mechanics, 2019, 36(Suppl): 272 − 277. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S053
[2] 王仰雪, 刘庆宽, 靖洪淼, 等. 倾斜栏杆对流线型箱梁涡激振动性能影响的试验研究[J]. 振动与冲击, 2023, 42(6): 232 − 239, 254. WANG Yangxue, LIU Qingkuan, JING Hongmiao, et al. Experimental study on the influence of inclined railings on the vortex-induced vibration performance of a streamlined box girder [J]. Journal of Vibration and Shock, 2023, 42(6): 232 − 239, 254. (in Chinese)
[3] 郑肖楠, 崔会敏, 刘庆宽. 超高层建筑表面风压及行人风环境研究[J]. 工程力学, 2021, 38(增刊): 223 − 227. doi: 10.6052/j.issn.1000-4750.2020.05.S040 ZHENG Xiaonan, CUI Huimin, LIU Qingkuan. Study on surface wind pressure and pedestrian wind environment of super high-rise buildings [J]. Engineering Mechanics, 2021, 38(Suppl): 223 − 227. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.S040
[4] 柴晓兵, 刘庆宽, 郑云飞. 结构干扰对煤棚表面风荷载影响的试验研究[J]. 工程力学, 2023, 40(增刊): 174 − 183. doi: 10.6052/j.issn.1000-4750.2022.06.S029 CHAI Xiaobing, LIU Qingkuan, ZHENG Yunfei. Wind tunnel experiment study on wind load of coal shed structure by interference effect [J]. Engineering Mechanics, 2023, 40(S): 174 − 183. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.06.S029
[5] GARDAN N, SCHNEIDER A, POLIDORI G, et al. Numerical investigation of the early flight phase in ski-jumping [J]. Journal of Biomechanics, 2017, 59: 29 − 34. doi: 10.1016/j.jbiomech.2017.05.013
[6] 胡齐, 刘宇. 运动员姿态对跳台滑雪空中飞行气动特性的影响[J]. 医用生物力学, 2021, 36(3): 407 − 414. HU Qi, LIU Yu. Effects of Athlete’s posture on aerodynamic characteristics during flight in ski jumping [J]. Journal of Medical Biomechanics, 2021, 36(3): 407 − 414. (in Chinese)
[7] SCHWAMEDER H, MÜLLER E, LINDENHOFER E, et al. Kinematic characteristics of the early flight phase in ski-jumping [M]// MÜLLER E, BACHARACH D, KLIKA R, et al. Science and Skiing III. Oxford: Meyer & Meyer Sport, 2005: 381 − 391.
[8] VIRMAVIRTA M, ISOLEHTO J, KOMI P, et al. Characteristics of the early flight phase in the Olympic ski jumping competition [J]. Journal of Biomechanics, 2005, 38(11): 2157 − 2163. doi: 10.1016/j.jbiomech.2004.10.004
[9] MEILE W, REISENBERGER E, MAYER M, et al. Aerodynamics of ski jumping: Experiments and CFD simulations [J]. Experiments in Fluids, 2006, 41(6): 949 − 964. doi: 10.1007/s00348-006-0213-y
[10] JUNG A, STAAT M, MÜLLER W. Flight style optimization in ski jumping on normal, large, and ski flying hills [J]. Journal of Biomechanics, 2014, 47(3): 716 − 722. doi: 10.1016/j.jbiomech.2013.11.021
[11] MÜLLER W, GRÖSCHL W, MÜLLER R, et al. Underweight in ski jumping: The solution of the problem [J]. International Journal of Sports Medicine, 2006, 27(11): 926 − 934. doi: 10.1055/s-2006-923844
[12] 胡齐, 刘宇. 环境风对跳台滑雪空中飞行气动特性的影响[J]. 体育科学, 2020, 40(3): 54 − 63. HU Qi, LIU Yu. Effects of wind on the aerodynamic characteristics during flight in ski jumping [J]. China Sport Science, 2020, 40(3): 54 − 63. (in Chinese)
[13] 廖章文, 周义翔, 于经伦, 等. 基于CFD仿真的跳台滑雪空中飞行姿态优化及其验证研究[J]. 摩擦学学报, 2023, 43(10): 1151 − 1164. LIAO Zhangwen, ZHOU Yixiang, YU Jinglun, et al. Based on the optimization of CFD simulation ski jumping air flight posture and verification research [J]. Tribology, 2023, 43(10): 1151 − 1164. (in Chinese)
[14] NØRSTRUD H, ØYE I J. On CFD simulation of ski jumping [M]// PETERS M. Computational Fluid Dynamics for Sport Simulation. Berlin, Heidelberg: Springer, 2009: 63 − 82.
[15] 刘丹, 王虹, 马勇, 等. 滑雪服表面粗糙度对跳台滑雪飞行阶段气动特性的影响[J]. 北京服装学院学报(自然科学版), 2021, 41(4): 9 − 15. LIU Dan, WANG Hong, MA Yong, et al. Effects of the ski clothes’ surface roughness on the aerodynamic characteristics during flight in ski-jumping [J]. Journal of Beijing Institute of Fashion Technology (Natural Science Edition), 2021, 41(4): 9 − 15. (in Chinese)
[16] CHOWDHURY H, MORIA H, ALAM F, et al. Aerodynamics of ski jumping suits [J]. Sports Technology, 2011, 4(3/4): 164 − 170.
[17] ELFMARK O, ETTEMA G, GROOS D, et al. Performance analysis in ski jumping with a differential global navigation satellite system and video-based pose estimation [J]. Sensors, 2021, 21(16): 21165318. doi: 10.3390/s21165318
计量
- 文章访问数: 79
- HTML全文浏览量: 19
- PDF下载量: 14
