MULTI-SCALE LONG-SHORT TERM MEMORY NEURAL NETWORK METHOD FOR PREDICTING WIND PRESSURE ON COAL SHED SURFACE
-
摘要:
风荷载是影响大跨度空间结构安全性和稳定性的关键因素之一,因此研究结构表面风压对煤棚结构设计具有重要意义。风洞试验是获取煤棚结构表面风压的主要方法,但其存在成本较高和耗时较长的问题。利用风洞试验积累的大量数据发展风压快速预测方法是目前的研究热点之一。该文以长短期记忆(Long Short-Term Memory,LSTM)神经网络为基础,建立了煤棚结构风压时序预测模型,该模型利用高斯平滑将实验数据分为光滑数据和脉动数据,进而分别训练大尺度网络和小尺度网络。结果表明:所提出的多尺度网络预测模型可以实现对煤棚表面风压的快速预测,且相比于传统LSTM神经网络,多尺度LSTM神经网络具有误差小、精度高等优势。因此,基于LSTM的多尺度神经网络可以为煤棚等大跨空间结构表面风压提供依据。
Abstract:Wind loading is a crucial factor affecting the safety and stability of long-span space structures. Therefore, studying the surface wind pressure is important for the design of coal shed structures. The wind tunnel test is the main method for obtaining the surface wind pressure of coal shed structure. However, it is associated with high costs and time-consuming procedures. One of the current research hotspots to develop a rapid wind pressure prediction method is adopting the large amount of data accumulated from wind tunnel test. In this study, a time series prediction model for coal shed structure wind pressure is thusly established upon Long Short-Term Memory (LSTM) neural network. The model utilizes Gaussian smoothing to divide experimental data into smooth and pulsating data, and then trains large-scale and small-scale networks separately. The results show that the multi-scale network prediction model proposed can achieve the rapid wind pressure prediction on the surface of coal shed. Compared to traditional LSTM neural network, the multi-scale LSTM neural network demonstrates advantages such as lower error and higher accuracy. Therefore, the multi-scale network based on LSTM can provide a basis for predicting surface wind pressure for long-span spatial structures such as coal sheds.
-
Keywords:
- coal shed /
- LSTM /
- wind pressure prediction /
- neural network /
- long-span structure
-
随着技术、经济和文化的发展,建筑结构逐渐向高耸化、轻质化、大跨度的方向发展,被应用于体育场馆、工业厂房、车站等领域[1]。大跨空间结构也成为了近三十多年来发展最快的结构形式之一。由于大跨度结构的特殊性与风作用机理的复杂性,大跨度结构的风致效应十分复杂,因此风荷载影响分析是大跨度结构设计的一个重要方面,是此类结构设计的主控荷载之一[2]。
煤棚是典型的大跨度空间结构,具有质量轻、刚度弱、阻尼小等特点,因此对煤棚表面的风荷载和风压分布的研究具有重要意义[3 − 5]。目前研究煤棚表面风荷载特性的方法主要有风洞试验和数值模拟,其中比较流行的是数值模拟与风洞试验相结合,以得到更好的相互验证效果[2]。但是当利用风洞试验进行更为精细化的研究时,还存在一些问题;结构表面脉动风压的分析需要选用计算量较大的大涡模拟技术,因此面临着计算量和计算精度难以平衡的问题[2 − 5]。而且从大跨度空间结构的未来发展考虑,有必要研究非线性分析方法去分析和解决建筑抗风与稳定问题[2]。
随着计算机性能的提升和大数据方法的发展,深度学习方法凭借其非线性表征能力已经广泛应用于自然语言处理等许多领域[6]。随着数据库技术的发展及其在结构抗风领域的应用,将已有的研究数据与数据挖掘相结合对既有数据进行处理和应用成为一种趋势[7]。
循环神经网络(Recurrent neural network, RNN)相比一般的神经网络来说,考虑到了时间序列的相关性,能够处理序列变化的数据。但是RNN的长期记忆能力有限,在长序列训练过程中可能出现梯度消失和梯度爆炸等问题[8 − 11]。长短期记忆(Long short-term memory, LSTM)神经网络是RNN的一种变体,弥补了其可能出现的问题,在处理前后相互关联的时序数据时处于相对优势的地位[6]。CHEN等[12]基于美国NIST低矮房屋数据库,利用人工神经网络,对低矮双坡屋盖结构的平均风压和脉动风压进行了预测。傅继阳等[13]采用模糊神经网络预测了大跨度屋盖结构风压分布。苏宁等[7]建立了脉动风荷载参数的广义回归神经网络预测模型,建立了基于人工神经网络预测的抗风设计基本框架。WENG等[14]提出了一种基于机器学习的低层非孤立建筑风压预测模型(ML-WPP)和一种时程插值方法,凭借ML-WPP的优势减少了对物理风洞测试的依赖。LANG等[15]提出了一种改进的射频法用于风压预测,而且进一步的应用表明,改进后的模型可用于其他大跨度建筑风洞试验的风压分布预测。
此外,入射风向角、风湍流特性、上游地形粗糙度和周围环境等因素都会影响大跨度屋顶结构的风压分布,这些因素也会对数据的分析造成干扰。对于这种多因素叠加会加强噪声的数据,需要使用一些新的技术,例如多尺度方法来提高数据分析和模型的预测精度[16]。多尺度方法通过在不同尺度上对数据进行分析,可以更全面地理解数据的特征和结构,在一些领域得到了应用,例如信号处理、图像处理、模式识别等领域。CHEN等[17]提出了一种融合双向长短期记忆网络和多域分层解码的多尺度融合卷积神经网络,获得了综合能源系统数据的多尺度特征。LIN等[9]结合了时间窗、多尺度序列和LSTM结构的应用,提高了预测精度,提出了一种数据驱动框架来估计复杂系统的规则语言。岳杰顺等[16]以一维卷积网络(1DCNN)为基础,构建了一种编码—解码型网络结构,提出了一种多尺度深度学习网络。
因此,本文采用基于LSTM神经网络的预测方法针对煤棚结构的表面风压开展了研究,并提出了一种多尺度神经网络预测模型。本文研究内容如下:首先介绍了LSTM模型和相关计算公式;其次介绍了风洞试验、模型设计与数据集的构建;然后对模型的预测结果进行了分析与讨论;最后进行了总结和展望。
1 LSTM神经网络
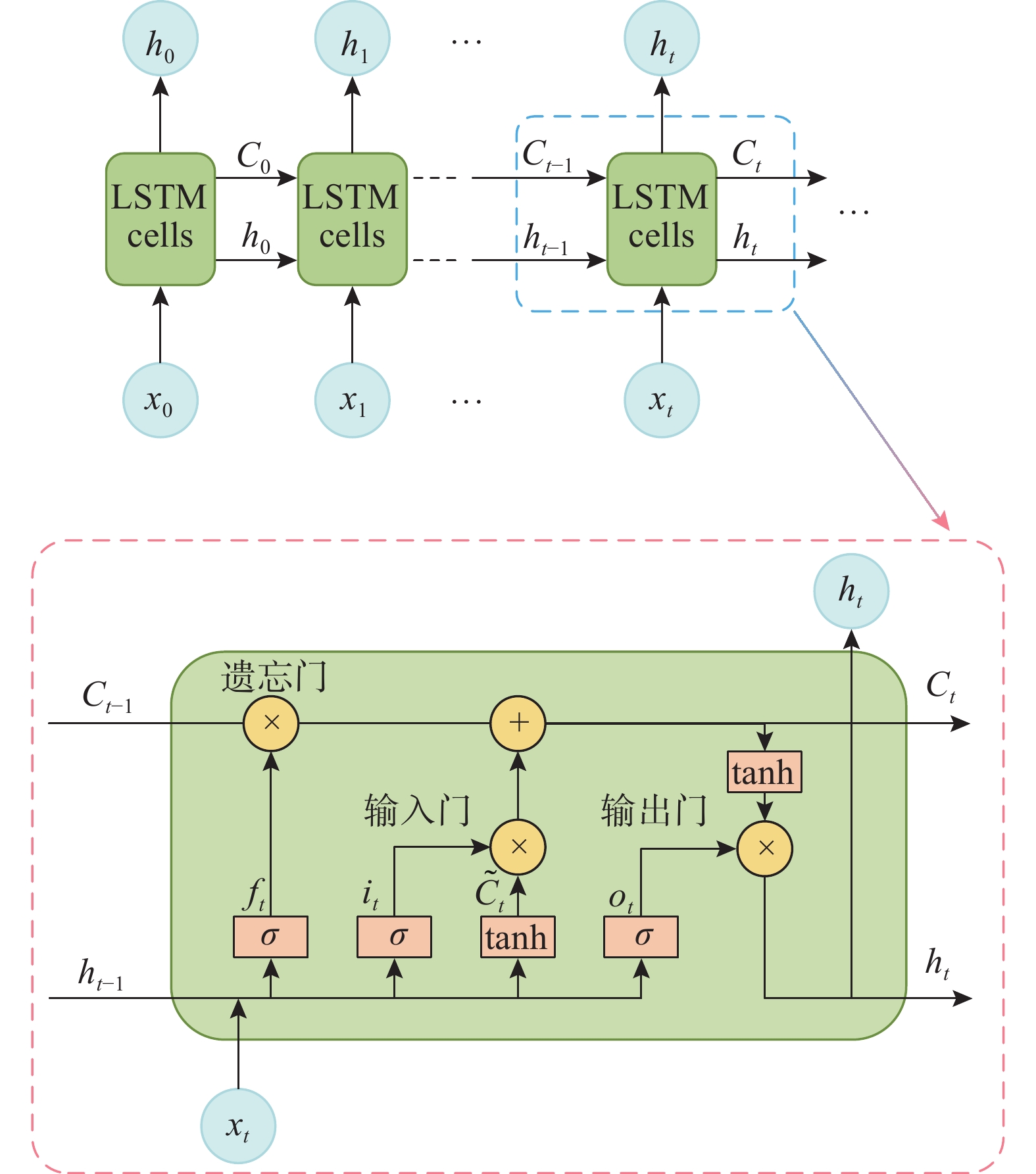
LSTM神经网络是一种特殊的RNN模型,是对传统RNN的改进,既具备长期记忆,又具备短期记忆,通过“门”控制将两者结合起来,这种特殊的结构设计可以有效避免长期依赖问题,因而更加稳定和适用[9],LSTM模型结构如图1所示。
LSTM的隐藏单元用于存储和传递信息,有3个门,分别为输入门、输出门和遗忘门,通过这些结构可以确定输入信息中的哪些数据将会被遗忘、保留和输出[9]。将t时刻隐藏层中的输入和输出向量分别定义为xt和ht,记忆单元为Ct,LSTM的前向计算过程见式(1)~式(6)。
遗忘门决定了记忆单元需要丢弃的信息:
{f}_{t}=\sigma ({\boldsymbol W}_{{\mathrm{f}}}\cdot \left[{h}_{t-1},{x}_{t}\right]+{\boldsymbol b}_{{\mathrm{f}}}) (1) 输入门决定需要更新的信息,并将此时产生的新信息加入到记忆单元中:
{i}_{t}=\sigma ({\boldsymbol W}_{{\mathrm{i}}}\cdot \left[{h}_{t-1},{x}_{t}\right]+{\boldsymbol b}_{{\mathrm{i}}}) (2) \tilde{{C}_{t}}=\mathrm{tanh}({\boldsymbol W}_{{\mathrm{c}}}\cdot \left[{h}_{t-1},{x}_{t}\right]+{\boldsymbol b}_{{\mathrm{c}}}) (3) 更新当前时刻记忆单元的内容,形成新的记忆:
{C_t} = {f_t} \odot {C_{t - 1}} + {i_t} \odot \widetilde {{C_t}} (4) 输出门确定记忆单元需要输出的信息:
{o}_{t}=\sigma ({\boldsymbol W}_{{\mathrm{o}}}\cdot \left[{h}_{t-1},{x}_{t}\right]+{\boldsymbol b}_{{\mathrm{o}}}) (5) {h}_{t}={o}_{t}\cdot \mathrm{tanh}({C}_{t}) (6) 式中:下标i、f、o分别为输入门、遗忘门、输出门; \sigma 为非线性激活函数; \boldsymbol W 为权重矩阵; \boldsymbol b 为偏置矩阵; \tanh 为双曲正切函数; {C_t} 为记忆单元; {h_{t - 1}} 和 {h_t} 为上一时刻和当前时刻LSTM细胞输出; {x_t} 为当前时刻网络的输入。
2 模型设计与数据集的构建
2.1 风洞试验
本研究以某实际煤棚为背景,在风洞中进行缩尺模型的测压试验,试验在石家庄铁道大学风工程研究中心STU-1风洞实验室低速试验段内进行,低速试验段宽4.4 m、高3.0 m、长24.0 m,最大风速达30.0 m/s。实际煤棚长640 m、宽206 m、高约52 m,模型的几何缩尺比为1∶250,本研究共在578个位置布置了双面测压点,其中煤棚顶部518个位置布置了测点,山墙118个位置布置了测点,天窗42个位置布置了测点,模型测点总数为1356个。安装在风洞中的试验模型如图2所示。
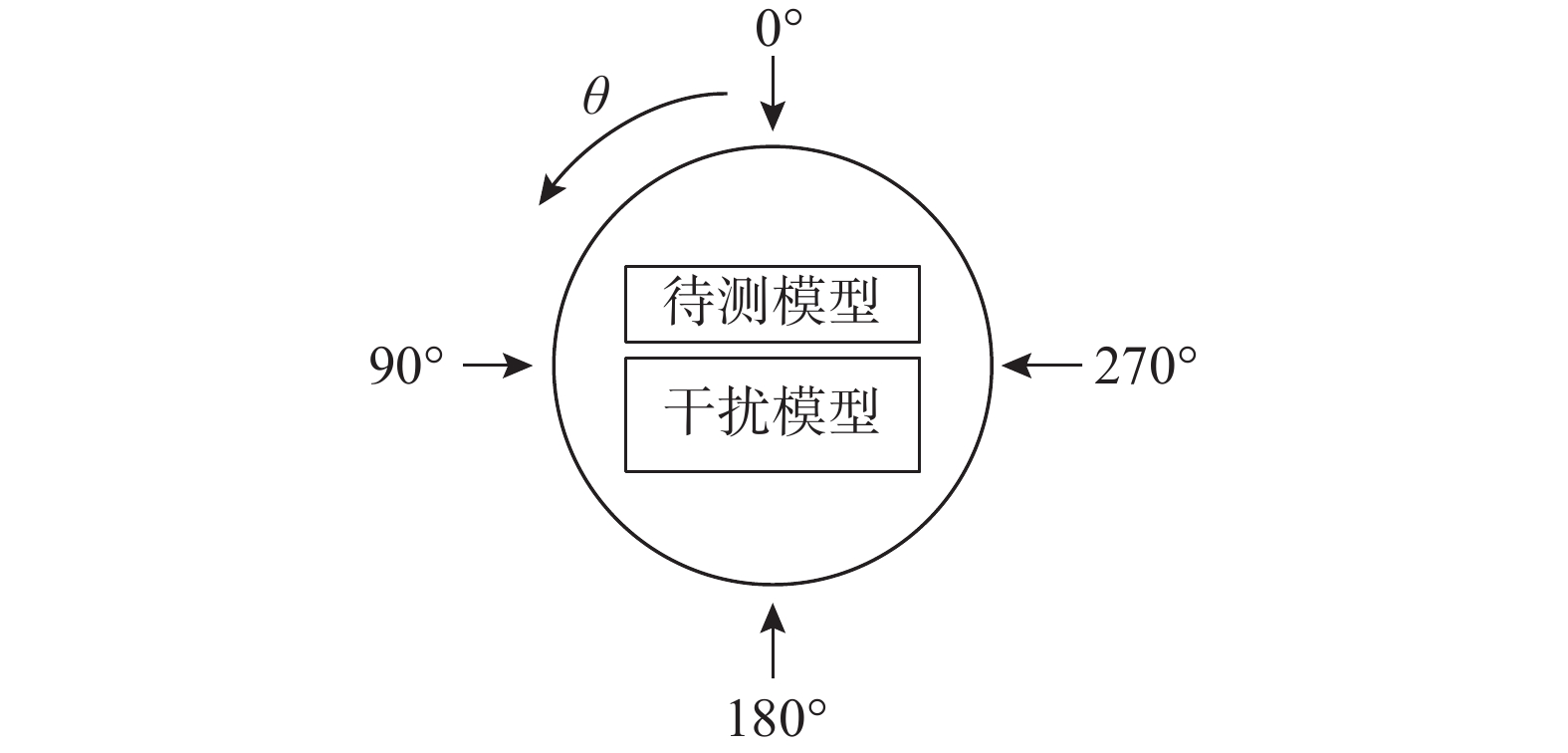
试验工况为B类地貌有干扰,试验自由来流风速为10 m/s,压力扫描阀的采样频率为330 Hz,采样时间为30 s。试验定义来流由垂直于网壳煤棚长轴方向为0º风向角,以10º风向角为间隔逆时针旋转。风向角范围0°~360°,定义如图3所示,风向角用θ表示。
2.2 模型设计
本研究基于开源Tensorflow库搭建LSTM网络框架,对处理好的数据进行网络训练。引入Dropout层减少模型过拟合,提高模型的泛化能力,因此该网络模型的隐藏层包含2个LSTM层、2个Dropout层和1个Dense层。共设置4个模型,具体结构如表1所示。本研究是对单变量进行时序预测,为了保证LSTM模型的准确性与鲁棒性,分别测试了20、40与60三种时间步长下的时序预测,LSTM模型的超参数选取如下:
① 优化器:选择Adam优化器;
② 学习率:对每个模型都设置4个学习率,分别是0.001、0.002、0.003与0.004;
③ 批大小:batch size设置为64;
④ 训练轮数:针对不同的学习率设置不同的训练轮数epoch。
为了进一步提高模型预测的精确性,将试验数据通过高斯平滑方法处理为光滑部分和脉动部分,进而针对两部分数据分别建立不同尺度的LSTM网络进行训练和预测。
表 1 LSTM模型分类Table 1. Classification of LSTM model模型 第1层LSTM
记忆体个数Dropout 第2层LSTM
记忆体个数Dropout 模型1 100 0.3 100 0.3 模型2 80 0.2 80 0.2 模型3 80 0.2 100 0.3 模型4 100 0.3 80 0.2 2.3 数据集建立
本研究所用的煤棚数据来源于风洞试验,经处理后画出不同风向角下的体型系数云图。根据不同风向角的云图、规范等,最终部分典型测点构建数据集。一个测点共有9900组数据,为了使训练效果更好,经处理后选择1650组数据构建数据集。将构建好的数据集按照8∶1∶1的比例分为训练集(0, 1250)、验证集(1251, 1450)和测试集(1451, 1650)。
2.4 模型的评价指标
为了更好地判断模型的效果,本研究使用均方误差(Mean square error, MSE)作为模型调参的依据(损失函数),均方根误差(Root mean square error, RMSE)和平均绝对误差(Mean absolute error, MAE)衡量模型预测效果的评价指标,计算公式如下:
{\mathrm{MSE}} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {{\hat y_i}}} \right)}^2}} (7) {\mathrm{RMSE}} = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i} - {{\hat y_i}}} \right)}^2}} } (8) {\mathrm{MAE}} = \frac{1}{m}\sum\limits_{i = 1}^m {\left| {{y_i} - {{\hat y_i}}} \right|} (9) 式中:m为样本总量;{y_i}为i时刻的真实值;\widehat {{y_i}}为i时刻的预测值。
3 预测结果分析
3.1 单个测点的预测结果
3.1.1 单LSTM预测结果
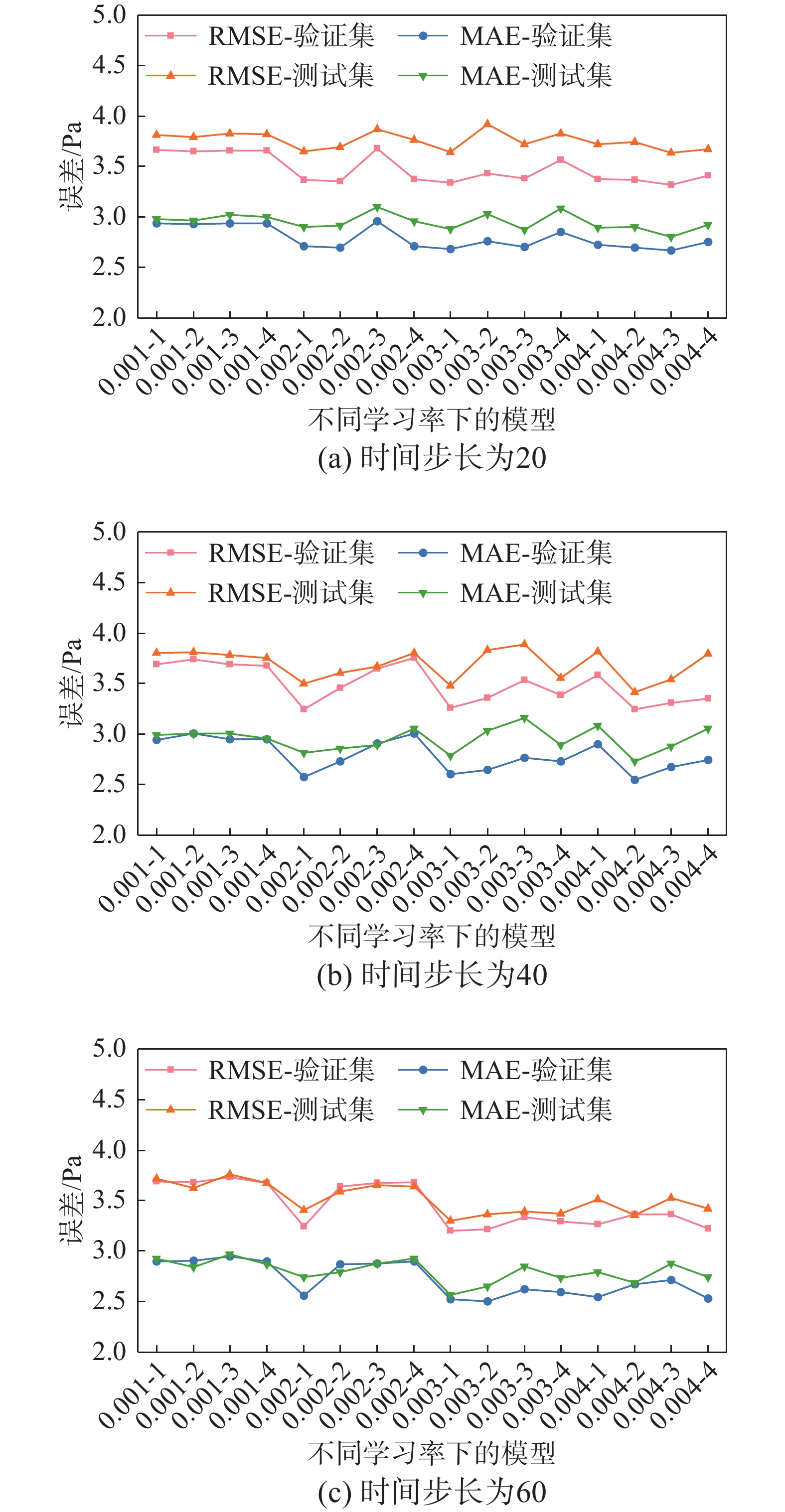
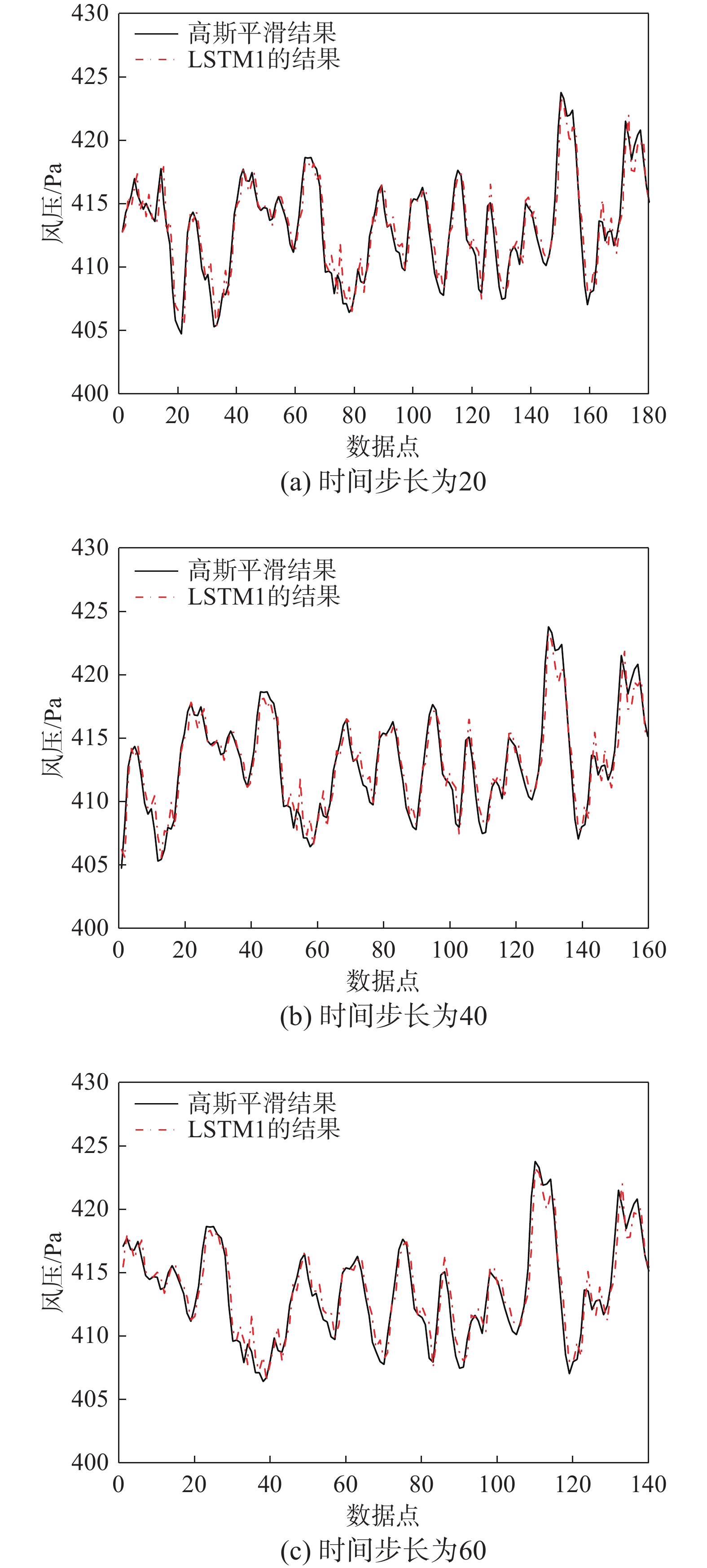
利用选择的典型测点数据对单LSTM模型进行训练,不同时间步下验证集与测试集的误差对比如图4(a)~图4(c)所示。选择不同时间步下的最优模型,绘制测试集的真实值与预测值对比图,如图5(a)~图5(c)所示。观察拟合结果,可以看出单LSTM模型在大多数点上的拟合效果优秀。模型真实值与预测值相差较小,振幅随时间变化较为吻合,预测效果较好。
3.1.2 多尺度神经网络预测结果
为了进一步提高模型的预测精度,首先利用高斯平滑方法将实验数据处理为光滑部分和脉动部分,然后分别建立不同尺度的LSTM模型进行训练。大尺度神经网络测试集训练结果分别如图6(a)~图6(c),由图6可以看出大尺度神经网络对光滑部分的预测效果优秀,能够更好地预测极值点的变化趋势,模型真实值与预测值相差较小,振幅随时间变化吻合。
不同时间步长下的小尺度网络测试集训练结果分别如图7(a)~图7(c),由图7可以看出LSTM模型捕捉到了曲线的变化趋势,对于小幅度震荡和幅值的预测效果也较好。
3.1.3 结果对比
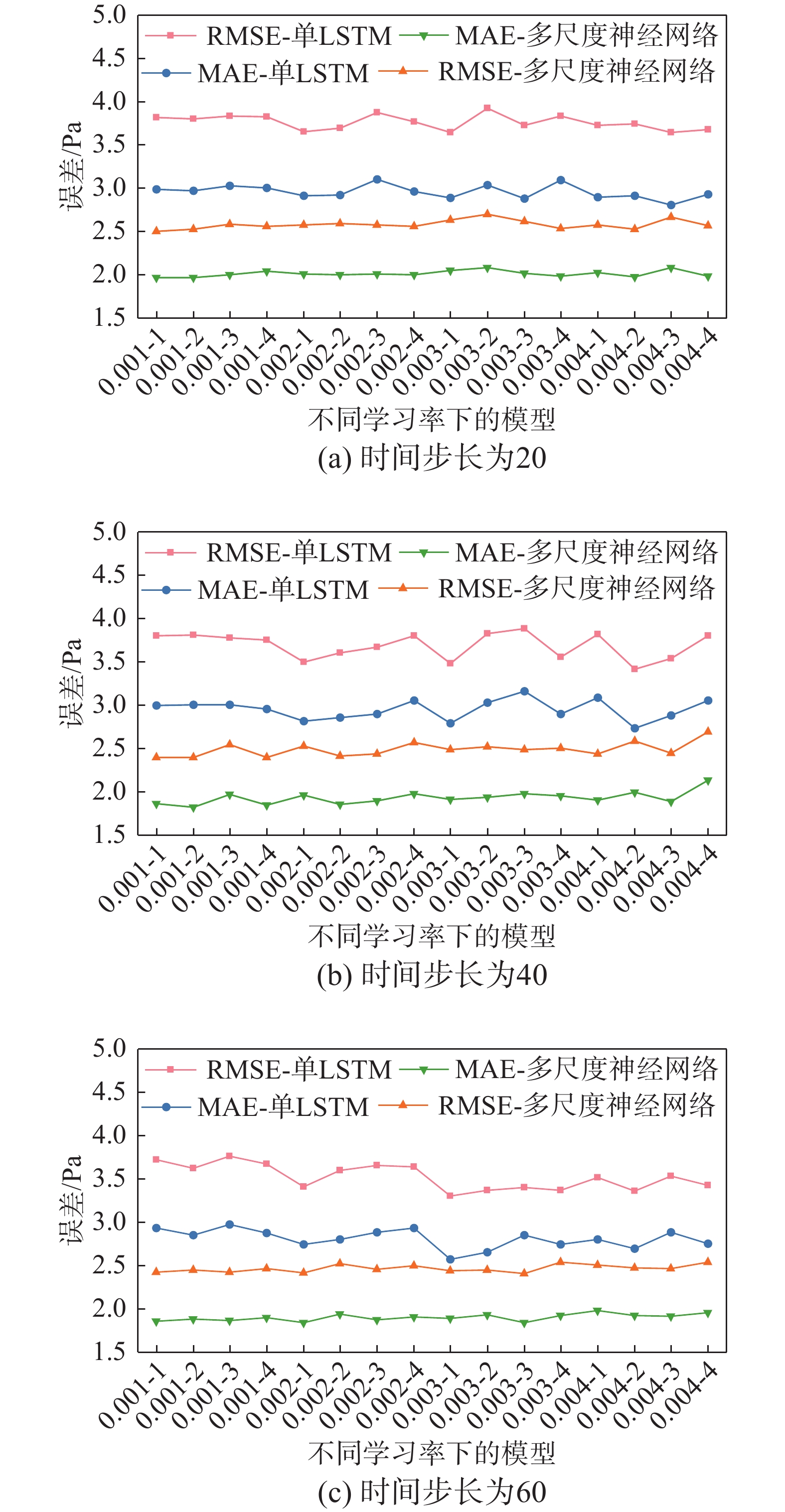
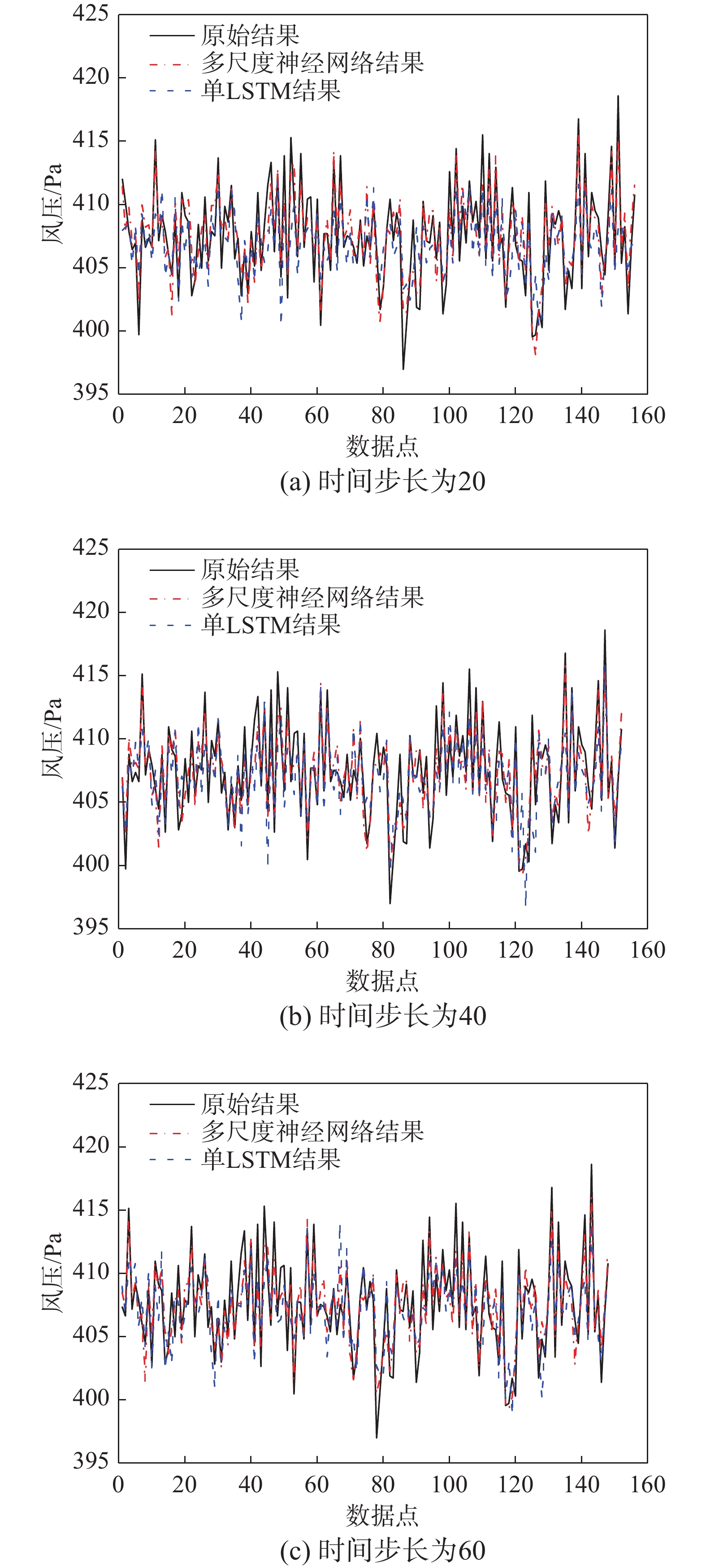
单LSTM预测模型和多尺度神经网络预测模型在不同时间步长下测试集的误差对比结果如图8(a)~图8(c)所示,并绘制模型训练后测试集的真实值与预测值对比图,如图9(a)~图9(c)所示。结合图8和图9可以看出,相比于单LSTM神经网络,多尺度神经网络可以更加精确地捕捉风压突变、震荡的频率和幅值,预测效果更优秀。
3.2 多个测点的多尺度神经网络预测结果
多尺度神经网络模型在单个测点上的表现较为优秀,因此在此基础上,结合多个测点对结构表面风压进行预测。单个LSTM预测模型和多尺度神经网络预测模型在不同时间步长下的测试集误差对比结果如图10(a)~图10(c)所示,训练后的真实值与预测值对比如图11(a)~图11(c)所示。结合图10和图11可以看出,相比于单个LSTM神经网络,多尺度神经网络模型的RMSE和MAE更小,预测效果更优秀,因此多个测点的风压预测具有可行性。
4 结论
本文基于LSTM神经网络,提出了一种可用于煤棚风压预测的多尺度神经网络预测方法,预测了单个测点和多个测点两种情况下的风压,得到的主要结论如下:
(1) 单LSTM网络和多尺度LSTM网络模型都能较好的逼近和预测风压;
(2) 与单LSTM网络相比,多尺度LSTM网络所获得的RMSE和MAE更低;
(3) 多尺度LSTM网络预测模型针对风压突变、震荡的频率和幅值的预测更加精确。
-
表 1 LSTM模型分类
Table 1 Classification of LSTM model
模型 第1层LSTM
记忆体个数Dropout 第2层LSTM
记忆体个数Dropout 模型1 100 0.3 100 0.3 模型2 80 0.2 80 0.2 模型3 80 0.2 100 0.3 模型4 100 0.3 80 0.2 -
[1] 陈伏彬, 唐宾芳, 蔡虬瑞, 等. 大跨平屋盖风荷载特性及风压预测研究[J]. 振动与冲击, 2021, 40(3): 226 − 232. CHEN Fubin, TANG Binfang, CAI Qiurui, et al. Wind load characteristics and wind pressure prediction of long-span flat roof [J]. Journal of Vibration and Shock, 2021, 40(3): 226 − 232. (in Chinese)
[2] 王俊, 赵基达, 蓝天, 等. 大跨度空间结构发展历程与展望[J]. 建筑科学, 2013, 29(11): 2 − 10. WANG Jun, ZHAO Jida, LAN Tian, et al. Development progress and future prospect of large-span spatial structures [J]. Building Science, 2013, 29(11): 2 − 10. (in Chinese)
[3] SONG J, XU W, HU G, et al. Non-Gaussian properties and their effects on extreme values of wind pressure on the roof of long-span structures [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 184: 106 − 115. doi: 10.1016/j.jweia.2018.11.027
[4] 孙一飞, 张磊杰, 刘庆宽, 等. 封闭形式对大跨度煤棚风荷载影响研究[J]. 工程力学, 2019, 36(增刊1): 234 − 239. doi: 10.6052/j.issn.1000-4750.2018.05.S046 SUN Yifei, ZHANG Leijie, LIU Qingkuan, et al. Study on the influence of closed form on wind load of long-span coal shed [J]. Engineering Mechanics, 2019, 36(Suppl 1): 234 − 239. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S046
[5] 郑怡彤, 吴倩云, 贾娅娅, 等. 考虑周边建筑影响的大跨煤棚风荷载体型系数研究[J]. 工程力学, 2021, 38(增刊1): 72 − 76. doi: 10.6052/j.issn.1000-4750.2020.05.S014 ZHENG Yitong, WU Qianyun, JIA Yaya, et al. Study on shape factor of wind load of large-span coal shed considering the influence of surrounding buildings [J]. Engineering Mechanics, 2021, 38(Suppl 1): 72 − 76. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.S014
[6] 刘庆宽, 刘士杰, 张珍, 等. 基于长短期记忆网络的桥梁非定常气动力预测[J]. 中国公路学报, 2023, 36(8): 56 − 65. LIU Qingkuan, LIU Shijie, ZHANG Zhen, et al. Unsteady aerodynamic prediction for bridges based on long short-term Memory Networks [J]. China Journal of Highway and Transport, 2023, 36(8): 56 − 65. (in Chinese)
[7] 苏宁, 彭士涛, 孙瑛, 等. 大跨度煤棚主体结构设计风荷载的神经网络建模研究及应用[J]. 建筑结构学报, 2019, 40(7): 34 − 41. SU Ning, PENG Shitao, SUN Ying, et al. Research and application on artificial neural network modeling of design wind load on large-span coal storage sheds [J]. Journal of Building Structures, 2019, 40(7): 34 − 41. (in Chinese)
[8] 杜晓庆, 鲁羿, 董浩天, 等. 基于长短期记忆神经网络的方柱表面风压时程预测[J]. 工程力学, doi: 10.6052/j.issn.1000-4750.2022.12.1072. DU Xiaoqing, LU Yi, DONG Haotian, et al. Prediction of wind pressure time series on square cylinder upon long short-term memory neural network [J]. Engineering Mechanics, doi: 10.6052/j.issn.1000-4750.2022.12.1072. (in Chinese)
[9] LIN R G, YU Y W, WANG H W, et al. Remaining useful life prediction in prognostics using multi-scale sequence and Long Short-Term Memory network [J]. Journal of Computational Science, 2022, 57: 101508.
[10] SABZIPOUR B, ARSENAULT R, TROIN M, et al. Comparing a long short-term memory (LSTM) neural network with a physically-based hydrological model for streamflow forecasting over a Canadian catchment [J]. Journal of Hydrology, 2023, 627: 130380. doi: 10.1016/j.jhydrol.2023.130380
[11] ZHANG Y K, RAGETTLI S, MOLNAR P, et al. Generalization of an Encoder-Decoder LSTM model for flood prediction in ungauged catchments [J]. Journal of Hydrology, 2022, 614: 128577.
[12] CHEN Y Z, KOPP G A, SURRY D. Interpolation of pressure time series in an aerodynamic database for low buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(6): 737 − 765. doi: 10.1016/S0167-6105(03)00006-0
[13] 傅继阳, 甘泉. 大跨平屋盖结构风压分布特性的神经网络模型[J]. 华南理工大学学报(自然科学版), 2003, 31(8): 62 − 66. FU Jiyang, GAN Quan. Neural network models for describing characteristics of wind pressure distribution on large span flat roof [J]. Journal of South China University of Technology (Natural Science Edition), 2003, 31(8): 62 − 66. (in Chinese)
[14] WENG Y M, PAAL S G. Machine learning-based wind pressure prediction of low-rise non-isolated buildings [J]. Engineering Structures, 2022, 258: 114148. doi: 10.1016/j.engstruct.2022.114148
[15] LANG L, TIANCAI L, SHAN A, et al. An improved random forest algorithm and its application to wind pressure prediction [J]. International Journal of Intelligent Systems, 2021, 36(8): 4016 − 4032. doi: 10.1002/int.22448
[16] 岳杰顺, 权晓波, 叶舒然, 等. 水下发射水动力的多尺度预测网络研究[J]. 力学学报, 2021, 53(2): 339 − 351. YUE Jieshun, QUAN Xiaobo, YE Shuran, et al. A multi-scale network for the prediction of hydrodynamics in underwater launch [J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(2): 339 − 351. (in Chinese)
[17] CHEN Z W, ZHAO W C, LIN X Y, et al. Load prediction of integrated energy systems for energy saving and carbon emission based on novel multi-scale fusion convolutional neural network [J]. Energy, 2024, 290: 130181. doi: 10.1016/j.energy.2023.130181
-
期刊类型引用(1)
1. 刘一诺,柴晓兵,孙一飞,褚泽楷,翟艳磊,贾娅娅,刘庆宽. 防风网对煤棚表面风荷载影响试验研究. 工程力学. 2025(S1): 105-110 .  本站查看
本站查看
其他类型引用(1)



 下载:
下载: