PERFORMANCE-BASED SEISMIC DESIGN METHOD OF A REINFORCED CONCRETE SELF-CENTERING FRAME WITH BEAM-END SPRING JOINTS
-
摘要:
梁端弹簧型自复位框架(self-centering frame, SCF)结构作为一种新型抗震结构体系，通过梁柱节点铰接构造来使整体结构抗侧刚度弱化，并在梁端设置钢板弹簧来给节点设定确定的转动刚度，从而达到地震作用下结构减震和震后结构自复位的目标。在已有理论和试验研究的基础上，对梁端弹簧型自复位框架的抗震设计方法进行了研究，并给出了此类结构的抗震性能水准以及结构的抗震设计流程。结合一幢三层自复位耗能框架结构的设计实例，进行基于性能的结构抗震设计，通过有限元模拟对该结构的动力响应与常规框架进行比较分析。结果表明：梁端弹簧型自复位耗能框架结构具有较小的加速度响应和层剪力响应，以及良好的变形性能。研究结果表明，梁端弹簧型自复位框架结构具有优越的抗震性能。
-
关键词:
- 梁端弹簧型自复位框架 /
- 基于性能的抗震设计方法 /
- 动力响应 /
- 抗震性能 /
- 有限元模拟
Abstract:As a new type of seismic structural system, self-centering frame (SCF) structure with beam-end spring joints weakens the lateral stiffness of the entire structure by adopting hinged beam-column joints. By setting leaf spring at the beam end, the rotational stiffness of joints can be quantificationally determined to achieve the goal of structural vibration reduction under earthquake and structural self-centering. Based on existing theoretical and experimental research, the seismic design method of SCF with beam-end spring joints is studied. Seismic performance level and structural seismic design process of this kind of structure are given. Combined with the design case of a three-story SCF with beam-end spring joints, the performance-based seismic design is carried out, and the dynamic response of the frame is compared with that of a conventional reinforced concrete frame (RCF) through finite element simulation. The analysis results show that SCF structure with beam-end spring joints has smaller acceleration response and shear response, as well as good deformation performance, which demonstrates that SCF with beam-end spring joints has superior seismic performance.
-
框架结构的梁柱节点在传递内力和保持结构整体性上具有十分关键的作用。在地震作用下，梁柱节点区承受着极大的内力，而且受力形式复杂，导致其成为了框架中最易受损的部位之一。传统抗震采用设置箍筋加密区增强梁柱节点强度的方法进行抗震设计，但这种方法会在地震后结构承重构件出现永久性塑性铰并产生较大的残余变形，地震后结构修复困难。
近年来，可恢复功能结构作为地震工程研究的一个方向，自复位结构[1 − 3]作为可恢复结构功能主要实现方法之一，通过自身的弹性恢复力使结构在受到地震作用后能恢复到原来的位置。自复位结构的概念于1991年在美国PRESSS研究计划中首次被提出[1]。1993年，PRIESTLEY和TAO[2]在此基础上提出自复位框架的概念。2009年，WOLSKI等[3]和CHOU等[4]提出了在框架梁上翼缘或者下翼缘安装耗散能量的摩擦装置，一系列的试验证明该系统具有良好的自复位和耗散能量的能力。2014年，吕西林等[5]对自复位钢筋混凝土框架结构进行了振动台试验，试验结果表明：结构具有良好的变形能力，地震作用后能恢复原位，且自复位构件上没有出现裂缝或损坏。蔡小宁等[6]提出了新型自复位预应力预制节点，对其进行低周反复加载试验表明，该节点具有较好的自复位能力和耗能能力。在上述国内外关于自复位结构研究的基础上，鲁亮等[7 − 8]提出了受控式钢筋混凝土摇摆框架结构及体外预应力自复位框架，并先后开展了抗震性能试验和分析研究，结果表明两类结构均具有优异的抗震性能和自复位能力。2019年，鲁亮等[9 − 10]提出了一种新型的抗震结构——梁端弹簧型自复位框架(self-centering frame, SCF)结构，并对其进行了试验研究。梁端弹簧型SCF通过在梁端设置钢板弹簧，实现结构在地震下自复位的目标；同时，在节点布置可更换的阻尼器，来控制结构位移和耗散地震能量，梁柱节点采用铰接构造使整体刚度弱化，从而实现结构的减震功能。模拟地震振动台试验结构表明，具有梁端弹簧型自复位耗能节点的框架结构具有良好的自复位能力和耗能能力，震后仅阻尼器发生屈服破坏，而主体结构梁柱无明显损伤。
本文以梁端弹簧型SCF为研究对象，探讨此类结构的抗震设计方法，并结合一幢3层梁端弹簧型SCF设计实例，进行基于性能的抗震设计方法研究，通过有限元模拟对该结构的地震响应与常规设计的钢筋混凝土框架(RCF)结构进行比较分析，验证该设计方法的有效性。
1 梁端弹簧型SCF结构
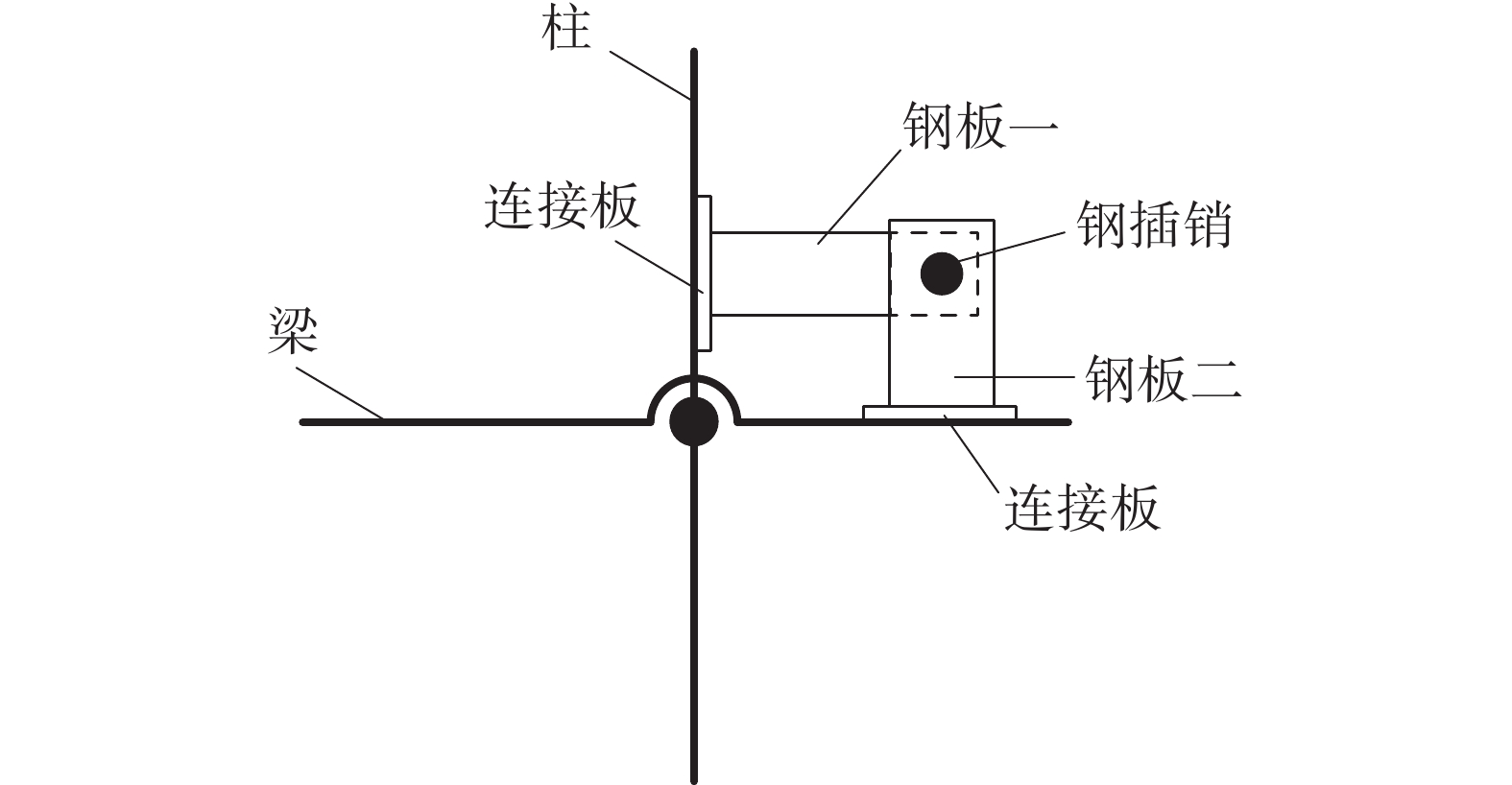
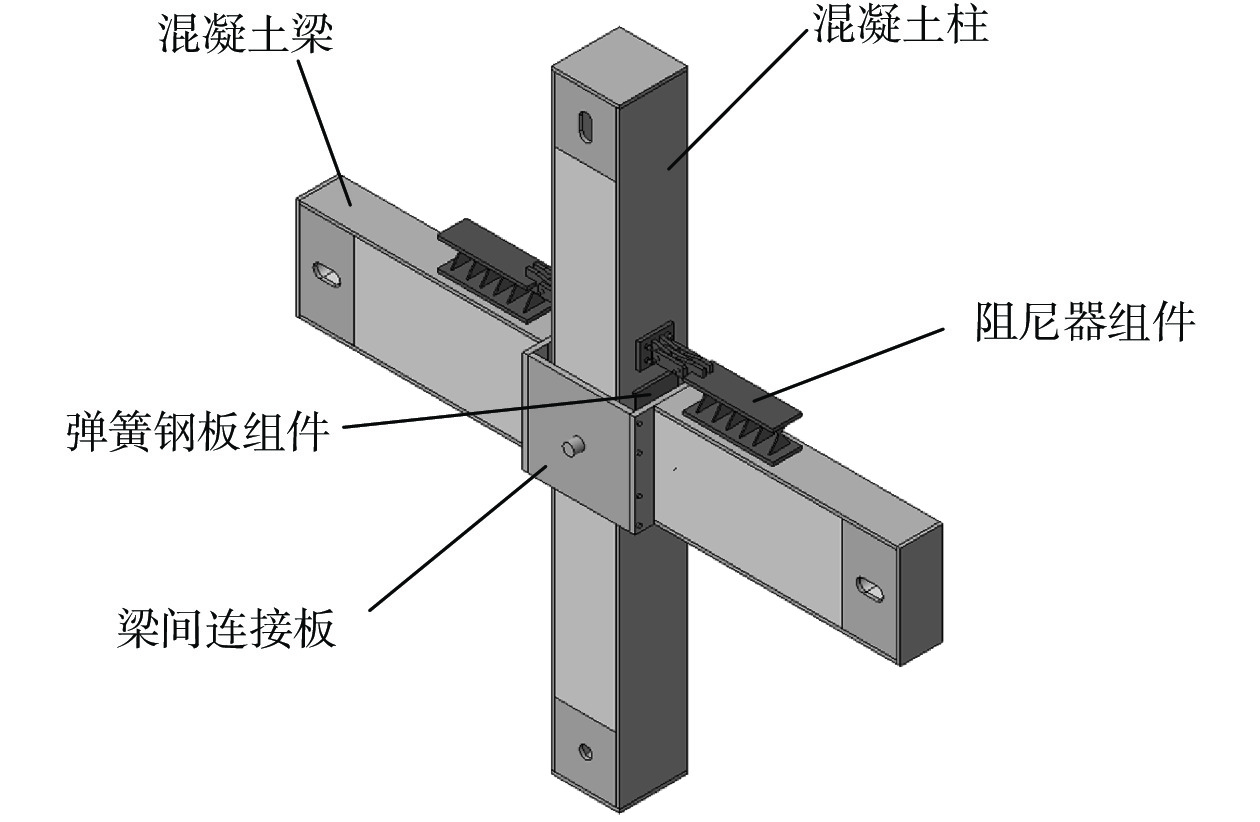
梁端弹簧型SCF节点是一类同时具备弹性恢复能力和耗能减震能力的新型节点形式，二维节点构造如图1所示。节点处柱为连续柱，两侧梁通过连接钢箱构成连续梁，两者通过钢插销铰接连接，梁端设置钢板弹簧与柱紧密贴合，梁柱之间布置了可更换阻尼器，此节点具有以下技术特征：
① 梁端弹簧型SCF结构的梁柱节点和柱脚节点均采用铰接构造。② 在节点附近设置弹性恢复装置，使得节点在发生转动时通过钢板弹簧的弹性变形提供的弹性恢复力来恢复到地震前原状。③ 通过预设钢板弹簧的刚度，使得节点具有确定的转动刚度，从而也确定了整体结构的抗侧刚度。④ 在梁柱之间设置阻尼耗能装置，用于能耗散输入的地震能量和控制结构的地震位移响应。⑤ 在梁柱之间设置类似剪切键的抗风和抗小震装置，该装置增加了结构刚度，使得结构在风荷载和多遇地震作用下不会产生过大的摇摆运动，满足结构的舒适度需求。在超过多遇地震以上烈度的地震作用下，剪切键破坏，结构抗侧刚度下降，结构产生摇摆运动。剪切键构造示意如图2所示。
SCF结构的阻尼器可以设置在结构上、下层之间，也可以设置在节点梁柱之间，图1所示为一种设置在节点区的X型软钢阻尼器。
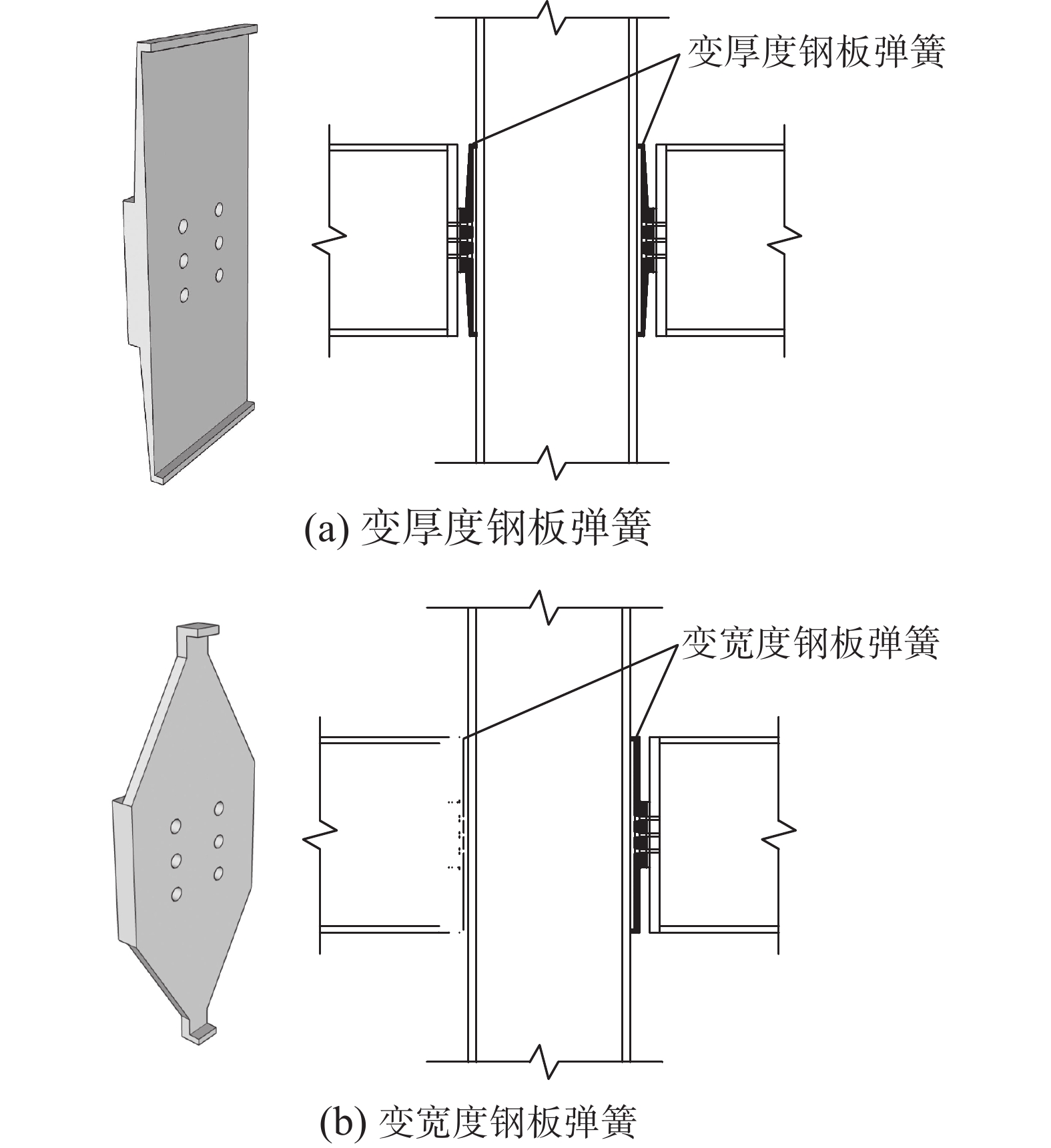
梁端弹簧提供节点确定的转动刚度。前期研究设计了2种钢板弹簧：变宽度和变截面厚度钢板弹簧，弹簧材料为60Si2Mn。弹簧形式如图3所示，弹簧紧密设置在梁端与柱之间，弹簧基座与梁端固定，承压端压紧在柱表面。
2 基于性能的抗震设计方法
2.1 抗震性能水准的确定
基于性能的抗震设计方法，是指设计结构时应该遵循不同水准地震下的性能目标，以此期望所设计的结构能够具有预期的抗震性能[11 − 14]。目前，结构性能水平的量化通常是用损伤指标来描述[15]。由于结构破坏主要是因为变形过大引起的，通常都采用位移指标。位移指标不但能够较好地反映结构构件的损伤程度，同时能够较好地控制非结构构件的性能水平，而位移指标中的“层间位移角”能够更加精确地体现结构的性能水平，从而在国内外被普遍使用。表1、表2列出了美国和中国[16 − 17]规范在抗震设计时对层间位移角限值的规定。
表 1 FEMA356不同性能要求的层间位移角Table 1. Inter-story drifts for different performance requirements in FEMA356结构类型 立即使用(IO) 生命安全(LS) 防止倒塌(CP) 混凝土框架 1/100 1/50 1/25 钢框架 1/143 1/40 1/20 带斜撑钢框架 1/200 1/67 1/50 混凝土剪力墙 1/200 1/100 1/50 表 2 GB 50011层间位移角限值Table 2. Inter-story drift limits in Chinese seismic design code结构类型 弹性变形 弹塑性变形 钢筋混凝土框架结构 1/550 1/50 钢筋混凝土框架-抗震墙、板柱-抗震墙、
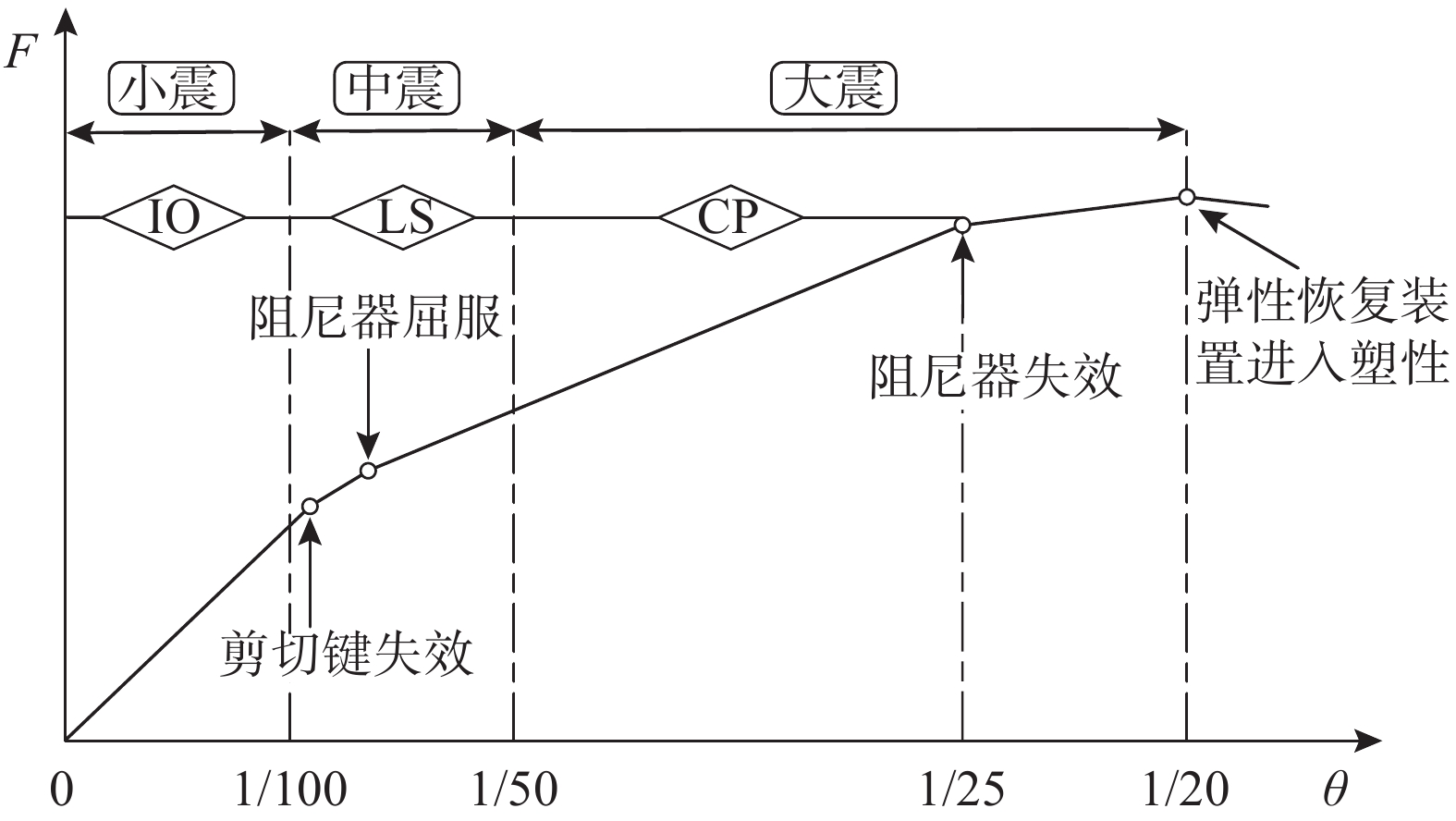
框架-核心筒1/800 1/100 钢筋混凝土抗震墙、筒中筒 1/1000 1/100 钢筋混凝土框支层 1/1000 1/120 多、高层钢结构 1/250 1/50 由于梁端弹簧型SCF结构为新型抗震结构体系，且节点采用确定刚度的铰接连接，结构刚度弱化程度较大，我国规范所规定的性能指标将不再适用，因此基于表1 FEMA356规定的层间位移角限值，在图4中给出了梁端弹簧型SCF结构在各地震水准下结构极限状态所对应的建议位移控制指标。
![]()
图 4 基于性能设计的层间位移极限状态Figure 4. Limit states of inter-story drift ratio based on performance design考虑到梁端弹簧型SCF结构具有更大的变形能力，在小震作用下，采用与FEMA356相同的立即入住(IO)限值，即层间位移角最大值为1/100；当结构遭遇中震时，节点处阻尼器屈服耗散大量地震输入能量，与常规设计的框架结构进入中震状态通过梁柱节点耗能类似，故在中震阶段采用与FEMA356相同的生命安全(LS)限值，即层间位移角最大值为1/50；当结构遭遇大震阶段后，耗能装置屈服破坏，结构具有更大的变形能力，仅依靠节点处弹性恢复装置提供结构复位能力，与FEMA356中的防倒塌限值1/25相比，结构具有更大的防倒塌位移限值，此限值根据弹性恢复装置的应力水平而定。为确保结构具有一定的安全储备，弹性恢复装置在设计时都留有一定的安全余量，因此将结构在罕遇地震下的层间位移角防倒塌限值定为1/20，与FEMA356规定的常规混凝土框架结构相比有所增大，体现了梁端弹簧型SCF结构具有更大的变形能力。
2.2 设计流程
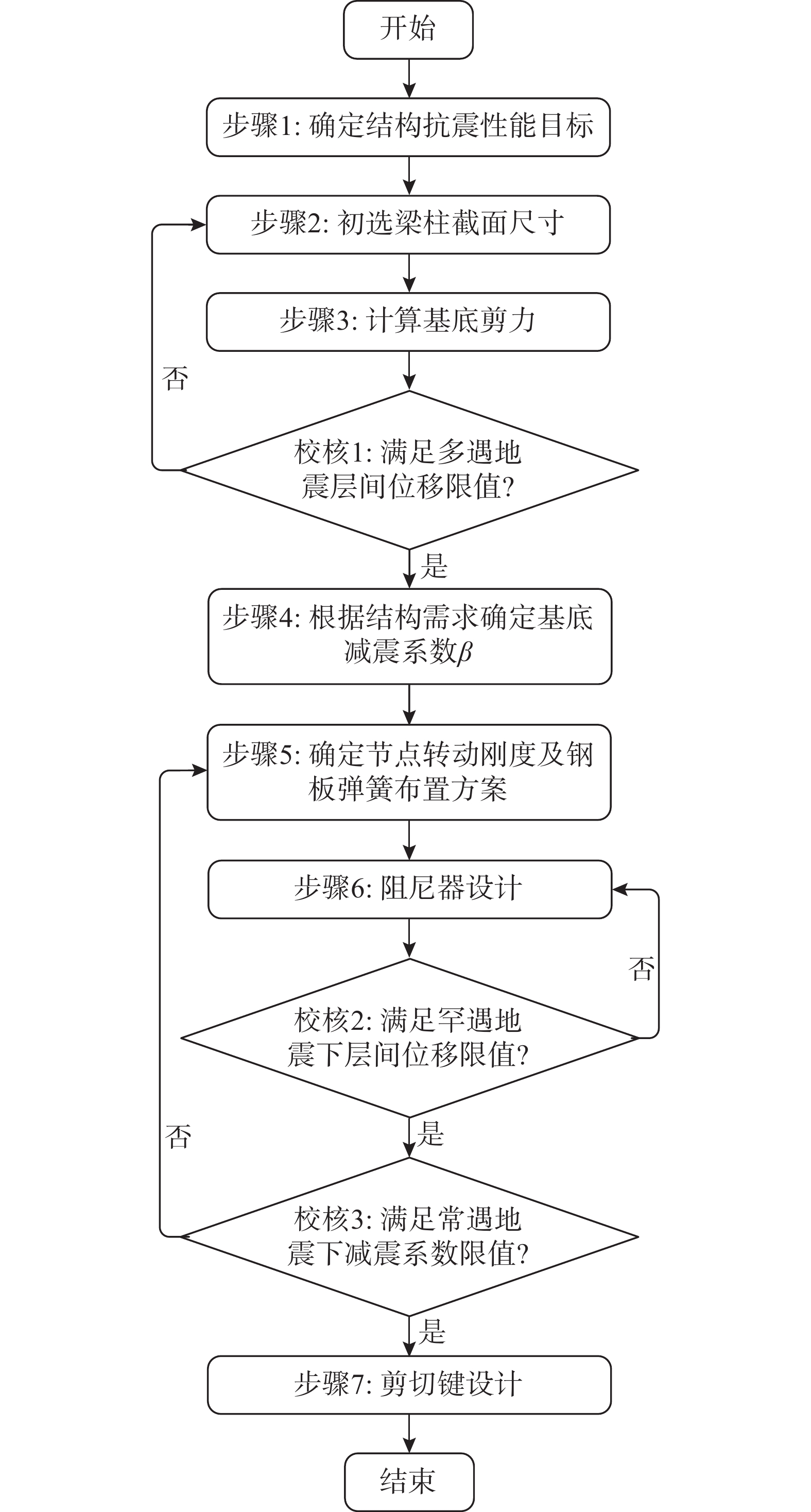
梁端弹簧型SCF结构为一类新型抗震结构体系，目前尚处于探索研究阶段。为实现该结构体系的实际工程应用，本节依据基于性能的抗震设计方法，给出了梁端弹簧型SCF结构的设计步骤：
1) 根据基于性能的抗震设计要求，包括规范条文、客户需求、成本要求等，确定结构的抗震性能指标，如结构层间位移、各层楼面加速度等。
2) 综合考虑建筑物的结构形式、场地类别以及抗震设防等级等因素，初步确定梁柱截面的尺寸，并统计荷载参数。
3) 利用反应谱法进行多遇地震作用下的弹性计算，计算得到与SCF建筑布置一致的常规RCF结构的基底剪力和层间位移，查看结构的层间位移角是否满足抗震设计规范的限值，若不满足，则需要重新调整梁柱截面尺寸。采用工程设计软件计算得到RCF构件截面配筋，同时将梁端弹簧型SCF结构的构件截面尺寸设计与RCF结构相同，构件配筋一般采用经过校核的截面构造配筋。
4) 基于梁端弹簧型SCF结构在地震作用下的结构性能需求，确定结构的整体刚度弱化程度，通过基底减震系数β量化。β定义为不同地震动作用下梁端弹簧型SCF结构的基底剪力响应与相应地震动作用下RCF结构基底剪力响应的比值。参考《建筑抗震设计规范》(GB 50011−2010)[17]对于隔震结构的规定，将隔震结构所受到的水平地震作用分为比非隔震结构降低半度、一度和一度半地震烈度3个档次，如表3所示。
表 3 水平向减震系数分档Table 3. Horizontal damping coefficient grading设防烈度(设计基本
地震加速度)水平向减震系数β 0.53≥β≥0.40 0.40>β>0.27 β≤0.27 9(0.40 g) 8(0.30 g) 8(0.20 g) 7(0.15 g) 8(0.30 g) 8(0.20 g) 7(0.15 g) 7(0.10 g) 8(0.20 g) 7(0.15 g) 7(0.10 g) 7(0.10 g) 7(0.15 g) 7(0.10 g) 7(0.10 g) 6(0.05 g) 7(0.10 g) 7(0.10 g) 6(0.05 g) 6(0.05 g) 5) 确定节点刚度及钢板弹簧的设计方案。根据第4)步的水平向减震系数β，求得梁端弹簧型SCF结构的节点刚度，进一步可确定钢板弹簧的力学性能参数和布置方案。此步计算方法依然采用多遇地震作用下的反应谱法，此步骤的结构计算模型不包括阻尼器。
6) 罕遇地震作用下阻尼器设计。根据梁端弹簧型SCF结构的节点转动刚度和节点最大转动角，确定金属阻尼器的初始刚度、屈服位移及屈服荷载。在设防地震和罕遇地震作用下，对加入阻尼器的结构模型进行动力时程分析，查看结构在设防地震下的减震系数是否还在规定的范围内，罕遇地震作用下结构的最大层间位移角是否符合要求、阻尼器是否发生破坏。若不满足，则调整阻尼器参数，重复以上分析步骤，直至满足要求，最终确定阻尼器布置方案。若调整阻尼器参数无法达到预期设计目标，则回到步骤5)，调整结构节点刚度，即梁端弹簧力学参数重新计算，直至满足设计要求。
7) 剪切键(抗风和小震装置)设计。梁端弹簧型SCF结构在梁柱之间设置了剪切键，此装置可以保证节点在小震作用下有较大的刚度。在结构受到风荷载和小震作用时，剪切键为自复位节点提供附加刚度，减小结构的变形，满足建筑使用的舒适度要求。通过计算需求刚度来设计剪切键。
据此梁端弹簧型SCF结构的设计流程图如图5所示。
3 设计实例
3.1 工程概况
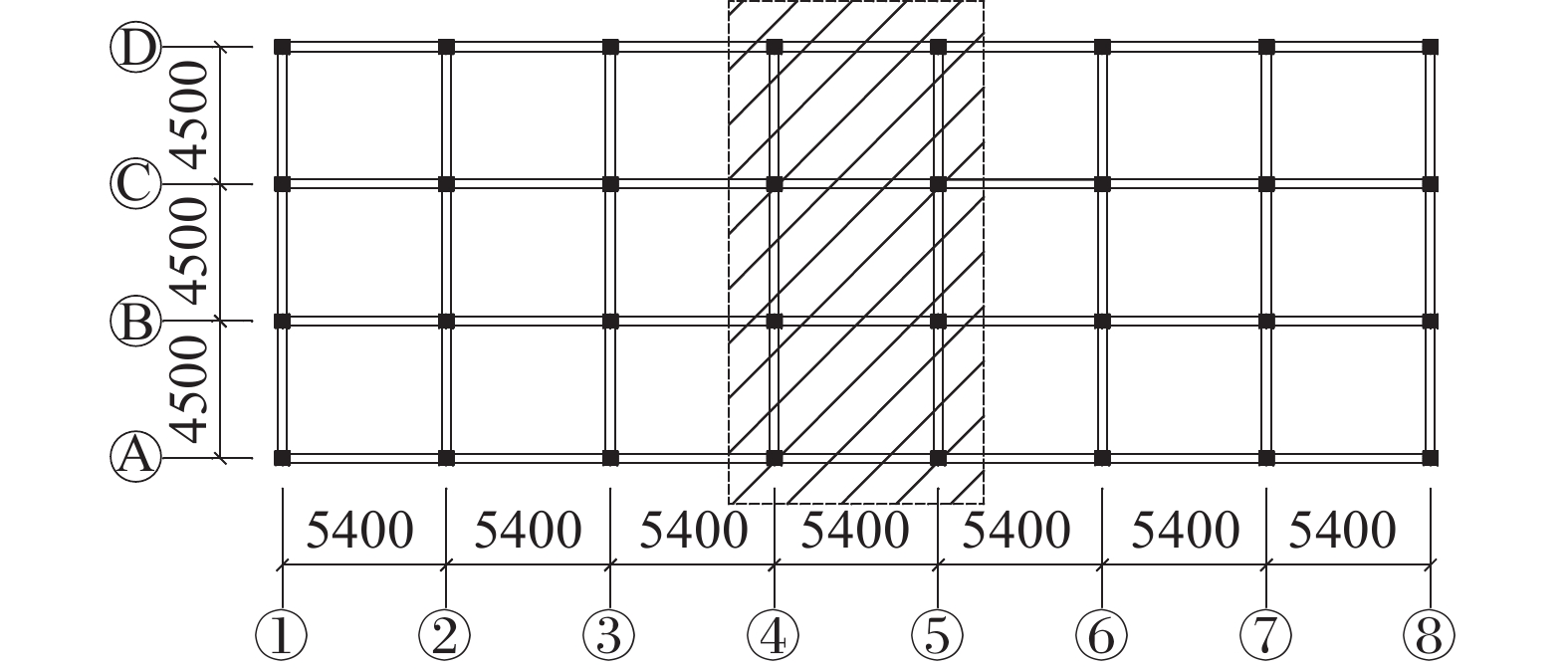
为了全面了解梁端弹簧型SCF结构的抗震性能和抗震设计流程，对一幢3层梁端弹簧型SCF结构进行抗震设计，计算方法采用动力时程分析法。设计原型为一个3层的框架结构，结构层高为3.6 m、总高10.8 m。横向共3跨、每跨4.5 m，纵向共7跨、每跨5.4 m。作为研究算例，取阴影部分处纵向1跨、横向3跨为计算单元进行平面框架结构分析，结构平面布置图与计算单元的选取如图6所示。为了对比分析梁端弹簧型SCF结构的抗震性能，并分析阻尼器的耗能减震效果，建立整体尺寸和截面尺寸完全相同的3个有限元模型：常规设计RCF、梁端弹簧型SCF无控结构(未设置节点耗能阻尼器)和有控结构(设置节点耗能阻尼器)，结构设计抗震设防烈度8度、设防地震地面加速度峰值为0.2 g。
![]()
图 6 框架结构平面布置图与计算单元选取 /mmFigure 6. Layout and calculation unit selection of frame structure初步选定构件截面尺寸：梁截面为300 mm×450 mm，柱截面为450 mm×450 mm，每层楼板厚均为120 mm，楼面均布活荷载2.0 kN/m2，屋面为不上人屋面，屋面活荷载为0.5 kN/m2，混凝土强度等级C40，钢筋强度等级HRB400。参照《建筑抗震设计规范》(GB 50011−2010)[16]要求对梁端弹簧型SCF进行构造配筋，常规框架的梁柱配筋使用PKPM软件进行设计。
根据对RCF结构试算，得到第1层~3层的重力荷载代表值分别为1039 kN、1039 kN、908 kN。利用反应谱法计算得到结构在多遇地震下的基底剪力和层间位移角，计算得到的RCF结构各层层间位移角小于抗震结构设计规范中的限值，梁柱截面尺寸满足承载要求。
设计基本地震加速度为8度(0.2 g)，设定水平地震作用比非隔震结构降低0.5度~1度，其对应水平向减震系数0.4≥β≥0.27。利用有限元时程分析对结构进行试算，参考文献[10]，可得到梁端弹簧型SCF结构的节点转动刚度范围为[0.4, 1.0][10]，从而最终确定钢板弹簧及金属阻尼器相关参数，如表4所示。
表 4 钢板弹簧及金属阻尼器参数Table 4. Parameters of leaf spring and metal damper结构 钢板弹簧转动刚度/((kN·m)/rad) 阻尼器 梁柱中
节点梁柱边
节点柱脚
节点初始刚度/
(kN/mm)屈服力/
kN屈服位移/
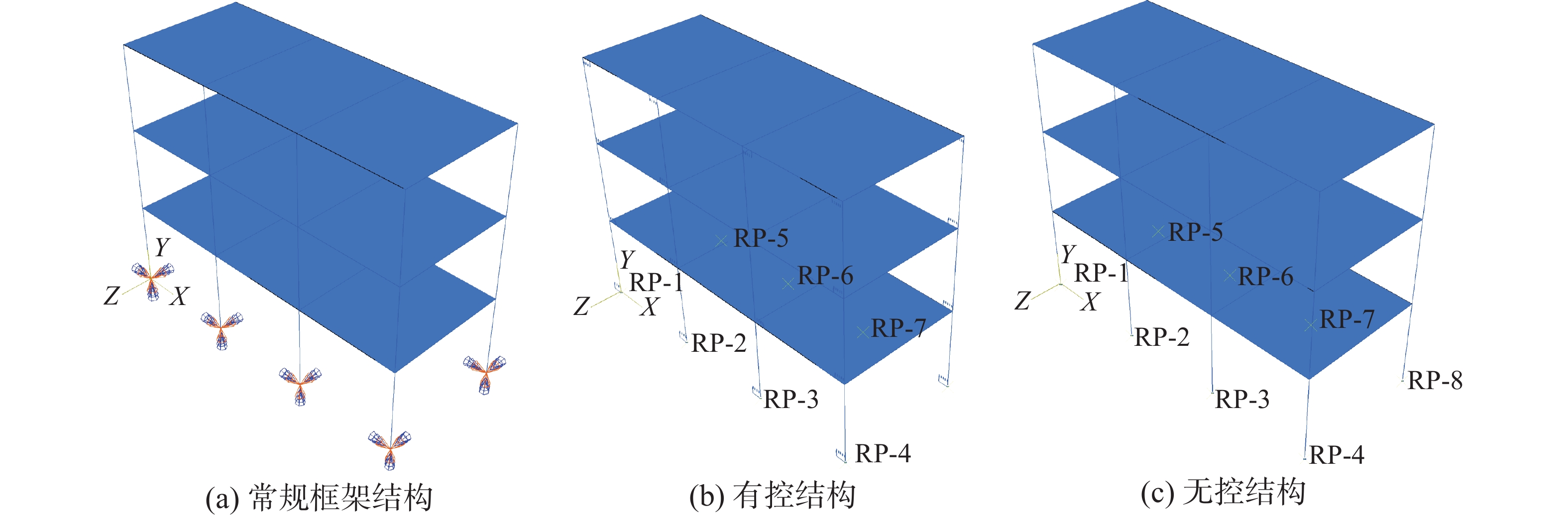
mm有控结构 800 400 800 12.5 30 2.4 无控结构 800 400 800 − − − 利用ABAQUS软件进行动力时程分析，分别建立常规框架、无控结构及有控结构有限元结构模型。模型梁柱采用B31单元，转动刚度通过Hinge连接单元模拟，阻尼器利用Axial连接单元模拟，楼板采用S4R单元模拟，钢筋混凝土本构采用吴晓涵基于ABAQUS开发的一组材料单轴滞回本构模型——TJ-Fiber[18]，3个有限元模型见图7。
3.2 地震动选取
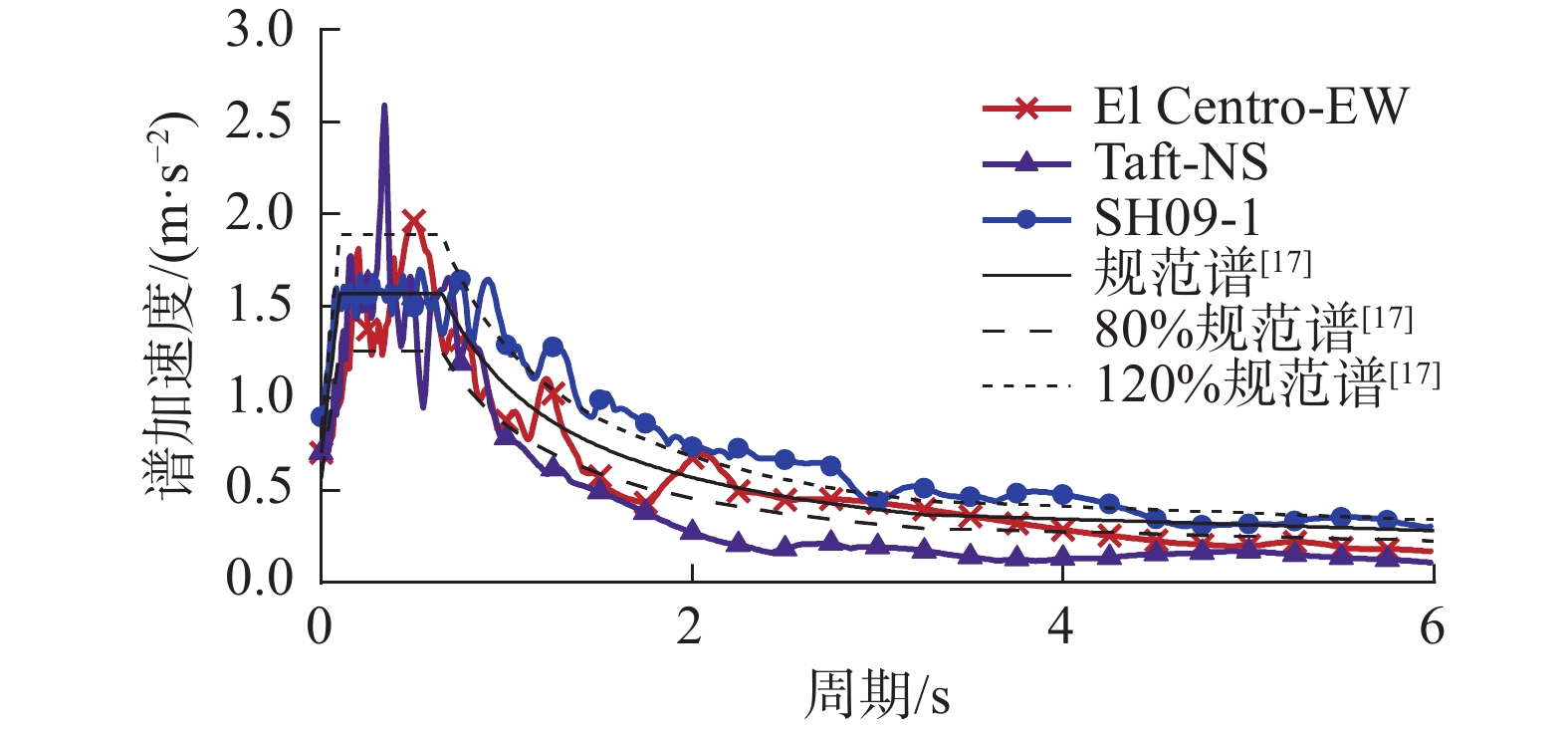
本文选取El Centro-EW波、Taft-NS波及上海人工波SH09-1三条地震波，对常规框架结构、无控结构、有控结构进行弹塑性时程分析，地震波信息见表5。图8为三条地震波加速度反应谱，由图8可见，三条地震波的能量涵盖了设计规范谱±20%的范围，与规范谱在统计意义上相符。
表 5 地震波信息Table 5. Information of seismic wave地震波 震级 时间 PGA/gal 持续时间/s 场地 El Centro-EW 7.1 1940 210.1 54.38 Ⅱ Taft-NS 7.7 1957 152.7 53.38 Ⅲ SH09-1 — — — 40.00 Ⅳ 3.3 结构自振特性
用ABAQUS数值模拟计算，得到常规框架结构、梁端弹簧型SCF无控结构及有控结构在X方向的前3阶自振周期，见表6所示。由表6可以看出，节点刚度弱化使得结构整体刚度显著降低，结构自振周期变大，无控结构、有控结构的第一平动周期分别约为常规框架结构的10倍和5倍。结构底部剪力随自振周期增大而减小，说明梁端弹簧型SCF结构有很显著的减震效果。但同时，结构的位移响应会随着自振周期的变大而增大，造成结构发生较大的层间位移。为此，有控结构在节点处设置阻尼器控制结构变形，结构刚度有所提高，自振周期减小，位移响应值的大小处于常规框架结构与无控结构之间。
表 6 结构前3阶自振周期Table 6. The first three natural vibration periods结构类型 三阶自振周 T1/s T2/s T3/s 常规框架 0.3130 0.0964 0.0549 无控SCF 3.1027 0.2349 0.0747 有控SCF 1.6917 0.2108 0.0729 3.4 结构地震响应
将El Centro-EW、Taft-NS及上海人工波地震动时程曲线，输入到常规框架结构、梁端弹簧型SCF无控结构及有控结构中，加速度峰值分别取0.07 g、0.2 g、0.4 g，模拟框架结构在多遇地震、设防地震和罕遇地震作用下的结构响应。
3.4.1 结构位移响应
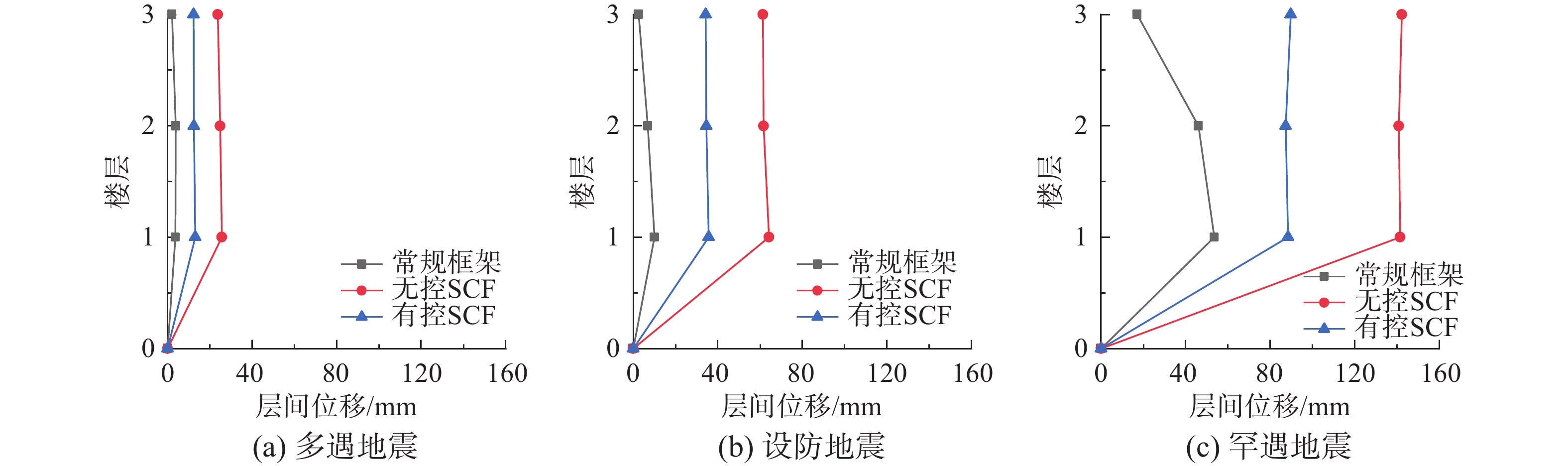
常规框架结构、梁端弹簧型SCF无控结构及有控结构在三条波下的层间位移响应见表7所示。限于篇幅，图9仅给出了三种结构在El Centro-EW波作用下的层间位移响应。
表 7 地震动下的位移响应Table 7. Displacement responses under ground motions峰值地面
加速度/g地震波 El Centro-EW Taft-NS SH09-1 楼层 F1/mm F2/mm F3/mm F1/mm F2/mm F3/mm F1/mm F2/mm F3/mm 0.07 常规框架 3.74 3.88 2.01 3.63 3.59 1.57 3.49 3.55 2.03 无控SCF 25.63 24.84 23.67 23.41 21.55 21.71 23.11 22.29 23.96 有控SCF 13.01 12.42 12.34 11.27 10.72 10.22 15.69 15.51 14.76 0.20 常规框架 10.10 6.90 2.50 12.60 10.89 4.10 10.10 11.80 6.20 无控SCF 64.21 61.72 61.33 50.16 49.68 49.61 65.66 67.39 65.86 有控SCF 35.71 34.54 34.24 30.10 28.38 27.67 46.89 47.92 46.04 0.40 常规框架 53.49 46.11 17.00 32.78 34.62 17.29 75.69 45.86 14.66 无控SCF 141.50 140.90 142.30 85.90 83.70 84.20 179.70 182.40 182.80 有控SCF 88.45 87.37 89.68 45.10 42.90 43.00 112.30 113.20 114.00 由表7和图9可以看出：① 在同等地震作用下，梁端弹簧型SCF有控结构和无控结构的层间位移远大于常规框架结构；② 多遇地震和设防地震下，无控结构最大层间位移角分别为1/140、1/53，有控结构最大层间位移角分别为1/229、1/75，均小于对应的层间位移角设计限值1/100和1/50；③ 无控结构在El Centro波、Taft-NS波和SH09-1波罕遇地震作用下，相应的最大层间位移角分别为1/25、1/42、1/20，有控结构分别为1/40、1/80、1/32，均能够满足结构罕遇地震下层间位移角限值1/20的性能要求。但是增设阻尼器后，有控结构位移分别减少了38.0%、48.9%、37.9%，说明增设阻尼器有效地控制了结构变形，使得结构在罕遇地震作用的层间位移得以控制。
![]()
图 9 El Centro-EW波作用下结构层间位移响应Figure 9. Inter-story drifts of structures under El Centro-EW earthquake3.4.2 结构层间剪力响应
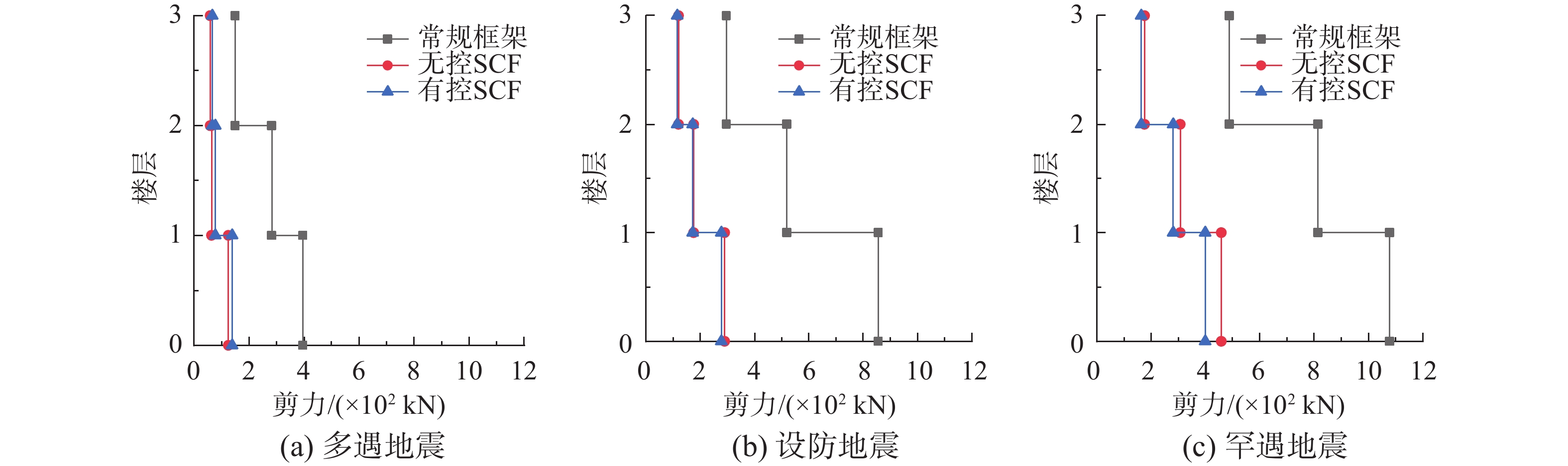
常规框架结构、梁端弹簧型SCF无控结构及有控结构在三条波下的层间剪力响应见表8所示。图10给出了结构在El Centro-EW波作用下的层间剪力响应。
表 8 地震动下的层间剪力响应Table 8. Inter-story shear responses under ground motions峰值地面加速度/g 地震波 El Centro-EW Taft-NS SH09-1 楼层 F1/kN F2/kN F3/kN F1/kN F2/kN F3/kN F1/kN F2/kN F3/kN 0.07 常规框架 395.3 283.2 148.9 379.6 263.0 147.5 318.2 262.8 157.3 无控SCF 125.2 64.3 59.1 97.6 61.0 38.8 112.5 78.4 65.1 有控SCF 138.0 77.0 65.7 106.3 64.9 43.7 122.9 89.3 76.5 0.20 常规框架 855.2 519.9 296.1 710.9 430.8 253.7 740.7 476.8 264.1 无控SCF 289.6 176.4 119.7 263.4 172.0 114.2 276.8 206.2 152.5 有控SCF 277.8 172.8 115.2 250.8 164.7 105.6 267.9 198.5 145.7 0.40 常规框架 1078 814.8 488.6 944.1 765.9 466.4 814.5 641.9 481.6 无控SCF 458.3 307.7 176.4 419.3 305.0 152.6 431.6 345.1 289.3 有控SCF 398.6 281.4 163.9 390.3 286.4 129.6 410.5 322.7 250.7 ![]()
图 10 El Centro-EW波作用下结构层间剪力Figure 10. Inter-story shear forces of structures under El Centro-EW earthquake由表8和图10可以看出：① 梁端弹簧型SCF结构在地震作用下的层间剪力均大幅降低，在多遇地震、设防地震、罕遇地震下的梁端弹簧型SCF有控结构基底剪力平均降幅分别为66.2%、65.4%、57.1%，无控结构分别为69.1%、63.9%、53.4%，减震效果明显；② 在三种设防地震波作用下的梁端弹簧型SCF有控结构的基底总剪力峰值分别为常规框架结构的32.5%、35.3%、36.2%，无控结构分别为常规框架结构的33.9%、37.1%、37.4%，均满足β在[0.27, 0.40]区间的设计要求。
3.4.3 结构加速度响应
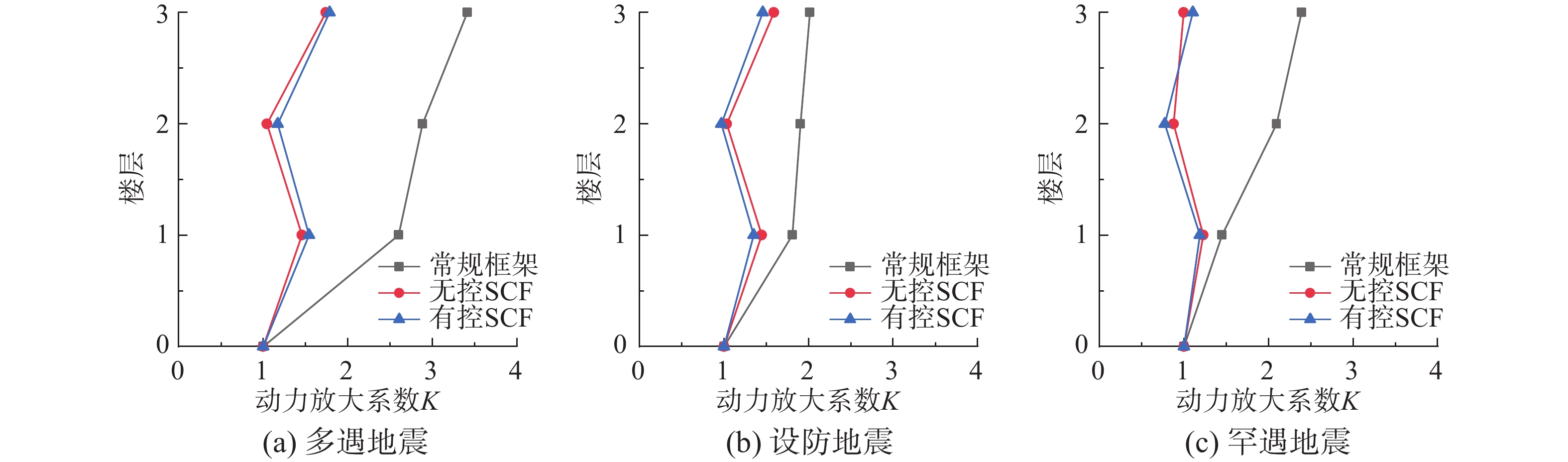
常规框架结构、梁端弹簧型SCF无控结构及有控结构在三条波下的层间加速度响应见表9所示。为了方便比较，采用动力放大系数K对三种结构的加速度响应进行比较。图11为结构在El Centro-EW波作用下的层动力放大系数K值。
表 9 地震动下的加速度响应K值Table 9. Acceleration responses K under ground motions响应参数 峰值地面加速度/g 地震波 El Centro-EW Taft-NS SH09-1 楼层 F1 F2 F3 F1 F2 F3 F1 F2 F3 加速度响应/(m∙s−2) 0.07 常规框架 1.82 2.02 2.39 1.76 2.05 2.53 1.51 1.92 2.47 无控SCF 1.02 0.73 1.22 1.19 0.65 1.12 1.28 0.96 1.47 有控SCF 1.08 0.82 1.25 1.28 0.77 1.30 1.33 1.05 1.58 0.20 常规框架 3.62 3.81 4.03 3.92 4.76 5.85 3.92 4.76 5.85 无控SCF 2.89 2.06 3.18 3.66 2.41 3.80 3.66 2.41 3.80 有控SCF 2.70 1.94 2.92 3.44 2.38 3.68 3.44 2.38 3.68 0.40 常规框架 5.80 8.39 9.56 5.73 6.93 8.59 5.21 6.95 7.21 无控SCF 4.91 3.50 3.98 6.82 4.55 6.73 6.92 4.88 6.90 有控SCF 4.75 3.09 4.41 6.77 4.34 6.78 6.42 4.43 6.75 动力放大系数K 0.07 常规框架 2.60 2.89 3.41 2.51 2.93 3.61 2.16 2.74 3.53 无控SCF 1.46 1.04 1.74 1.70 0.93 1.60 1.83 1.37 2.10 有控SCF 1.54 1.17 1.79 1.83 1.10 1.86 1.90 1.50 2.26 0.20 常规框架 1.81 1.91 2.02 1.96 2.38 2.93 1.96 2.38 2.93 无控SCF 1.45 1.03 1.59 1.83 1.21 1.90 1.83 1.21 1.90 有控SCF 1.35 0.97 1.46 1.72 1.19 1.84 1.72 1.19 1.84 0.40 常规框架 1.45 2.10 2.39 1.43 1.73 2.15 1.30 1.74 1.80 无控SCF 1.23 0.88 1.00 1.71 1.14 1.68 1.73 1.22 1.73 有控SCF 1.19 0.77 1.10 1.69 1.09 1.70 1.61 1.11 1.69 ![]()
图 11 El Centro-EW波作用下加速度响应Figure 11. Acceleration response under El Centro-EW earthquake由表9和图11可以看出：① 梁端弹簧型SCF有控结构和无控结构的各层加速度动力放大系数基本一致；② 在地震作用下，梁端弹簧型SCF结构的动力放大系数明显小于常规框架结构，说明采用梁端弹簧型SCF结构可以有效减小结构的动力响应。
综合比较常规框架结构、梁端弹簧型SCF无控结构和有控结构在3条地震波作用下的结构动力响应可以发现：增设节点阻尼器后的有控结构能很好地控制结构位移响应，同时不会带来结构剪力响应和加速度响应的显著增加。
4 结论
本文提出了梁端弹簧型SCF结构基于性能的抗震设计方法，给出了一幢3层自复位耗能节点框架结构的设计实例，通过有限元模拟对该结构的动力响应进行比较分析，得到以下结论：
(1)本文采用基于性能的设计方法，参考国内外规范对结构性能水平的量化值，确定了自复位耗能节点框架结构的抗震性能的位移指标；
(2)根据本文提出的基于性能的抗震设计方法设计的梁端弹簧型SCF结构，在多遇地震、设防地震及罕遇地震作用下结构的层间位移角均满足预设的结构性能目标，证明了该设计方法的有效性；
(3)通过实例计算分析表明，相比于常规框架结构，梁端弹簧型自复位耗能框架结构具有较小的加速度响应和剪力响应，以及可控的变形性能，体现了梁端弹簧型SCF结构优越的抗震性能。
-
![]()
图 4 基于性能设计的层间位移极限状态
Figure 4. Limit states of inter-story drift ratio based on performance design
![]()
图 6 框架结构平面布置图与计算单元选取 /mm
Figure 6. Layout and calculation unit selection of frame structure
![]()
图 9 El Centro-EW波作用下结构层间位移响应
Figure 9. Inter-story drifts of structures under El Centro-EW earthquake
![]()
图 10 El Centro-EW波作用下结构层间剪力
Figure 10. Inter-story shear forces of structures under El Centro-EW earthquake
![]()
图 11 El Centro-EW波作用下加速度响应
Figure 11. Acceleration response under El Centro-EW earthquake
表 1 FEMA356不同性能要求的层间位移角
Table 1 Inter-story drifts for different performance requirements in FEMA356
结构类型 立即使用(IO) 生命安全(LS) 防止倒塌(CP) 混凝土框架 1/100 1/50 1/25 钢框架 1/143 1/40 1/20 带斜撑钢框架 1/200 1/67 1/50 混凝土剪力墙 1/200 1/100 1/50 
下载: 导出CSV
表 2 GB 50011层间位移角限值
Table 2 Inter-story drift limits in Chinese seismic design code
结构类型 弹性变形 弹塑性变形 钢筋混凝土框架结构 1/550 1/50 钢筋混凝土框架-抗震墙、板柱-抗震墙、
框架-核心筒1/800 1/100 钢筋混凝土抗震墙、筒中筒 1/1000 1/100 钢筋混凝土框支层 1/1000 1/120 多、高层钢结构 1/250 1/50
下载: 导出CSV
表 3 水平向减震系数分档
Table 3 Horizontal damping coefficient grading
设防烈度(设计基本
地震加速度)水平向减震系数β 0.53≥β≥0.40 0.40>β>0.27 β≤0.27 9(0.40 g) 8(0.30 g) 8(0.20 g) 7(0.15 g) 8(0.30 g) 8(0.20 g) 7(0.15 g) 7(0.10 g) 8(0.20 g) 7(0.15 g) 7(0.10 g) 7(0.10 g) 7(0.15 g) 7(0.10 g) 7(0.10 g) 6(0.05 g) 7(0.10 g) 7(0.10 g) 6(0.05 g) 6(0.05 g)
下载: 导出CSV
表 4 钢板弹簧及金属阻尼器参数
Table 4 Parameters of leaf spring and metal damper
结构 钢板弹簧转动刚度/((kN·m)/rad) 阻尼器 梁柱中
节点梁柱边
节点柱脚
节点初始刚度/
(kN/mm)屈服力/
kN屈服位移/
mm有控结构 800 400 800 12.5 30 2.4 无控结构 800 400 800 − − −
下载: 导出CSV
表 5 地震波信息
Table 5 Information of seismic wave
地震波 震级 时间 PGA/gal 持续时间/s 场地 El Centro-EW 7.1 1940 210.1 54.38 Ⅱ Taft-NS 7.7 1957 152.7 53.38 Ⅲ SH09-1 — — — 40.00 Ⅳ
下载: 导出CSV
表 6 结构前3阶自振周期
Table 6 The first three natural vibration periods
结构类型 三阶自振周 T1/s T2/s T3/s 常规框架 0.3130 0.0964 0.0549 无控SCF 3.1027 0.2349 0.0747 有控SCF 1.6917 0.2108 0.0729
下载: 导出CSV
表 7 地震动下的位移响应
Table 7 Displacement responses under ground motions
峰值地面
加速度/g地震波 El Centro-EW Taft-NS SH09-1 楼层 F1/mm F2/mm F3/mm F1/mm F2/mm F3/mm F1/mm F2/mm F3/mm 0.07 常规框架 3.74 3.88 2.01 3.63 3.59 1.57 3.49 3.55 2.03 无控SCF 25.63 24.84 23.67 23.41 21.55 21.71 23.11 22.29 23.96 有控SCF 13.01 12.42 12.34 11.27 10.72 10.22 15.69 15.51 14.76 0.20 常规框架 10.10 6.90 2.50 12.60 10.89 4.10 10.10 11.80 6.20 无控SCF 64.21 61.72 61.33 50.16 49.68 49.61 65.66 67.39 65.86 有控SCF 35.71 34.54 34.24 30.10 28.38 27.67 46.89 47.92 46.04 0.40 常规框架 53.49 46.11 17.00 32.78 34.62 17.29 75.69 45.86 14.66 无控SCF 141.50 140.90 142.30 85.90 83.70 84.20 179.70 182.40 182.80 有控SCF 88.45 87.37 89.68 45.10 42.90 43.00 112.30 113.20 114.00
下载: 导出CSV
表 8 地震动下的层间剪力响应
Table 8 Inter-story shear responses under ground motions
峰值地面加速度/g 地震波 El Centro-EW Taft-NS SH09-1 楼层 F1/kN F2/kN F3/kN F1/kN F2/kN F3/kN F1/kN F2/kN F3/kN 0.07 常规框架 395.3 283.2 148.9 379.6 263.0 147.5 318.2 262.8 157.3 无控SCF 125.2 64.3 59.1 97.6 61.0 38.8 112.5 78.4 65.1 有控SCF 138.0 77.0 65.7 106.3 64.9 43.7 122.9 89.3 76.5 0.20 常规框架 855.2 519.9 296.1 710.9 430.8 253.7 740.7 476.8 264.1 无控SCF 289.6 176.4 119.7 263.4 172.0 114.2 276.8 206.2 152.5 有控SCF 277.8 172.8 115.2 250.8 164.7 105.6 267.9 198.5 145.7 0.40 常规框架 1078 814.8 488.6 944.1 765.9 466.4 814.5 641.9 481.6 无控SCF 458.3 307.7 176.4 419.3 305.0 152.6 431.6 345.1 289.3 有控SCF 398.6 281.4 163.9 390.3 286.4 129.6 410.5 322.7 250.7
下载: 导出CSV
表 9 地震动下的加速度响应K值
Table 9 Acceleration responses K under ground motions
响应参数 峰值地面加速度/g 地震波 El Centro-EW Taft-NS SH09-1 楼层 F1 F2 F3 F1 F2 F3 F1 F2 F3 加速度响应/(m∙s−2) 0.07 常规框架 1.82 2.02 2.39 1.76 2.05 2.53 1.51 1.92 2.47 无控SCF 1.02 0.73 1.22 1.19 0.65 1.12 1.28 0.96 1.47 有控SCF 1.08 0.82 1.25 1.28 0.77 1.30 1.33 1.05 1.58 0.20 常规框架 3.62 3.81 4.03 3.92 4.76 5.85 3.92 4.76 5.85 无控SCF 2.89 2.06 3.18 3.66 2.41 3.80 3.66 2.41 3.80 有控SCF 2.70 1.94 2.92 3.44 2.38 3.68 3.44 2.38 3.68 0.40 常规框架 5.80 8.39 9.56 5.73 6.93 8.59 5.21 6.95 7.21 无控SCF 4.91 3.50 3.98 6.82 4.55 6.73 6.92 4.88 6.90 有控SCF 4.75 3.09 4.41 6.77 4.34 6.78 6.42 4.43 6.75 动力放大系数K 0.07 常规框架 2.60 2.89 3.41 2.51 2.93 3.61 2.16 2.74 3.53 无控SCF 1.46 1.04 1.74 1.70 0.93 1.60 1.83 1.37 2.10 有控SCF 1.54 1.17 1.79 1.83 1.10 1.86 1.90 1.50 2.26 0.20 常规框架 1.81 1.91 2.02 1.96 2.38 2.93 1.96 2.38 2.93 无控SCF 1.45 1.03 1.59 1.83 1.21 1.90 1.83 1.21 1.90 有控SCF 1.35 0.97 1.46 1.72 1.19 1.84 1.72 1.19 1.84 0.40 常规框架 1.45 2.10 2.39 1.43 1.73 2.15 1.30 1.74 1.80 无控SCF 1.23 0.88 1.00 1.71 1.14 1.68 1.73 1.22 1.73 有控SCF 1.19 0.77 1.10 1.69 1.09 1.70 1.61 1.11 1.69
下载: 导出CSV
-
[1] PRIESTLEY M J N. Overview of PRESSS research program [J]. PCI Journal, 1991, 36(4): 50 − 57. doi: 10.15554/pcij.07011991.50.57
[2] PRIESTLEY M J N, TAO J R. Seismic response of precast prestressed concrete frames with partially debonded tendons [J]. PCI Journal, 1993, 38(1): 58 − 69. doi: 10.15554/pcij.01011993.58.69
[3] WOLSKI M, RICLES J M, SAUSE R. Experimental study of a self-centering beam–column connection with bottom flange friction device [J]. Journal of Structural Engineering, 2009, 135(5): 479 − 488. doi: 10.1061/(ASCE)ST.1943-541X.0000006
[4] CHOU C C, LAI Y J. Post-tensioned self-centering moment connections with beam bottom flange energy dissipators [J]. Journal of Constructional Steel Research, 2009, 65(10/11): 1931 − 1941.
[5] 吕西林, 崔晔, 刘兢兢. 自复位钢筋混凝土框架结构振动台试验研究 [J]. 建筑结构学报, 2014, 35(1): 19 − 26. LYU Xilin, CUI Ye, LIU Jingjing. Shaking table test of a self-centering reinforced concrete frame [J]. Journal of Building Structures, 2014, 35(1): 19 − 26. (in Chinese)
[6] 蔡小宁, 孟少平, 孙巍巍. 自复位预制框架边节点组件受力性能试验研究 [J]. 工程力学, 2014, 31(3): 160 − 167. doi: 10.6052/j.issn.1000-4750.2012.10.0764 CAI Xiaoning, MENG Shaoping, SUN Weiwei. Experimental study on performance of components of the exterior self-centering post-tensioned precast connections [J]. Engineering Mechanics, 2014, 31(3): 160 − 167. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.10.0764
[7] 鲁亮, 江乐, 李鸿, 等. 柱端铰型受控摇摆式钢筋混凝土框架抗震性能的振动台试验研究 [J]. 振动与冲击, 2016, 35(4): 193 − 198, 216. LU Liang, JIANG Le, LI Hong, et al. Shaking table tests for aseismic performance of a controllable rocking reinforced concrete frame with column-end-hinge joints [J]. Journal of Vibration and Shock, 2016, 35(4): 193 − 198, 216. (in Chinese)
[8] 鲁亮, 叶雨立, 夏婉秋, 等. 体外预应力自复位钢筋混凝土框架抗震性能振动台试验研究 [J]. 土木工程学报, 2020, 53(增刊2): 68 − 73, 108. LU Liang, YE Yuli, XIA Wanqiu, et al. Study on the seismic performance of a 3D external prestressed self-centering reinforced concrete frame by shaking table test [J]. China Civil Engineering Journal, 2020, 53(Suppl 2): 68 − 73, 108. (in Chinese)
[9] 鲁亮, 陈凯芳, 胡宇飞. 梁端弹簧自复位框架耗能节点试验研究 [J]. 结构工程师, 2019, 35(1): 122 − 130. LU Liang, CHEN Kaifang, HU Yufei. Experimental research on the energy-dissipating self-centering frame joint with beam-end spring [J]. Structural Engineers, 2019, 35(1): 122 − 130. (in Chinese)
[10] 鲁亮, 汪磊, 胡宇飞. 梁端弹簧型自复位耗能框架节点刚度取值研究 [J]. 动力学与控制学报, 2020, 18(5): 22 − 28. LU Liang, WANG Lei, HU Yufei. Selection of joint stiffness for an energy-dissipating self-centering frame joint with beam-end spring [J]. Journal of Dynamics and Control, 2020, 18(5): 22 − 28. (in Chinese)
[11] BERTERO V V. Major issue and future directions in earthquake-resistant design [C]// Proceedings of the 10th World Conference on Earthquake Engineering. Madrid, Spain: International Association for Earthquake Engineering, 1992: 6407 − 6444.
[12] 蒋欢军, 郑建波, 张桦. 基于位移的抗震设计研究进展[J]. [J]. 工业建筑, 2008, 38(7): 1 − 5, 15. JIANG Huanjun, ZHENG Jianbo, ZHANG Ye. State of the art of displacement-based seismic design [J]. Industrial Construction, 2008, 38(7): 1 − 5, 15. (in Chinese)
[13] 门进杰, 霍文武, 兰涛, 等. 基于刚度和位移带可更换构件RCS混合框架结构抗震设计方法 [J]. 工程力学, 2021, 38(4): 169 − 178. doi: 10.6052/j.issn.1000-4750.2020.06.0370 MEN Jinjie, HUO Wenwu, LAN Tao, et al. Seismic design method of RCS hybrid frame structure with replaceable members based on stiffness and displacement [J]. Engineering Mechanics, 2021, 38(4): 169 − 178. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0370
[14] 王玉奎, 刘哲锋, 张丹, 等. RC梁构件基于能量的抗震设计方法研究 [J]. 工程力学, 2023, 40(11): 218 − 226. doi: 10.6052/j.issn.1000-4750.2022.04.0278 WANG Yukui, LIU Zhefeng, ZHANG Dan, et al. Research on energy based seismic design method of RC beam members [J]. Engineering Mechanics, 2023, 40(11): 218 − 226. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.04.0278
[15] 门进杰, 史庆轩, 周琦. 框架结构基于性能的抗震设防目标和性能指标的量化 [J]. 土木工程学报, 2008, 41(9): 76 − 82. MEN Jinjie, SHI Qingxuan, ZHOU Qi. Performance-based seismic fortification criterion and quantified performance index for reinforced concrete frame structures [J]. China Civil Engineering Journal, 2008, 41(9): 76 − 82. (in Chinese)
[16] FEMA 356, Prestandard and commentary for the seismic rehabilitation of buildings [S]. Washington: Federal Emergency Management Agency, 2000.
[17] GB 50011−2010, 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2010. GB 50011−2010, Code for seismic design of building [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[18] 吴晓涵. NosaCAD与ABAQUS和PERFORM-3D弹塑性模型转换及分析应用 [J]. 建筑结构, 2012, 42(增刊 2): 207 − 212. WU Xiaohan. Model transformation from NosaCAD to ABAQUS and PERFORM-3D and nonlinear structure analysis by these software [J]. Building Structure, 2012, 42(Suppl 2): 207 − 212. (in Chinese)
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 118
- HTML全文浏览量: 44
- PDF下载量: 16
- 被引次数: 1
