钢筋与混凝土之间可靠的粘结是钢筋混凝土构件中钢筋与混凝土协调变形、共同承载的前提^{[1 − 2]}。随着结构服役时间的延长，钢筋混凝土结构以不同的形式和速度退化，最终降低结构承载力^{[3 − 4]}。与此同时，火灾等极端的环境将进一步加速钢筋及混凝土间可靠的粘结性能退化这一过程^{[5 − 6]}。因此，亟待深入研究锈蚀钢筋—混凝土结构高温粘结强度的预测方法，以全面了解锈蚀钢筋混凝土结构经受高温后的粘结行为，促进在实际工程环境中锈蚀钢筋混凝土结构的优化使用。

近年来，锈蚀对粘结性能影响的研究较为成熟。这些研究覆盖了粘结机理^{[7 − 8]}、粘结强度^{[9 − 10]}、影响粘结的主要因素^{[11 − 12]}等方面内容，取得了大量的成果。然而，这些研究是在常温下得到的，忽略了温度变化的影响，而高温会加剧RC构件中材料性能的退化。尽管也在高温作用下开展了一系列拉拔试验，研究高温下钢筋和混凝土之间的粘结性能^{[13 − 16]}。但均以未锈蚀钢筋为基础，而忽略了钢筋锈蚀后将会增强粘结界面的膨胀应力，引起混凝土锈胀开裂，甚至造成保护层胀裂，其耐火性能也存在着较大差距。在此基础上，众学者进行了诸多高温作用下锈蚀钢筋与混凝土间粘结性能研究，得到高温锈蚀等变量相关的粘结强度关系^{[17 − 26]}。然而，基于实验方法得出粘结强度表达式的计算精度仍然有限，因为粘结强度预测问题是一个涉及多变量的高维问题，实验方法无法充分考虑到高温锈蚀和材料参数等影响因素之间的多变量相关性。此外，这些经验模型都是基于有限的实验数据拟合的，对自身拟合试验数据有较高的敏感性。

得益于机器学习(ML)的发展，基于数据驱动的钢筋-混凝土粘结强度预测方法为解决上述难题提供了新的思路^{[27 − 28]}。机器学习等方法可充分利用历史试验数据，挖掘试验数据中输入与输出之间的映射关系，从而建立起精确、稳定的预测模型。DAHOU等^[29]提出了一种人工神经网络(ANN)模型来预测带肋钢筋与混凝土之间的粘结性能。结果表明：该模型具有较好的预测能力和泛化能力。GOLAFSHANI等^[30]建立了钢筋混凝土粘结强度的人工神经网络和模糊逻辑(FL)模型。结果表明：该模型可以在较短的时间内进行预测，且误差可以接受。LI等^[31]采用九种机器学习方法来预测超高性能混凝土(UHPC)与钢筋之间的粘结强度。结果表明：人工神经网络和随机森林的预测性能都很好，远远超过经验公式。CAVALERI等^[32]提出了一种基于卷积的集成学习模型来预测锈蚀钢筋混凝土界面粘结强度。结果表明：模型具有良好的预测效果。CONCHA^[33]基于现有的184个试验数据，建立了FRP筋混凝土粘结强度人工神经网络(ANN)预测模型。结果表明：N7-10-1模型与实验结果拟合良好。HUANG等^[34]利用文献中151组拉拔试验数据，建立了FRP筋混凝土在高温下的BP-ANN模型。结果表明：该模型比现有的数学模型具有更大的通用性。MEI等^[35]基于自然梯度增强(NGBoost)算法，建立了高温下钢筋与混凝土粘结强度的统一概率预测模型。结果表明：该模型比经验公式具有更高的精度。

迄今为止，尚未对机器学习方法在预测锈蚀钢筋-混凝土高温粘结强度方面进行明确的探究。考虑到多变量因素，研究机器学习方法是否可用于预测锈蚀钢筋混凝土高温粘结强度是至关重要的。此外，大多数ML方法都存在“黑盒”现象，模型应用于工程实践有局限性。因此，迫切需要提供一种可解释的ML方法来填补锈蚀钢筋混凝土高温粘结强度模型在实用性和可解释性方面的空白。

本文提出了一种基于机器学习技术的锈蚀钢筋混凝土高温粘结强度预测的智能方法。该模型以机器学习算法ANN与XGB模型为基础，基于以往的锈蚀钢筋混凝土高温粘结强度的612组试验研究数据，以温度、锈蚀率、钢筋直径、粘结长度、混凝土保护层厚度、混凝土抗压强度、钢筋屈服强度为输入变量，界面粘结强度为输出目标，构建了粘结性能影响因素与粘结强度之间的关系，探讨了ANN与XGB算法对粘结强度的预测效果。此外，为了清楚地分析输入特征对最终结果的影响，该模型使用SHAP方法来评估输入特征和输出结果之间的关系，分析输入参数的重要性，以克服机器学习方法的“黑盒子”问题。同时，将ANN与XGB模型与经验模型进行了比较，进一步验证ANN与XGB模型在锈蚀钢筋混凝土高温粘结强度预测中的有效性和通用性。

1   试验数据库

1.1   数据库建设

本文通过对各种锈蚀钢筋混凝土高温粘结性能试验数据^{[17 − 26]}的汇总，建立了一个新的机器学习模型实验数据库，共612个实验数据样本。数据库中记录的输入输出特征值和数据汇总见表1。数据库中记录了影响粘结强度的主要因素。图1和表1显示了输入和输出参数的分布。其中考虑了7个有效特征作为输入变量，包括温度、锈蚀率、钢筋直径、粘结长度、混凝土保护层厚度、混凝土抗压强度、钢筋屈服强度。更具体地说，温度(T)、锈蚀率(η)、钢筋直径(d)、粘结长度(L)、混凝土保护层厚度(c)、混凝土抗压强度(f_c)、钢筋屈服强度(f_y)的范围分别为20 ℃~800 ℃、0.00%~10.73%、8 mm~20 mm、40 mm~100 mm、20 mm~90 mm、6.97 MPa~57.00 MPa、312.64 MPa~558.00 MPa。输出变量为粘结强度(τ_u)，范围为0.51 MPa~35.94 MPa。这保证了数据库的可靠性和代表性，有利于ML模型评估粘结强度的可预测性。

表  1  数据库输入输出变量信息统计表

Table  1.  Input and output parameters statistics

分类	变量	数据
		最小值	最大值	平均值	偏差
输入	T/(℃)	20.00	800.00	323.80	256.01
输入	η/(%)	0.00	10.73	2.46	2.54
输入	d/mm	8.00	20.00	17.11	3.48
输入	L/mm	40.00	100.00	63.61	22.84
输入	c/mm	20.00	90.00	47.96	14.62
输入	fc/MPa	6.97	57.00	32.55	13.45
输入	fy/MPa	312.64	558.00	488.85	57.05
输出	τu/MPa	0.51	35.94	11.78	8.17

下载: 导出CSV 

| 显示表格

图  1  粘结强度与输入特征参数关系

Figure  1.  Scatter graphs of input and output parameters distributions

下载: 全尺寸图片 幻灯片

1.2   基于数据库的粘结强度参数敏感性分析

基于组分含量分布图，我们对所收集的数据库进行了进一步的分析，并绘制了各参数之间的Pearson相关系数矩阵图，以更好地理解参数敏感性。如图2所示。如果输入变量之间的相关系数正负值过高，可能会导致效率较低，难以确定这些变量对结果的影响。从总体上来看，输入变量间的相关系数变化范围在[−0.57 ∶0.43]之间，独立的输入变量之间没有显著的相关性。此外，输入输出变量之间的相关性也较弱，变化范围在[−0.46∶0.49]之间。这意味着所有的变量都可以用来构建ML模型。

图  2  单一特征参数间的皮尔逊相关系数矩阵图

Figure  2.  Pearson correlation matrix plot between variables

下载: 全尺寸图片 幻灯片

2   机器学习算法

由于粘结强度不同影响因素之间存在复杂的相关性，选择了2种具有代表性的机器学习算法，分别从单一和集成机器学习算法角度进行粘结强度预测。主要包括人工神经网络(ANN)和极端梯度提升树(XGB)。

1)人工神经网络

人工神经网络是一种模拟生物神经元进行学习的智能数据处理技术，由连接的节点或单元的集合组成。通常由输入层、隐藏层和输出层三部分组成。“隐藏层”是ANN的核心，由许多神经元组成。在每个神经元内部，对输入变量进行运算得出输出变量并通过可修改的加权互连彼此连接。模型的主要参数为隐藏层数量和该层神经元的节点数量。本研究通过将隐藏层的数目设置为8，该层神经元的节点数量设置为16，所有其他参数默认，构建了ANN模型。隐藏层中神经元i的输出可以表示为式(1)^{[36 − 37]}：

式中：${x_i}(i = 1,2,3, \cdot \cdot \cdot ,n)$为第i个神经元的输入值；${w_{ij}}$为从第i个神经元到第j个神经元的连接权值；b为这个神经元的阈值；F为激活函数；y为该人工神经元的输出。

激活函数采用双曲正切S形函数，该函数的输出范围为−1~1，具体表达式见(2)：

2)极端梯度提升树

XGB是一种新建立的boosting类集成学习模型的典型机器学习算法^[38]，有助于避免过拟合以及优化计算能力。这是通过最小化目标函数来实现的。此外，在梯度提升树的基础上增加了正则化项，同时保持尽可能最快的处理速度。本研究通过将决策树的数目设置为200，学习速率设置为0.1，所有其他参数默认，构建了XGB模型。XGB算法的预测可以根据式(3)~式(4)来实现^{[39 − 40]}。XGB算法的目标是使预测${\hat y _i}$接近真值${y_i}$，经过m次迭代，目标函数L可以表示为：

式中：$l\left( {{y_i},\hat y _i^{m - 1}} \right)$为用于评估$\hat y _i^{m - 1}$精度的损失函数；${f_m}({x_i})$为回归树的预测值；$\varOmega \left( {{f_m}} \right)$为正则化项；C为常数值。采用二阶泰勒展开后，式(4)可简化为：

式中，${g_i}{\text{ = }}{l'}\left( {{y_i},\hat y _i^{m - 1}} \right)$和${h_i}{\text{ = }}{l''}\left( {{y_i},\hat y _i^{m - 1}} \right)$。

3   模型运行与结果分析

3.1   模型训练及测试流程

本节解释了用于预测锈蚀钢筋混凝土高温粘结强度的机器学习模型的构建方法。该方法的框架分为6个阶段：数据收集、数据处理、模型训练、获取模型最优参数、模型验证和模型解释。

第1步-数据收集：将已有文献中锈蚀钢筋混凝土高温粘结性能实验研究的数据进行汇总，用于训练和测试机器学习模型。

第2步-数据处理：对输入样本和输出样本数据进行预处理，进行数据归一化和分区。将数据归一化到[0,1]范围。然后，将612组数据随机分成两个数据集。其中选择489组数据(80%)作为训练集，选择123组数据(20%)作为测试集。

第3步-模型训练：利用训练数据集训练ANN和XGB模型；采用评价指标来评估ML模型的预测稳定性。

第4步-获取模型最优参数：经过多次编程测试，获得各个模型主要参数的最优超参数。

第5步-模型验证：使用测试数据集来评估模型的性能，根据获得的R²、RMSE、MAPE、MAE和a20−index值，进行模型进一步的分析和讨论。

第6步-模型解释：结合SHAP方法，对模型从全局和局部的角度对预测结果进行了解释。

3.2   评价指标

为了评估机器学习模型的性能，本研究采用以下五个指标：R²、RMSE、MAE、MAPE和a20−index，具体定义如表2所示。

表  2  评价指标

Table  2.  Statistical indicators

指标	公式	理想值
R2	${{{R}}^{\text{2}}}{\text{ = }}\dfrac{{\displaystyle\sum\nolimits_{i = 1}^n {{{\left( {{x_i} - {p_i}} \right)}^2} - \displaystyle\sum\nolimits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} } }}{{\displaystyle\sum\nolimits_{i = 1}^n {{{\left( {{x_i} - {\mu _i}} \right)}^2}} }}$	1
RMSE	${{{\rm RMSE} = }}\sqrt {\dfrac{1}{n}\displaystyle\sum\nolimits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} }$	0
MAE	${{{\rm MAE} = }}\dfrac{1}{n}\displaystyle\sum\nolimits_{i = 1}^n {\left| {{x_i} - {y_i}} \right|}$	0
MAPE	${{{\rm MAPE} = }}\dfrac{1}{n}\displaystyle\sum\nolimits_{i = 1}^n {\left| {\dfrac{{{x_i} - {y_i}}}{{{x_i}}}} \right|} \times 100\text{%}$	0
a20−index	${{a{{\rm 20-index}} = }}\dfrac{{m{\rm 2}0}}{n}$	1
注：xi为实际值；yi为预测值；pi为实际值的平均值；${\mu _i}$为预测值的平均值；n为数据集的样本总数；m20为实验值与预测值的比值在0.80~1.20的样本数。

下载: 导出CSV 

| 显示表格

3.3   模型预测性能及验证分析

表3给出了使用训练数据集和测试数据集得到的基于ANN和XGB模型的R²、RMSE、MAE、MAPE和a20-index。从表3中可以进一步观察到，XGB算法的训练集R²达到了0.9832，明显高于ANN算法的0.9450，提高了超过4.04%。XGB算法的训练集a20-index达到了0.9346，明显高于ANN算法的0.7505，提高了超过24.53%。这表明XGB对样本的拟合性能更为良好。此外，与ANN相比，XGB的RMSE减少了超过77.58%，MAE减少了超过7.79%，显示它们的预测值与实际值之间的差异最小，预测准确性明显优于ANN。对于测试数据集，ANN和XGB模型的R²值分别为0.9180和0.9421，a20-index值分别为0.7073和0.7398。结果进一步证实，在两个模型中，XGB模型表现出更好的预测能力。

表  3  所开发机器学习模型的性能评价指标

Table  3.  Statistical evaluation of the multiple models developed

数据集	模型	R2	RMSE	MAE	MAPE	a20-index
训练集	ANN	0.9450	1.8867	1.3230	0.2049	0.7505
	XGB	0.9832	1.0624	0.6367	0.0777	0.9346
测试集	ANN	0.9180	2.3758	1.7399	0.2468	0.7073
	XGB	0.9421	1.9115	1.3060	0.1959	0.7398

下载: 导出CSV 

| 显示表格

图3展示了两个模型的回归预测结果的散点图。如图3所示，与ANN相比，基于XGB的高温粘结强度的预测值更集中在±20%的误差限内，其在这一范围内的比例显著更高。这表明基于XGB算法的CRC高温粘结强度的预测模型在样本中表现更为良好。

图  3  机器学习模型预测拟合结果

Figure  3.  Fitting result of bond strength for ML models

下载: 全尺寸图片 幻灯片

图4展示了使用两种机器学习算法(ANN和XGB)对锈蚀钢筋混凝土高温粘结强度预测模型的预测值与实验值的比较。从图4中可以直观看出，模型的预测值与实测结果很好地一致。在统计学上，R²值越接近1，相应的误差测量就越低，表示模型性能越好。从工程角度来看，a20-index值越接近1，模型的预测性就越好。通过比较表3和图4，我们可以观察到集成模型XGB在预测方面优于单一的ANN模型。结果进一步证实了XGB模型具有更为良好的预测能力。

图  4  机器学习模型预测比较试验结果

Figure  4.  Comparison between actual and predicted results from ML models

下载: 全尺寸图片 幻灯片

3.4   模型解释

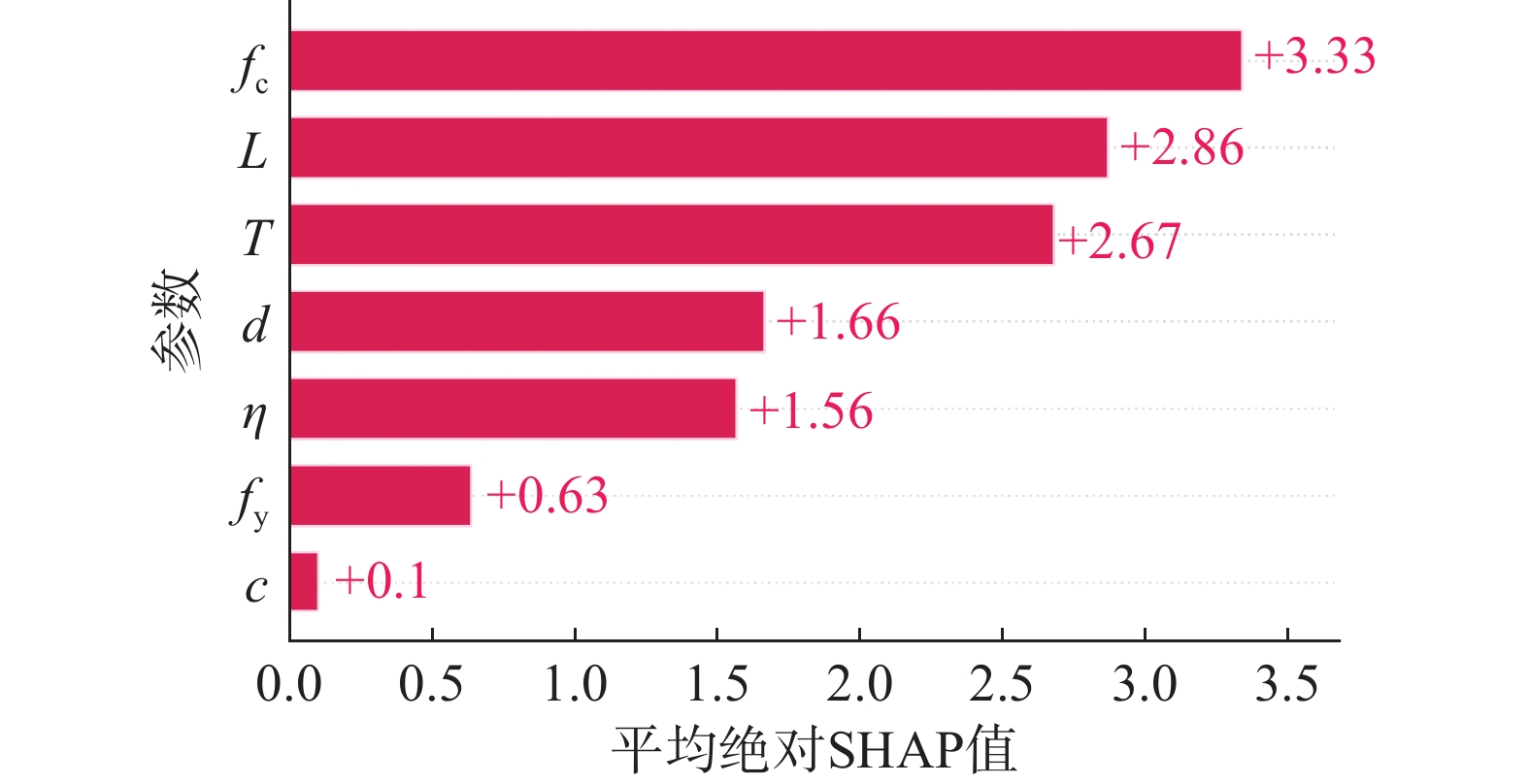
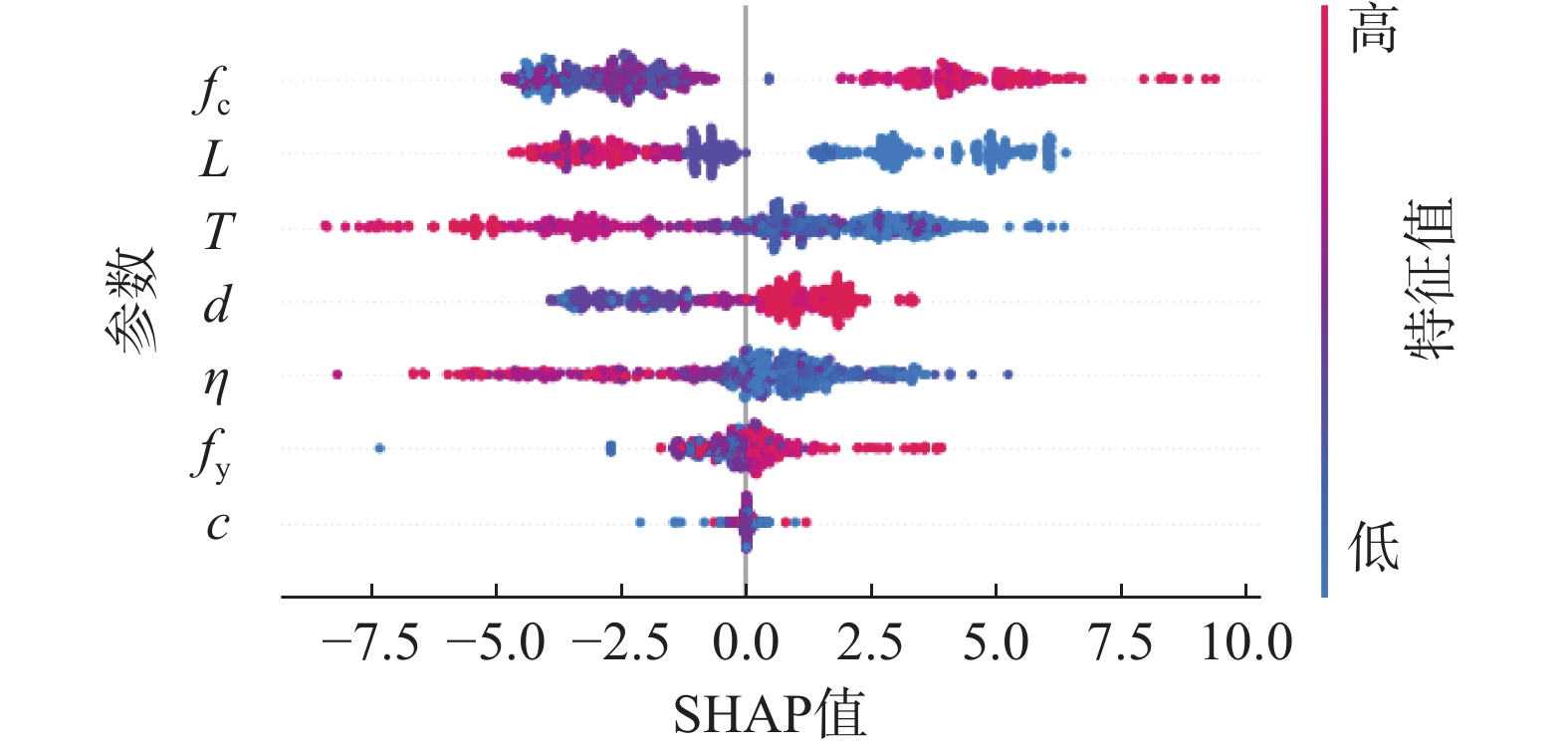
本研究采用SHAP方法对模型预测结果进行解释。根据所建立的模型，基于Shapley值的预测结果贡献分析可以分为两个层次。图5和图6给出了XGB模型全局层面的解释。结果表明：f_c对高温锈蚀钢筋混凝土粘结性能的影响最为显著，而c对粘结性能的影响最小。此外，图6展示了每个特征参数的SHAP值的分布，并示意了相应的影响趋势。其中，f_c、d、f_y越大，SHAP值越大；L、T、η越大，SHAP值越小。这表明，f_c、d、f_y与粘结强度呈正相关，而L、T、η则是负相关。图7为每个个体样本提供了局部解释。基准值为所建立的XGB模型对整个数据库预测的平均值，为11.72 MPa。如图7所示的可视化结果表明，样本预测结果为8.55 MPa。其中，f_c、d均对结果存在有利影响，η、T和L均对粘结强度有不利影响。这进一步说明机器学习方法对于锈蚀钢筋混凝土高温粘结强度预测的可靠性。

图  5  特征重要性图

Figure  5.  Feature importance of variables in SHAP

下载: 全尺寸图片 幻灯片

图  6  总和评估图

Figure  6.  SHAP summary chart for seven input variables

下载: 全尺寸图片 幻灯片

图  7  单样本解释图

Figure  7.  Graph of the SHAP prediction interpretation for a single sample

下载: 全尺寸图片 幻灯片

4   模型比较分析

为了确定所研究算法方法的有效性，将ANN和XGB模型与前人^{[17, 19, 22]}提出的三个经验公式计算的结果进行比较。

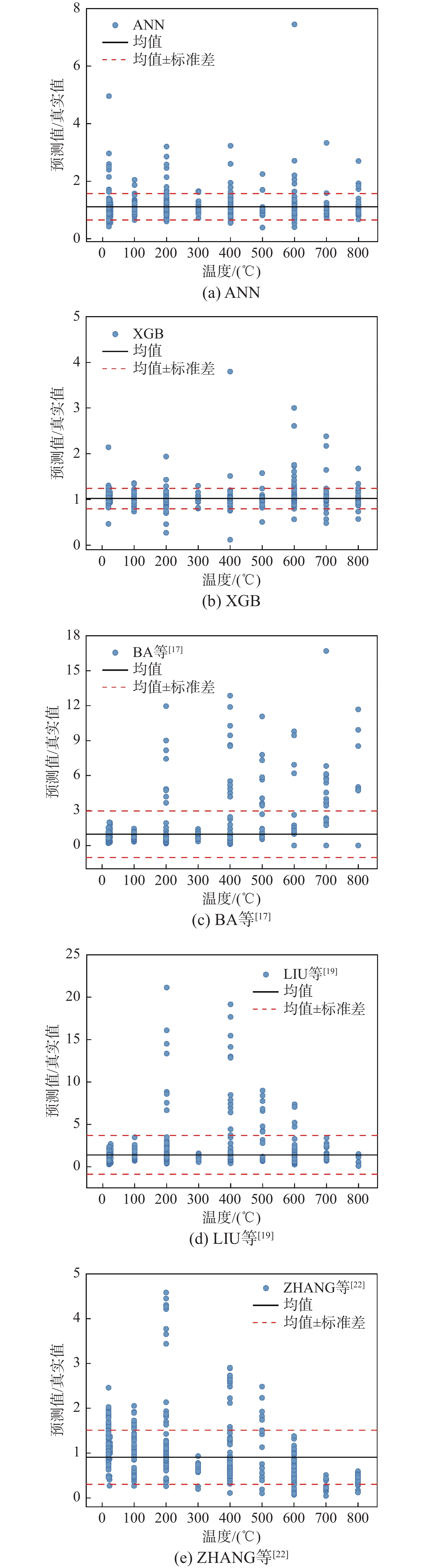
表4呈现了三个经验模型和ANN、XGB模型的预测粘结强度与实际粘结强度比值的比较结果，包括均值、标准差和变异系数。通过图8展示了计算与真实比值随温度变化的趋势。从表4和图8可以观察到，ANN和XGB模型的计算与实验比值的变异系数分别为21.96%和41.42%，远远小于经验模型的205.48%、163.33%和66.56%。这表明本研究提出的模型具有高计算精度和低变异性。表5呈现了三个经验模型和ANN、XGB模型的R²、RMSE、MAE和MAPE的比较结果。从表5中可以进一步观察到，ANN和XGB模型的R²值分别为0.9754和0.9400，表明其与样本拟合良好。在三个经验公式中，由ZHANG等^[22]提出的模型表现更为良好。然而，该经验模型的R²仅为0.5739，远小于XGB和ANN模型的R²。此外，与经验模型^[22]相比，XGB和ANN模型的RMSE分别减少了3.12倍和1.64倍，MAE分别减少了3.94倍和1.71倍。该经验模型的MAPE为0.4304，比XGB模型(0.1014)高出四倍以上，比ANN模型(0.2133)高出两倍以上。因此，明显可见，本研究提出的机器学习模型在预测性能方面优于现有的理论计算公式。

表  4  不同模型对τ_e/τ_u 的评估

Table  4.  Evaluation of different models for the τ_e/τ_u

模型	最大值	最小值	平均值	偏差	变异系数
XGB	3.7988	0.4600	1.0214	0.2243	21.96
ANN	7.4508	0.3884	1.1118	0.4605	41.42
BA等[17]	16.6939	0.1104	0.9706	1.9944	205.48
LIU等[19]	21.1354	0.0753	1.3989	2.2848	163.33
ZHANG等[22]	4.5840	0.0453	0.9087	0.6048	66.56

下载: 导出CSV 

| 显示表格

图  8  模型计算值与实验值之比随温度变化情况

Figure  8.  Variation of the ratio of calculated to experimental values for each model with temperature

下载: 全尺寸图片 幻灯片

表  5  不同模型的性能评估指标

Table  5.  Performance evaluation metrics of different models

模型	R2	RMSE	MAE	MAPE
XGB	0.9754	1.2792	0.7712	0.1014
ANN	0.9400	1.9947	1.4068	0.2133
BA等[17]	−0.4242	10.7847	8.4400	1.0772
LIU等[19]	0.0032	8.1474	6.0621	0.9404
ZHANG等[22]	0.5739	5.2683	3.8074	0.4304

下载: 导出CSV 

| 显示表格

5   结论

本文提出了一种基于SHAP值的混合机器学习算法的锈蚀钢筋混凝土高温粘结强度预测模型，旨在利用机器学习算法(ANN和XGB)，根据给定的输入参数，合理预测锈蚀钢筋混凝土高温粘结强度。可以得出以下几个重要结论：

(1)利用数据库训练机器学习算法，建立了锈蚀钢筋混凝土高温粘结强度智能预测模型。结果表明，建立的2个ML模型均表现良好，总体而言，集成模型(XGB)的表现优于单一模型(ANN)，表现出更加良好的准确性。

(2)基于SHAP方法对模型从全局和局部的角度对预测结果进行了解释。结果表明，混凝土抗压强度、粘结长度、温度是影响锈蚀钢筋混凝土高温粘结强度最关键的参数。其中，f_c、d和f_y在一定范围内均对结果存在有利影响。相反，L、T、η对粘结强度有不利影响。

(3)比较了三个传统经验公式与ANN和XGB算法的预测结果。结果表明：经验公式的准确性有限，且变异性较大。相反，与传统的经验公式相比，ML模型大大提高了预测精度。ANN模型预测值与实际值比的变异系数为41.42%，XGB模型为21.96%，而经验模型的变异超过66%。