平面曲梁面外自由振动有限元分析的<i>p</i>型超收敛算法

叶康生; 梁童

doi:10.6052/j.issn.1000-4750.2019.11.0694

平面曲梁面外自由振动有限元分析的p型超收敛算法

叶康生^,,
梁童

清华大学土木工程系，土木工程安全与耐久教育部重点实验室，北京 100084

基金项目: 国家自然科学基金项目(51078198)；清华大学自主科研计划项目(2011THZ03)

详细信息

作者简介:
梁　童(1994−)，男，山东人，硕士生，主要从事结构工程研究(E-mail: liangt17@mails.tsinghua.edu.cn)

通讯作者:
叶康生(1972−)，男，江苏人，副教授，博士，主要从事结构工程研究(E-mail: yeks@tsinghua.edu.cn)

中图分类号: TU311.3
计量
- 文章访问数: 622
- HTML全文浏览量: 149
- PDF下载量: 86
出版历程
- 收稿日期: 2019-11-24
- 修回日期: 2020-03-04
- 网络出版日期: 2020-05-24
- 刊出日期: 2020-10-09

A p-TYPE SUPERCONVERGENT RECOVERY METHOD FOR FINITE ELEMENT ANALYSIS OF OUT-OF-PLANE FREE VIBRATIONS OF PLANAR CURVED BEAMS

YE Kang-sheng^,,
LIANG Tong

Department of Civil Engineering, Tsinghua University,Key Laboratory of Civil Engineering Safety and Durability of China Education Ministry, Beijing 100084, China

摘要

摘要: 该文用p型超收敛算法对平面曲梁面外自由振动问题进行求解。该法基于频率和振型结点位移在有限元解答中的超收敛特性，在单元上建立振型近似满足的线性常微分方程边值问题，用更高次元对该线性边值问题进行有限元求解获得各单元上振型的超收敛解，将振型的超收敛解代入Rayleigh商，得到频率的超收敛解。该法作为后处理法，修复计算分别在各个单元上单独进行，故通过少量计算即能显著提高频率和振型的精度和收敛阶。数值算例显示该法稳定、高效，值得进一步研究和推广。
- 平面曲梁 /
- 面外自由振动 /
- 有限元 /
- p型超收敛 /
- Rayleigh商
Abstract: It extends the p-type superconvergence recovery method to the finite element analysis of the out-of-plane free vibrations of planar curved beams. Based on the superconvergence properties on frequencies and nodal displacements in modes, a linear ordinary differential boundary value problem (BVP) which approximately governs the mode on each element is set up. This linear BVP is solved by using a higher order element from which the mode on each element is recovered. By substituting the recovered mode into the Rayleigh quotient, the frequency is recovered. This method is a post-processing approach. Its recovery computation for each element is handled only on its own domain. It can enhance the accuracy and convergence rate of the frequencies and modes significantly with a small computation cost. Numerical examples demonstrate that the method is stable, efficient and worth further exploring.
- planar curved beam /
- out-of-plane free vibration /
- finite element method /
- p-type superconvergence /
- Rayleigh quotient

HTML全文

图 1 平面曲梁

Figure 1. Planar curved beam

下载: 全尺寸图片幻灯片

图 2 有限元网格划分

Figure 2. Finite element mesh

下载: 全尺寸图片幻灯片

图 3 例1常截面圆弧曲梁

Figure 3. Uniform arch beam in Example 1

下载: 全尺寸图片幻灯片

图 4 例1第三阶频率、振型和结点位移的收敛阶

Figure 4. Rate of convergence of 3rd frequence, mode and its nodal displacement in Example 1

下载: 全尺寸图片幻灯片

图 5 例1第三阶振型的有限元解与超收敛解比较

Figure 5. Comparison of FE solution with recovered solution on 3rd mode in Example 1

下载: 全尺寸图片幻灯片

图 6 例1第三阶特征对有限元解与超收敛解收敛阶

Figure 6. Rate of convergence of FE solution and recovered solutions on 3rd eigenpair in Example 1

下载: 全尺寸图片幻灯片

图 7 例2常截面圆弧曲梁

Figure 7. Uniform arch beam in Example 2

下载: 全尺寸图片幻灯片

图 8 例2第26阶特征对有限元解与超收敛解收敛阶

Figure 8. Rate of convergence of FE solution and recovered solutions on 26th eigenpair in Example 2

下载: 全尺寸图片幻灯片

图 9 三类轴线曲梁

Figure 9. Three types of curved beams

下载: 全尺寸图片幻灯片

表 1 例1第三阶频率、振型和结点位移的收敛阶

Table 1 Rate of convergence of 3rd frequency, mode and its nodal displacement in Example 1

ne	$\|\varOmega {\rm{ - }}{\varOmega ^h}\|$	r	$\|\|{{{d}}_c}{\rm{ - }}{{d}}_c^h\|\|$	r	$\|\|{{d}}{\rm{ - }}{{{d}}^h}\|\|$	r
16	2.8821×10⁻³	−	7.5917×10⁻⁶	−	4.9237×10⁻⁴	−
32	1.8948×10⁻⁴	3.9	5.7596×10⁻⁷	3.7	6.2308×10⁻⁵	3.0
64	1.1998×10⁻⁵	4.0	3.7692×10⁻⁸	3.9	7.8069×10⁻⁶	3.0
128	7.5231×10⁻⁷	4.0	2.3827×10⁻⁹	4.0	9.7640×10⁻⁷	3.0
256	4.7058×10⁻⁸	4.0	1.4934×10⁻¹⁰	4.0	1.2207×10⁻⁷	3.0
512	2.9417×10⁻⁹	4.0	9.3404×10⁻¹²	4.0	1.5259×10⁻⁸	3.0
m=2		4		4		3

ne	$\|\varOmega {\rm{ - }}{\varOmega ^h}\|$	r	$\|\|{{{d}}_c}{\rm{ - }}{{d}}_c^h\|\|$	r	$\|\|{{d}}{\rm{ - }}{{{d}}^h}\|\|$	r
16	3.2911×10⁻⁶	−	2.0671×10⁻⁷	−	1.3848×10⁻⁵	−
32	5.2669×10⁻⁸	6.0	3.3117×10⁻⁹	6.0	8.1494×10⁻⁷	4.1
64	8.2793×10⁻¹⁰	6.0	5.2071×10⁻¹¹	6.0	5.0101×10⁻⁸	4.0
128	1.2956×10⁻¹¹	6.0	8.1489×10⁻¹³	6.0	3.1181×10⁻⁹	4.0
256	2.0251×10⁻¹³	6.0	1.2738×10⁻¹⁴	6.0	1.9468×10⁻¹⁰	4.0
512	3.1645×10⁻¹⁵	6.0	1.9905×10⁻¹⁶	6.0	1.2164×10⁻¹¹	4.0
m=3		6		6		4

ne	$\|\varOmega {\rm{ - }}{\varOmega ^h}\|$	r	$\|\|{{{d}}_c}{\rm{ - }}{{d}}_c^h\|\|$	r	$\|\|{{d}}{\rm{ - }}{{{d}}^h}\|\|$	r
16	2.0402×10⁻⁹	−	1.2643×10⁻¹⁰	−	2.3812×10⁻⁷	−
32	8.0841×10⁻¹²	8.0	4.9957×10⁻¹³	8.0	7.3852×10⁻⁹	5.0
64	3.1692×10⁻¹⁴	8.0	1.9571×10⁻¹⁵	8.0	2.3031×10⁻¹⁰	5.0
128	1.2390×10⁻¹⁶	8.0	7.6504×10⁻¹⁸	8.0	7.1933×10⁻¹²	5.0
256	4.8646×10⁻¹⁹	8.0	2.9890×10⁻²⁰	8.0	2.2476×10⁻¹³	5.0
512	1.8912×10⁻²¹	8.0	1.1676×10⁻²²	8.0	7.0236×10⁻¹⁵	5.0
m=4		8		8		5

下载: 导出CSV

表 2 例1第三阶特征对有限元解与超收敛解收敛阶

Table 2 Rate of convergence of FE solution and recovered solutions on 3rd eigenpair in Example 1

$m = 2$
$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^h}\|$	$r$	$\|\|{{d}} - {{{d}}^h}\|\|$	$r$
16	2.8821×10⁻³	−	4.9237×10⁻⁴	−
32	1.8948×10⁻⁴	3.9	6.2308×10⁻⁵	3.0
64	1.1998×10⁻⁵	4.0	7.8069×10⁻⁶	3.0
128	7.5231×10⁻⁷	4.0	9.7640×10⁻⁷	3.0
256	4.7058×10⁻⁸	4.0	1.2207×10⁻⁷	3.0
512	2.9417×10⁻⁹	4.0	1.5259×10⁻⁸	3.0
理论值		4		3

$\bar m = 3$
$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$r$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$r$
16	4.1065×10⁻⁵	−	1.4864×10⁻⁴	−
32	2.5175×10⁻⁷	7.3	9.6899×10⁻⁶	3.9
64	1.6723×10⁻⁹	7.2	6.1437×10⁻⁷	4.0
128	1.6325×10⁻¹¹	6.7	3.8746×10⁻⁸	4.0
256	2.1574×10⁻¹³	6.2	2.4284×10⁻⁹	4.0
512	3.2163×10⁻¹⁵	6.1	1.5188×10⁻¹⁰	4.0
理论值		6		4

$\bar m = 4$
$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$r$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$r$
16	3.7774×10⁻⁵	−	1.4864×10⁻⁴	−
32	1.9909×10⁻⁷	7.6	9.6899×10⁻⁶	3.9
64	8.4441×10⁻¹⁰	7.9	6.1233×10⁻⁷	4.0
128	3.3689×10⁻¹²	8.0	3.8378×10⁻⁸	4.0
256	1.3230×10⁻¹⁴	8.0	2.4003×10⁻⁹	4.0
512	5.1747×10⁻¹⁷	8.0	1.5004×10⁻¹⁰	4.0
理论值		8		4

$\bar m = 5$
$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$r$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$r$
16	3.7772×10⁻⁵	−	1.4864×10⁻⁴	−
32	1.9908×10⁻⁷	7.6	9.6899×10⁻⁶	3.9
64	8.4438×10⁻¹⁰	7.9	6.1233×10⁻⁷	4.0
128	3.3687×10⁻¹²	8.0	3.8378×10⁻⁸	4.0
256	1.3229×10⁻¹⁴	8.0	2.4003×10⁻⁹	4.0
512	5.1745×10⁻¹⁷	8.0	1.5004×10⁻¹⁰	4.0
理论值		8		4

下载: 导出CSV

表 3 例1第三阶特征对SPRD法收敛阶

Table 3 Rate of convergence of recovered solutions on 3rd eigenpair in Example 1 with SPRD method

$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$r$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$r$
32	1.9168×10⁻⁵	−	6.1793×10⁻⁵	−
64	2.6890×10⁻⁷	6.2	3.9614×10⁻⁶	4.0
128	3.9339×10⁻⁹	6.1	2.4915×10⁻⁷	4.0
256	5.9333×10⁻¹¹	6.1	1.5596×10⁻⁸	4.0
512	9.1038×10⁻¹³	6.0	9.7516×10⁻¹⁰	4.0
1024	1.4094×10⁻¹⁴	6.0	6.0954×10⁻¹¹	4.0

下载: 导出CSV

表 4 例2前12阶特征对有限元解与超收敛解误差

Table 4 Errors of FE solution and recovered solutions on first 12 eigenpairs in Example 2

阶数	$\varOmega$	${\varOmega ^h}$	$\|\varOmega - {\varOmega ^h}\|$	$\|\|{{d}} - {{{d}}^h}\|\|$	${\varOmega ^{\rm{*}}}$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$\dfrac{{\|\varOmega - {\varOmega ^{\rm{*}}}\|}}{{\|\varOmega - {\varOmega ^h}\|}}/( \text{%})$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$\dfrac{{\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|}}{{\|\|{{d}} - {{{d}}^h}\|\|}}/( \text{%})$	n
1	0.000000000	0.278903246	2.79×10⁻¹	1.21×10⁻³	0.003516615	3.52×10⁻³	1.26	8.75×10⁻⁶	0.72	1
2	2.096810333	2.379666689	2.83×10⁻¹	4.89×10⁻³	2.097006671	1.96×10⁻⁴	0.07	2.11×10⁻⁴	4.32	2
3	6.316663854	6.817878189	5.01×10⁻¹	1.11×10⁻²	6.317460674	7.97×10⁻⁴	0.16	9.77×10⁻⁴	8.76	3
4	12.156595065	13.009811658	8.53×10⁻¹	1.95×10⁻²	12.159147906	2.55×10⁻³	0.30	2.62×10⁻³	13.41	4
5	17.335703469	17.337172055	1.47×10⁻³	1.20×10⁻³	17.335703469	0.00×10⁰	0.00	7.65×10⁻⁶	0.64	1
6	19.209142151	20.568557976	1.36×10⁰	3.09×10⁻²	19.216004983	6.86×10⁻³	0.50	5.86×10⁻³	18.93	5
7	22.125304755	22.143921945	1.86×10⁻²	4.81×10⁻³	22.125316688	1.19×10⁻⁵	0.06	8.89×10⁻⁵	1.85	2
8	28.486387871	28.560421560	7.40×10⁻²	1.09×10⁻²	28.486493560	1.06×10⁻⁴	0.14	4.06×10⁻⁴	3.74	3
9	27.163609617	29.207708099	2.04×10⁰	4.41×10⁻²	27.179901316	1.63×10⁻²	0.80	1.15×10⁻²	26.16	6
10	35.578254236	35.767316820	1.89×10⁻¹	1.90×10⁻²	35.578729685	4.75×10⁻⁴	0.25	1.09×10⁻³	5.76	4
11	35.780085885	38.709492937	2.93×10⁰	5.95×10⁻²	35.815415938	3.53×10⁻²	1.21	2.16×10⁻²	36.35	7
12	43.038408009	43.423183936	3.85×10⁻¹	3.01×10⁻²	43.039902934	1.49×10⁻³	0.39	2.41×10⁻³	8.00	5

下载: 导出CSV

表 5 例2第26阶特征对有限元解与超收敛解收敛阶

Table 5 Rate of convergence of FE solution and recovered solutions on 26th eigenpair in Example 2

$m = 3$					$\bar m = {\rm{4}}$
$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^h}\|$	$r$	$\|\|{{d}} - {{{d}}^h}\|\|$	$r$	$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$r$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$r$
16	3.0092×10⁻¹	−	8.6231×10⁻¹	−	16	1.1674×10⁻²	−	8.4742×10⁻¹	−
32	5.8019×10⁻³	5.7	2.5207×10⁻³	8.4	32	4.4443×10⁻⁵	8.0	2.0138×10⁻⁴	12.0
64	9.5518×10⁻⁵	5.9	1.4991×10⁻⁴	4.1	64	1.7980×10⁻⁷	7.9	5.2408×10⁻⁶	5.3
128	1.5120×10⁻⁶	6.0	9.2470×10⁻⁶	4.0	128	7.0914×10⁻¹⁰	8.0	1.5277×10⁻⁷	5.1
256	2.3701×10⁻⁸	6.0	5.7601×10⁻⁷	4.0	256	2.7769×10⁻¹²	8.0	4.6824×10⁻⁹	5.0
512	3.7063×10⁻¹⁰	6.0	3.5970×10⁻⁸	4.0	512	1.0854×10⁻¹⁴	8.0	1.4560×10⁻¹⁰	5.0
理论值		6		4	理论值		8		5

$\bar m = {\rm{5}}$					$\bar m = {\rm{6}}$
$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$r$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$r$	$ne$	$\|\varOmega {\rm{ - }}{\varOmega ^{\rm{*}}}\|$	$r$	$\|\|{{d}} - {{{d}}^{\rm{*}}}\|\|$	$r$
16	2.2943×10⁻³	−	8.4742×10⁻¹	−	16	2.1079×10⁻³	−	8.4742×10⁻¹	−
32	4.2573×10⁻⁷	12.4	1.4481×10⁻⁴	12.5	32	2.1331×10⁻⁷	13.3	1.4365×10⁻⁴	12.5
64	2.5609×10⁻¹⁰	10.7	2.4027×10⁻⁶	5.9	64	4.1349×10⁻¹¹	12.3	2.3581×10⁻⁶	5.9
128	2.2096×10⁻¹³	10.2	3.8469×10⁻⁸	6.0	128	9.4404×10⁻¹⁵	12.1	3.7307×10⁻⁸	6.0
256	2.0927×10⁻¹⁶	10.0	6.0524×10⁻¹⁰	6.0	256	2.2647×10⁻¹⁸	12.0	5.8473×10⁻¹⁰	6.0
512	2.0281×10⁻¹⁹	10.0	9.4732×10⁻¹²	6.0	512	5.5045×10⁻²²	12.0	9.1435×10⁻¹²	6.0
理论值		10		6	理论值		12		6

下载: 导出CSV

表 6 例3三类轴线曲梁的无量纲频率

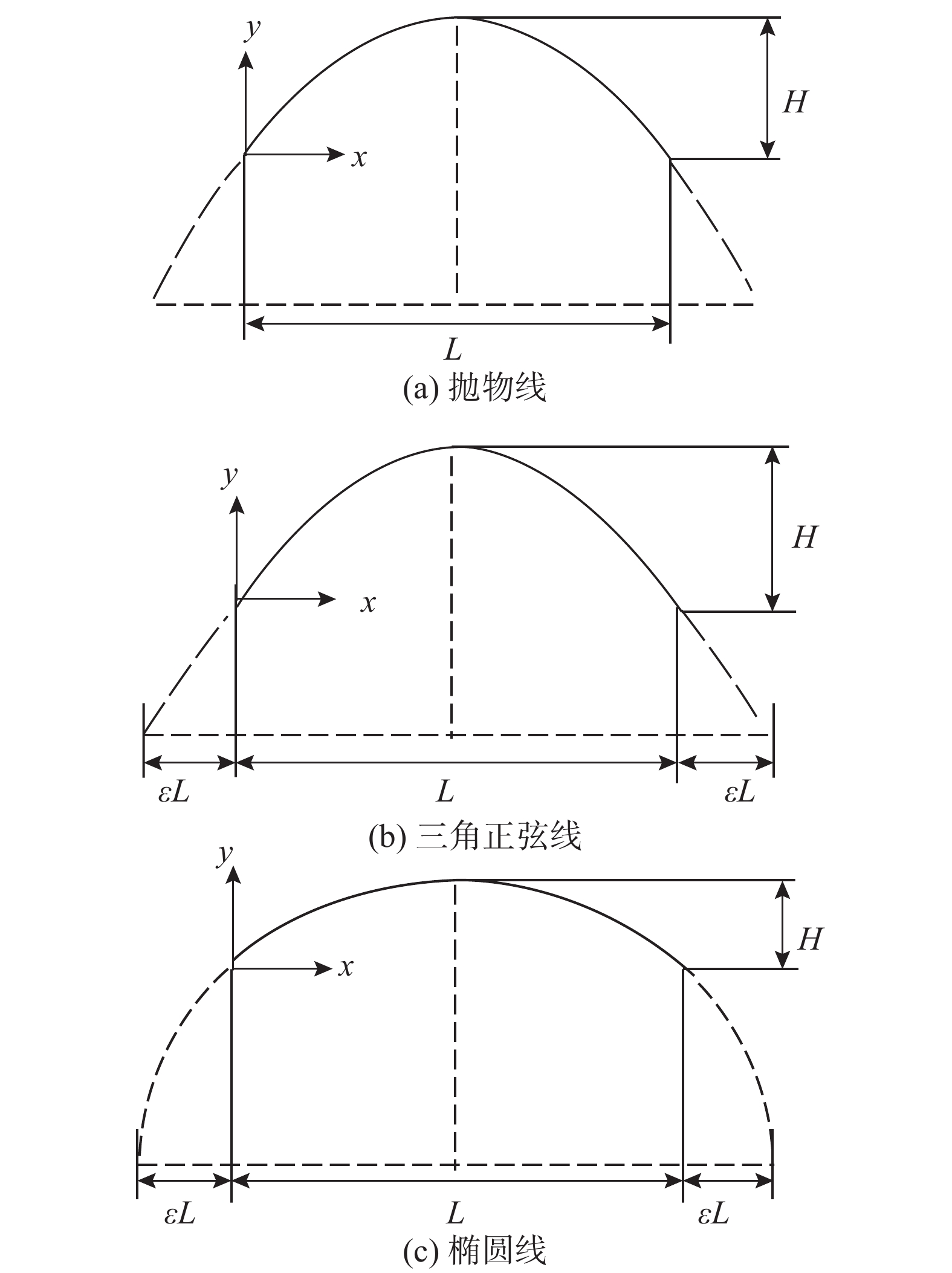
Table 6 Dimensionless frequencies for three curved beams of Example 3

轴线与支座	阶数	文献[27]	文献[28]	$m = {\rm{1}}$ ， $\bar m = {\rm{2}}$				$m = {\rm{2}}$ ， $\bar m = {\rm{3}}$
轴线与支座	阶数	文献[27]	文献[28]	有限元解	误差/(%)	超收敛解	误差/(%)	有限元解	误差/(%)	超收敛解	误差/(%)
抛物线铰支-铰支	1	6.0825	6.090	7.813	28.45	6.095	0.21	6.083	0.00	6.082	0.00
	2	30.4026	30.40	35.739	17.55	30.426	0.08	30.405	0.01	30.402	0.00
	3	70.0449	70.03	81.753	16.71	70.122	0.11	70.048	0.00	70.032	−0.02
三角正弦线固支-固支	1	17.0609	17.14	20.088	17.74	17.068	0.04	17.064	0.02	17.061	0.00
	2	48.5761	48.95	56.542	16.40	48.609	0.07	48.593	0.03	48.575	0.00
	3	95.0274	96.05	107.806	13.45	101.690	7.01	95.075	0.05	95.020	−0.01
椭圆线铰支-固支	1	11.0158	11.04	13.299	20.73	11.034	0.16	11.017	0.01	11.016	0.00
	2	38.6820	38.82	45.353	17.24	38.722	0.10	38.691	0.02	38.682	0.00
	3	81.9146	82.33	95.626	16.74	82.051	0.17	81.947	0.04	81.911	0.00

下载: 导出CSV

表 7 例3前20阶振型计算总耗时

Table 7 Total computation time for first 20 modes of Example 3 /s

轴线	有限元解1 (m=1)	超收敛解1 ( $\bar m = 2$ )	有限元解2 (m=2)	超收敛解2 ( $\bar m = 3$ )
a)	12.204	0.063	30.223	0.105
b)	13.180	0.067	37.097	0.162
c)	14.292	0.084	38.639	0.146

下载: 导出CSV

表 8 超收敛解的收敛阶

Table 8 Convergence order of recovered solutions

收敛阶	${\omega ^*}$	${{{d}}^{\rm{*}}}$
$r$	$\min (2\bar m,4m)$	$\min (\bar m + 1,2m)$

下载: 导出CSV

参考文献(28)

[1]	Strang G, Fix G J. An analysis of the finite element method [M]. Englewood Cliffs, NJ: Prentice-Hall, 1973.
[2]	Yang F, Sedaghati R, Esmailzadeh E. A finite thin circular beam element for out-of-plane vibration analysis of curved beams [J]. Journal of Mechanical Science and Technology, 2009, 23(5): 1396 − 1405. doi: 10.1007/s12206-008-1213-2
[3]	Wu J S. Analytical and numerical methods for vibration analyses [M]. Hoboken, NJ: John Wiley & Sons, 2015: 483 − 607.
[4]	Kaan Kaygisiz. Out-of-plane vibrations of planar curved beams having variable curvature and cross-section [D]. İzmir: İzmir Institute of Technology, 2012: 1 − 34.
[5]	Kang K, Bert C W, Striz A G. Vibration analysis of shear deformable circular arches by the differential quadrature method [J]. Journal of Sound & Vibration, 1995, 183(2): 353 − 360.
[6]	孙广俊, 李鸿晶, 王通, 邢浩洁. 基于DQM的曲梁平面外固有振动特性及参数分析[J]. 工程力学, 2013, 30(12): 220 − 227. Sun Guangjun, Li Hongjing, Wang Tong, Xing Haojie. Out-of-plane natural vibration characteristic and parameter analysis of curved girders based on DQM [J]. Engineering Mechanics, 2013, 30(12): 220 − 227. (in Chinese)
[7]	Jinhee Lee. Free vibration analysis of circularly curved multi-span Timoshenko beams by the pseudospectral method [J]. Journal of Mechanical Science and Technology, 2007, 21(12): 2066 − 2072. doi: 10.1007/BF03177465
[8]	Howson W P, Jemah A K. Exact dynamic stiffness method for planar natural frequencies of curved Timoshenko beams [J]. Journal of Mechanical Engineering Science, 1999, 213(7): 687 − 696. doi: 10.1177/095440629921300704
[9]	Huang C S, Tseng Y P, Chang S H, Hung C L. Out-of-plane dynamic analysis of beams with arbitrarily varying curvature and cross-section by dynamic stiffness matrix method [J]. International Journal of Solids and Structures, 2000, 37(3): 495 − 513. doi: 10.1016/S0020-7683(99)00017-7
[10]	叶康生, 赵雪健. 动力刚度法求解平面曲梁面外自由振动问题[J]. 工程力学, 2012, 29(3): 1 − 8. Ye Kangsheng, Zhao Xuejian. Dynamic stiffness method for out-of-plane free vibration analysis of planar curved beams [J]. Engineering Mechanics, 2012, 29(3): 1 − 8. (in Chinese)
[11]	Wiberg N E, Bausys R, Hager P. Improved eigenfrequencies and eigenmodes in free vibration analysis [J]. Computers & Structures, 1999, 73(1 − 5): 79 − 89.
[12]	林群, 杨一都. 解二阶椭圆本征值问题的有限元插值校正方法[J]. 计算数学, 1992, 14(3): 334 − 338. Lin Qun, Yang Yidu. The finite element interpolated correction method for second order elliptic eigenvalue problems [J]. Mathematica Numerica Sinica, 1992, 14(3): 334 − 338. (in Chinese)
[13]	龚国庆, 范子杰, 刘寒冰. 基于应力超收敛恢复技术的广义特征值问题后验误差估计[J]. 工程力学, 2004, 21(3): 111 − 117. doi: 10.3969/j.issn.1000-4750.2004.03.021 Gong Guoqing, Fan Zijie, Liu Hanbing. A posteriori error estimation based on stress super-convergence recovery technique for generalized eigenvalue problems [J]. Engineering Mechanics, 2004, 21(3): 111 − 117. (in Chinese) doi: 10.3969/j.issn.1000-4750.2004.03.021
[14]	Avrashi J, Cook R D. New error estimation for C0 eigenproblems in finite element analysis [J]. Engineering Computations, 1993, 10(3): 243 − 256. doi: 10.1108/eb023905
[15]	Wang D, Liu W, Zhang H. Novel higher order mass matrices for isogeometric structural vibration analysis [J]. Computer Methods in Applied Mechanics & Engineering, 2013, 260(9): 92 − 108.
[16]	Wang D, Liu W, Zhang H. Superconvergent isogeometric free vibration analysis of Euler-Bernoulli beams and Kirchhoff plates with new higher order mass matrices [J]. Computer Methods in Applied Mechanics & Engineering, 2015, 286(4): 230 − 267.
[17]	Li M X, Lin Q, Zhang S H. Extrapolation and superconvergence of the Steklov eigenvalue problem [J]. Advances in Computational Mathematics, 2010, 33(1): 25 − 44. doi: 10.1007/s10444-009-9118-7
[18]	Huang P Z. Superconvergence of a stabilized approximation for the stokes eigenvalue problem by projection method [J]. Applications of Mathematics, 2014, 59(4): 361 − 370. doi: 10.1007/s10492-014-0061-7
[19]	叶康生, 曾强. 结构自由振动问题有限元新型超收敛算法研究[J]. 工程力学, 2017, 34(1): 45 − 50, 68. Ye Kangsheng, Zeng Qiang. A new superconvergent recovery method for FE analysis on structural free vibration problems [J]. Engineering Mechanics, 2017, 34(1): 45 − 50, 68. (in Chinese)
[20]	叶康生, 姚葛亮. 平面曲梁有限元静力分析的p型超收敛算法[J]. 工程力学, 2017, 34(11): 26 − 33, 58. Ye Kangsheng, Yao Geliang. A p-type superconvergent recovery method for FE static analysis of planar curved beams [J]. Engineering Mechanics, 2017, 34(11): 26 − 33, 58. (in Chinese)
[21]	叶康生, 殷振炜. 平面曲梁面内自由振动有限元分析的p型超收敛算法[J]. 工程力学, 2019, 36(5): 28 − 36, 52. Ye Kangsheng, Yin Zhenwei. A p-type superconvergent recovery method for FE analysis of in-plane free vibration of planar curved beams [J]. Engineering Mechanics, 2019, 36(5): 28 − 36, 52. (in Chinese)
[22]	叶康生, 殷振炜. 欧拉梁弹性稳定分析的有限元p型超收敛算法[J]. 力学与实践, 2018, 40(6): 647 − 652. Ye Kangsheng, Yin Zhenwei. A p-type superconvergent recovery method for FE elastic stability analysis of Euler beams [J]. Mechanics in Engineering, 2018, 40(6): 647 − 652. (in Chinese)
[23]	叶康生, 邱廷柱. 二阶非线性常微分方程边值问题有限元p型超收敛计算[J]. 工程力学, 2019, 36(12): 7 − 14. Ye Kangsheng, Qiu Tingzhu. A p-type superconvergent recovery method for FE analysis on boundary value problems of second-order nonlinear ordinary differential equations [J]. Engineering Mechanics, 2019, 36(12): 7 − 14. (in Chinese)
[24]	Chidamparam P, Leissa A W. Vibrations of planar curved beams, rings, and arches [J]. Applied Mechanics Reviews, 1993, 46(9): 467 − 483. doi: 10.1115/1.3120374
[25]	Douglas J, Dupont T. Galerkin approximations for the two point boundary problems using continuous piecewise polynomial spaces [J]. Numerical Mathematics, 1974, 22(2): 99 − 109. doi: 10.1007/BF01436724
[26]	Howson W P, Jemah A K. Exact out-of-plane natural frequencies of curved Timoshenko beams [J]. Journal of Engineering Mechanics, 1999, 125(1): 19 − 25. doi: 10.1061/(ASCE)0733-9399(1999)125:1(19)
[27]	Rajasekaran S. Analysis of curved beams using a new differential transformation based curved beam element [J]. Meccanica, 2014, 49(4): 863 − 886. doi: 10.1007/s11012-013-9835-3
[28]	Byoung Koo Lee, Sang Jin Oh, Jeong Man Mo, Tae Eun Lee. Out-of-plane free vibrations of curved beams with variable curvature [J]. Journal of Sound & Vibration, 2008, 318(1/2): 227 − 246.

施引文献(39)

期刊类型引用(16)

1.	FENG Xian-dao，ZHANG Zuo-jin，FANG Hui，LI Hua-jun. Seismic Performance of a Circular Steel Tube-RC Structure with UHPC Grouted Filled. China Ocean Engineering. 2025(01): 111-124 . 必应学术
2.	姜磊，刘永健，周绪红，陈宝春，牟廷敏，刘君平，陈洪明. 钢管混凝土组合结构桥梁设计原理与技术发展综述. 中国公路学报. 2025(03): 278-302 . 百度学术
3.	杜国锋，曹煊，谢向东，张继承. 高强钢管超高性能混凝土界面黏结滑移性能试验. 河南理工大学学报(自然科学版). 2024(01): 180-188 . 百度学术
4.	李俊华，王维宸，周春恒，陈志辉. 冻融循环环境下方钢管混凝土粘结强度试验研究. 工程力学. 2024(S1): 206-214 . 本站查看
5.	冯先导，刘聪聪，林红星. 预制桩芯桩帽结构承载性能及安装工艺试验研究. 水运工程. 2024(11): 215-220 . 百度学术
6.	朱张峰，RICHARD Liew，杜咏，姚兵. 装配式组合结构柱高强钢管连接节点界面黏结性能试验. 工业建筑. 2023(04): 120-124+179 . 百度学术
7.	王占锋，谢东武. 超高强钢筋混凝土抗腐蚀性影响因素研究. 科技通报. 2022(01): 77-83 . 百度学术
8.	廖栩，李吉人，王庆利. 轴压荷载下中空夹层钢管混凝土抗扭性能试验研究. 建筑结构. 2022(06): 90-96+125 . 百度学术
9.	曾彦钦，徐礼华，吴方红，余敏，池寅. 钢管含粗骨料超高性能混凝土短柱轴压性能研究. 工程力学. 2022(10): 68-78 . 本站查看
10.	王秋维，梁林，史庆轩，王朋. 方钢管超高性能混凝土界面黏结滑移性能. 湖南大学学报(自然科学版). 2022(11): 116-125 . 百度学术
11.	程高，张之恒，谢亮，姬子田. 基于桁梁实桥试验的钢管混凝土界面传力机制. 交通运输工程学报. 2022(06): 158-168 . 百度学术
12.	张萍. 水工建筑物超高强混凝土抗腐蚀性能的影响规律研究. 黑龙江水利科技. 2022(11): 35-39 . 百度学术
13.	高春彦，原淼淼，王佳丽，孙凯琦，赵宁. 钢管UHPC界面粘结滑移力学性能研究. 建筑结构. 2022(S2): 1369-1374 . 百度学术
14.	谢磊，李庆华，徐世烺. 冲击荷载下免蒸养活性粉末混凝土分形特征研究. 工程力学. 2021(03): 169-180 . 本站查看
15.	廖栩，李吉人，王庆利. 压-扭作用下中空夹层钢管混凝土的破坏机理分析. 混凝土与水泥制品. 2021(12): 67-74 . 百度学术
16.	陈宝春，李莉，罗霞，韦建刚，赖秀英，刘君平，丁庆军，李聪. 超高强钢管混凝土研究综述. 交通运输工程学报. 2020(05): 1-21 . 百度学术