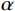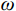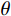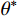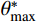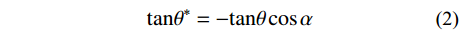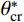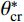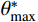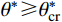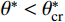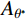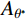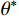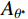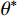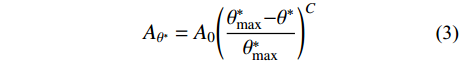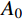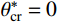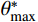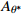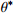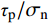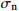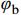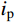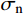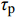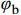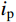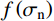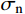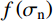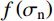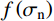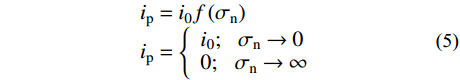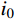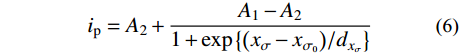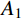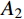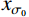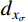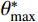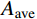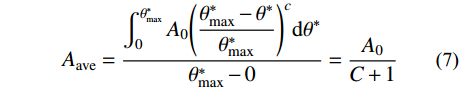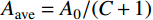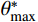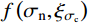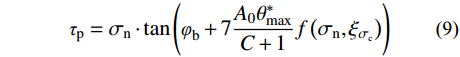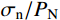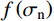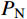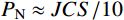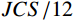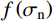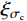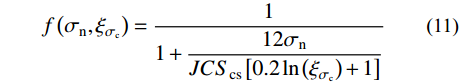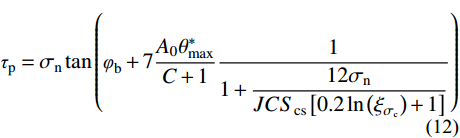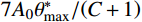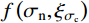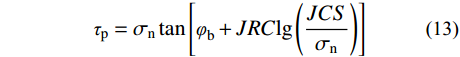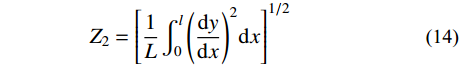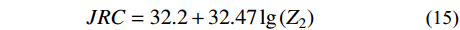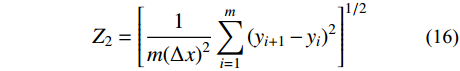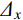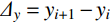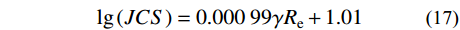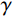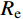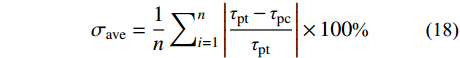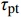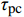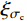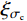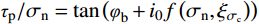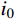CALCULATION MODEL FOR THE SHEAR STRENGTH OF SOFT-HARD JOINTS BASED ON THREE-DIMENSIONAL MORPHOLOGY AND DILATANCY EFFECT
-
摘要: 上、下盘抗压强度不一致的软-硬节理的抗剪强度难以准确获取,应用Barton模型等常用的岩石节理抗剪强度模型也不能准确表征这类特殊节理的抗剪强度。借助三维激光扫描和3D打印技术,浇筑了具有自然节理形貌上下盘抗压强度相同以及上下盘抗压强度不同的人工节理试样,并对其进行常法向应力下的剪切试验。分析了法向应力、三维形貌特征以及节理强度比对软-硬节理的抗剪强度和剪胀角的影响。试验结果表明:节理抗剪强度与法向应力、节理强度比和节理粗糙度呈正相关;剪胀角与法向应力呈负相关,与节理强度比和节理粗糙度呈正相关。通过研究剪胀角在剪切过程中随法向应力和节理强度比的演化规律,建立了含有三维形貌参数和节理强度比的岩石节理抗剪强度模型。通过与Barton模型的对比分析,验证了所提出模型的可靠性。采用该文模型计算云南某水电站库区内不稳定斜坡平硐内出现的软-硬节理的抗剪强度,计算结果和试验值较为接近,论证了该模型的适用性。Abstract: It is difficult to accurately obtain the shear strength of soft-hard joints of hanging walls and footwalls with different compressive strengths. The shear strength of such special joints cannot be accurately characterized by the commonly used rock joint shear strength models such as the Barton models. We used three-dimensional laser scanning and three-dimensional printing technology to pour artificial joint samples that have the natural joint morphology and the same or different compressive strengths of the hanging walls and footwalls. Shear tests under normal stress were carried out on the samples to analyze the effects of normal stress, three-dimensional morphology and joint strength ratio on the shear strength and dilatancy angle of soft-hard joints. The test results revealed that the shear strength of the joints was positively correlated with the normal stress, joint strength ratio and joint roughness, and that the dilatancy angle was inversely correlated with the normal stress, and positively correlated with the joint strength ratio and joint roughness. By studying the evolution law of the dilatancy angle with the normal stress and the joint strength ratio in the shear process, we established a shear strength model of rock joint with three-dimensional morphology parameters and the joint strength ratio. The reliability of the proposed model was verified by comparison with the Barton model. The model was used to calculate the shear strength of the soft-hard joints in the adit of the unstable slope in the reservoir area of a hydropower station in Yunnan Province. The calculation results were similar to the test values, which proved the applicability of the model.
-
节理是一种十分常见的地质构造,较为普遍的出现在岩体中,其不连续性极大地影响着岩体的力学性质,对人类的工程建设活动造成了一定程度的困扰[1-2]。岩体节理抗剪强度计算在岩土工程领域起着重要作用,是岩质边坡等稳定性评价的重要依据。
节理的剪切强度特性一直是国内外学者研究的热点。Patton[3]研究了锯齿状人工节理在不同法向应力下的剪切强度,将剪胀效应引入摩尔-库仑准则中建立了双线性强度包络线。此后大量学者以Patton的理论为基础,用各类参数表征峰值剪胀角在节理剪切过程中的变化规律,从而建立各自的岩石节理抗剪强度模型。Maksimović[4]采用节理粗糙角Δφ和中位角压力值PN表示峰值剪胀角,建立非线性岩石节理抗剪强度模型。肖卫国等[5] 基于岩体节理变形的非线性特征,针对剪切过程中节理微凸体的磨损与破碎而导致的应力下降,提出了考虑峰后软化的切向变形的本构模型。尹显俊等[6]研究了岩体结构面循环加载的强度,并建立了本构模型。Kulatilake等[7]引入固定粗糙度参数SRP和平均倾角I建立岩石节理抗剪强度模型。Barton[8]以大量岩石节理的剪切试验为基础,采用节理粗糙度系数JRC和节理抗压强度系数JCS共同表示剪胀角随法向应力的变化规律,提出了经典的JRC-JCS岩石节理抗剪强度模型。Wei等[9]采用三轴试验对Barton模型的可靠性以及适用范围进行了论证。
Patton[3]通过大量的现场及室内试验研究,证实了节理面的粗糙程度对节理的剪切强度有十分显著的影响。节理粗糙度的评价是确定节理抗剪强度的关键因素。Barton和Choubey[10]提出了10条标准节理剖面线,用以对比确定粗糙度系数JRC的值,从而判定节理的粗糙程度。该方法简单有效,被国际岩石力学学会(ISRM)采纳为岩石节理粗糙度评价的标准方法。但是目测对比确定节理粗糙度,存在一定的人为主观因素,为了规避这一缺陷,大量学者致力于研究如何定量描述节理粗糙度。从二维到三维提出了各类参数,用以量化评估节理面的粗糙程度。Tse和Cruden[11]以一条贯穿节理剖面的中心线CLA为基础,提出了一阶导数均方根Z2以及结构函数SF,并建立了JRC和Z2以及SF的函数关系式,从而量化评估节理粗糙程度。因该方法简单有效而被广泛应用,随后有学者对一阶导数均方根Z2进行了改进[12],或采用不同的处理手段对Z2和JRC进行拟合[13]。大量学者借助数理统计的方法提出了许多用以表征节理粗糙度的参数,如:角度标准差SDi[14];正、负向坡度参数
S+p 、S−p [15];节理剖面的迹线长度与其直线长度的比值Rp[16]等。Grasselli等[17-19]借助高精度的三维扫描仪对节理面扫描后,离散化成微小的三角单元,提出了临界视倾角
θ∗cr 的概念简化了剪切机理,建立了潜在接触面积比Aθ∗ 和视倾角θ*之间的高次抛物函数关系,并采用最大潜在接触面积比A0、最大视倾角θ∗max 和粗糙度参数C来定量描述节理面的三维形貌特征,从而建立了基于三维形貌参数的岩石节理抗剪强度模型。此类参数能较好地描述节理面的形貌特征对节理剪切强度的影响,因此得到广泛的应用。许多学者基于Grasselli的三维形貌参数提出了各自的岩石节理抗剪强度模型[20-24]。目前关于岩石节理的研究,主要集中于上、下盘抗压强度相同的常规节理,对于上、下盘抗压强度不一致的软-硬节理的研究较为少见。Nasir等[25]研究了矿山回填中胶结填充体(CPB)与围岩的剪切特性。Wu等[26]以三峡地区的泥岩与泥质灰岩的层面为研究对象,建立了神经网络用以预测软-硬节理的抗剪强度。Ghazvinian等[27]研究了软硬互层的岩质边坡的层面,以此为基础对Barton模型进行改进。宋磊博等[28]采用等效节理抗压强度反映软-硬节理在剪切过程中的抗压强度系数,从而对Barton模型进行修正。
自然界中岩石节理形貌多样复杂,学者的研究长期受困于节理试验的不可重复性,而水泥砂浆浇筑的人工节理解决了这一难题,但受限于技术,以往人工节理的研究多是简单的锯齿状[3,26-27]。随着3D打印技术的成熟以及和光学扫描技术的结合,采用水泥砂浆仿制天然节理形貌的人工节理试样,使相同节理的重复试验成为可能[29]。伴随着科学技术的进步,更多的仪器设备支持着科研工作者的研究,CT扫描仪以及三维光学扫描仪越来越多的应用于岩土工程领域的研究,打开了岩石节理研究的细观领域。CT扫描技术多用于岩石的细观损伤特性的研究[30],而三维光学扫描技术常用于采集节理面形貌特征等信息。Jiang等[31]将基于3D打印技术制作的人工节理和天然节理进行对比,证实了3D技术的可靠性。Head等[32]采用3D打印技术,打印出岩石内部的微观特征,用于研究岩石微观结构变化对渗透率的影响。肖维民等[33]将3D打印技术用于柱状节理的研究。刘泉声等[34]采用Visijet PXL类石膏作为3D打印的原料,打印出仿真的岩石试样。
本文借助三维激光扫描技术和3D打印技术制作人工节理模具,采用水泥砂浆浇筑与天然节理形貌相同的人工节理试样,其中包括上、下盘抗压强度一致和上、下盘抗压强度不一致的人工节理,在此基础上开展试验研究。为表征节理上、下盘抗压强度不一致的特性,定义了节理强度比[28],如式(1)所示。
ξσc=σchσcs (1) 式中:
ξσc 为节理强度比;σch 为节理较硬盘的抗压强度;σcs 为节理较软盘的抗压强度。对人工节理试样进行常法向应力下的剪切试验。根据试验结果,分析了不同三维形貌以及不同节理强度比对节理剪切强度特性的影响。将试验结果和理论推导结合,建立含有三维形貌参数以及节理强度比适用于软-硬节理的抗剪强度模型。并对所建立模型的适用性及可靠性进行了深入的探讨和研究。
1 人工节理的室内试验
1.1 人工节理试样的制作
常法向应力剪切试验(CNL)一直被认为是测试岩石节理强度特性和变形特性的有效手段。以往的研究受限于自然节理的复杂多样,不能制备相同的节理试样,无法进行同一个节理形貌在多个法向应力下的剪切对比。故而本文选用天然节理的水泥砂浆复制品替代进行试验。
采用三维激光扫描仪对取自某大型深基坑内的节理岩样进行扫描,扫描过程如图1所示。
扫描后,提取研究区域的节理面信息,在后处理软件中建立节理的三维实体,将三维实体切片后,导入3D打印机,打印制作人工节理模具。人工节理模具的制作过程如图2所示。
为提高试验的精确性,在制样过程中严格控制水泥砂浆的配比以及砂和水泥的选料。选用标准砂和早强水泥,经过调试对比确定三种不同强度(高、中、低)的水泥砂浆,用于浇筑不同抗压强度的节理盘,不同配合比水泥砂浆的基本参数见表1。
表 1 不同配比水泥砂浆的基本参数Table 1. Basic parameters of cement mortar with different proportions强度级别 配合比
水∶灰∶砂单轴抗压强度σc/MPa 弹性模量 E/GPa 低 1∶2∶5 20.31 4.07 中 1∶2.5∶4 43.25 5.94 高 1∶3∶3 62.53 7.53 根据以往的试验经验,砂浆在浇筑振捣和凝固的过程中,内部气体多由上表面溢出。若将人工节理模具置于上部,采取压模的形式制作人工节理,极易出现蜂窝麻面等情况,对节理试样表面的抗压强度产生较大的影响。故而浇筑人工节理时,将人工节理模具水平放置于浇筑盒底部并固定,防止浇筑时发生偏移。而后在浇筑盒内壁均匀的涂上液体脱模剂,将水泥砂浆分层加料至浇筑盒内,置于振动台上,高频轻振,充分振捣,排出砂浆内部气体,当浇筑至浇筑盒顶部后,将其抹平。人工节理的浇筑过程如图3所示。
按照上述人工节理的制作流程,采用低强度水泥砂浆浇筑3种不同粗糙度的人工节理。3组人工节理分别记为K-I、K-II、K-III,每组5个试样。用于做相同节理强度比、不同粗糙度条件下节理剪切试验的对比分析。
对于节理模型K-III组,再浇筑两组不同强度比的人工节理试样。分别为:中强度水泥砂浆浇筑下盘,低强度水泥砂浆浇筑上盘的K-III-2组;以及高强度水泥砂浆浇筑下盘,低强度水泥砂浆浇筑上盘的K-III-3组,每组5个试样。K-III、K-III-2、K-III-3三组人工节理试样用于做相同粗糙度、不同节理强度比条件下节理剪切试验的对比分析。各组人工节理的水泥砂浆使用情况见表2。
表 2 人工节理的基本参数Table 2. Basic parameters of artificial joints组别 节理材料强度级别 强度比ξσc 基本摩擦角φb/(°) 上盘 下盘 K-I 低 低 1.00 31.0 K-II 低 低 1.00 K-III 低 低 1.00 K-III-2 低 中 2.13 31.9 K-III-3 低 高 3.08 32.5 采用成都理工大学地质灾害防治与地质环境保护国家重点实验室的岩体剪切试验仪,对养护好的人工节理试件进行常法向应力下的剪切试验。每组试样共进行五级法向应力下的剪切,五级法向应力分别为0.5 MPa、1.0 MPa、1.5 MPa、2.0 MPa、3.0 MPa。试验开始时采用应力控制法,施加法向应力达到预定荷载后,采用位移控制法,施加剪切应力直至试验结束。剪切加载速率始终保持为1.0 mm/min,设定剪切位移为15 mm,保证出现残余抗剪强度或试样破坏不能继续剪切。
1.2 节理面的三维量化
Hopkins[35]认为,对于承受法向应力的岩石节理,总接触面积通常远小于节理表面的70%。Grasselli等[17-19]观察剪切后的节理面变化特征,证实在真实的节理剪切过程中,实际接触面积仅占节理表面的一部分,且接触部分的分布具有明显的随机性,很难通过节理粗糙系数JRC这样的二维剖面来表征。本文采用三维激光扫描仪对人工节理试样进行扫描,提取高程信息,采样间距为0.3 mm。
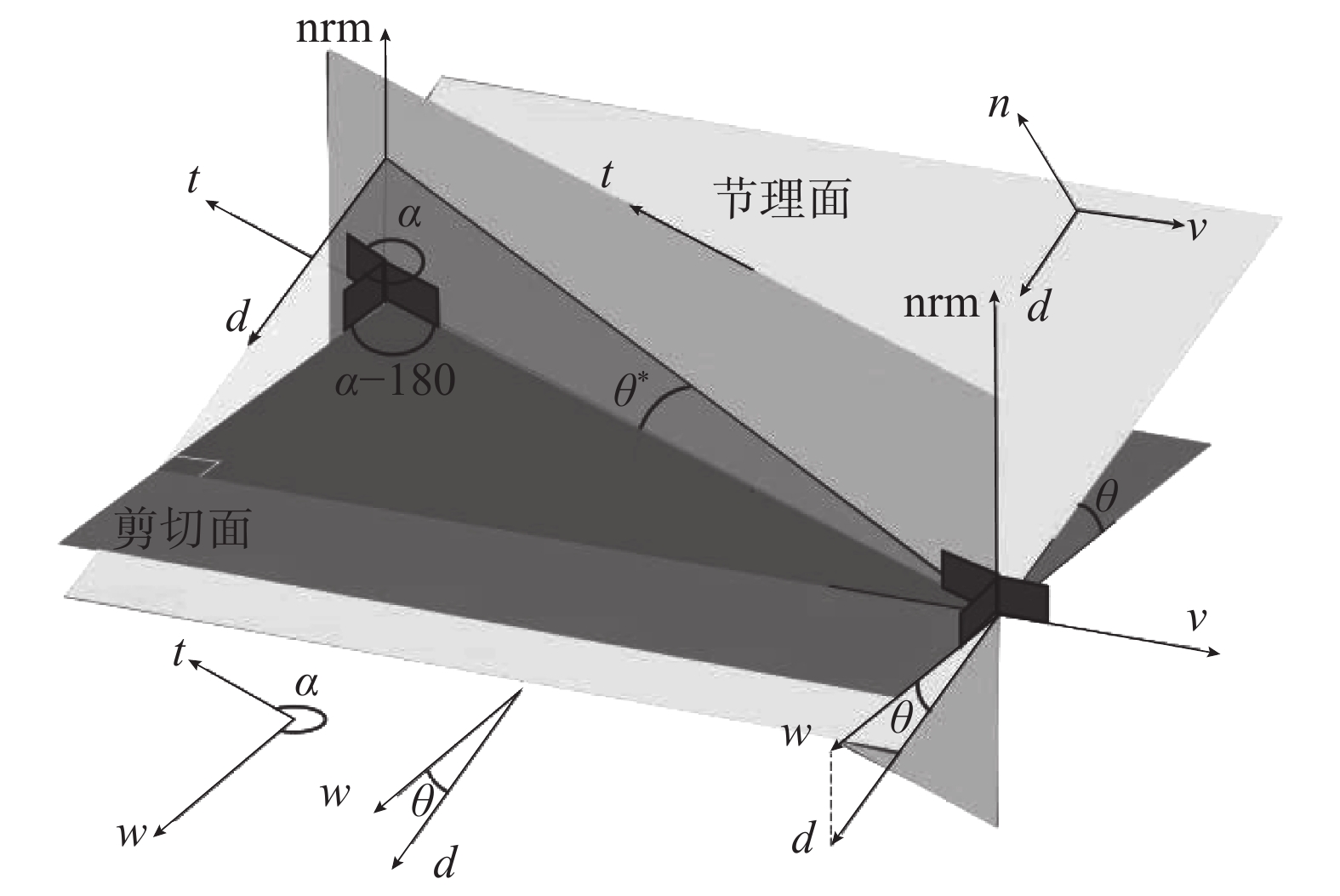
Grasselli将节理面扫描后离散化,以每个小三角形作为一个微单元。如图4所示,方位角
α 是节理微单元倾角向量d在剪切平面ω 上的投影与剪切向量t的夹角。倾角θ 是剪切面与节理微单元的夹角。节理的接触取决于节理微单元沿剪切方向上的视倾角θ∗ 的大小。视倾角计算式(2)。所有节理微单元中沿剪切方向上视倾角最大的角度,称为最大视倾角θmax 。{\rm{tan}}{\theta ^*} = {\rm{ - tan}}\theta \cos \alpha (2) 节理剪切时,潜在磨损(碎)区仅发生在面向剪切方向上较陡部分的微单元。因此只有微单元的倾角较大时,才能对节理剪切的力学行为产生直接影响。剪切时不同法向应力和不同剪切方向均存在一个临界视倾角
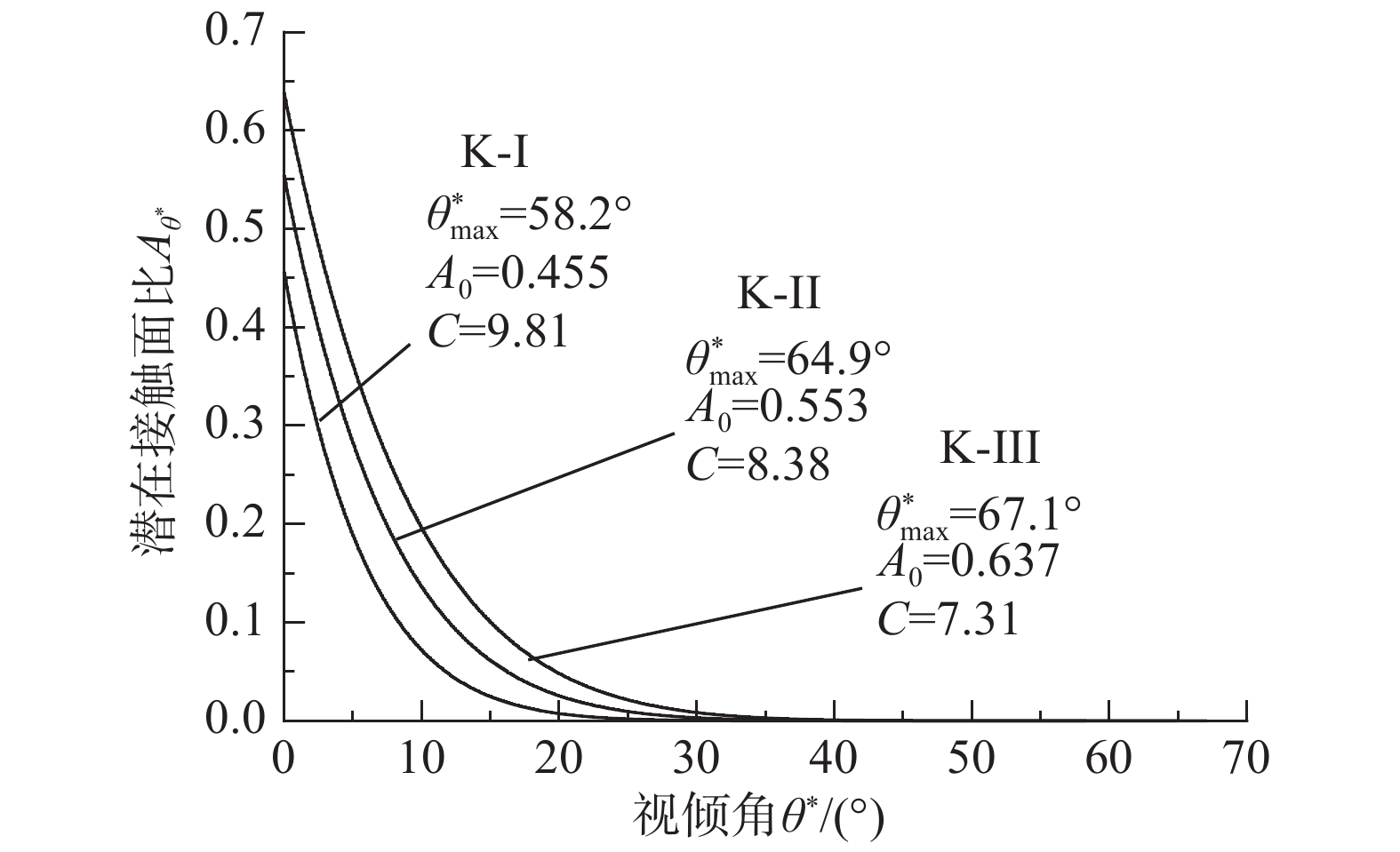
\theta _{\rm{cr}}^{{*}} 。临界视倾角\theta _{\rm{cr}}^{{*}} 的取值范围在0到最大视倾角\theta _{\rm max }^{{*}} 之间。当节理微单元视倾角大于临界视倾角时{\theta ^ * } \geqslant \theta _{{\rm cr}}^{{*}} ,为节理面的潜在接触区域;当节理微单元视倾角小于临界视倾角时{\theta ^ * } < \theta _{{\rm{cr}}}^ * ,为非接触区域。潜在接触区域的面积总和与节理面总面积的比值称为潜在接触面积比{A_{{\theta ^*}}} 。Grasselli采用高次函数描述节理面潜在接触面积比{A_{{\theta ^*}}} 与视倾角{\theta ^*} 之间的关系,如式(3)所示。本文三种人工节理面的潜在接触面积比{A_{{\theta ^ * }}} 与视倾角{\theta ^ * } 的关系如图5所示。{A_{{\theta ^*}}} = {A_0}{\left( {\frac{{\theta _{\max }^*{\rm{ - }}{\theta ^{\rm{*}}}}}{{\theta _{\max }^{\rm{*}}}}} \right)^{C}} (3) 式中:
{A_0} 为最大潜在接触面积比(临界视倾角\theta _{\rm cr}^* = 0 时);\theta _{\rm max }^{\rm{*}} 为沿剪切方向上节理微单元的最大视倾角;C为粗糙度参数。各组人工节理试样的形貌参数如图5所示。粗糙度参数C表示节理的粗糙程度,C值越小节理面越粗糙。理论上,粗糙度参数C的取值范围可由0到+∞,当C等于0时,节理面为锯齿状,所有节理微单元都具有相同倾角;当C趋于∞时,表示节理是一个光滑的平面。由节理三维形貌参数可知,3组人工节理的粗糙程度按K-III、K-II、K-I依次递减。
对于新鲜的张拉节理或者完全吻合的人工节理,虽然上、下盘的扫描面有所不同,但无论扫描节理的上盘或是下盘,将节理面离散化后,其对应位置的微单元视倾角是相同的。在剪切方向固定的情况下,潜在接触面积比的计算值不会因为节理的上、下盘而改变。故而对于同一个节理的上、下盘,三维形貌参数是一致的。
2 软-硬节理抗剪强度模型的建立
2.1 节理剪切的强度特性及变形特性分析
图6、图7为节理剪切的应力-位移曲线;表3、表4为节理剪切的峰值抗剪强度,由图、表可知:1)图6中,法向应力为0.5 MPa时,试样剪切的前1 mm的位移中,应力没有明显增长,是因为试样与剪切盒未完全贴合存在1 mm左右的空隙,当施加位移超过1 mm后,应力才出现增长;2)在节理剪切初期,剪应力随着剪切位移的增长而快速的增长,剪切刚度近似常量,随着剪切的进行,剪切刚度下降,剪应力在达到峰值后趋于稳定;3)节理强度比不变时,随着法向应力的增大,节理的初始剪切刚度、峰值抗剪强度、残余抗剪强度都随之增大。且抗剪强度和法向应力的比值(
{{{\tau _{\rm p}}} / {{\sigma _{\rm n}}}} )呈非线性下降;4)法向应力不变时,随着节理强度比的增大,节理的初始剪切刚度、峰值抗剪强度、残余抗剪强度都随之增大;5)节理抗剪强度受节理表面三维形貌特征影响,相同法向应力作用下粗糙度越大,节理的抗剪强度越大。表 3 不同粗糙度节理直剪试验结果Table 3. Direct shear test results of joints with different extents of roughness法向应力{\sigma _{{\rm n}}}/MPa K-I K-II K-III {\tau _{{\rm p}}}/MPa {{{\tau _{{\rm p}}}} / {{\sigma _{{\rm n}}}}} {\tau _{{\rm p}}}/MPa {{{\tau _{{\rm p}}}} / {{\sigma _{{\rm n}}}}} {\tau _{{\rm p}}}/MPa {{{\tau _{{\rm p}}}} / {{\sigma _{{\rm n}}}}} 0.5 0.52 1.04 0.64 1.28 0.86 1.72 1.0 0.85 0.85 1.02 1.02 1.28 1.28 1.5 1.21 0.81 1.59 1.06 1.83 1.22 2.0 1.56 0.78 1.89 0.95 2.09 1.05 3.0 2.30 0.77 2.52 0.84 2.86 0.95 表 4 不同强度比节理直剪试验结果Table 4. Direct shear test results of joints with different strength ratios法向应力 {\mathrm{\sigma }}_{\mathrm{n}} /MPa K-III({\xi _{\sigma _{\rm c}} }=1.00) K-III-2({\xi _{\sigma _{\rm c}} }=2.13) K-III-3({\xi _{\sigma _{\rm c}} }=3.08) {\mathrm{\tau }}_{\mathrm{p}} /MPa {\mathrm{\tau }}_{\mathrm{p}} /MPa {\mathrm{\tau }}_{\mathrm{p}} /MPa 0.5 0.86 0.84 0.96 1.0 1.28 1.51 1.57 1.5 1.83 1.90 2.09 2.0 2.09 2.47 2.51 3.0 2.86 3.19 3.15 2.2 软-硬节理抗剪强度模型的建立
节理峰值抗剪强度在低法向应力下满足摩尔-库仑强度准则[3],其形式为:
{\tau _{\rm p}} = {\sigma _{\rm n}}\tan ( {{\varphi _{\rm b}} + {i_{\rm p}}} ) (4) 式中:
{\varphi _{\rm b}} 为基本摩擦角;{i_{\rm p}} 为剪胀角;{\sigma _{\rm n}} 为作用的法向应力;{\tau _{\rm p}} 为节理的抗剪强度。由式(4)可知,岩石节理的抗剪强度由两部分组成:其一,岩石节理的基本摩擦角
{\varphi _{\rm b}} ,取决于节理试样的材料属性;其二,岩石节理的剪胀角{i_{\rm p}} ,取决于岩石节理表面的形貌特征。Maksimović[36]明确了剪胀角的边界条件如式(5)所示。其中剪胀角影响系数
f\left( {{\sigma _{\rm n}}} \right) 与法向应力{\sigma _{\rm n}} 呈负相关。f\left( {{\sigma _{\rm n}}} \right) 的取值范围为0~1,当法向应力趋于∞时,剪胀效应完全被抑制,此时剪胀角为零即影响系数f\left( {{\sigma _{\rm n}}} \right) =0;当法向应力趋于零时,此时节理剪切的剪胀角最大为初始剪胀角即影响系数f\left( {{\sigma _{\rm n}}} \right) =1。\begin{array}{l} {i_{\rm p}} = {i_0}f\left( {{\sigma _{\rm n}}} \right)\\ {i_{\rm p}} = \left\{ \begin{array}{l} {i_0};\;\;\;{\sigma _{\rm n}} \to 0\\ 0;\;\;\;{\sigma _{\rm n}} \to \infty \end{array} \right. \end{array} (5) 式中,
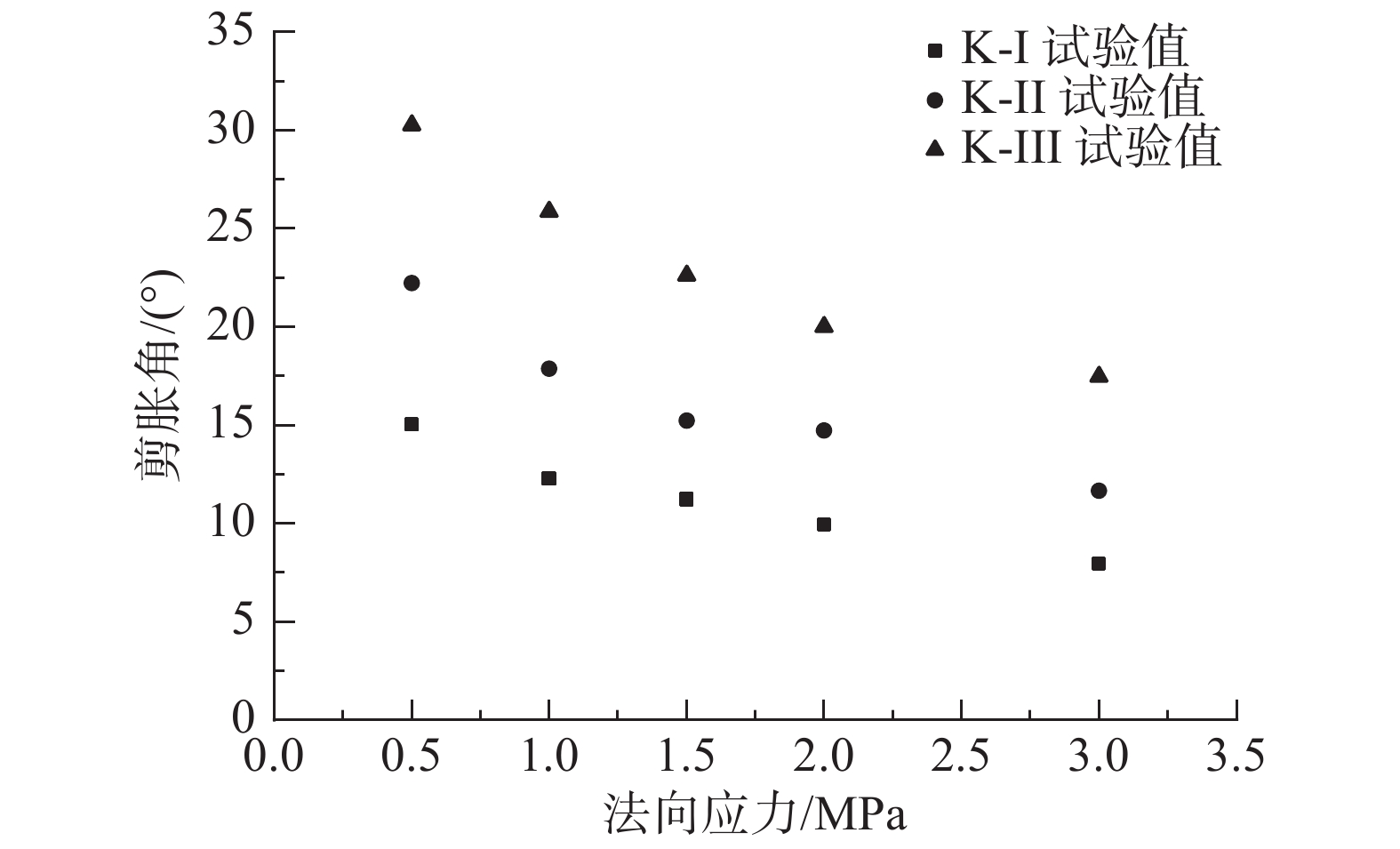
{i_0} 为初始剪胀角(法向应力为零时的剪胀角),为节理的最大剪胀角。图8为直剪试验的峰值剪胀角与法向应力的关系,由图可知:对于三维形貌相同的节理,法向应力越大,剪胀角越小;法向应力相同时,节理面越粗糙,剪胀角越大。
表5为不同法向应力作用下各人工节理试样对应的峰值剪胀角。采用Boltzmann函数对各组节理在不同法向应力下的峰值剪胀角进行分析,进而得出初始剪胀角。Boltzmann函数的表达式为:
{i_{\rm p}} = {A_2} + \frac{{{A_1} - {A_2}}}{{1 + \exp \left\{ {{{\left( {{{{x}}_\sigma } - {{{x}}_{{\sigma _0}}}} \right)} / {{d_{{x_\sigma }}}}}} \right\}}} (6) 式中:
{A_1} 、{A_2} 为函数的最终值和初始值;{{{x}}_{{\sigma _0}}} 为作用的法向应力;{d_{{x_\sigma }}} 为曲线坡度。表 5 各组人工节理的峰值剪胀角Table 5. Peak dilatancy angle of artificial joints in each group法向应力 {\mathrm{\sigma }}_{\mathrm{n}} /MPa 峰值剪胀角/(°) K-I K-II K-III 0.5 15.02 22.23 30.26 1.0 12.26 17.86 25.86 1.5 11.22 15.23 22.61 2.0 9.92 14.73 20.01 3.0 7.94 11.66 17.47 通过Boltzmann函数分析得到K-I、K-II、K-III的初始剪胀角分别为17.71°、27.91°、35.13°。
对式(3)在0~
\theta _{\rm max }^{\rm{*}} 使用积分中值定理可得到平均接触面积比{A_{\rm ave}} ,如下式所示:{A_{\rm ave}} = \dfrac{{\displaystyle\int_0^{\theta _{\max }^*} {{A_0}{{\left( {\dfrac{{\theta _{\max }^ * - {\theta ^ * }}}{{\theta _{\max }^ * }}} \right)}^c}{\rm d}{\theta ^ * }} }}{{\theta _{\max }^ * - 0}} = \dfrac{{{A_0}}}{{C + 1}} (7) K-I、K-II、K-III三组人工节理的初始剪胀角与节理平均接触面积比
{A_{\rm ave}} = {{{A_0}} / {\left( {C + 1} \right)}} 以及最大视倾角\theta _{\rm max }^ * 三者可采用式(8)所示的线性函数表示。在剪切方向固定的情况下,初始剪胀角的大小仅取决于节理面的形貌特征。{i_0} = 7\frac{{{A_0}\theta _{\max }^*}}{{C + 1}}\qquad\qquad\qquad\qquad\qquad\;\;\; (8) 通过人工节理的剪切试验可知,节理剪切时抗剪强度随着节理强度比的增大而增大。在低法向应力情况下,引入节理强度比调整剪胀角影响系数为
f\left( {{\sigma _{{\rm n}}},{\xi _{\sigma _{{\rm c}}}}} \right) ,节理剪切的摩尔-库仑准则可以改进为:{\tau _{{\rm p}}} = {\sigma _{{\rm n}}} \cdot \tan \left( {{\varphi _{{\rm b}}} + 7\frac{{{A_0}\theta _{\max }^*}}{{C + 1}}f\left( {{\sigma _{{\rm n}}},{\xi _{\sigma {{\rm _c}}}}} \right)} \right) (9) Maksimović[36]的研究中采用法向应力和中位角压力值的比值(
{{{\sigma _{{\rm n}}}} / {{P_{\rm N}}}} )来描述影响系数f\left( {{\sigma _{{\rm n}}}} \right) :f\left( {{\sigma _{{\rm n}}}} \right) = \frac{1}{{1 + {{{\sigma _{{\rm n}}}} / {{P_{\rm N}}}}}}\qquad\qquad\qquad\quad (10) 式中,
{P_{\rm N}} 为中位角压力值。Maksimović认为中位角压力值近似节理抗压强度系数JCS的1/10(
{P_{\rm N}} \approx {{JCS} / {10}} )。本文根据相同节理强度比的节理剪切试验结果将其调整为{{JCS} / {12}} 。但是关于影响系数
f\left( {{\sigma _{{\rm n}}}} \right) 的描述仅适用于节理强度比为1的节理,对于上下盘抗压强度不一致的软-硬节理不具适用性。根据本文不同节理强度比的节理剪切试验结果,采用对节理剪切起控制作用的较软盘抗压强度系数JCScs以及节理强度比{\xi _{\sigma {{\rm _c}}}} 共同表示影响系数如下式所示:f\left( {{\sigma _{{\rm n}}},{\xi _{\sigma {{\rm _c}}}}} \right) = \dfrac{1}{{1 + \dfrac{{12{\sigma _{{\rm n}}}}}{{JC{S_{\rm cs}}\left[ {0.2\ln \left( {{\xi _{\sigma {{\rm _c}}}}} \right) + 1} \right]}}}} (11) 将式(8)和式(11)代入式(4)中,可得含有三维形貌参数及节理强度比的抗剪强度模型式:
{\tau _{\rm p}} = {\sigma _{\rm n}}\tan \left( {{\varphi _{\rm b}} + 7\dfrac{{{A_0}\theta _{\max }^*}}{{C + 1}}\dfrac{1}{{1 + \dfrac{{12{\sigma _{{\rm n}}}}}{{JC{S_{\rm cs}}\left[ {0.2\ln \left( {{\xi _{\sigma _{{\rm c}}}}} \right) + 1} \right]}}}}} \right) (12) 该模型采用三维形貌参数来表示节理的初始剪胀角
7{{{A_0}\theta _{\max }^*} / {\left( {C + 1} \right)}} ,从而反映节理的三维形貌对节理剪切强度的影响。并采用节理强度比建立剪胀角影响系数f\left( {{\sigma _{{\rm n}}},{\xi _{\sigma _{{\rm c}}}}} \right) ,反映剪胀角在节理剪切过程中随法向应力和节理强度比的变化规律。从而使得本文所建立的模型能够适用于计算上、下盘抗压强度不一致的软-硬节理的抗剪强度。3 软-硬节理抗剪强度模型与Barton模型的比较分析
Barton[8]提出的JRC-JCS抗剪强度模型,是目前在岩石工程领域中应用最为广泛的节理抗剪强度估算准则。
{\tau _{{\rm p}}} = {\sigma _{{\rm n}}}\tan \left[ {{\varphi _{{\rm b}}} + JRC{{\lg }}\left( {\frac{{JCS}}{{{\sigma _{{\rm n}}}}}} \right)} \right] (13) Barton和Choubey[10]基于对大量岩石节理的剪切试验,绘制出10条标准粗糙度剖面线用以参照评估JRC的值,其取值范围为0~20。但是该方法的肉眼评估存在人为主观因素,易造成偏差。
为提高Barton模型计算的准确性,本文采用Tse等[11]提出的一阶导数均方根Z2式(14),以及建立的Z2与JRC的函数关系式(15)来量化节理剖面线的形态,从而计算节理剖面的粗糙度。
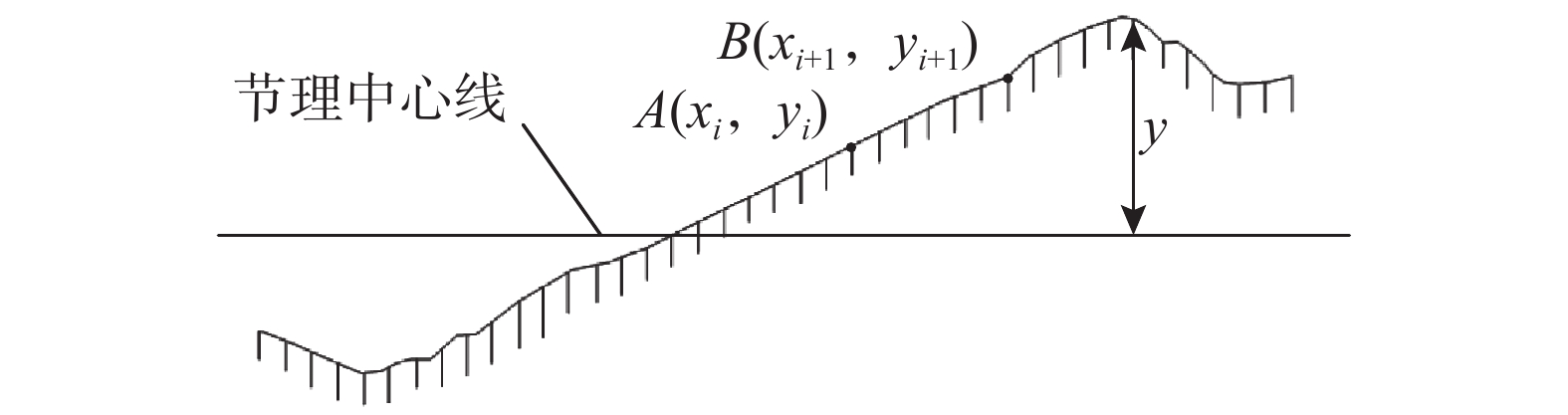
{Z_2} = {\left[ {\frac{1}{L}\int_0^l {{{\left( {\frac{{{\rm d}y}}{{{\rm d}x}}} \right)}^2}} }{\rm{d}}x \right]^{{1 / 2}}}\qquad\quad\quad (14) JRC = 32.2 + 32.47\lg \left( {{Z_2}} \right)\qquad\quad (15) 式中:L为节理轮廓线的长度;y为节理轮廓线的起伏度。
离散化后的一阶导数均方根Z2如式(16)所示。图9为节理粗糙度计算示意图。
{Z_2} = {\left[ {\frac{1}{{m{{\left( {\Delta x} \right)}^2}}}\sum\limits_{i = 1}^{m} {{{\left( {{y_{i + 1}} - {y_i}} \right)}^2}} } \right]^{{1 / 2}}} (16) 式中:
{\varDelta _x} 为采样间距;{\varDelta _y} = {y_{i + 1}} - {y_i} 为两个相邻采样点的起伏差值;m为采样间隔数。节理面抗压强度系数控制着岩体的变形特性和整体稳定,是岩石节理最基本的物理参数。本文采用HT225型回弹仪测量节理面抗压强度系数,按式(17)计算。各组人工节理参数取值见表6。
{\lg }\left( {JCS} \right) = 0.000\;99\gamma {R_{\rm e}} + 1.01 (17) 式中:
\gamma 为岩石的干密度;{R_{\rm e}} 为回弹指数。表 6 Barton模型内各参数Table 6. Parameters in Barton model组号 粗糙度系数JRC 抗压强度系数JCS/MPa 基本摩擦角{\varphi _{\rm b}}/(°) K-I 6.73 19.90 31.0 K-II 11.89 19.90 31.0 K-III 16.41 19.90 31.0 K-III-2 16.41 下盘:19.90 上盘:40.21 31.9 K-III-3 16.41 下盘:19.90 上盘:60.30 32.5 图10为本文模型计算值和Barton模型计算值以及试验值的比较,由图可知:本文模型和节理剪切试验值具有较好的相关性。若采用节理较软盘的抗压强度系数JCScs对Barton模型进行计算,其结果偏小;若采用节理较硬盘的抗压强度系数JCSch对Barton模型进行计算,则计算结果远大于试验值,且平均偏差随着法向应力的增大而不断增大。节理抗剪强度试验值更接近由较软盘抗压强度系数JCScs计算的Barton模型,由此可知剪切过程中节理较软盘抗压强度对节理的剪切强度起控制作用。
按式(18)计算Barton模型和本文模型与试验值的平均偏差。计算结果见表7。
{\sigma _{\rm ave}} = \frac{1}{n}\sum\nolimits_{i = 1}^n {\left| {\frac{{{\tau _{{\rm{pt}}}} - {\tau _{{\rm{pc}}}}}}{{{\tau _{{\rm{pt}}}}}}} \right|} \times 100\text{%} (18) 式中:
{\sigma _{\rm ave}} 为平均偏差;n为试件数;{\tau _{{{\rm pt}}}} 为抗剪强度试验值;{\tau _{{{\rm pc}}}} 为抗剪强度模型计算值。表 7 本文模型和Barton模型的平均偏差Table 7. Average deviation of new model and Barton model/(%) 组号 本文模型 Barton模型 取较软盘抗压强度 取较硬盘抗压强度 K-I 4.0 4.3 K-II 3.5 4.5 K-III 3.4 4.4 K-III-2 3.6 6.9 12.2 K-III-3 3.4 9.8 21.9 Barton模型计算常规的岩石节理抗剪强度具有一定的可靠性[9],但对于节理上、下盘抗压强度不一致的软-硬节理不具普遍适用性。由表7本文模型和Barton模型的平均偏差可知:当节理上、下盘抗压强度相同,即节理强度比
{\xi _{\sigma {{\rm _c}}}} 为1时,本文模型和Barton模型计算结果的准确度均较高,平均偏差都在10%以内,但本文模型的平均偏差略小。当节理上、下盘抗压强度不同,即节理强度比{\xi _{\sigma_ {{\rm c}}}} 大于1时,Barton模型采用较软盘抗压强度进行计算时,平均偏差在10%左右;若采用较硬盘抗压强度进行计算时,平均偏差在10%以上;而本文模型的平均偏差在5%以内。由此证明了Barton模型不适用于软-硬节理的抗剪强度计算,而本文模型对此有较好的可靠性。4 软-硬节理抗剪强度模型的适用性验证
云南某水电站库区内斜坡的后缘出现了深度达10 m的拉裂缝。为揭示该斜坡的失稳机理,以及评估斜坡的安全性系数,某勘测设计研究院在山体打入2个平硐。在一号平硐90 m~95 m洞段内,发现了上、下盘抗压强度不一致的软-硬节理,如图11所示。节理的上盘为长期受高地应力挤压的泥岩,下盘为裂隙较发育的灰岩。考虑到节理的上、下盘抗压强度有较大差别,采用本文提出的软-硬节理抗剪强度模型对该节理的抗剪强度进行计算。
取样时尽量减少扰动,将现场取回的大块、不规则岩样在室内进行切割处理,试样大小控制在10 cm×10 cm左右。将切割好的试样,采用高强水泥砂浆,固定在剪切盒内,制样过程如图12所示。制备完成的试样如图13所示。将剩余的岩样制成各类试样,用以测试节理岩样的各项力学参数,节理试样各项参数的平均值见表8。
采用岩体剪切仪,对养护好的节理试样进行常法向应力下的剪切试验。在试验前通过三维激光扫描仪获取节理面高程信息,计算三维形貌参数,试验结果以及各参数见表9。
通过式(18)对本文模型计算值和试验值的平均偏差进行计算,得到的平均偏差为5.54%。由此可知,本文模型的计算值和试验值较为吻合,证明本文模型能够适用于计算上、下盘抗压强度不一致的软-硬节理的抗剪强度。
表 8 节理材料的基本参数Table 8. Basic parameters of joint materials岩性 抗压强度系数JCS/MPa 弹性模量E/GPa 泊松比\nu /(%) 基本摩擦角{\varphi _{\rm b}}/(°) 强度比{\xi _{\sigma {\rm{_c} } } } 上盘(泥岩) 16.67 2.13 0.35 29.5 4.17 下盘(灰岩) 69.51 5.12 0.25 表 9 节理表面三维参数及试验结果Table 9. Three-dimensional parameters and experimental results of surface试样
名称最大接触
面积比A0粗糙度
参数C最大视
倾角\theta _{\max }^ *法向应力
{\sigma _{\rm{n}}}/MPa剪应力
{\sigma _{{\rm{pt}}} }/MPa本文模型
计算值{\sigma _{\rm{pc}}}/MPa试样
名称最大接触
面积比A0粗糙度
参数C最大视
倾角\theta _{\max }^ *法向应力
{\sigma _{\rm{n}}}/MPa剪应力
{\sigma _{\rm{pt}}}/MPa本文模型
计算值{\sigma _{\rm{pc}}}/MPaC1-1 0.436 5.50 53.6 0.93 1.01 0.96 C4-1 0.467 11.12 57.8 2.37 1.89 1.73 C1-2 0.563 5.40 63.0 0.98 1.46 1.38 C4-2 0.521 9.01 57.2 2.51 2.12 1.97 C1-3 0.460 7.05 72.1 1.01 1.16 1.12 C4-3 0.537 4.93 73.0 2.51 3.14 2.86 C1-4 0.505 11.29 80.8 1.15 1.07 1.10 C4-4 0.481 4.87 62.6 2.71 2.74 2.60 C1-5 0.463 6.69 45.2 1.25 0.99 1.08 C4-5 0.521 7.07 81.0 2.89 2.86 2.74 C2-1 0.556 7.47 61.0 1.35 1.41 1.37 C5-1 0.521 4.98 73.5 3.25 3.12 3.30 C2-2 0.448 5.31 75.7 1.52 1.75 1.80 C5-2 0.507 10.11 66.2 3.26 2.54 2.46 C2-3 0.499 9.69 62.0 1.56 1.45 1.32 C5-3 0.464 6.73 75.5 3.37 3.16 2.88 C2-4 0.441 10.60 69.8 1.59 1.41 1.30 C5-4 0.484 9.57 67.3 3.41 2.51 2.56 C2-5 0.526 5.50 43.5 1.75 1.53 1.57 C5-5 0.480 4.65 73.6 3.61 3.79 3.49 C3-1 0.520 5.92 66.9 1.96 2.14 2.05 C6-1 0.420 7.67 54.1 3.83 2.63 2.71 C3-2 0.536 7.73 60.7 2.01 1.97 1.80 C6-2 0.538 5.75 78.6 4.11 4.13 3.80 C3-3 0.448 4.56 55.4 2.10 2.13 2.02 C6-3 0.475 6.14 68.0 4.26 3.69 3.43 C3-4 0.510 8.43 56.1 2.11 1.84 1.72 C6-4 0.481 9.75 72.7 5.13 3.55 3.64 C3-5 0.489 7.25 80.8 2.19 2.01 2.16 C6-5 0.503 5.36 58.6 5.36 4.24 4.13 5 结论
本文借助三维激光扫描技术和3D打印技术,浇筑了具有自然节理形貌的上下盘抗压强度相同和上下盘抗压强度不同的人工节理试样,并对其进行常法向应力下的剪切试验。以剪胀角和三维形貌参数为基础建立岩石节理抗剪强度模型,通过与Barton模型对比并结合工程实例的应用,得到以下主要结论:
(1)人工节理的剪切试验表明,节理的抗剪强度随节理粗糙度、法向应力及节理强度比的增大而增大;节理的剪胀角随法向应力的增大而减小,随节理粗糙度的增大而增大。节理剪切过程中随法向应力和节理强度比的变化,峰值抗剪强度和法向应力的比值呈非线性变化,可表示为:
{{{\tau _{{\rm p}}}} / {{\sigma _{{\rm n}}}}} = \tan \left( {{\varphi _{{\rm b}}} + {i_0}f\left( {{\sigma _{{\rm n}}},{\xi _{\sigma {{\rm _c}}}}} \right)} \right) 。软-硬节理的剪切过程中,较软盘节理抗压强度对节理的剪切强度起控制作用。(2)通过含有三维形貌参数表示的初始剪胀角
{i_0} 以及含有节理强度比的剪胀角影响系数f\left( {{\sigma _{{\rm n}}},{\xi _{\sigma {{\rm _c}}}}} \right) ,来表征剪胀角在节理剪切过程中的演化规律,从而建立适用于软-硬节理的抗剪强度模型。通过与Barton模型的对比验证了本文模型的可靠性,将该模型应用到工程实践中得到的抗剪强度计算值和试验值的平均偏差仅为5.54%,验证了本文提出的模型对软-硬节理具有良好的适用性。 -
表 1 不同配比水泥砂浆的基本参数
Table 1 Basic parameters of cement mortar with different proportions
强度级别 配合比
水∶灰∶砂单轴抗压强度{\sigma _{\rm{c}}}/MPa 弹性模量 E/GPa 低 1∶2∶5 20.31 4.07 中 1∶2.5∶4 43.25 5.94 高 1∶3∶3 62.53 7.53 表 2 人工节理的基本参数
Table 2 Basic parameters of artificial joints
组别 节理材料强度级别 强度比{\xi _{ {\rm \sigma} {\rm{_c} } } } 基本摩擦角{\varphi _{\rm{b}}}/(°) 上盘 下盘 K-I 低 低 1.00 31.0 K-II 低 低 1.00 K-III 低 低 1.00 K-III-2 低 中 2.13 31.9 K-III-3 低 高 3.08 32.5 表 3 不同粗糙度节理直剪试验结果
Table 3 Direct shear test results of joints with different extents of roughness
法向应力{\sigma _{{\rm n}}}/MPa K-I K-II K-III {\tau _{{\rm p}}}/MPa {{{\tau _{{\rm p}}}} / {{\sigma _{{\rm n}}}}} {\tau _{{\rm p}}}/MPa {{{\tau _{{\rm p}}}} / {{\sigma _{{\rm n}}}}} {\tau _{{\rm p}}}/MPa {{{\tau _{{\rm p}}}} / {{\sigma _{{\rm n}}}}} 0.5 0.52 1.04 0.64 1.28 0.86 1.72 1.0 0.85 0.85 1.02 1.02 1.28 1.28 1.5 1.21 0.81 1.59 1.06 1.83 1.22 2.0 1.56 0.78 1.89 0.95 2.09 1.05 3.0 2.30 0.77 2.52 0.84 2.86 0.95 表 4 不同强度比节理直剪试验结果
Table 4 Direct shear test results of joints with different strength ratios
法向应力 {\mathrm{\sigma }}_{\mathrm{n}} /MPa K-III({\xi _{\sigma _{\rm c}} }=1.00) K-III-2({\xi _{\sigma _{\rm c}} }=2.13) K-III-3({\xi _{\sigma _{\rm c}} }=3.08) {\mathrm{\tau }}_{\mathrm{p}} /MPa {\mathrm{\tau }}_{\mathrm{p}} /MPa {\mathrm{\tau }}_{\mathrm{p}} /MPa 0.5 0.86 0.84 0.96 1.0 1.28 1.51 1.57 1.5 1.83 1.90 2.09 2.0 2.09 2.47 2.51 3.0 2.86 3.19 3.15 表 5 各组人工节理的峰值剪胀角
Table 5 Peak dilatancy angle of artificial joints in each group
法向应力 {\mathrm{\sigma }}_{\mathrm{n}} /MPa 峰值剪胀角/(°) K-I K-II K-III 0.5 15.02 22.23 30.26 1.0 12.26 17.86 25.86 1.5 11.22 15.23 22.61 2.0 9.92 14.73 20.01 3.0 7.94 11.66 17.47 表 6 Barton模型内各参数
Table 6 Parameters in Barton model
组号 粗糙度系数JRC 抗压强度系数JCS/MPa 基本摩擦角{\varphi _{\rm b}}/(°) K-I 6.73 19.90 31.0 K-II 11.89 19.90 31.0 K-III 16.41 19.90 31.0 K-III-2 16.41 下盘:19.90 上盘:40.21 31.9 K-III-3 16.41 下盘:19.90 上盘:60.30 32.5 表 7 本文模型和Barton模型的平均偏差
Table 7 Average deviation of new model and Barton model
/(%) 组号 本文模型 Barton模型 取较软盘抗压强度 取较硬盘抗压强度 K-I 4.0 4.3 K-II 3.5 4.5 K-III 3.4 4.4 K-III-2 3.6 6.9 12.2 K-III-3 3.4 9.8 21.9 表 8 节理材料的基本参数
Table 8 Basic parameters of joint materials
岩性 抗压强度系数JCS/MPa 弹性模量E/GPa 泊松比\nu /(%) 基本摩擦角{\varphi _{\rm b}}/(°) 强度比{\xi _{\sigma {\rm{_c} } } } 上盘(泥岩) 16.67 2.13 0.35 29.5 4.17 下盘(灰岩) 69.51 5.12 0.25 表 9 节理表面三维参数及试验结果
Table 9 Three-dimensional parameters and experimental results of surface
试样
名称最大接触
面积比A0粗糙度
参数C最大视
倾角\theta _{\max }^ *法向应力
{\sigma _{\rm{n}}}/MPa剪应力
{\sigma _{{\rm{pt}}} }/MPa本文模型
计算值{\sigma _{\rm{pc}}}/MPa试样
名称最大接触
面积比A0粗糙度
参数C最大视
倾角\theta _{\max }^ *法向应力
{\sigma _{\rm{n}}}/MPa剪应力
{\sigma _{\rm{pt}}}/MPa本文模型
计算值{\sigma _{\rm{pc}}}/MPaC1-1 0.436 5.50 53.6 0.93 1.01 0.96 C4-1 0.467 11.12 57.8 2.37 1.89 1.73 C1-2 0.563 5.40 63.0 0.98 1.46 1.38 C4-2 0.521 9.01 57.2 2.51 2.12 1.97 C1-3 0.460 7.05 72.1 1.01 1.16 1.12 C4-3 0.537 4.93 73.0 2.51 3.14 2.86 C1-4 0.505 11.29 80.8 1.15 1.07 1.10 C4-4 0.481 4.87 62.6 2.71 2.74 2.60 C1-5 0.463 6.69 45.2 1.25 0.99 1.08 C4-5 0.521 7.07 81.0 2.89 2.86 2.74 C2-1 0.556 7.47 61.0 1.35 1.41 1.37 C5-1 0.521 4.98 73.5 3.25 3.12 3.30 C2-2 0.448 5.31 75.7 1.52 1.75 1.80 C5-2 0.507 10.11 66.2 3.26 2.54 2.46 C2-3 0.499 9.69 62.0 1.56 1.45 1.32 C5-3 0.464 6.73 75.5 3.37 3.16 2.88 C2-4 0.441 10.60 69.8 1.59 1.41 1.30 C5-4 0.484 9.57 67.3 3.41 2.51 2.56 C2-5 0.526 5.50 43.5 1.75 1.53 1.57 C5-5 0.480 4.65 73.6 3.61 3.79 3.49 C3-1 0.520 5.92 66.9 1.96 2.14 2.05 C6-1 0.420 7.67 54.1 3.83 2.63 2.71 C3-2 0.536 7.73 60.7 2.01 1.97 1.80 C6-2 0.538 5.75 78.6 4.11 4.13 3.80 C3-3 0.448 4.56 55.4 2.10 2.13 2.02 C6-3 0.475 6.14 68.0 4.26 3.69 3.43 C3-4 0.510 8.43 56.1 2.11 1.84 1.72 C6-4 0.481 9.75 72.7 5.13 3.55 3.64 C3-5 0.489 7.25 80.8 2.19 2.01 2.16 C6-5 0.503 5.36 58.6 5.36 4.24 4.13 -
[1] Pollard D, Aydin A. Progress in understanding jointing over the past century [J]. Geological Society of America Bulletin, 1988, 100(8): 1181 − 1204.
[2] 夏才初, 孙宗欣. 工程岩体节理力学 [M]. 上海: 同济大学出版社, 2002. Xia Caichu, Sun Zongxin. Joint mechanics of engineering rock mass [M]. Shanghai: Tongji Universtiy Press, 2002. (in Chinese)
[3] Patton F D. Multiple modes of shear failure in rock [C]//Proceedings of the First Congress of International Society of Rock Mechanics. Lisbon: [s. n.], 1966: 509 − 513.
[4] Maksimović M. New description of the shear strength for rock joints [J]. Rock Mechanics and Rock Engineering, 1992, 25(4): 275 − 284.
[5] 肖卫国, 兑关锁, 任青文. 节理岩体非线性本构模型的研究[J]. 工程力学, 2010, 27(9): 1 − 6. Xiao Weiguo, Dui Guansuo, Ren Qingwen. Study of non-linear constitutive model for jointed rock masses [J]. Engineering Mechanics, 2010, 27(9): 1 − 6. (in Chinese)
[6] 尹显俊, 王光纶, 张楚汉. 岩体结构面切向循环加载本构关系研究[J]. 工程力学, 2005, 22(6): 97 − 103. Yin Xianjun, Wang Guanglun, Zhang Chuhan. Study of constitutive model for rock interfaces and joints under cyclic shear loading [J]. Engineering Mechanics, 2005, 22(6): 97 − 103. (in Chinese)
[7] Kulatilake P H S W, Shou G, Huang T H, et al. New peak shear strength criteria for anisotropic rock joints [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1995, 32(7): 673 − 697.
[8] Barton N. Review of a new shear strength criterion for rock joints [J]. Engineering Geology, 1973, 7(4): 287 − 332.
[9] Wei Y F, Fu W X, Nie D X. Nonlinearity of the rock joint shear strength [J]. Strength of Materials, 2015, 47(1): 205 − 212. doi: 10.1007/s11223-015-9649-8
[10] Barton N, Choubey V. The shear strength of rock joints in theory and practice [J]. Rock Mechanics, 1977, 10(1/2): 1 − 54.
[11] Tse R, Cruden D M. Estimating joint roughness coefficients [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1979, 16(5): 303 − 307.
[12] Zhang G C, Karakus M, Tang H M, et al. A new method estimating the 2D joint roughness coefficient for discontinuity surfaces in rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 72: 191 − 198.
[13] Yang Z Y, Lo S C, Di C C. Reassessing the joint roughness coefficient estimation using Z2 [J]. Rock Mechanics and Rock Engineering, 2001, 34(3): 243 − 251.
[14] Yu X B, Vayssade B. Joint profiles and their roughness parameters [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1991, 28(4): 333 − 336.
[15] Belem T, Homand F, Souley M. Quantitative parameters for rock joint surface roughness [J]. Rock Mechanics and Rock Engineering, 2000, 33(4): 217 − 242.
[16] Ei-Soudani S M. Profilometric analysis of fractures [J]. Metallography, 1978, 11(3): 247 − 336.
[17] Grasselli G, Wirth J, Egger P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing [J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(6): 789 − 800.
[18] Grasselli G, Egger P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters [J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 25 − 40.
[19] Grasselli G. Manuel rocha medal recipient shear strength of rock joints based on quantified surface description [J]. Rock Mechanics and Rock Engineering, 2006, 39(4): 295 − 314.
[20] Xia C C, Tang Z C, Xiao W M, et al. New peak shear strength criterion of rock joints based on quantified surface description [J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 387 − 400.
[21] Yang J, Rong G, Hou D, et al. Experimental study on peak shear strength criterion for rock joints [J]. Rock Mechanics and Rock Engineering, 2016, 49(3): 821 − 835.
[22] Tang Zhicheng, Liu Quansheng, Huang Jihui. New criterion for rock joints based on three-dimensional roughness parameters [J]. Journal of Central South University, 2014, 21(12): 4653 − 4659.
[23] 唐志成, 夏才初, 宋英龙, 等. Grasselli节理峰值抗剪强度公式再探[J]. 岩石力学与工程学报, 2012, 31(2): 356 − 364. Tang Zhicheng, Xia Caichu, Song Yinglong, et al. Discussion about Grasselli’s peak shear strength criterion for rock joints [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 356 − 364. (in Chinese)
[24] 杨洁, 荣冠, 程龙, 等. 节理峰值抗剪强度试验研究[J]. 岩石力学与工程学报, 2015, 34(5): 884 − 894. Yang Jie, Rong Guan, Cheng Long, et al. Experimental study of peak shear strength of rock joints [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 884 − 894. (in Chinese)
[25] Nasir O, Fall M. Shear behaviour of cemented paste fill rock interfaces [J]. Engineering Geology, 2008, 101(3/4): 146 − 153.
[26] Wu Q, Xu Y, Tang H, et al. Peak shear strength prediction for discontinuities between two different rock types using a neural network approach [J]. Bulletin of Engineering Geology and the Environment, 2019, 78(4): 2315 − 2329.
[27] Ghazvinian A H, Taghichian A, Hashemi M, et al. The shear behavior of bedding planes of weakness between two different rock types with high strength difference [J]. Rock Mechanics and Rock Engineering, 2010, 43(1): 69 − 87.
[28] 宋磊博, 江权, 李元辉, 等. 软-硬自然节理的改进JRC-JCS剪切强度公式[J]. 岩土力学, 2017, 38(10): 2789 − 2798. Song Leibo, Jiang Quan, Li Yuanhui, et al. Improved JRC-JCS shear strength formula for soft-hard natural joints [J]. Rock and Soil Mechanics, 2017, 38(10): 2789 − 2798. (in Chinese)
[29] 陈世江, 朱万成, 王创业, 等. 岩体结构面粗糙度系数定量表征研究进展[J]. 力学学报, 2017, 49(2): 239 − 256. Chen Shijiang, Zhu Wancheng, Wang Chuangye, et al. Review of research progresses of the quantifying joint roughness coefficient1 [J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 239 − 256. (in Chinese)
[30] 陈蕴生, 李宁, 李爱国, 等. 非贯通节理介质细观损伤演化的CT分析[J]. 岩石力学与工程学报, 2000, 19(6): 702 − 706. Chen Yunsheng, Li Ning, Li Aiguo, et al. Analysis on meso-damage process of non-interpenetraed jointed media by using CT [J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(6): 702 − 706. (in Chinese)
[31] Jiang Q, Feng X, Gong Y, et al. Reverse modelling of natural rock joints using 3D scanning and 3D printing [J]. Computers and Geotechnics, 2016, 73(5): 210 − 220.
[32] Head D, Vanorio T. Effects of changes in rock microstructures on permeability: 3-D printing investigation [J]. Geophysical Research Letters, 2016, 43(14): 7494 − 7502. doi: 10.1002/2016GL069334
[33] 肖维民, 黄巍, 丁蜜, 等. 基于3D打印技术的模拟柱状节理岩体试样制备方法[J]. 岩土工程学报, 2018, 40(增刊 2): 256 − 260. Xiao Weimin, Hunag Wei, Ding Mi, et al. Method for preparing artificial columnar jointed rock mass specimens by using 3D printing technology [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(Suppl 2): 256 − 260. (in Chinese)
[34] 刘泉声, 何璠, 邓鹏海, 等. 3D打印技术在岩石物理力学试验中的应用[J]. 岩土力学, 2019, 40(9): 3397 − 3404. Liu Quansheng, He Pan, Deng Penghai, et al. Application of 3Dprinting technology in physical modelling in rock mechanics [J]. Rock and Soil Mechanics, 2019, 40(9): 3397 − 3404. (in Chinese)
[35] Hopkins D L. The implication of joint deformation in analyzing the properties and behavior of fractured rock masses, under-ground excavations, and faults [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1): 175 − 202. doi: 10.1016/S1365-1609(99)00100-8
[36] Maksimović M. The shear strength components of a rough rock joint [J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts, 1996, 33(8): 769 − 783. doi: 10.1016/0148-9062(95)00005-4




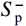
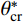
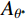
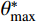
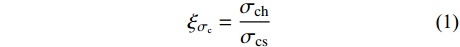
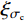
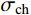
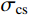

 下载:
下载: