工程结构服役期内会受到各类随机动力作用^[1]，结构响应也表现出明显的随机性。开展随机动力作用下的结构可靠度分析对结构性能和安全性评估至关重要。近年来，由李杰和陈建兵^[2-3]提出的广义概率密度演化理论(Generalized probability density evolution theory, GPDET)为结构的随机响应预测及其可靠度分析提供了新的途径。

由于实际工程的复杂性，GPDET的偏微分方程很难获得精确理论解析解，因此常采用数值方法求解^[4]。这些数值算法包括有限元法^[5]、路径积分法^[6]、等效线性化法^[7]、有限差分法^[8]等。当采用适当的差分格式时，有限差分法在概率密度演化分析中表现出良好性能^[9]。目前常用的概率密度演化方程(PDEE)有限差分法按照差分近似微分的处理方式分为单边差分、L-W双边差分和总变差减小(TVD)性质差分^[10]三种数值差分方法。单边差分和L-W双边差分法分别利用单向差分和中心差分来近似微分结果，两者分别具有一阶和二阶计算精度。而TVD差分法由于引入了通量限制器，避免了L-W双边差分法可能存在的非物理负数概率解。因此，李杰和陈建兵^[10]构造了一类适用于PDEE求解的TVD差分格式并将其沿用于其后开展的各项概率密度演化分析。

GPDET分为概率分配和PDEE求解两大关键步骤。概率分配对计算精度影响的研究^[11-12]已较为成熟。在概率分配满足计算精度的前提下，YU等^[13]基于GPDET开展铁路桥梁在随机荷载条件下的结构响应分析时，通过对比数论选点法与蒙特卡洛法的激励样本计算结果，验证了车轨桥随机振动模型的正确性；XU等^[14]基于GPDET将车辆—轨道相互作用模型与轨道不平顺概率模型有效耦合，同样利用数论选点法与蒙特卡洛法计算结果对比，验证了耦合模型的正确性。以往研究中，GPDET与蒙特卡洛法的对比结果仅体现了概率分配步骤中代表性样本对样本空间的表征性，而两种方法对比的均值和标准差均采用TVD差分法计算。由于该差分方法计算精度有限，且在局部极值点附近精度降低^[15]，这也导致概率密度演化分析中^[16-17]，在荷载作用的后半程(卸载阶段)，结构响应的概率密度演化标准差结果依旧持续增大，这样的计算结果显然不满足精度要求，甚至不符合实际情况。因此，PDEE求解步骤中产生的计算误差不容忽视，开展基于TVD差分法的PDEE数值求解精度分析非常重要。

通常情况下，PDEE的初值条件为在空间方向可导性较差的脉冲型狄拉克(Dirac)函数，这将影响到概率密度数值解和可靠度分析的精确性。为提升TVD差分方法的求解精度，石晟等^[18]提出了余弦型初值条件，余弦型初值虽比脉冲型初值平滑，但空间方向的初始概率赋值范围受限于余弦函数周期，且未给出时间差分步长选取原则。

本文针对PDEE，首先对单边差分、L-W双边差分和TVD差分三种差分方法开展单样本和多样本的差分精度分析；进而提出了TVD差分的时间步长合理选取方法和正态分布型初值条件，通过与蒙特卡洛法的数理统计均值和方差作对比，验证了本文方法的合理性。

1   概率密度演化方程及数值求解方法

1.1   概率密度演化方程

结构响应量${\boldsymbol{Z}}$和随机变量${\boldsymbol{\varTheta}}$组成的增广系统$({\boldsymbol{Z}},{\boldsymbol{\varTheta}} )$是一个保守的随机系统，随机性完全来自于${\boldsymbol{ \varTheta}}$，整个过程中，没有随机因素的增减。将$({\boldsymbol{Z}},{\boldsymbol{\varTheta}} )$的联合概率密度函数记为${p_{{\boldsymbol{Z}},{\boldsymbol{\theta}} }}({\boldsymbol{Z}},{{\boldsymbol{\theta }}},t)$，根据概率守恒原理^[19]，对于给定的离散参数代表点集${{\boldsymbol{\theta}} _l}$($l = 1,2,\cdots ,{n_{{\rm{sel}}}}$)，PDEE可写为一维偏微分方程形式：

第$l$组离散代表点集对应的边界条件和初始条件为：

式中：$\delta$为Dirac函数；${P_l}$为初始赋得概率；${Z_0}$为初始时刻对应的结构响应量。

对${n_{{\rm{sel}}}}$组概率密度分布值${p_{{{Z}},{\boldsymbol{\varTheta}}} }(Z,{{\boldsymbol{\theta}} _l},t)$进行累计求和，得到最终的结构响应数值解：

按照GPDET计算均值$\mu$与标准差$\sigma$：

式中：${\rm{d}}{\textit{z}}$为空间离散步长；$n{\textit{z}}$为空间离散点数量。

1.2   数值求解方法

式(1)的偏微分方程很难给出理论解析解，故通常采用数值差分方法进行求解计算。通过对概率密度值$p$进行时间$t$方向的一阶和二阶泰勒展开^[9]，利用差分方法近似$p$的一阶和二阶偏微分，可得：

式中：$p_j^k$为第$j$个空间步在第$k$个时间点对应的概率密度；$\Delta t$和$\Delta Z$分别为时间间隔和空间响应间隔。

在微小时间间隔[$t$, $t + \Delta t$]内，加速度$\ddot Z \approx 0$，故略去加速度项$\ddot Z$，利用式(5)和式(6)，经整理可得到式(7)所示的单边差分格式和式(8)所示的L-W双边差分格式(下文简称为双边差分)：

式中：$\lambda$为网格差分比；$\Delta p$为概率密度差值。

单边或双边差分法的概率密度值$p_j^{k + 1}$可由第$k$个时刻各空间步对应的概率密度值线性叠加得到，故可将单边或双边差分法改写为：

式中，${A_\gamma }$为第$k$个时间点对应的线性算子。

单边差分法线性算子为：

双边差分法线性算子为：

由于双边差分法在泰勒展开时忽略了高阶量，导致计算结果产生数值振荡，甚至出现非物理的概率密度负值。为解决这一问题，采用带有通量限制器$\varphi$的TVD性质双边差分格式(简称TVD差分)，以此来限制数值通量恒为正数：

式中，$\varphi$为通量限制器，取值范围为[0, 1]，具体表达式详见文献[10]。当$\varphi$恒为0，式(14)转化为单边差分法；当$\varphi$恒为1，式(14)转化为双边差分法^[9]。

1.3   差分格式的数值耗散

为比较差分格式的数值耗散情况，通过观察PDEE中初始概率值为谐波函数${{\rm{e}}^{{\rm{i}}\beta Z}}$的传播，来了解差分格式的特征，谐波函数初值条件为：

式中：$\beta$为波数；$\Delta {\textit{z}}$为空间离散步长。

将式(15)代入式(11)可得：

式中，$B$为概率密度演化算子，其大小由网格差分比$\lambda$和结构响应一阶时间导数$\dot Z$确定。当$| B | \leqslant 1$时，式(16)为稳定差分格式^[9]。

通过对式(16)进行迭代便可得到任一时刻的概率值$p_j^{k + 1}$：

式中，${B^{k + 1}}$的上标$k + 1$为对初始概率$p_j^0$进行了$k + 1$次差分迭代计算，而不是对算子$B$进行简单的幂计算。

由于式(5)和式(6)利用差分代替微分得到线性算子${A_\gamma }$，由式(17)可知，差分格式、结构响应方向上各时刻概率密度函数$p$的可导性、结构响应一阶时间导数$\dot Z$、差分求解次数$k$(或时间长短)和概率初值条件${p^0}$均对数值差分结果有直接影响。且任一时刻的概率密度值都可由初值条件$p_j^0$迭代获得。

整理得到单边差分与双边差分概率密度演化算子${B_{{\rm{o}}}}$和${B_{{\rm{d}}}}$的表达式分别为：

当$| {\lambda \dot Z}| < 1$时，双边差分的概率密度演化算子${B_{{\rm{d}}}}$比单边差分的${B_{{\rm{o}}}}$更接近1。由式(18)可知，只考虑一阶泰勒展开的单边差分法，其数值耗散大于考虑二阶泰勒展开项的双边差分法。结合式(14)可知，TVD差分法的数值耗散情况介于单边差分与双边差分之间。

2   数值差分时间步长及正态分布型初值条件

2.1   时间步长选取

数值差分的稳定性条件为CFL条件(Courant-Friedrichs-Lewy condition)：

由式(9)和式(19)可得空间离散步长的要求为：

式(20)表明：只要响应离散步长${\rm{d}}Z$足够大，便可保证概率密度演化计算收敛。而当工程结构受地震^[20]、轨道不平顺^[21]和风载荷^[22]等剧烈变化的随机荷载时，则需要更小的时间步长与空间步长来提升概率密度演化结果计算精度。为呈现出概率密度演化结果的峰值变化，并保证结果误差符合工程要求，必须使各样本的概率演化曲线在“时间—空间”网格上有明显的重叠和分离部分，这就对网格离散精度提出了要求。

有限差分法求解过程示意图如图1所示，竖轴代表响应量，样本A和样本B分别代表样本空间中某两条以通量速度为${\dot Z_{\rm{A}}}$和${\dot Z_{\rm{B}}}$在“时间t—空间Z”网格上进行概率密度演化的曲线。

图  1  有限差分法求解过程示意图

Figure  1.  Finite difference method solution process diagram

下载: 全尺寸图片 幻灯片

图1中，区域1的两样本差异小于${\rm{d}}Z$，两样本的概率密度值将在同一空间离散步左右相邻网格节点上表征，致使两样本结果差异性较低，随着类似情况的增加，误差不断累积，最终的概率密度分布范围也将比实际情况更宽(标准差结果失真)。同时，由于概率守恒(各时刻概率之和恒为1)，概率密度峰值也将比实际情况更小。因此，只有当空间离散步长${\rm{d}}Z$较小时，各样本的变化差异性才能很好的体现出来(如区域2)。

使用TVD差分法求解PDEE时，由于通量限制器$\varphi$取值范围为[0, 1]，故TVD差分法的单样本概率密度演化曲线的离散性只能随差分迭代次数的增加逐渐增大或维持离散性不变，这也将导致最终的概率密度演化结果(或标准差结果)误差较大，甚至是错误的。

为保证数值差分计算精度，体现出各样本之间的差异性，本文提出空间步长${\rm{d}}Z$的最大限值：

式中：$| {\hat Z}|$为关注时间段的各样本结构响应差值范围；$T$为结构响应分析总时长。

为同时满足计算稳定性与精度要求，改进时间步长${\rm{d}}{t^*}$应为：

式中：$T$为概率密度演化分析总时长；$\varPsi$为保守系数，各样本响应结果差异越小，保守系数取值越大。

2.2   正态分布型初值条件

在评价可靠度时，通常将获得关注量的响应与规定限值比较，令“$W$=规定限值$-$关注量响应”。通过假设等价极值事件$W\sin (t)$，将该虚拟三角函数的一阶时程导数$W\cos (t)$代入式(1)，即可得到虚拟随机过程的概率密度演化结果。当$t = \pi /2$时，等价极值事件与实际过程$W$相等^[23]。

基于这一思想，即可得到结构可靠度$R$：

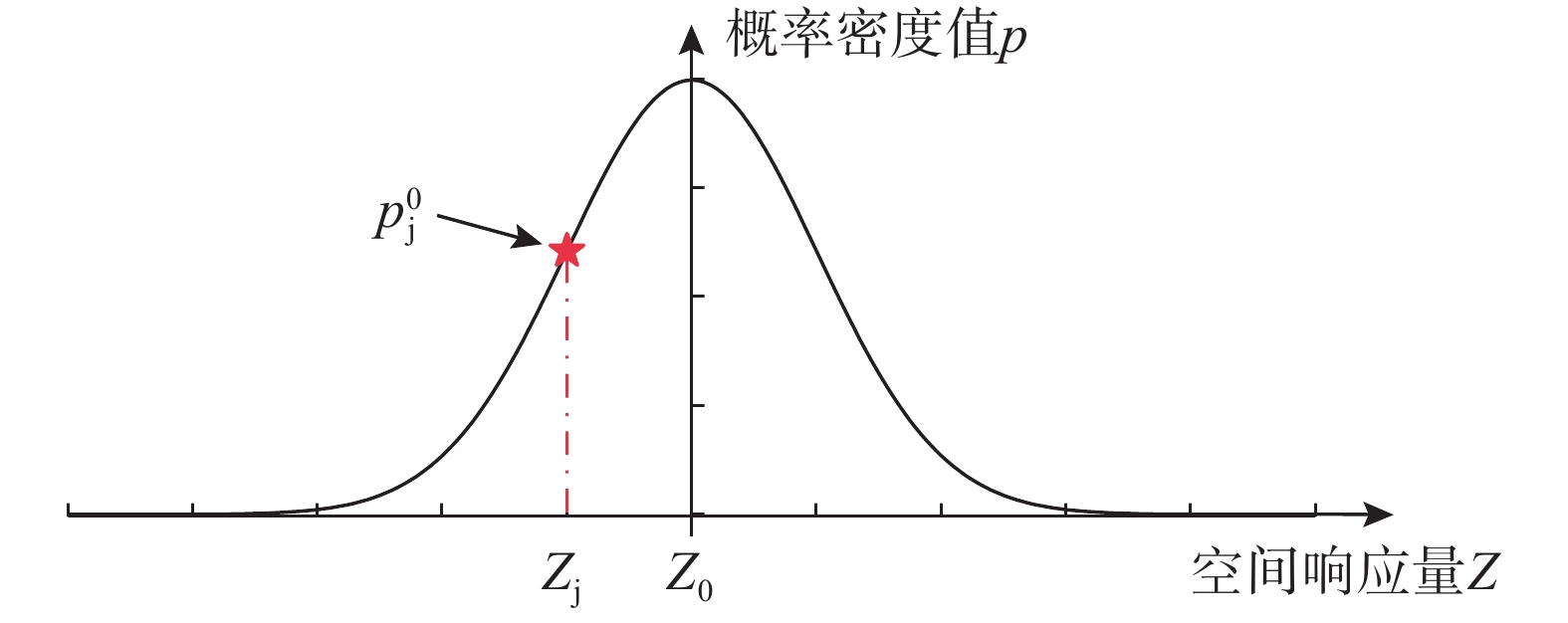
由式(23)可知，概率密度${p_Z}$的求解精度会直接影响后续的可靠度分析结果，通常各样本对应的PDEE初始条件为式(3)所示的${Z_0}$处的脉冲型Dirac函数，而Dirac函数初值条件在空间方向振荡明显，这导致初值条件关于空间方向的可导性对数值计算结果产生影响^[18]。

为进一步提高TVD差分的计算精度，本文基于正态分布函数提出了一种如图2所示的初值条件：

式中：$p_j^0$为在空间离散点${Z_j}$处由正态分布函数N(${Z_0}$, $\sigma$)得到的概率密度值；${Z_0}$为初始时刻虚拟随机过程对应的解。

图  2  基于正态分布函数的初值条件

Figure  2.  Initial condition based on normal distribution function

下载: 全尺寸图片 幻灯片

为满足概率守恒条件，需使初始时刻各空间离散点的概率之和为1，则修正后的概率密度$\hat p_j^0$为：

式中，$nj$为空间离散点数量。

正态分布函数型初值条件的概率峰值及分布范围受标准差$\sigma$控制。当$\sigma$取值较小(即初值条件集中在${Z_0}$处)时，该分布条件可近似于脉冲型Dirac函数初值分布。

3   差分格式计算精度的影响因素

3.1   样本精度影响分析

3.1.1   单样本数值差分精度

为对比不同差分格式对结构可靠度计算精度的影响，构造目标三角函数$y(t)$：

式中：$A$为三角函数幅值，取值为2；$t$为时间，选取范围为0 s~3.15 s。

选取差分时间步长0.0001 s，按式(4)计算单样本的均值和标准差(该统计特征值无实际物理意义，仅用于判断演化结果的离散程度)，结果见图3。

图  3  不同差分格式的单样本离散程度

Figure  3.  The degree of single sample dispersion of different difference schemes

下载: 全尺寸图片 幻灯片

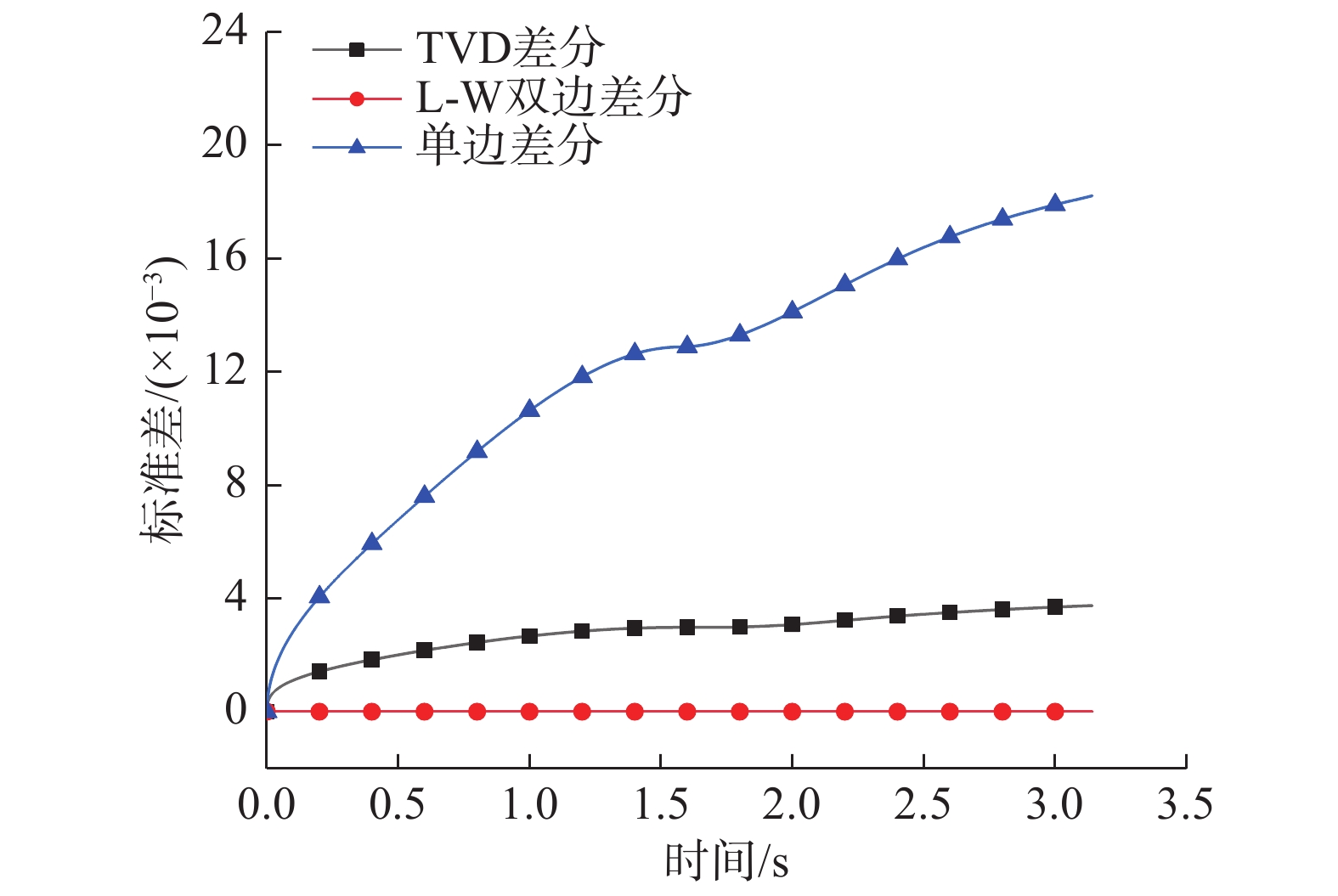
图3中：三种差分格式计算的单样本标准差均随着时间增大而增大(其中双边差分结果过小而不明显)，这是由于随着差分迭代次数的增加，数值耗散越来越严重。其中，双边差分格式的数值耗散问题最小，单样本标准差都远小于其他差分格式。0.0001 s差分时间步长下，双边差分格式在$\pi$时刻的标准差为$2.5\times {10}^{-10}$；而单边差分法单样本离散程度最严重，不建议工程使用，下文将不再对单边差分法进行计算分析。

图4为0.01 s~0.0001 s内不同差分时间步长的单样本均值结果。由图4可知，0.01 s的时间步长即可满足目标函数“确定性分析计算要求”。各差分时间步长下单样本均值结果一致，差分方法以及差分步长对均值结果的不产生影响。

图  4  不同差分时间步长的单样本均值

Figure  4.  Single sample means with different difference time steps

下载: 全尺寸图片 幻灯片

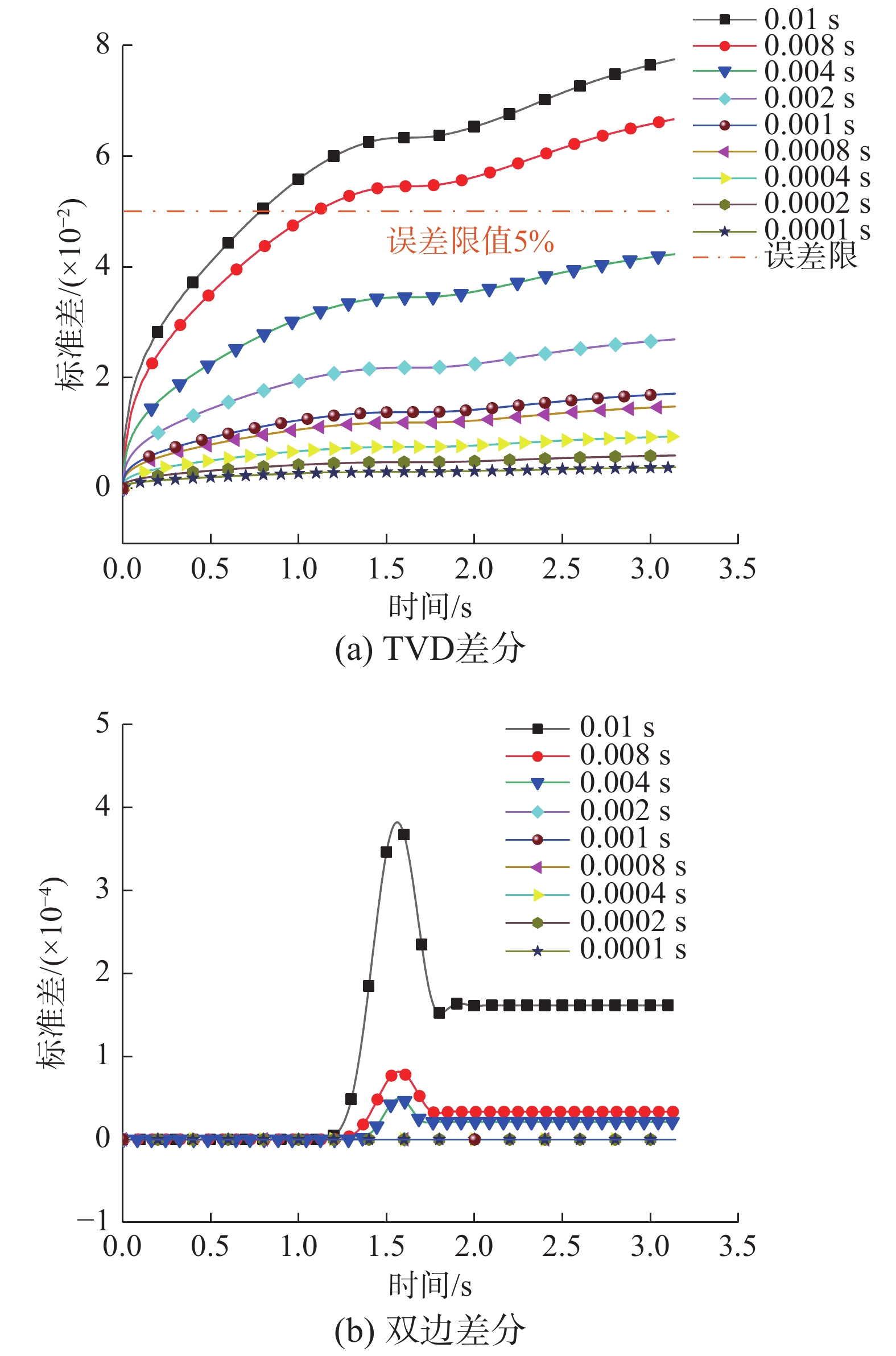
图5为TVD差分和双边差分格式不同差分步长的单样本离散程度。由图5(a)可知，0.01 s和0.0001 s差分时间步长在$\pi$时刻对应的TVD差分标准差分别为0.0774和0.0037，仅满足确定性分析计算要求(0.01 s)的概率结果离散性明显大于0.0001 s的标准差结果。当差分步长小于0.004 s时，TVD差分在第一个周期内的标准差均小于5%。按式(22)计算的时间步长为${\rm{d}}{t^*} \leqslant 0.05/(5\times2\times5) = 0.001\;{\rm{s}}$，该步长能很好地保证TVD差分的单样本计算精度。图5(b)中，双边差分标准差均符合误差限值要求，这表明相同误差限值要求下，双边差分可采用更大的差分步长，提升计算效率。

图  5  不同差分时间步长的单样本标准差

Figure  5.  Single sample standard deviations with different difference time steps

下载: 全尺寸图片 幻灯片

3.1.2   多样本数值差分精度

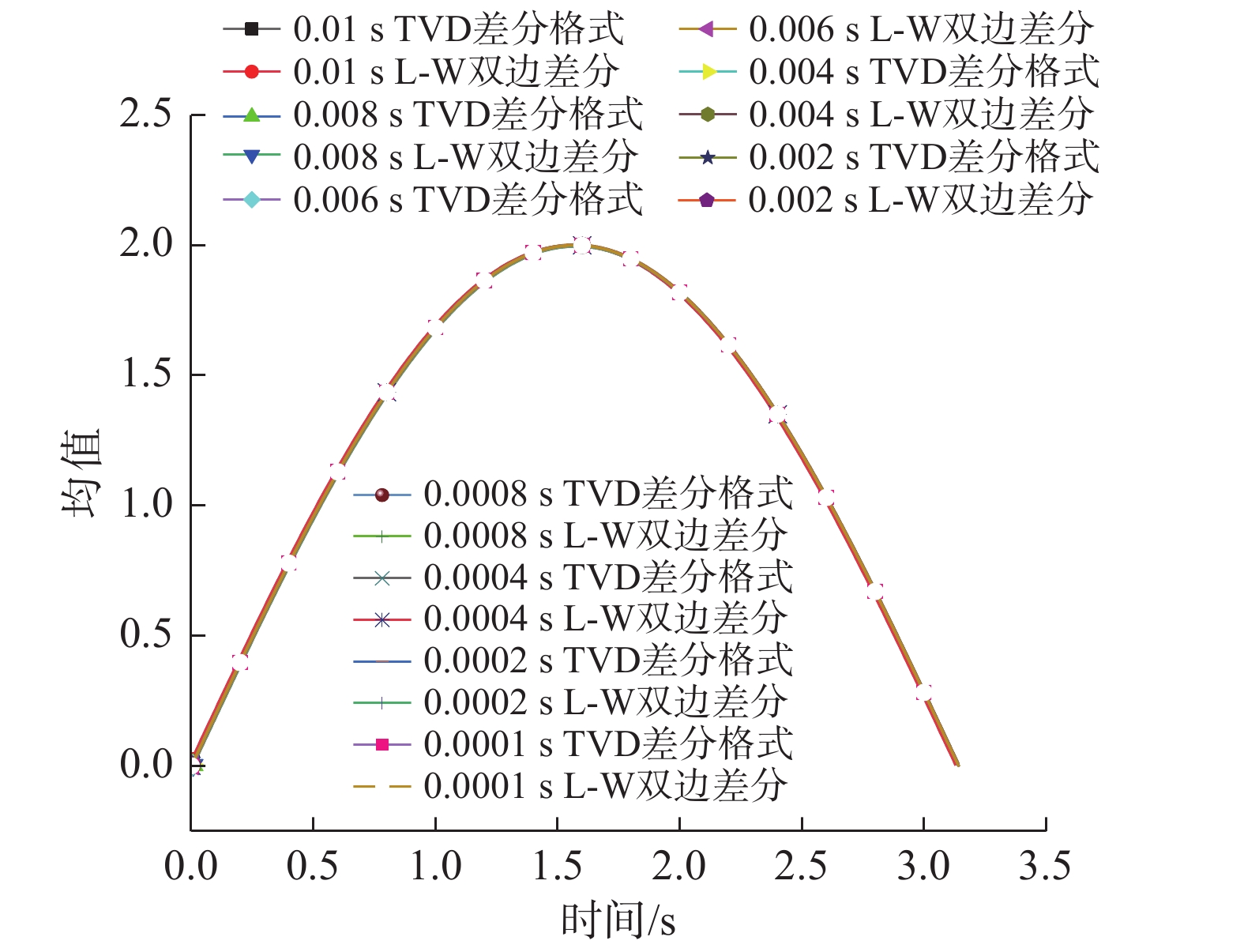
为进一步验证式(22)的时间步长选取的合理性，假定式(26)的三角函数幅值$A$为服从正态分布N(2, 0.1)，并对100条随机正弦曲线开展概率密度演化计算，验证本文时间步长选取方法的合理性。满足式(22)的差分时间步长为${\rm{d}}{t^*} \leqslant \dfrac{{0.04}}{{5\times2\times5}} = 0.0008\;{\rm{s}}$。

图6为不同差分时间步长的多样本统计特征值。图6(a)中，差分时间步长对多样本均值不产生影响。图6(b)中，TVD差分的标准差结果受差分时间步长影响显著，0.0008 s和0.01 s时间步长的$\pi /2$时刻处标准差值分别为0.098 56和0.1147，与精确解0.1的误差分别为1.44%和14.7%，随着概率的演化，各差分时间步长的标准差相对于精确解均出现了增大现象，其中$\pi$时刻精确解为0，而0.01 s步长计算的标准差为0.071 22，计算结果严重偏离精确解。图6(c)中，由于双边差分的单样本的数值耗散远小于TVD差分，故其多样本标准差结果也更接近于精确解。双边差分法以0.0008 s和0.01 s时间步长计算的$\pi /2$时刻处标准差值分别为0.099 69和0.0987，与精确解0.1的误差分别为0.31%和1.3%。因此，当计算结果仅关注均值和标准差等统计指标时，使用数值耗散较小的双边差分法，可在较大步长条件下获得高精度的统计指标，并大幅缩减计算时间。

图  6  不同差分时间步长的多样本统计特征值

Figure  6.  Multiple statistical eigenvalues of different difference time steps

下载: 全尺寸图片 幻灯片

3.2   改进初值条件

第3.1节中目标函数$y(t)$的一阶时间导数值相较于函数自身的大小差异不明显。为进一步考察初值条件及其可导性对TVD差分的影响，构造一阶时间导数值较大且空间方向可导性较差的目标概率密度函数$Y(A,t)$作为精确解：

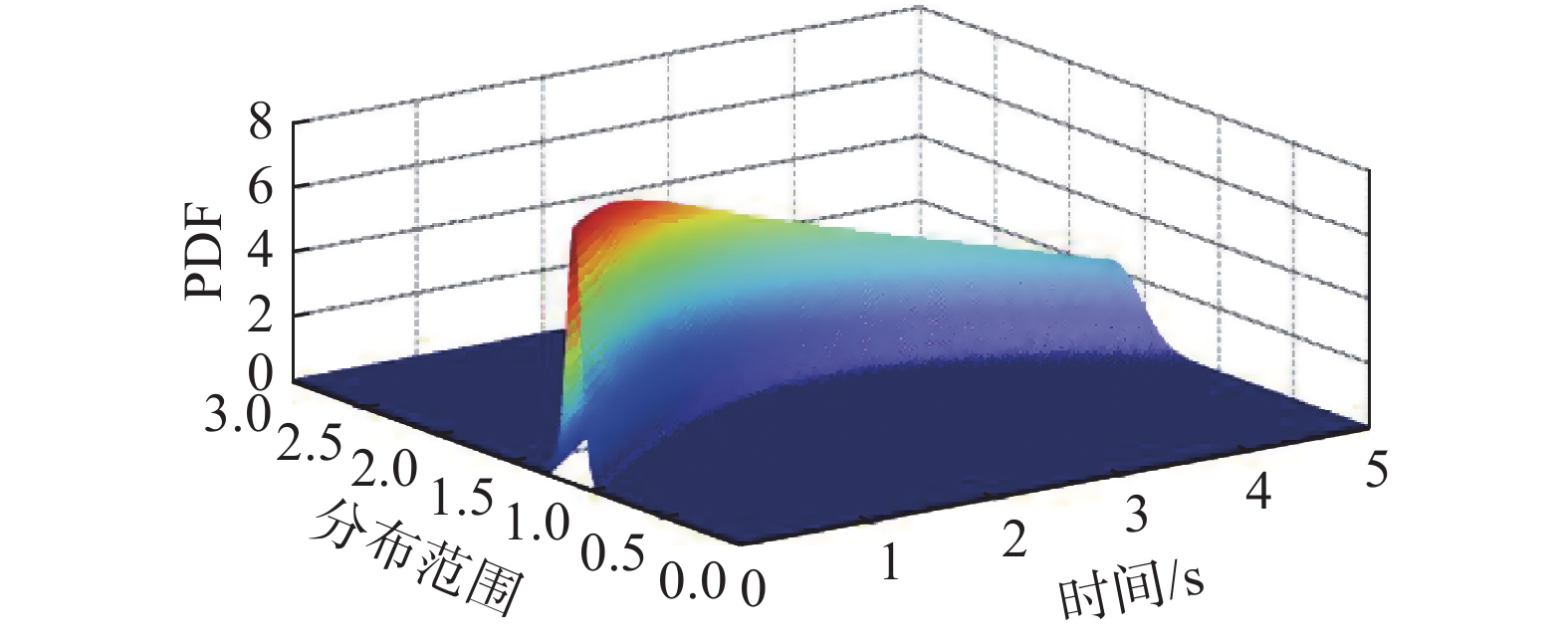
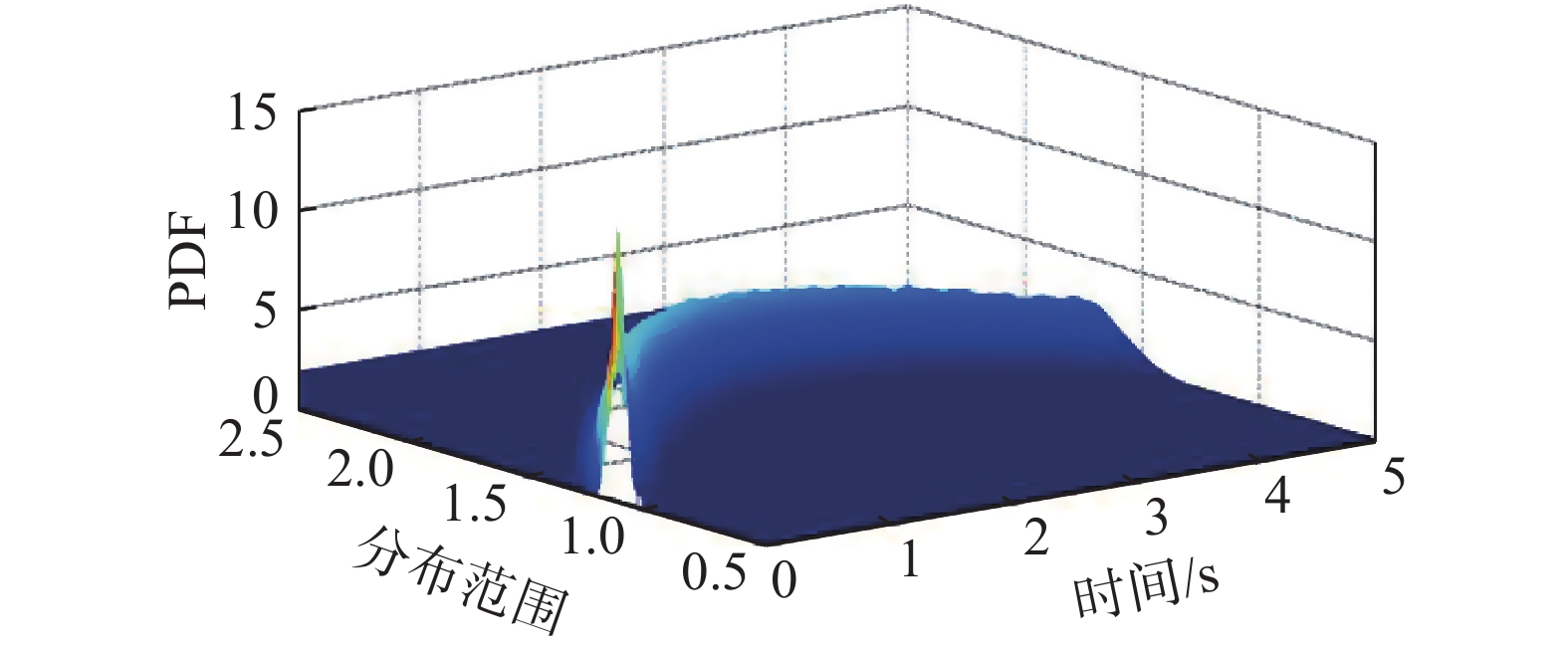
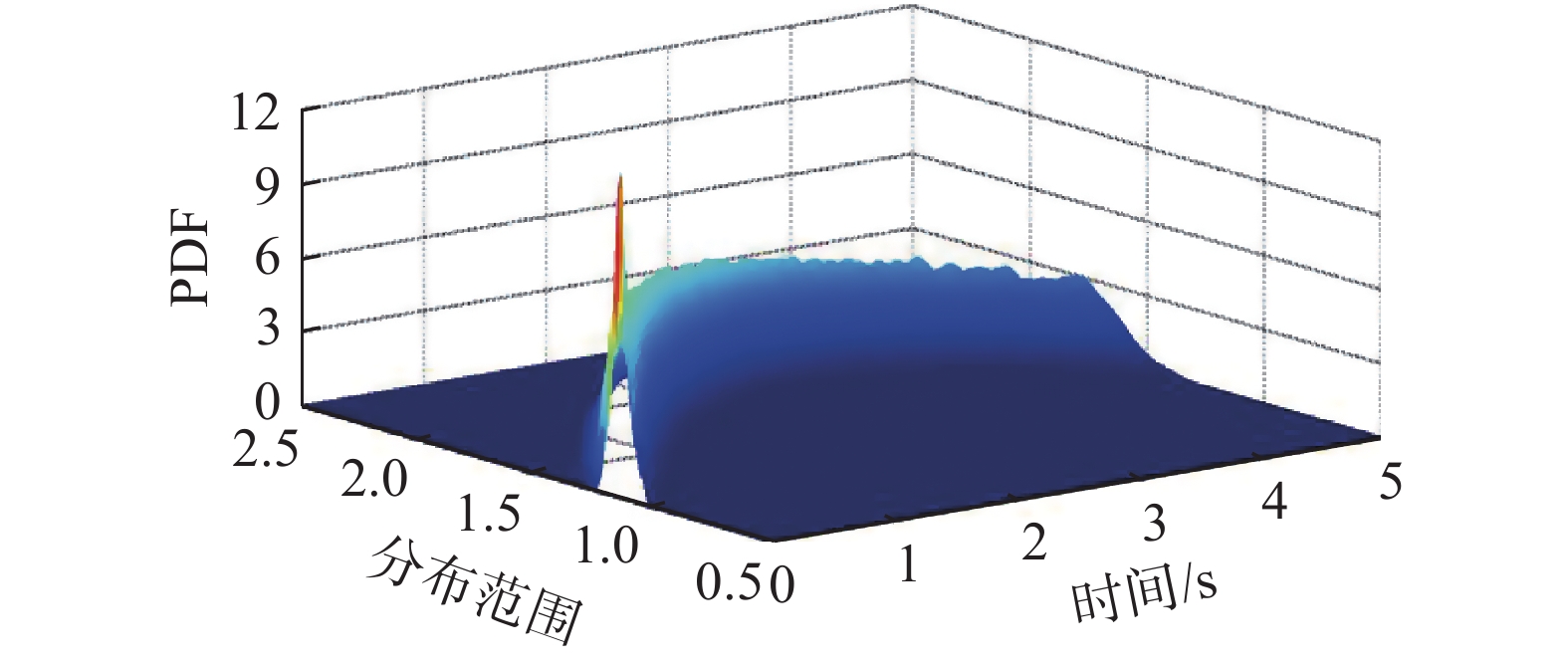
式中：$A$为在任一时刻$t$服从随机特定正态分布的变量，$t$取0 s~5 s；$\mu$和$\sigma$分别为正态分布均值和标准差。图7为目标概率密度函数。

图  7  目标概率密度(精确解)

Figure  7.  Target probability density (exact solution)

下载: 全尺寸图片 幻灯片

图8为利用TVD差分法在时间步长为0.0001 s条件下计算的概率密度数值解。图8的Dirac函数型初值条件零时刻的概率分布较为尖锐，概率密度函数(Probability density function, PDF)峰值为12.85，而图7的精确解初始时刻PDF峰值为7.97。

图  8  时间步长0.0001 s的概率密度 (TVD差分数值解)

Figure  8.  Probability density with time step of 0.0001 s (TVD difference numerical solution)

下载: 全尺寸图片 幻灯片

选取原始的时间步长为${\rm{d}}t = 0.01\;{\rm{s}}$，根据式(27)和式(28)即可得到100条目标样本曲线。这100条随机样本的均值和标准差分别按传统数理统计方法和数值差分法计算，结果见图9。

图  9  与精确解的结果对比

Figure  9.  The results are compared with the exact solution

下载: 全尺寸图片 幻灯片

图9(a)中，${\rm{d}}t = 0.01\;{\rm{s}}$的时间步长能够满足构造样本精度要求，而对于${\rm{d}}Z \geqslant 1.0075$的CFL条件，过大的空间步长将导致无法进行差分计算。这进一步表明当结构响应一阶时间导数过大时，仅满足结构响应精度要求的时间步长并不能满足概率密度演化方程的差分求解精度。图9(b)中，初值条件在分布范围方向上的平滑性很差，这也导致图9(b)的标准差结果在初始时刻大幅震荡，进而导致之后0 s~2 s内的标准差都严重偏离精确解；数值差分标准差曲线后半段的离散性逐渐增大是因为通量限制器的存在导致概率密度分布范围只能增大不能减小引起的。

图10正态分布型初值条件标准差$\sigma = {\rm{d}}Z$时的概率密度分布结果。由于采用了正态分布型初值条件，其初始时刻PDF峰值为11.78，与图8的Dirac函数型初值条件相比，PDF峰值降低，分布范围方向上的可导性提高，使概率密度分布结果更接近图7的精确解。

图  10  $\sigma = {\rm{d}}Z$时的概率密度

Figure  10.  The probability density at $\sigma = {\rm{d}}Z$

下载: 全尺寸图片 幻灯片

以差分解计算误差的时间平均值${E_{{\rm{rro}}}}$作为计算精度指标：

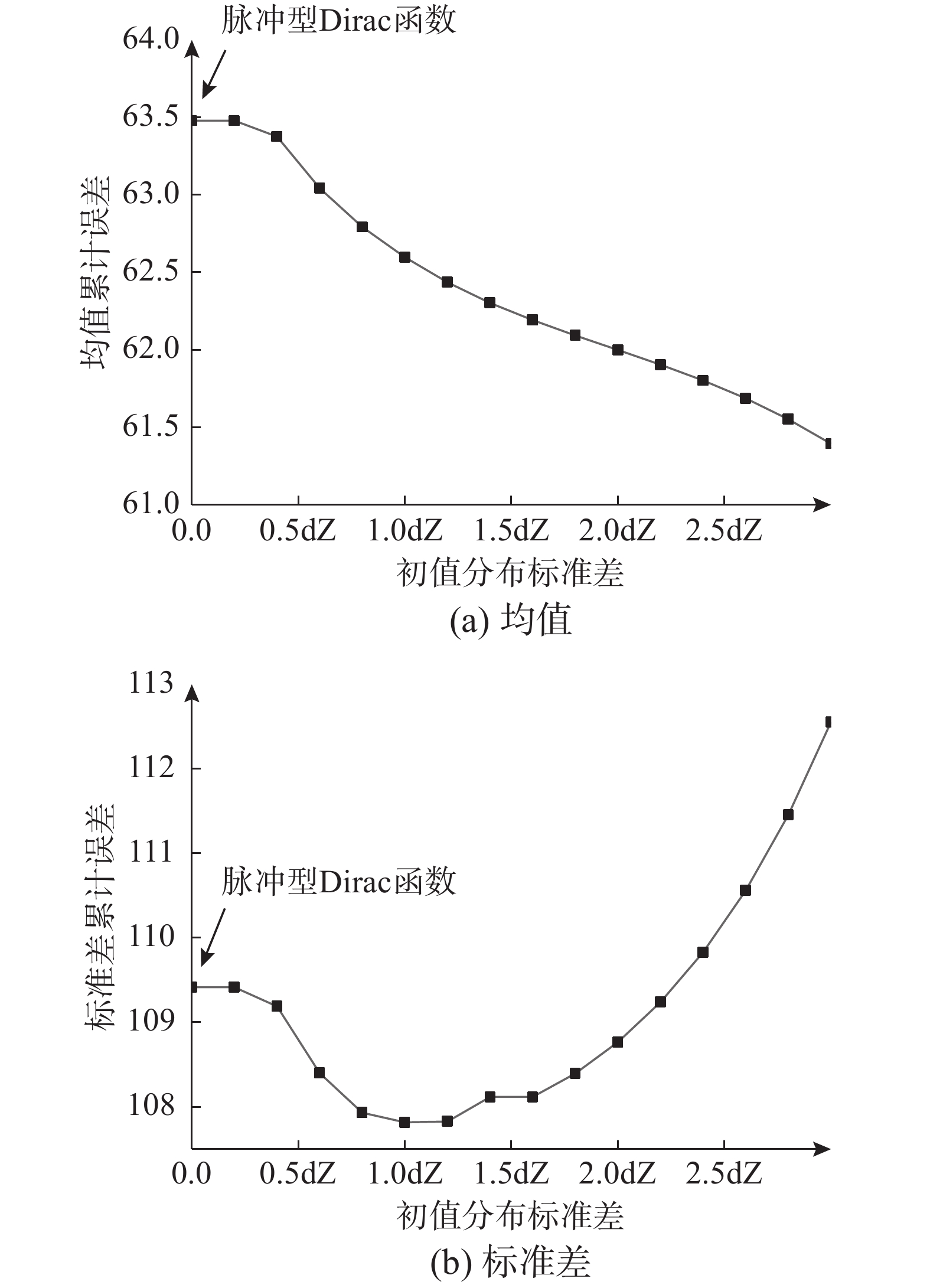
式中，${E_i}$为第$i$时间点均值或标准差的误差。

使用不同$\sigma$值($\sigma$以0.2${\rm{d}}Z$为间隔)的正态分布型初值条件开展数值计算，结果见图11。图11结果表明：改进的正态分布型初值条件可通过调节标准差$\sigma$达到减小均值和标准差计算误差的目的。随着$\sigma$的增大，均值累计误差一直减小；而标准差累计误差先减小后增大，$\sigma = {\rm{d}}Z$时达到最小值。与式(27)精确解的初始概率相比，按式(3)Dirac函数型初值条件累加求和得到的初始概率分布更集中(即峰值更大，分布范围更窄)，因此，正态分布型初值条件在$\sigma = {\rm{d}}Z$之前，$\sigma$的增大导致初始概率分布的峰值逐渐降低，分布范围逐渐变宽，初始概率分布向精确解逼近；随着$\sigma$的进一步增大，虽然初始概率分布的峰值依旧向精确解靠近，但分布范围却比精确解更大，导致标准差累计误差不再减小。

图  11  初值条件对累计误差的影响

Figure  11.  Influence of initial condition on cumulative error

下载: 全尺寸图片 幻灯片

4   结论

本文分析了单边差分、L-W双边差分和TVD差分三种差分方法在不同差分时间步长条件下的样本离散性，指出了差分精度的影响因素，提出了TVD差分法的时间步长合理选取方法和正态分布型初值条件，通过数值算例验证了时间步长选取方法和正态分布型初值条件的准确性及普适性，并得到如下结论：

(1) L-W双边差分法的单样本概率演化离散性最小，误差允许范围内可采用的时间步长最大，当计算结果仅关注均值和标准差等统计指标，而不考虑概率密度分布情况时，建议使用L-W双边差分法开展高效的数值求解。

(2) 通过对比三种差分方法的数值耗散情况，得到数值差分计算精度的影响因素包括：结构响应方向上各时刻概率密度函数的可导性、结构响应一阶时间导数、差分求解次数 (或时间长度)和概率初值条件。

(3) 基于TVD差分开展PDEE数值求解时，空间离散步长不仅要满足CFL条件要求，还应满足各样本差异性的最大值限制，本文提出的差分时间步长选取方法有效降低了TVD差分的单样本离散性和多样本概率密度求和导致的累加误差，并且差分时间步长可根据样本差异程度灵活调整。

(4) 在传统的脉冲函数型初值条件基础上提出了一种更平滑且可以通过标准差$\sigma$控制的正态分布型初值条件形式。当$\sigma$取值较小时，该分布条件近似于脉冲型Dirac函数初值分布。合适的标准差$\sigma$可以提高正态分布型初值条件的数值差分精度。