基础竖向多频参数激励下圆弧拱平面内动力失稳研究

钟子林; 刘爱荣

doi:10.6052/j.issn.1000-4750.2021.07.ST06

基础竖向多频参数激励下圆弧拱平面内动力失稳研究

钟子林^{1, 2,},
刘爱荣^1, ,

1.
广州大学风工程与工程振动研究中心，广东，广州 510006
2.
广州铁路职业技术学院，广东，广州 510430

基金项目: 国家自然科学基金项目(51878188)；111计划项目(21021)；广州市科技计划项目(20212200004)

详细信息

作者简介:
钟子林(1990−)，男，广东人，博士，主要从事新型拱桥的动力稳定性研究(E-mail: zl.zhong@e.gzhu.edu.cn)

通讯作者:
刘爱荣(1972−)，女，山西吕梁人，教授，博士，主要从事新型拱桥的静动力稳定性研究 (E-mail: liuar@gzhu.edu.cn)

中图分类号: TU311.2
计量
- 文章访问数: 797
- HTML全文浏览量: 403
- PDF下载量: 89
出版历程
- 收稿日期: 2021-07-20
- 修回日期: 2021-08-22
- 录用日期: 2021-11-01
- 网络出版日期: 2021-11-10
- 刊出日期: 2022-03-24

STUDIES ON IN-PLANE DYNAMIC INSTABILITY OF VERTICALLY AND PARAMETRICALLY BASE MULTI-FREQUENCY EXCITED CIRCULAR ARCHES

ZHONG Zi-lin^{1, 2,},
LIU Ai-rong^1, ,

1.
Research Centre for Wind Engineering and Engineering Vibration, Guangzhou University, Guangzhou, Guangdong 510006, China
2.
Guangzhou Railway Polytechnic, Guangzhou, Guangdong 510430, China

摘要

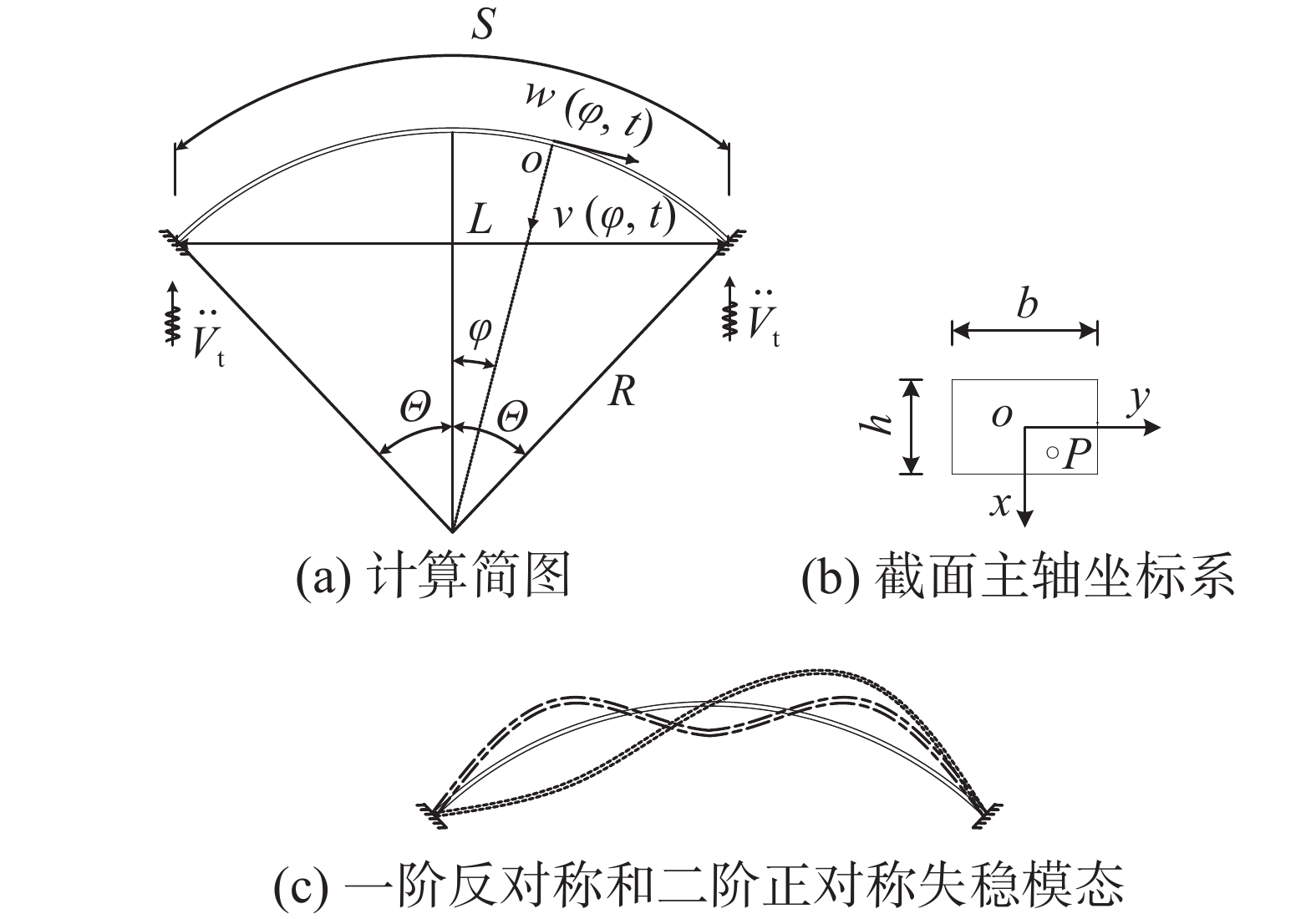
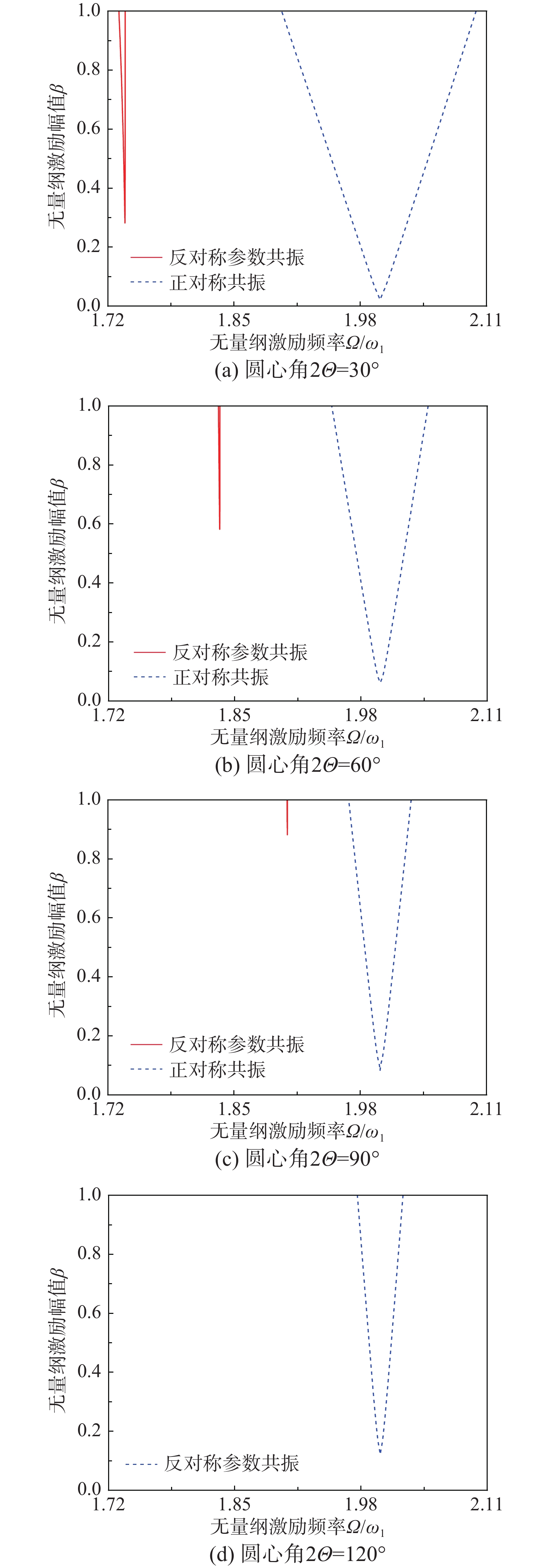
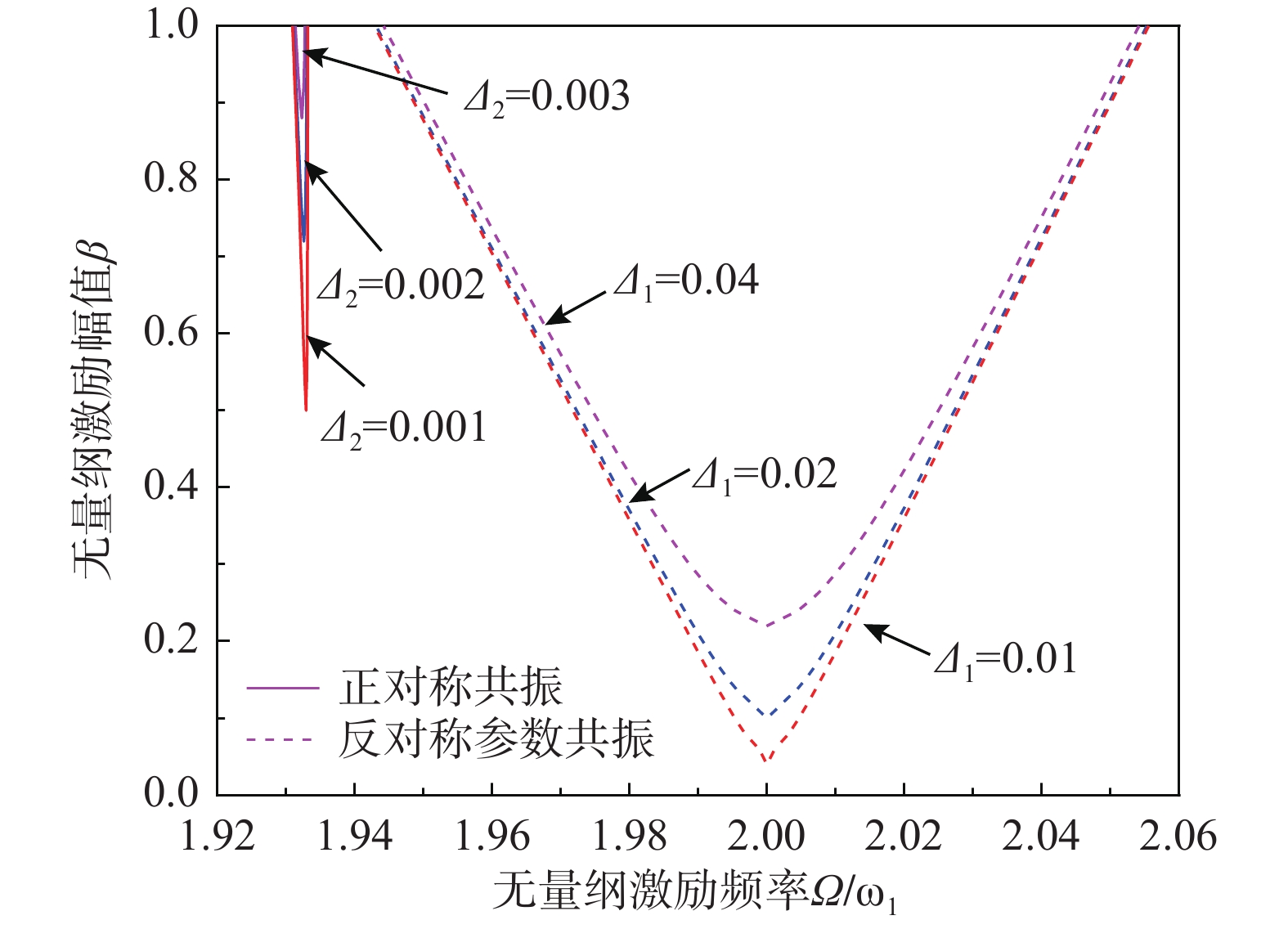
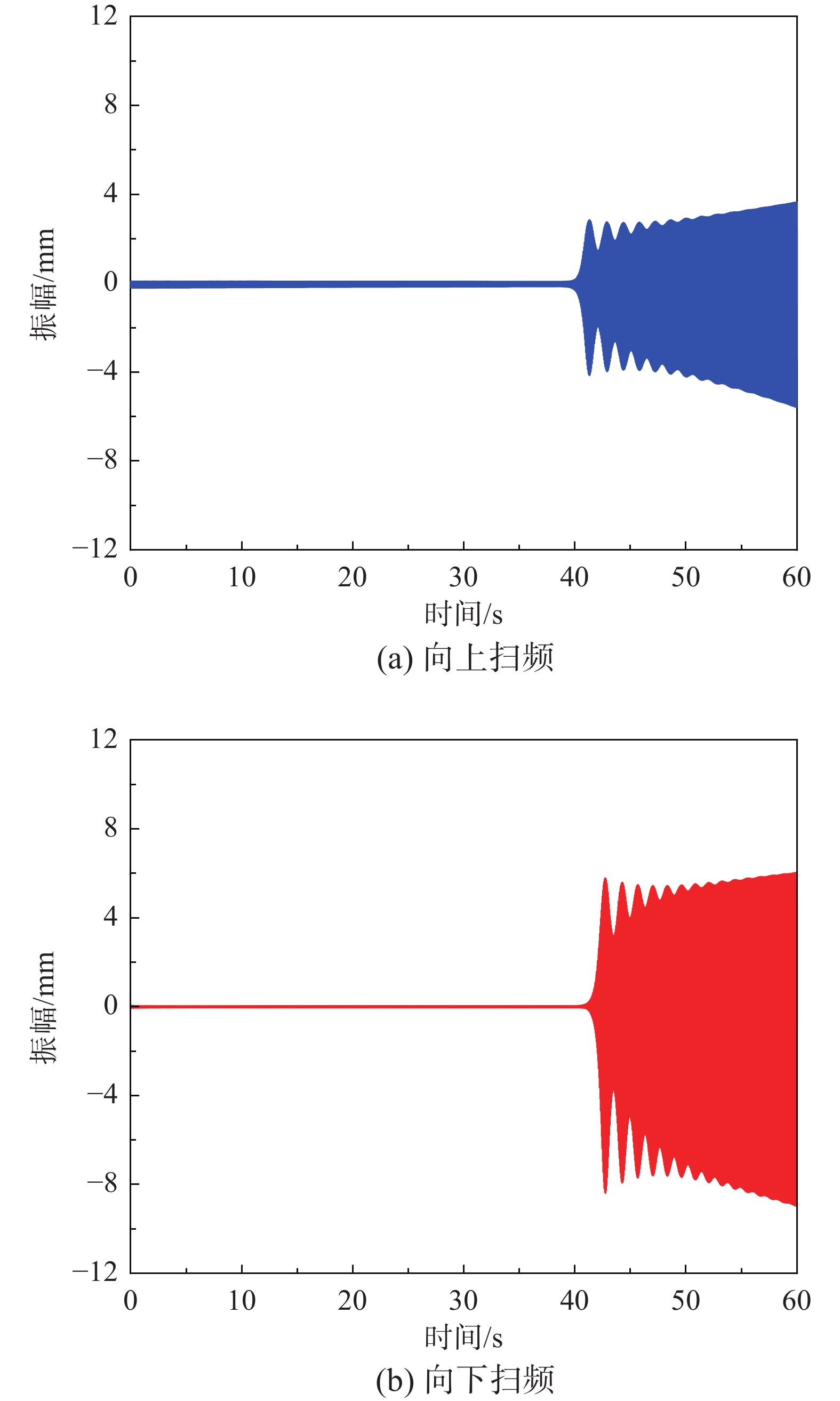
摘要: 地震波、冲击波、环境振动激励会通过地基基础传递到拱上，致使拱发生动力失稳失去承载能力。为深入研究拱在基础竖向激励下的动力稳定性，该文基于能量法，建立了基础竖向激励下圆弧拱平面内动力稳定能量方程，利用哈密顿原理得到了拱面内径向和切向振动的耦合控制方程，求解了圆弧拱平面内失稳前的动轴力与动弯矩解析解。引入拱轴线不可压缩假设，解决了圆弧拱平面内动力控制方程的解耦问题。利用伽辽金法建立了基础竖向多频激励下圆弧拱平面内二阶常微分动力稳定方程，运用多尺度法推导了基础竖向多频激励下圆弧拱平面内动力失稳的临界激励频率解析公式，得到了圆弧拱同时发生一阶反对称参数共振和二阶正对称共振失稳的动力不稳定域，并利用有限元数值分析验证了理论解析解的正确性。进一步分析了拱矢跨比、长细比和圆心角对动力不稳定域的影响。
- 圆弧拱 /
- 基础竖向多频激励 /
- 平面内失稳 /
- 多尺度法 /
- 动力不稳定域
Abstract: Seismic wave, shock wave and the ambient vibration excitation may be transmitted to an arch through the base, resulting in the dynamic instability and the loss of bearing capacity of the arch. In order to deeply study the dynamic stability of the arch under a vertical base excitation, the energy equations of the in-plane dynamic stability of the circular arch under a vertical base excitation are established based on the energy method. The coupled governing equations of the in-plane radial and tangential vibration of the investigated arch are obtained by using Hamilton principle. The analytical solutions of the dynamic axial forces and the dynamic bending moments prior to the in-plane dynamic instability are solved. For decoupling the in-plane dynamic governing equation, it is assumed that the arch is incompressible. Using the Galerkin method, the in-plane second-order ordinary differential dynamic stability equations of the circular arch under a vertical base multi-frequency excitation are established. The analytical equations of critical excitation frequencies of the circular arch under a vertical base multi-frequency excitation are derived via the multi-scale method, and the dynamic instability regions for the simultaneous first-order antisymmetric parametric resonance and second-order symmetric resonance instability of the circular arch verified by FEA are determined accordingly. Furthermore, the influences of span ratio, slenderness ratio and central angle on the dynamic instability region are analyzed.
- circular arches /
- base vertical multi-frequency excitation /
- in-pane instability /
- multi-scale method /
- dynamic instability region

HTML全文

结构分析往往采用数值模型来分析和预测结构响应。但是由于不确定性的存在，数值模型的结构响应预测值和实际测量值之间不可避免地存在差异^[1-3]。针对此问题，近年有很多学者采用模型修正技术来确定结构系统的最可信结构模型，实现对结构的参数识别和后续的损伤诊断^[4-10]。

贝叶斯模型修正方法是一种随机模型修正方法，能够很好地量化不确定性^[11]。在贝叶斯修正框架中，待修正物理参数的后验分布表示为先验分布和似然函数的乘积。然而，对于一些复杂结构，由于物理参数和结构测量输出变量(下文中也称为“结构特征”)之间的关系通常不是显式的^[12]，似然函数很难直接得到，这也造成了贝叶斯模型修正的计算成本往往变得难以承受。因此，某些代理模型，如Kriging法^[13]和多项式混沌展开^[14-15]已被应用于模型修正，作为非常复杂的数值模型的替代。

尽管贝叶斯模型修正方法量化了修正结果的不确定性，但所获得的不确定性对结构的复杂性很敏感，这主要体现在参数维数和结构非线性关系上。在这种复杂模型的存在下，修正结果往往是不理想的。模型的高维度和非线性不仅给贝叶斯模型修正过程带来了很大的挑战，而且也为代理模型的应用带来挑战。因此，确定贝叶斯模型修正方法和代理模型在这些复杂情况下的适用性是有意义的。

本文将贝叶斯模型修正框架应用于十层框架和国家体育场模型两个不同复杂程度的结构实例。这两个模型分别代表高维线性模型和小样本下非线性模型。通过实例分析，本文探讨了Kriging模型和多项式混沌展开(PCE)两种代理模型的优、缺点。研究结果为复杂结构模型修正中代理模型的选择提供了参考。此外，为了提高代理模型的性能，本文还提出来一种适用于代理模型的集成学习框架，用以提升模型修正的精度与鲁棒性。

1 研究方法

1.1 贝叶斯模型修正理论

贝叶斯模型修正方法建立在贝叶斯公式的基础上，参数θ的后验分布p(θ|D, M)可表示为：

$p(\theta \left| {D,M} \right.) = \frac{{p(D\left| {\theta ,M} \right.)p(\theta \left| M \right.)}}{{p(D\left| M \right.)}}$

(1)

式中：p(θ|M)为先验分布，表示基于经验和历史数据得到的修正参数的先验知识；p(D|M)为归一化常数；p(D|θ,M)为似然函数，反映在给定参数情况下得到测量值的条件概率。对于服从正态分布的正态参数，似然函数可表示为：

$p(D|\theta ,M) = \exp \left( - \frac{{{J_g}(\theta )}}{{2\sigma _\varepsilon ^2}}\right)$

(2)

式中： $\sigma _\varepsilon ^2$ 为预测误差的度量； ${J_g}(\theta )$ 为拟合优度函数，可表示为：

${J_g}(\theta ) = \sum\limits_{i = 1}^m {\frac{{{{\hat \Omega }^{(i)}}^2 - {\Omega ^{(i)}}{{(\theta )}^2}}}{{{{\hat \Omega }^{(i)}}^2}}}$

(3)

式中： ${\hat \Omega }^{(i)}$ 和 ${ \Omega }^{(i)}$ (θ)为测量特征与模型预测特征；m为参数维数。

后验分布的计算涉及复杂的高维积分，通常难以直接得到，本文使用过渡马尔科夫链蒙特卡洛采样(TMCMC)方法，构造一系列收敛到后验分布的中间分布来完成采样。待修正物理参数与模型预测特征之间的关系通过Kriging和PCE两种代理模型得到。

1.2 集成学习框架

为减少Kriging模型和PCE模型的泛化误差，结合Bootstrap Aggregating (Bagging)和Adaptive Boosting (Adaboost)两种集成学习技术建立了适用于代理模型的集成学习框架，算法总结如下：

1) 选择包括m个点的训练集D，初始化样本权重 ${w_{0,i}}{\text{ = }}{1/ m}$ 。确定需要集成的代理模型个数p。对于j=1, 2,···, p重复步骤2~4；

2) 使用自助采样法生成n个训练子集，并训练n个代理模型 $S_1^{(j)},S_2^{(j)},\cdots,S_n^{(j)}$ ，其均值作为新的代理模型 ${S^{(j)}}$ ；

3) 计算模型预测值相对于真实值的误差 ${e_{j,i}}$ (i=1, 2,···, nm)和模型权重：

${a_j} = \frac{1}{2}\ln \frac{{1 - \displaystyle\sum\nolimits_1^{nm} {{e_{j,i}}/nm} }}{{\displaystyle\sum\nolimits_1^{nm} {{e_{j,i}}/nm} }}$

(4)

4) 更新样本权重：

${w_{j,i}} = \frac{{{w_{j - 1,i}}}}{{{Z_j}}}a_j^{1 - {e_{j,i}}}$

(5)

5) 最终模型为 $\displaystyle\sum\nolimits_{j = 1}^p {{a_j}{S^{(j)}}}$ 。

2 算例

2.1 十层框架结构

考虑十层框架，楼层质量初始值m=11170 kg，楼层刚度初始值K₀=46.08 MN/m。选取待修正参数为各层的无量纲抗侧刚度，定义为修正后的楼层刚度与初始楼层刚度之比(θ_i=K_i/K₀, i=1, 2, ···, 10)。参数的具体信息见表1。在该算例的模型修正中，采用了2种代理模型和1种解析模型，并对修正结果进行了比较。本例同时研究探讨了小样本下的模型修正，代理模型的训练样本空间采用概率配点法和稀疏网格积分方法进行配置，10个参数所对应的训练点数目是21。在本例中，与被测特征对应的不确定参数值有多个组合(此时参数是局部可识别的)。在这种高维情况下，后验分布难以可视化，因此采用K-means聚类分析来消除局部最优解。聚类前、后的参数修正值见表2。聚类前，解析模型和PCE模型的修正结果存在一定误差；聚类后，误差均降低到10%以下，表明聚类显著提高了代理模型的预测精度。聚类前的频率修正结果见表3。可以看到，误差都在5%以内。图1反映了不同方法中有代表性的部分结构特征的修正值。Kriging模型在初始步骤中比其他方法波动更容易受到影响。但这三种方法均收敛得很快，且几乎在相同的迭代步骤收敛。这意味着无论采用哪种方法，收敛速度都是可以接受的。

表 1 十层框架中待修正参数的描述

Table 1. Description of updated parameters in ten-storey frame

参数	真实值	变异系数	先验分布	区间
θ₁	1.5	0.01	均匀分布	[0,3]
θ₂~θ₉	1.0	0.01	均匀分布	[0,3]

下载: 导出CSV

| 显示表格

表 2 十层框架的待修正参数(括号内为误差百分比)

Table 2. Updated parameters in ten-storey frame (% errors in parenthesis)

参数	聚类前			聚类后
参数	解析法	Kriging法	PCE法	解析法	Kriging法	PCE法
θ₁	1.92 (28.0)	1.68 (12.8)	1.97 (38.1)	1.60 (6.5)	1.48 (2.5)	1.55 (3.4)
θ₂	1.15 (15.0)	0.96 (−3.7)	1.09 (8.6)	0.94 (−5.5)	0.93 (6.6)	1.07 (6.8)
θ₃	1.02 (1.9)	1.00 (0.1)	0.97 (−2.6)	1.12 (11.7)	0.98 (2.1)	0.91 (−8.8)
θ₄	0.90 (−10.1)	1.01 (0.7)	1.06 (−5.9)	0.93 (−6.7)	1.05 (4.3)	0.97 (−3.2)
θ₅	1.04 (3.6)	1.05 (4.7)	1.06 (6.4)	1.01 (1.0)	1.04 (4.4)	0.97 (−2.7)
θ₆	1.00 (0.2)	1.06 (6.1)	1.15 (15.4)	0.99 (−0.8)	1.01 (1.1)	0.89 (−9.6)
θ₇	0.98 (−2.4)	1.02 (2.7)	1.11 (10.5)	0.99 (−0.8)	1.03 (2.6)	0.93 (−6.8)
θ₈	1.03 (3.2)	1.06 (5.9)	1.22 (22.5)	0.94 (−6.4)	1.04 (3.8)	0.90 (−9.7)
θ₉	1.00 (−0.3)	1.06 (6.2)	1.03 (3.0)	0.91 (−9.2)	1.08 (7.6)	1.06 (5.7)
θ₁₀	0.96 (−3.8)	1.24 (23.5)	1.25 (24.5)	0.96 (−3.5)	1.07 (6.6)	1.11 (10.7)

下载: 导出CSV

| 显示表格

表 3 十层框架中的特征修正结果

Table 3. Updated features in ten-storey frame

参数	实测值	解析模型		Kriging模型		PCE模型
参数	实测值	修正值	误差/(%)	修正值	误差/(%)	修正值	误差/(%)
f₁	1.58	1.57	−0.2	1.60	0.4	1.59	0.2
f₂	4.70	4.69	−0.1	4.85	3.3	4.73	0.7
f₃	7.71	7.78	1.1	7.72	0.2	7.84	1.9
f₄	10.51	10.57	0.6	10.67	1.5	10.76	2.3
f₅	13.08	13.40	2.5	13.35	2.2	13.36	2.2
f₆	15.31	15.72	2.7	16.07	5.0	15.75	3.0
f₇	17.16	17.23	0.3	17.70	3.1	17.71	3.2
f₈	18.62	18.92	1.6	19.25	3.5	19.14	2.8
f₉	19.65	19.76	0.6	20.44	4.0	20.30	3.3
f₁₀	20.24	20.11	−0.7	20.69	2.1	20.40	1.3

下载: 导出CSV

| 显示表格

同时将1.2节中提出的集成学习框架应用于该十层框架，代理集成模型和单一代理模型修正结果的比较在表4给出。PCE模型和Kriging模型的权重为 ${a_{\rm P}}{\text{ = }}0.3673,$ ${a_{\rm K}}{\text{ = }}0.6327$ 。模型权重也表明了Kriging模型比PCE模型更适用于线性高维情形。

图 1 不同方法下结构特征的对比

Figure 1. Comparison of features in different methods

下载: 全尺寸图片幻灯片

表 4 十层框架中集成前后的修正参数(括号内为误差百分比)

Table 4. Updated parameters before and after ensemble in ten-storey frame (% errors in parenthesis)

待修正参数	Kriging模型	PCE模型	集成模型
θ₁	1.68 (12.8)	1.97 (38.1)	1.55 (3.4)
θ₂	0.96 (−3.7)	1.09 (8.6)	1.07 (6.8)
θ₃	1.00 (0.1)	0.97 (−2.6)	0.91 (−8.8)
θ₄	1.01 (0.7)	1.06 (−5.9)	0.97 (−3.2)
θ₅	1.05 (4.7)	1.06 (6.4)	0.97 (−2.7)
θ₆	1.06 (6.1)	1.15 (15.4)	0.89 (−9.6)
θ₇	1.02 (2.7)	1.11 (10.5)	0.93 (−6.8)
θ₈	1.06 (5.9)	1.22 (22.5)	0.90 (−9.7)
θ₉	1.06 (6.2)	1.03 (3.0)	1.06 (5.7)
θ₁₀	1.24 (23.5)	1.25 (24.5)	1.07 (6.8)

下载: 导出CSV

| 显示表格

2.2 国家体育场

分析非线性结构国家体育场，有限元模型如图2所示。待修正参数为钢材弹性模量的修正值与初始值之比。考虑小样本情形，代理模型的样本空间采用概率配点法和稀疏网格积分方法进行配置。训练点数量为5。此时先验分布对结果影响很大，故本例对先验分布的均值取5个不同的值来研究小样本情况下先验分布对后验分布的影响。表5给出了参数的详细信息。结构特征选为前五阶模态频率。

图 2 国家体育场有限元模型

Figure 2. Finite element model of the National Stadium

下载: 全尺寸图片幻灯片

表 5 鸟巢中待修正参数的描述

Table 5. Description of updated parameters in the National Stadium

参数	先验分布	区间	备注	真实值
θ₁	均匀分布	[μ−0.5, μ+0.5]	μ ϵ {1.05, 1.30, 1.50, 1.75, 2.00}	1.75
θ₂	均匀分布	[μ−0.5, μ+0.5]	μ ϵ {1.05, 1.30, 1.50, 1.75, 2.00}	1.75

下载: 导出CSV

| 显示表格

由表6可知，θ的先验均值对修正精度有明显影响。表7给出了先验均值等于真实值时参数和频率的修正结果。同时可以看出，频率的预测精度高于参数的预测精度。另外，PCE模型对待修正参数和结构特征的修正结果优于Kriging模型。PCE模型的另一个优点是，迭代步骤几乎只有Kriging模型的1/2，这说明PCE模型比Kriging模型更适用于低维小样本情况。表8同时给出了1.2节中提出的代理集成模型的修正结果，代理集成模型在不降低时间复杂度的情况下有效改善了修正精度。在此算例中，PCE模型和Kriging模型的模型权重分别为 ${a_{\rm P}}{\text{ = }}0.4288,$ ${a_{\rm K}}{\text{ = }}0.5712$ 。模型权重也表明了PCE模型比Kriging模型更适用于非线性低维情形。

表 6 鸟巢中待修正参数(括号内为误差百分比)

Table 6. Updated parameters in the National Stadium (% errors in parenthesis)

先验均值μ	1.05		1.30		1.50		1.75		2.00
参数	θ₁	θ₂	θ₁	θ₂	θ₁	θ₂	θ₁	θ₂	θ₁	θ₂
Kriging模型	1.89 (8.0)	1.80 (2.8)	1.85 (5.6)	1.83 (4.5)	1.85 (5.6)	1.81 (3.4)	1.83 (4.5)	1.82 (4.0)	1.93 (11.2)	1.94 (10.9)
PCE模型	1.87 (6.8)	1.70 (−3.1)	1.82 (4.1)	1.67 (−4.6)	1.85 (5.7)	1.66 (−5.1)	1.72 (−1.5)	1.74 (−0.6)	1.94 (11.3)	1.72 (−1.6)

下载: 导出CSV

| 显示表格

表 7 鸟巢中特征修正结果(括号内为误差百分比)

Table 7. Updated features in the National Stadium (% errors in parenthesis)

变量	初始值	Kriging模型	PCE模型	集成模型
f₁/Hz	1.118	1.109 (−0.81)	1.113 (−0.45)	1.114 (−0.37)
f₂/Hz	1.133	1.129 (−0.48)	1.128 (−0.44)	1.129 (−0.35)
f₃/Hz	1.270	1.271 (0.06)	1.265 (−0.37)	1.272 (−0.16)
f₄/Hz	1.838	1.823 (−0.81)	1.830 (−0.44)	1.829 (−0.49)
f₅/Hz	1.964	1.948 (−0.79)	1.956 (−0.43)	1.962 (−0.10)

下载: 导出CSV

| 显示表格

表 8 鸟巢中集成前后的修正参数(括号内为误差百分比)

Table 8. Updated parameters before and after ensemble in the National Stadium (% errors in parenthesis)

变量	Kriging模型	PCE模型	集成模型
θ₁	1.83 (4.5)	1.72 (−1.5)	1.75 (0.4)
θ₂	1.82 (4.0)	1.74 (−0.6)	1.74 (−0.6)

下载: 导出CSV

| 显示表格

3 结论

本文结合过渡马尔科夫链蒙特卡罗(TMCMC)算法和K-means聚类分析提出了一种贝叶斯结构模型修正框架。通过2个不同结构复杂度的算例验证了该方法的有效性。在这3个例子中，对Kriging模型和PCE模型进行了研究和比较，显示了他们的优点和局限性。得到的结论如下：

(1) 对于高维线性情形下的10层框架，解析方法和两种代理模型均适用，Kriging模型的精度优于PCE模型。对于高维非线性情形的国家体育场，PCE模型的精度高于Kriging模型。

(2) 为了提高代理模型在模型修正中表现，结合Bagging和Adaboost，提出了一种适用于代理模型的集成学习算法。结果表明，该集成学习方法提升了代理模型的精度与鲁棒性，同时可以减少计算工作量。

图 1 基础竖向激励下圆弧拱动力系统

Figure 1. Dynamic system of the circular arch under a vertical base excitation

下载: 全尺寸图片幻灯片

图 2 基础激励下不同矢跨比圆弧拱平面内动力失稳的动力不稳定域

Figure 2. Dynamic instability regions of the circular arch under a base excitation for different span-rise ratio

下载: 全尺寸图片幻灯片

图 3 基础激励下不同长细比圆弧拱平面内动力失稳的动力不稳定域

Figure 3. Dynamic instability regions of the circular arch under a base excitation for different slenderness ratio

下载: 全尺寸图片幻灯片

图 4 基础激励下不同圆心角圆弧拱平面内参数动力失稳的动力不稳定域

Figure 4. Dynamic instability regions of the circular arch under a base excitation for different central angle

下载: 全尺寸图片幻灯片

图 5 不同阻尼衰减率下圆弧拱平面内参数动力失稳的动力不稳定域

Figure 5. Dynamic instability regions of the circular arch for different damping decrement

下载: 全尺寸图片幻灯片

图 6 基础双余弦激励下圆弧拱平面内参数动力失稳的振幅时程( β=1)

Figure 6. Amplitude of the circular arch under double cosine base excitation for the in-plane parametric resonance

下载: 全尺寸图片幻灯片

表 1 基础双余弦激励下圆弧拱平面内一阶反对称参数共振失稳临界激励频率的解析解与数值解(f/L=1/10)

Table 1 Analytical and numerical solutions of the critical excitation frequencies of first-order antisymmetric parametric resonance instability of a circular arch plane under a base double cosine excitations

无量纲激励幅值β	临界激励频率下限值 Ω_L/Hz			临界激励频率上限值 Ω_H/Hz
无量纲激励幅值β	数值解	解析解	误差 /(%)	数值解	解析解	误差 /(%)
1	37.63	37.38	0.66	42.94	43.00	0.14
0.9	37.95	37.68	0.71	42.66	42.74	0.19
0.8	38.27	37.98	0.76	42.38	42.47	0.21
0.7	38.59	38.28	0.80	42.09	42.21	0.29
0.6	38.90	38.57	0.85	41.80	41.94	0.33
0.5	39.21	38.87	0.87	41.52	41.66	0.34
0.4	39.52	39.16	0.91	41.23	41.39	0.39

下载: 导出CSV

参考文献(22)

[1]	Bolotin V V. The dynamic stability of elastic systems [M]. San Francisco: Holden-Day, 1964.
[2]	Sophianopoulos D S, Michaltsos G T. Analytical treatment of in-plane parametrically excited undamped vibrations of simply supported parabolic arches [J]. Journal of Vibration & Acoustics, 2003, 125(1): 73 − 79.
[3]	王连华, 易壮鹏, 张辉. 周期荷载作用下几何缺陷拱的动力稳定性[J]. 湖南大学学报(自然科学版), 2007, 34: 16 − 19. Wang Lianhua, Yi Zhuangpeng, Zhang Hui. Dynamic stability of arch with the geometrical imperfection subject to the periodic load [J]. Journal of Hunan University (Natural Sciences), 2007, 34: 16 − 19. (in Chinese)
[4]	赵洪金, 刘超, 孟昭博, 吴敏哲. 周期径向荷载作用下圆弧格构拱动力稳定性分析[J]. 地震工程与工程振动, 2011, 31(6): 73 − 77. Zhao Hongjin, Liu Chao, Meng Zhaobo, Wu Minzhe. Analysis of dynamic stability of circular lattice arch subjected to periodic radial load [J]. Journal of Earthquake Engineering and Engineering Vibration, 2011, 31(6): 73 − 77. (in Chinese)
[5]	赵洪金, 刘超, 董宁娟, 吴敏哲. 考虑剪切变形的圆弧深拱参数共振稳定性分析[J]. 振动与冲击, 2012, 31(2): 119 − 122. doi: 10.3969/j.issn.1000-3835.2012.02.024 Zhao Hongjin, Liu Chao, Dong Ningjuan, Wu Minzhe. Stability analysis for parametric resonance of a circular deep arch considering influence of shear deformation [J]. Journal of Vibration and Shock, 2012, 31(2): 119 − 122. (in Chinese) doi: 10.3969/j.issn.1000-3835.2012.02.024
[6]	董宁娟, 赵洪金. 开口薄壁截面圆弧拱空间动力稳定性分析[J]. 科学技术与工程, 2012, 12(32): 8569 − 8573. doi: 10.3969/j.issn.1671-1815.2012.32.018 Dong Ningjuan, Zhao Hongjin. Analysis of spatial dynamic stability for thin-walled circular arches with open-section [J]. Science Technology and Engineering, 2012, 12(32): 8569 − 8573. (in Chinese) doi: 10.3969/j.issn.1671-1815.2012.32.018
[7]	董宁娟, 赵洪金. 闭口薄壁截面圆弧拱空间动力稳定性分析[J]. 噪声与振动控制, 2013(2): 23 − 26. Dong Ningjuan, Zhao Hongjin. Analysis of spatial parametric resonance for thin-walled circular arches with closed section [J]. Noise and Vibration Control, 2013(2): 23 − 26. (in Chinese)
[8]	刘爱荣, 李晶, 黄永辉. 拱的静动力稳定性研究进展[J]. 广州大学学报(自然科学版), 2016, 15(5): 1 − 12. Liu Airong, Li Jing, Huang Yonghui. Research progress on static and dynamic stability of arches [J]. Journal of Guangzhou University( Natural Science Edition), 2016, 15(5): 1 − 12. (in Chinese)
[9]	Liu A R, Yang Z C, Lu H W, Pi Y L. Experimental and analytical investigation on the in-plane dynamic instability of arches owing to parametric resonance [J]. Journal of Vibration and Control, 2018, 24(19): 4419 − 4432. doi: 10.1177/1077546317726210
[10]	Liu A R, Lu H W, Fu J Y, Pi Y L, Huang Y Q, Li J, Ma Y W. Analytical and experimental studies on out-of-plane dynamic instability of shallow circular arch based on parametric resonance [J]. Nonlinear Dynamics, 2017, 87(1): 677 − 694. doi: 10.1007/s11071-016-3068-7
[11]	Zhong Z L, Liu A, Pi Y L, Deng J, Fu J Y, Gao W. In-plane dynamic instability of a shallow circular arch under a vertical-periodic uniformly distributed load along the arch axis [J]. International Journal of Mechanical Sciences, 2021, 189: 105973. doi: 10.1016/j.ijmecsci.2020.105973
[12]	Liu A, Yang Z, Bradford M A, Pi Y L. Nonlinear dynamic buckling of fixed shallow arches under an arbitrary step radial point load [J]. Journal of Engineering Mechanics, 2018, 144(4): 04018012. doi: 10.1061/(ASCE)EM.1943-7889.0001425
[13]	Yang Z C, Liu A R, Yang J, Fu J Y, Yang B. Dynamic buckling of functionally graded graphene nanoplatelets reinforced composite shallow arches under a step central point load [J]. Journal of Sound and Vibration, 2020, 465: 115019. doi: 10.1016/j.jsv.2019.115019
[14]	Yang Z C, Liu A R, Pi Y L, et al. Nonlinear dynamic buckling of fixed shallow arches under impact loading: An analytical and experimental study [J]. Journal of Sound and Vibration, 2020, 487: 115622. doi: 10.1016/j.jsv.2020.115622
[15]	Chen J S, Yang C H. Experiment and theory on the nonlinear vibration of a shallow arch under harmonic excitation at the end [J]. Journal of Applied Mechanics, 2007, 24(6): 1061 − 1070.
[16]	Zhong Z, Liu A, Fu J, et al. Analytical and experimental studies on out-of-plane dynamic parametric instability of a circular arch under a vertical harmonic base excitation [J]. Journal of Sound and Vibration, 2021, 500: 116011. doi: 10.1016/j.jsv.2021.116011
[17]	Pi Y L, Bradford M A, Uy B. In-plane stability of arches [J]. International Journal of Solids & Structures, 2002, 39(1): 105 − 125.
[18]	Pi Y L, Bradford M A, Guo Y L. Revisiting nonlinear in-plane elastic buckling and postbuckling analysis of shallow circular arches under a central concentrated load [J]. Journal of Engineering Mechanics, 2016, 142(8): 04016046. doi: 10.1061/(ASCE)EM.1943-7889.0001098
[19]	Henrych J. Dynamics of arches and frames [M]. New York: Elsevier, 1981.
[20]	Chen H L, Jin F N, Fan H L. Elastic responses of underground circular arches considering dynamic soil-structure interaction: a theoretical analysis [J]. Acta Mechanica Sinica, 2003, 29(1): 110 − 122.
[21]	Chen H L, Xia Z C, Zhou J N, Fan H L, Jin F N. Dynamic responses of underground arch structures subjected to conventional blast loads: Curvature effects [J]. Archives of Civil and Mechanical Engineering, 2013, 13(3): 322 − 333. doi: 10.1016/j.acme.2013.04.004
[22]	Kevorkian J K, Cole J D. Multiple scale and singular perturbation methods [M]. Springer Science & Business Media, 2012.

施引文献(37)

期刊类型引用(15)

1.	吴志豪，张辰啸，贾冬云，王鸿宇，傅阳. 螺栓球节点对钢管杆件屈曲特征值的影响. 安徽工业大学学报(自然科学版). 2024(01): 74-80 . 百度学术
2.	张爱林，张雪峰，姜子钦，邱萍，刘学春. 外加盖板的T形板装配式网壳节点抗弯性能研究. 工业建筑. 2024(01): 68-75 . 百度学术
3.	马胜玲，张莉. 考虑强弱轴影响的矩形钢管网壳结构弹塑性稳定性分析. 结构工程师. 2024(02): 23-32 . 百度学术
4.	张爱林，冯欢，姜子钦，刘怡. 新型法兰连接模块化装配式网壳结构稳定承载力智能化预测. 工业建筑. 2024(08): 54-61 . 百度学术
5.	刘廷勇，张爱林，李久林. 全装配大跨度空间钢结构预应力-高强度螺栓连接节点性能研究. 工业建筑. 2024(08): 44-53 . 百度学术
6.	苏斌. 基于四点弯曲力学模型的半刚性节点弹性转动刚度研究. 北方建筑. 2024(05): 59-65 . 百度学术
7.	刘峰成，吕召能，王琨，居永军，贵季荣. 装配式单层空间网格结构法兰型节点抗弯性能. 扬州大学学报(自然科学版). 2024(06): 17-24 . 百度学术
8.	杜学波，王珏. 爆炸冲击载荷下大型空间网壳的动态响应数值研究. 山西建筑. 2023(08): 58-62+66 . 百度学术
9.	王建省，刘戈，张鹏宇，张钊巍. 开孔单层网壳结构的力学特性及稳定性（英文）. 吉首大学学报(自然科学版). 2023(05): 57-63 . 百度学术
10.	顾金超，杜文风，汤朋山，高博青，董石麟. 榫卯式空心球节点受力性能数值模拟分析. 建筑结构学报. 2023(S2): 199-208+303 . 百度学术
11.	张班，黄锋，刘星辰，屈苗迪，万国庆. 偏载作用下半刚性螺栓节点的修正计算方法. 科学技术与工程. 2022(18): 7981-7987 . 百度学术
12.	张晓磊，李会军，陈旭，朱志强，喻晓晨. 嵌入式毂节点刚度及其单层球面网壳承载力研究. 工程力学. 2022(09): 179-190 . 本站查看
13.	彭伟波，聂俊，李克郎，黄波，谢振清，蔡文侃. 大型飞机机身壁板复合材料成型模具刚度优化. 航空制造技术. 2022(19): 114-118 . 百度学术
14.	黄昨越，晏致涛，翟运琼. 新型铝合金板式节点力学性能研究. 四川建筑科学研究. 2021(02): 28-34 . 百度学术
15.	何小辉，温四清，王新，董卫国. 某锥形穹顶半刚接单层网壳分析与设计. 建筑结构. 2021(14): 45-50+68 . 百度学术

其他类型引用(22)

资源附件(0)

图(6) / 表(1)

计量

文章访问数: 797
HTML全文浏览量: 403
PDF下载量: 89
被引次数: 37

1 研究方法
1.1 贝叶斯模型修正理论
1.2 集成学习框架
2 算例
2.1 十层框架结构
2.2 国家体育场
3 结论

基础竖向多频参数激励下圆弧拱平面内动力失稳研究

作者简介: 钟子林(1990−)，男，广东人，博士，主要从事新型拱桥的动力稳定性研究(E-mail: zl.zhong@e.gzhu.edu.cn)

通讯作者: 刘爱荣(1972−)，女，山西吕梁人，教授，博士，主要从事新型拱桥的静动力稳定性研究 (E-mail: liuar@gzhu.edu.cn)

计量

出版历程